住房价格空间格局及其影响因素的多尺度效应——以福州中心城区为例

林 珍，王武林，龚 姣，林 彤

（1.福州大学 环境与安全工程学院，福州 350108；2.湖南师范大学 旅游学院，长沙 410081；3.上海理工大学 光电信息与计算机工程学院，上海 200093）

住房是民生之重，经济之要，住房与城市的经济、社会、文化与生态发展质量均存在不同程度的耦合协调关系（杜金莹 等，2022）。大城市住房价格在土地财政、城镇化、商品房市场化改革等因素刺激下持续升高，公共空间资源（郑思齐，2013）和住房供需两者的非平衡性（董冠鹏 等，2011）导致住房价格空间差异显著。住房价格受城市结构的影响，在空间格局上呈现差异性，例如，城市多中心结构在缓解资源分配的同时会影响住房价格（王秀兰 等，2022）。随着生活水平的提升，居民购房选址除了考虑房屋属性，更注重周边配套公共资源是否完善，对住房条件及社区环境等与幸福感息息相关的资源格外重视（刘晔 等，2019）。城市核心区公共资源集聚所形成的区域“空间优势”，会提高区域住房吸引力（李峰清 等，2011；边艳 等，2020）。

住房价格影响因素包含三类变量，第一类是建筑特征，如住宅使用年限（Stevenson, 2004）、总建筑面积（周佳琪 等，2020）、容积率（卢新海 等，2021）、绿化率（张哲源 等，2020）和房屋朝向（唐铭杰 等，2015）等都是影响住房价格的重要指标。第二类是区位特征，即影响住房价格的核心因素（王少剑 等，2016；杨剩富 等，2016），区位特征的效用机制和作用强度与距离位置紧密相连（薛冰 等，2019），小范围内住房价格的空间差异并不明显（王洋 等，2013a）。环境类邻避设施（党艺等，2020）、绿色景观指数（Liao et al., 2022）、城市中心（秦佳睿 等，2021）、轨道交通（高峰 等，2019）、道路密度（Wang et al., 2022）、交通便利性（Luo et al., 2021）、景观环境（陈庚 等，2015）、机场设施（李伊祺 等，2021）、地铁可达性（任宏等，2019）及公交站（徐丹萌 等，2021）等区位因素均会影响住房价格。第三类是邻里特征，如商业发展环境（黄静 等，2018；Jiang et al., 2022）、医疗设施（彭保发 等，2015））、公园绿地（Trojanek et al., 2018）、社会民生（Zhan et al., 2021）、基础设施（Liu et al., 2020）、教育资源（宋正娜 等，2021）、银行（胡建飞 等，2015）和大型超市（武永祥 等，2014）等邻里范围内的公共服务因素。

研究方法上，特征价格模型（Hedonic Price Model，HPM）被广泛运用在住房价格与影响因素的关系分析上（杨剩富 等，2021；Marrouch et al.,2021），地理加权回归模型（Geographically Weighted Regression, GWR）适用于分析住房价格影响因素的空间异质性（杨俊 等，2018；Soltani et al.,2021；Hu et al., 2022）。其中，HPM 从根本上探讨的是住房价格和因素的线性回归（OLS）问题，缺乏对两者空间关系的探究，GWR 在HPM 的基础上，继承了传统回归方法的优势，进一步探究住房价格与影响因素之间的空间异质性，弥补了HPM的缺陷。GWR 使用的是唯一的带宽，意味着其对住房价格影响因素的分析，具有均质化回归特点，缺乏多尺度考量，然而，不同因素对住房价格的影响必然存在不同的尺度效应（吴超 等，2021），而多尺度地理加权回归模型（Multiscale Geographical Weighted Regression, MGWR）弥补了GWR 的缺陷，允许每个因素拥有专属带宽，以研究住房价格影响的多维空间尺度。该模型于2017年被首次提出（Fotheringham et al., 2017），2020 年后得到逐步完善和实践应用（Yu et al., 2020）。目前应用MGWR的研究较少，且主要侧重于环境污染和生态资源等方面的多尺度影响分析，极少数学者将该方法运用于住房价格影响机制探究。

鉴于此，本文尝试将MGWR 方法应用于城市住房价格实证研究中，以福州中心城区为例，采用MGWR 模型分析住房价格与影响因素的空间尺度关系，以期为中国同类城市经济可持续发展、城市规划和购房决策等提供科学依据。

1 研究区域与数据方法

1.1 研究区域

福州市（25°15′—26°39′ N、118°08′—120°31′ E）系福建省省会，山海兼备，背负山地，东临台湾海峡，是东部战区陆军机关驻地、海上丝绸之路门户及中国（福建）自由贸易试验区组成部分，具有重要的战略地位与经济贸易地位。福州市国土空间总体规划（2021—2035 年）提出“一主一副”的国土空间总体格局，“一主”即福州中心城区，“一副”即福清市区。本文将福州中心城区作为研究区域（图1），具体范围包括鼓楼区、台江区、晋安区（不含宦溪镇、寿山乡和日溪乡）、仓山区、马尾区和长乐区等城市核心区，以及闽侯县荆溪镇、上街镇等城市外围组团，总面积2 207 km2。

图1 研究区域及样本小区Fig.1 Study area and sample plots

1.2 数据来源

数据包括小区属性数据和距离数据，其中小区属性数据来源于安居客①www.anjuke.com，具体包括2021年住房平均价格、容积率、绿化率、停车位、楼龄、总户数和划片小学等信息。选择商品住宅小区作为研究对象，故别墅、自建房和商住楼不予考虑，通过筛选和剔除信息不完整的数据，最终获得3 386 个商品房住宅小区样本（见图1）。距离数据来源于百度地图②https://map.baidu.com，具体指样本小区至最近繁华中心、地铁站、公园、大学、商场、超市、医院、政府机关办事处和幼儿园等场所的距离。

1.3 研究方法

采用空间自相关分析描述研究单位之间在空间距离上的依赖程度，运用克里金插值法对住房价格进行空间平稳预测，基于多尺度地理加权回归模型（MGWR）研究住房价格影响因素的多维空间尺度。其中，以最常用的线性形式的特征价格模型为基础，住房价格为因变量，影响因素为自变量，构建MGWR模型，具体公式如下（沈体雁 等，2020）：

式中：yi代表因变量在i小区的值；bw代表模型中回归系数使用的带宽；bwj代表第j个变量回归系数使用的带宽；（ui，vi）代表样本小区的坐标；βbwj（ui，vi）代表第j个变量的回归系数，是基于局部回归得出的，且带宽具有一定的专属性，带宽即变量的作用尺度，带宽数值表示受变量影响的样本小区个数；xij代表变量j在i小区的观测值；εi为随机误差项。MGWR仍以GWR中的核函数和带宽选择为准则。本研究使用高斯核函数和AICc 准则，样本小区坐标采用WGS84坐标系（球面坐标）。

MGWR的估计与GWR使用的加权最小二乘估计明显不同，MGWR 更接近广义加性模型（王海军 等，2021），公式为：

式中：fj代表第j个变量的平滑函数，数值等于第j个变量的回归系数与观测值的乘积；xj代表变量j的数值。

广义加性模型使用后退拟合算法（Back-Fitting Algorithm）对各个平滑项进行拟合，该算法需先对所有的平滑项进行初始化设置，即先期对MGWR 中各个系数进行初步估计。初始化正常有4 种选择：①GWR估计；②半参数GWR估计；③最小二乘估计；④均设置为0。选择GWR估计为初始估计，通过计算真实值和初始化估计得到的预测值之间的差距，即初始化残差。收敛准则的判定方法有2 种——经典的残差平方和变化比例（SOCRSS）与平滑项变化比例（SOCf），由于后者收敛准则较前者更严格，更加关注变量的相对变化，故选择平滑项变化比例（SOCf）作为收敛准则，收敛阈值设定为1×10-5。

2 住房价格的空间分布特征

对福州中心城区住房价格做趋势分析可以得出（图2），住房价格在东西方向（绿色）分布相对对称且呈倒“U”型，在南北方向（蓝色）也呈倒“U”型，但差异较大，北部住宅分布比南部密集且平均住宅价格高于南部住宅。利用偏度系数、峰度系数和数据集的拟合程度对福州中心城区住房价格进行检验，经过对数变换后发现偏度系数为0.10，峰度系数为4.12，通过检验，其正态分布趋势线拟合程度高，符合正态分布，满足克里金插值的基本条件。

图2 福州市中心城区住房价格趋势分析Fig.2 Analysis of housing price trends in the central city of Fuzhou

福州中心城区住房价格空间分布呈“一主两副”的多中心模式（图3），“一主”核心区位于鼓楼区三坊七巷周围，该区域住房价格普遍高于38 000元/m2，区域内有东百中心、大洋百货等大型商业综合体，住宅围绕福州实验小学、井大小学、钱塘小学等重点学校分区划片，协和医院、福建省妇幼保健院等多所三甲医院集中在该范围内，比邻有西湖公园和左海公园。“两副”核心区分别位于晋安区泰禾广场周围和仓山区万达广场周围，晋安泰禾广场副核心区住房价格25 300元/m2，仓山万达广场副核心区住房价格29 800元/m2，2个副核心区内均有大型商业综合体、三甲医院和公园，但区域内学校为非重点学校。

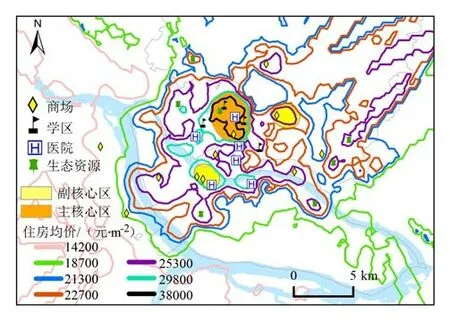
图3 福州市中心城区住房价格克里金插值结果Fig.3 Interpolation results of housing price kriging in the central city of Fuzhou

福州中心城区住房价格高的小区呈现“倾闽江、倾重点学区、倾商场、倾医院、倾城区生态资源”的空间特征（见图3）。闽江沿岸的平均住房价格比附近非沿江平均住房价格高；重点学校集中分布在鼓楼区，教育资源严重不均衡，重点学校所在片区的住房价格比非重点学校所在片区的住房价格高；大型商场周边的住房价格比远离商场的高；医院附近住房价格比远离医院高；公园附近的住房价格普遍高于远离公园的住房。

空间自相关结果显示，全局莫兰指数为0.47，Z得分31.60，P值＜0.01，通过显著性检验（即住房价格在1%显著性水平下具有正的空间相关性），住房价格在空间上相互依赖且存在集聚特征。局部空间自相关结果表明（图4），住房价格“高-高”聚类分布区域与“一主”核心区重叠，该区域拥有优越的区位和邻里特征。“低-高”聚类分布受“高-高”聚类影响，紧邻“高-高”聚类呈环状分布。“高-低”聚类零星分布在东二环以西、西三环以东和北三环以北地区，多分布在江河附近。“低-低”聚类分布在东二环东西两侧、南二环以北、南三环以北以及三环以外的郊区，交通、基础设施和教育资源等水平均较低。

图4 福州市中心城区住房价格聚类分析Fig.4 Clustering analysis of housing prices in the central city of Fuzhou

3 住房价格影响因素的多尺度空间分析

3.1 回归模型对比

剔除VIF＞5 的影响因素（繁华中心、土地等级和火车站），确保剩余影响因素之间不存在多重共线关系。对比OLS、GWR 和MGWR 回归模型（表1），MGWR模型拟合优度R2和调整后的R2均最高，AICc准则较其他2种模型明显下降，残差平方和低于另外2 个模型，可判断出3 个回归模型中，MGWR 模型拟合效果最优，稳健性最好，相较于另外2个模型，MGWR模型考虑了各影响因素的空间作用尺度，回归分析结果更可靠，故选择MGWR模型对住房价格影响因素进行空间尺度分析。

表1 OLS、GWR和MGWR模型参数描述Table 1 Description of OLS, GWR and MGWR model parameters

3.2 影响因素的多尺度空间分析

3.2.1 影响因素选择及描述 住房价格是由多方面因素综合作用形成，学者们从不同角度阐述住房价格的影响机制。例如，在国民发展水平角度上，影响因素可归为经济发展（王洋 等，2013b）、货币水平（Luciani et al., 2013）和税收政策（Du et al.,2015）三大类；在配套设施角度上，影响因素可归为社区特征、公共配套设施和交通出行三大类（徐丹萌 等，2021）；在居住条件角度上，影响因素可归为建筑特征（王洋 等，2014）、邻里特征（薛冰等，2019）和区位特征（孙倩 等，2015）三大类。本文结合以上学者研究，试图从配套设施和居住条件角度出发，从建筑特征、邻里特征、区位特征、公共配套设施、交通出行等类别中选取适合的影响因素进行分析，具体如表2所示。

表2 福州市中心城区住房价格影响因素描述Table 2 Description of factors influencing housing prices in the central city of Fuzhou

3.2.2 带宽及空间异质性分析 OLS、GWR 和MGWR 模型的带宽数值及检验P值如表3 所示。OLS 是在全局范围内的拟合，不能体现空间差异，即影响因素均为全局尺度，共用1个带宽，带宽数值为总样本量3 386。GWR回归结果可以体现影响因素的空间差异，但不能体现其空间差异程度，即影响因素的作用位置虽不同，但在GWR 表达下尺度范围均一致，该尺度范围以最优带宽332 表示。OLA 和GWR 都只有1 个带宽，忽略了影响因素的空间异质性程度，对住房价格影响因素的空间解释精准度不足（吴超 等，2021）。相比之下，MGWR模型中各影响因素均有专属带宽，带宽取值范围为[46, 3 386]，表明MGWR不仅强调影响因素的空间异质性，而且能更加精准地解释影响因素的空间作用尺度。影响因素的带宽越大，表明该因素在大尺度范围甚至全局尺度范围内影响住房价格；带宽越小，表明该因素在局部尺度范围内影响住房价格（沈体雁 等，2020）。

表3 OLS、GWR和MGWR模型带宽比较Table 3 Comparison of bandwidth of OLS, GWR and MGWR model

由表3 可知，绿化率、停车位、总户数等9 个影响因素检验P值不显著，表明上述影响因素在MGWR 模型中没有显著作用，故不多作解释。容积率、楼龄、地铁站、长途汽车站、大学、商场、医院和小学等级检验P值显著，表明MGWR 模型中，上述影响因素对住房价格具有显著作用，故而对具有显著影响力的因素详细解释与分析。容积率、楼龄、商场、医院和小学等级带宽分别为1 217、46、68、239、46，上述因素作用尺度均属于局部尺度，即只在局部范围内对住房价格产生显著影响。其中，楼龄、商场和小学等级的带宽分别占整体样本的1.36%、2.01%和1.36%，故这些因素的作用尺度接近街道尺度，远小于其他影响因素，空间异质性大，对住房价格的空间影响尺度小；容积率和医院的带宽分别占整体样本的35.96%和7.06%，接近区级行政尺度，空间异质性中等，对住房价格的空间影响处于中级尺度。地铁站、长途汽车站和大学带宽分别为3 386、3 308、3 315，几乎接近整体样本总数，空间异质性小，对住房价格的空间影响尺度大，属于全局尺度。

3.2.3 回归系数结果 表4显示，显著影响因素对住房价格的作用强度平均值绝对值由大到小依次为小学等级（0.237）、楼龄（0.189）、长途汽车站（0.110）、商场（0.089）、容积率（0.088）、大学（0.069）、医院（0.052）和地铁站（0.029）。其中，小学等级、长途汽车站、容积率、医院与住房价格呈正相关，楼龄、商场、大学和地铁站与住房价格呈负相关。即，区域内住房价格随容积率的增加、小学等级的提升、距附近汽车站距离的增加、距邻近医院距离的增加而上升；住房价格随小区楼龄的增加、距最近商场距离的增加、距邻近大学距离的增加、距附近地铁站距离的增加而下降。

表4 MGWR模型回归系数结果Table 4 MGWR model regression coefficient results

从局部显著因素的MGWR 回归系数及空间分布看，容积率、楼龄、商场、医院以及小学等级的显著样本占总样本分别为90.7%、39.9%、23.8%、30.5%以及49.0%。其中，容积率带宽数值为1 217，空间异质性中等，回归系数的空间分布（图5-a）取值区间为 [0.041, 0.166]，空间分布上从鼓楼区向四周呈环状递减，衰减速度先快后慢，各方向的衰减趋势相似。理论上，容积率代表居住密度，密度越大居住舒适度越低，在不考虑其他因素的情况下，住房价格应随着容积率的增加而降低，但鼓楼区公共资源集中，“空间优势”显著，居民为了享受便利的公共教育等资源，愿意接受高密度的居住环境，并且离市中心距离越近，购买意愿越强烈。楼龄带宽数值为46，空间异质性大，回归系数的空间分布（图5-b）取值区间为 [-1.391, 1.000]，楼龄对住房价格的影响在大部分区域为负，即住房价格随楼龄的增加而降低，因为房屋折旧会造成住房部分功能的损失，然而，楼龄又对小部分住宅小区影响为正，原因在于重点小学辐射范围内的片区，属于传统意义上的“老破小”学区房，即便楼龄增加，住房价格不降反增。商场带宽数值为68，空间异质性大，回归系数的空间分布（图5-c）取值区间为 [-1.690, 0.645]，商场对绝大部分的住房价格影响为负，即大部分紧邻商场的小区住房价格比商场外围的小区价格更低，原因在于商场噪声污染大、交通拥挤并且人流量密集，会造成紧邻商场的小区居住品质下降，紧邻商场的住房对居民的吸引力降低，相比之下，商场外围小区在享受便利的购物条件的同时，拥有更安静舒适的居住环境，居民对商场外围小区的购买需求更强。医院带宽数值为239，空间异质性中等，回归系数的空间分布（图5-d）取值区间为[-0.344, 0.434]，医院对绝大部分小区的住房价格起正向影响，对小部分小区的住房价格起负向影响，说明大部分小区距离医院越近，住房价格越高，而存在小部分小区可能主要受到其他因素影响，故而医院对小部分小区住房价格影响不大或为负影响。小学等级带宽数值46，空间异质性大，回归系数的空间分布（图5-e）取值区间为 [-0.985, 1.294]，小学等级对主城区的住房价格影响为正，对郊区小区的住房价格影响为负，表明主城区教育资源优质且集中，周围小区住房价格受“教育红利”的影响呈高水平，而郊区优质教育资源稀缺，住房价格受小学等级影响不大，主要受其他因素的影响，故而，郊区小学等级对住房价格影响不大或为负影响。

图5 福州市中心城区MGWR模型回归系数的空间分布Fig.5 Spatial distribution of regression coefficients of the MGWR model in the central city of Fuzhou

从全局显著因素的多尺度地理加权回归系数结果及空间分布看，地铁站、长途汽车站、大学的显著样本占总样本的100%，3 个因素的带宽趋近样本总数，对研究范围内所有研究小区均起显著影响。其中，地铁站带宽数值为3 386，空间异质性小，回归系数的空间分布（图5-f）取值区间为[-0.033,-0.013]，小区离最近地铁站的距离增加导致住房价格下降，说明居民对离地铁站近的住房有更强的购买意愿，从回归系数空间分布看，地铁1号线对住房价格的影响要高于地铁2号线，原因可能是地铁1号线运行时间较长且贯穿福州中心城区繁荣地带。长途汽车站带宽数值为3 308，空间异质性小，回归系数的空间分布（图5-g）取值区间为 [0.084, 0.113]，小区离最近长途汽车站的距离增加导致住房价格增加，不考虑其他因素的影响，理论上距离增加会造成交通不便，从而导致住房价格的下降，但实际上长途汽车站对住房价格反而起抑制作用，参考福州市自然资源和规划局（2022）公示的《福州城市综合交通规划（2020—2035 年）》可知，长途汽车站多分布在远离人群的郊区，因为车站附近，人口流动性强、噪声嘈杂、犯罪率较高及居住舒适度低等问题会对附近居民造成负面影响，即便汽车站交通便利，其住房吸引力也会有所减弱。大学带宽数值为3 315，空间异质性小，回归系数的空间分布（图5-h）取值区间为 [-0.075,-0.038]，小区住房价格随其离最近大学的距离增加而下降，大学周边不仅拥有完善的公共服务设施，而且具有优质的人文环境，所以其周边住房对居民吸引力强。

4 结论与讨论

4.1 结论

本文以福州中心城区为研究区域，运用空间统计方法和多尺度地理加权回归模型等方法，分析了福州中心城区住房价格的空间分布特征及其价格影响因素，并得到以下主要结论：

1）从东西方向和南北方向上看，福州中心城区住房价格均呈倒“U”型，且东西方向对称，南北方向上北部住房较密集且价格高于南部；住房价格呈现“一主两副”的多中心分布模式，“一主”核心区位于鼓楼区三坊七巷周围，“两副”核心区分别为晋安区泰禾广场和仓山区万达广场。住房价格高的小区呈现“倾闽江、倾重点学区、倾商场、倾医院、倾生态资源”的空间特征。

2）对于本研究MGWR 模型较OLS 模型和GWR 模型拥有更好的拟合效果和稳健性，回归分析结果更加可靠。根据带宽大小将各显著影响因素划分为作用尺度接近街道、作用尺度接近区级行政区、作用尺度为福州中心城区全局3种类型，楼龄、商场和小学等级等作用尺度接近街道，该类因素带宽小，空间异质性大，只影响街道范围内小区的住房价格；容积率和医院等作用尺度接近区级行政区，该类因素带宽中等，空间异质性中等；地铁站、长途汽车站和大学等作用尺度为福州中心城区全局，该类因素带宽趋近样本总数，空间异质性小，对全局范围内的小区住房价格均有影响。

3）从MGWR模型回归结果的平均值的绝对值看，对住房价格的作用强度由大到小依次为小学等级（0.237）、楼龄（0.189）、长途汽车站（0.110）、商场（0.089）、容积率（0.088）、大学（0.069）、医院（0.052）、地铁站（0.029）。住房价格随容积率增加、小学等级提升、距附近汽车站距离增加、距邻近医院距离增加而上升，随小区楼龄增加、距最近商场距离增加、距邻近大学距离增加、距附近地铁站距离增加而下降。

4.2 讨论

住房价格受到各种类型因素的影响，各要素的影响范围尺度不尽相同，尺度作为地理学研究的基本范畴，是现象阐述的重要参考视角，细分不同类型影响因素的作用强度及空间尺度对城市规划具有重要意义。福州市作为东部沿海二线城市，住房价格空间分布具有地域特色，呈现多中心模式，本研究对拥有独特地域特色的多核心城市具有针对性借鉴意义。首先，城市规划需秉持因地制宜原则，针对城市住房价格空间格局和分布规律进行恰当地规划布局，减缓住房价格空间分布差异带来的困境，促进经济可持续发展。其次，带宽数值较小代表其空间异质性较大，该类因素作用范围为局部尺度，例如商场、小学等级和医院，即在小范围内对小区住房价格产生影响，在规划布局时应着重考虑具体影响因素的空间作用效果，合理分配基础设施服务和教育资源等公共资源。带宽数值较大的影响因素在全局尺度上对住房价格产生影响，例如地铁站、长途汽车站和大学，对该类公共基础设施进行空间规划时需从大尺度空间范围进行评估和考量。此外，影响因素的作用强度是城市规划需考虑的重要因素之一，针对拉动力强的影响因素，如小学等级、楼龄与商场，需合理规划资源分配的数量以及空间位置布局，提出适宜的规划方案，最终达到拉动经济稳步增长和满足居民购买意愿的目的。

本文在空间视角上对住房价格分布特征及其影响因素的作用尺度进行阐述，对城市规划和居民购房具有一定的指导意义。但受限于数据获取和分析的时限性，在时间尺度分析及住房单元属性特征等方面仍有所欠缺。具体而言，本文仅选取2021年的数据，缺乏住房价格长期空间分布特征及影响因素的时间变化趋势的分析；研究对象为小区，忽略了住房单元面积、朝向等属性特征。未来将继续深化研究，以期在时空视角、小区和单元层面获得更加完善的研究结论。