黄河流域制造业集聚对城市绿色经济效率的影响

孟望生，郑延钦，张扬

（1.甘肃政法大学a.商学院；b.经济学院，兰州 730070；2.陕西师范大学国际商学院，西安 710119）

0 引言

黄河流域是我国北方重要的生态安全屏障和经济发展区域。然而长期以来的粗放型经济增长方式使得黄河流域暴露出生态环境脆弱、资源浪费严重、经济结构转换动能不足等一系列问题，这些问题阻碍了黄河流域经济高质量发展。党的十八大以来，习近平总书记高度重视黄河流域生态文明建设，并于2019年9月明确提出“黄河流域生态保护和高质量发展是重大国家战略”，这一战略的提出为黄河流域探索以经济绿色发展为导向的高质量发展路径提供了基本遵循。改革开放40多年来，黄河流域内出现了明显的制造业及其关联产业向区域中心城市集中的现象，即制造业集聚现象。制造业集聚过程往往与人口流动、资本循环、技术创新等经济活动相互关联，势必会对城市绿色经济效率产生影响。那么，黄河流域制造业集聚将如何影响城市绿色经济效率？又会对城市间绿色经济效率差距产生哪些影响？回答上述问题，对于推动黄河流域生态保护和高质量发展国家战略的顺利实施具有重要意义。

现有关于制造业集聚影响城市绿色经济效率的研究可归纳为三类：一是制造业集聚对城市绿色经济效率的影响特征，主要包括线性变化特征[1]和非线性变化特征[2]。二是制造业集聚对城市间绿色经济效率差距的影响特征，雷鹏（2011）[3]以制造业集聚与工业总产值的关系为视角，研究发现制造业集聚会拉大区域经济发展差距。三是外部因素对制造业集聚影响城市绿色经济效率的调节作用，主要聚焦产业结构变迁[4]等中间环节因素和环境规制[5]等制度配套因素。综上所述，现有研究大多集中在全国范围内的城市或行业层面，而针对黄河流域这一重点区域的研究相对匮乏，同时，现有研究对制造业集聚引致的城市间绿色经济效率差距的关注甚少，对影响城市绿色经济效率的重要因素如绿色技术创新和外商投资的关注不够。基于此，本文以黄河流域城市数据为样本，考察制造业集聚对城市绿色经济效率、城市间绿色经济效率差距的影响，同时检验绿色技术创新和外商投资对流域内制造业集聚影响城市绿色经济效率的调节作用，为黄河流域经济绿色发展水平的提升提供参考。

1 理论分析与研究假设

1.1 制造业集聚对城市绿色经济效率的影响

制造业集聚会通过马歇尔外部性、雅各布斯外部性与波特外部性促进城市绿色经济效率的提升。马歇尔外部性强调，制造业集聚能够加强企业间的技术交流，既有助于形成并共享大规模劳动力市场，又能够促进集聚地企业和劳动力进一步推进专业化分工，降低制造业企业及其关联性企业的生产成本，从而改善绿色经济效率。雅各布斯外部性强调，制造业集聚能够推动集聚地不同产业融合发展，多样化的产业体系能够形成协同效应、创新效应、知识和技术溢出效应，从而有益于绿色经济效率的改善。波特外部性强调，制造业集聚引起的竞争效应能够激发集聚地企业增加科研投入，推动企业自发进行技术改造与绿色转型，从而有利于绿色经济效率的改善。与此同时，制造业集聚还会通过拥挤效应、污染天堂效应与资源诅咒效应抑制城市绿色经济效率的提升[6]。据此，本文提出：

假设1：黄河流域制造业集聚对城市绿色经济效率的影响存在不确定性，需要通过实证研究加以确定。

1.2 制造业集聚对城市间绿色经济效率差距的影响

制造业集聚会通过“虹吸效应”扩大城市间绿色经济效率差距。黄河流域内不同城市间在人口数量、资源禀赋、科技实力等方面均存在较大差异，制造业作为人口、资源和科技密集型产业，通常会向这些方面发展基础较好的中心城市集聚，这一集聚过程会使中心城市形成比周边中小城市更加完备的产业体系。一方面，完备的产业体系会产生规模效应，来提高中心城市制造业企业的经济效益，另一方面，还会产生知识和技术溢出效应与创新效应，来提高中心城市制造业企业的生产效率，进而实现绿色经济效率的提升。集聚中心城市绿色经济效率的提升会进一步增强其吸引力，即对周边中小城市产生“虹吸效应”[7]，从而进一步扩大集聚中心城市与周边中小城市绿色经济效率的差距。此外，制造业集聚还会通过“马太效应”扩大城市间绿色经济效率差距。据此，本文提出：

假设2：黄河流域制造业集聚会扩大城市间绿色经济效率差距。

1.3 绿色技术创新、外商投资水平对制造业集聚影响城市绿色经济效率的调节作用

绿色技术创新会对制造业集聚影响城市绿色经济效率起调节作用。绿色技术创新作为创新的关键构成部分，为制造业集聚发挥规模效应、创新效应、协同效应提供了科技支撑。当流域内绿色技术创新水平较低时，其表现出的技术创新滞后、生产效率低下会制约制造业集聚规模效应的发挥，进而抑制绿色经济效率的改善。当流域内绿色技术创新水平提高到一定程度时，整体的生产技术与工艺得以改进，污染物和废弃物处理技术达到绿色低碳生产的标准，对人才、技术、资金的吸引力不断增强，此时制造业集聚产生的创新效应、协同效应有益于绿色经济效率的改善；当流域内绿色技术创新水平进一步提高引发制造业过度集聚时，城市资源供给不足带来的拥挤效应会加剧企业间的竞争，降低资源配置效率，削弱制造业集聚对绿色经济效率的正向影响。据此，本文提出：

假设3：黄河流域制造业集聚对城市绿色经济效率的影响存在基于绿色技术创新水平的门槛效应。

外商投资也会对制造业集聚影响城市绿色经济效率起调节作用。外资引进初期，由于流域内外资引进愿望迫切、环保意识低、环境规章制度不完善，加之流域内自然资源丰富，因此很容易产生外商投资的“污染避难所”效应，即外商会偏向于投资资源相关类的污染型企业，此时制造业集聚会加剧地区环境污染，从而抑制绿色经济效率的改善。随着外商投资水平提高到一定程度后，流域内环保意识增强、环境规制趋于完善，此时，一方面，外商会跨区域甚至跨国调配要素和技术以提升其在流域内投资企业的绿色生产效率，另一方面，制造业企业间的“学习效应”会推动流域内所有制造业企业进行技术升级和绿色转型，并且外商投资企业带来的竞争效应能够提高制造业企业的准入门槛，进一步优化资源配置，发挥制造业集聚带来的资源配置效应，最终实现对绿色经济效率的改善。据此，本文提出：

假设4：黄河流域制造业集聚对城市绿色经济效率的影响存在基于外商投资水平的门槛效应。

2 研究设计

2.1 模型构建

为考察黄河流域制造业集聚对城市绿色经济效率的影响是否存在非线性变化特征，同时考虑到城市绿色经济效率的变化可能是一个具有路径依赖的动态过程，本文构建如下动态面板模型：

其中，Geei,t为绿色经济效率，Geei,t-1为绿色经济效率的一阶滞后项，Aggi,t为制造业集聚水平，Xi,t为控制变量集，i为城市，t为年份，α0、α1、α2、α3、α4为待估参数，μi和νt分别为城市固定效应和时间固定效应，εi,t为随机扰动项。

为检验黄河流域制造业集聚对城市间绿色经济效率差距的影响，构建如下模型：

其中，Gee_gapi,t为城市间绿色经济效率差距，Gee_gapi,t-1为城市间绿色经济效率差距的一阶滞后项。

为探究不同发展条件下，黄河流域制造业集聚对城市绿色经济效率的影响是否会发生变化，借鉴Hansen（1999）[8]的门槛回归法构建面板门槛模型。构建单一门槛效应模型如下：

构建双重门槛效应模型如下：

其中，qi,t为门槛变量，包括绿色技术创新水平（Gna）与外商投资水平（Fdi）；θ1、θ2为对应门槛值；I(·)为示性函数。

2.2 变量选取

（1）被解释变量：绿色经济效率（Gee）和城市间绿色经济效率差距（Gee_gap）。混合距离EBM模型能够较好地处理径向与非径向同时存在的投入产出关系，因此，本文采用基于EBM方向性距离函数的Malmquist-Luenberger（ML）指数对绿色经济效率进行测度，具体公式如下：

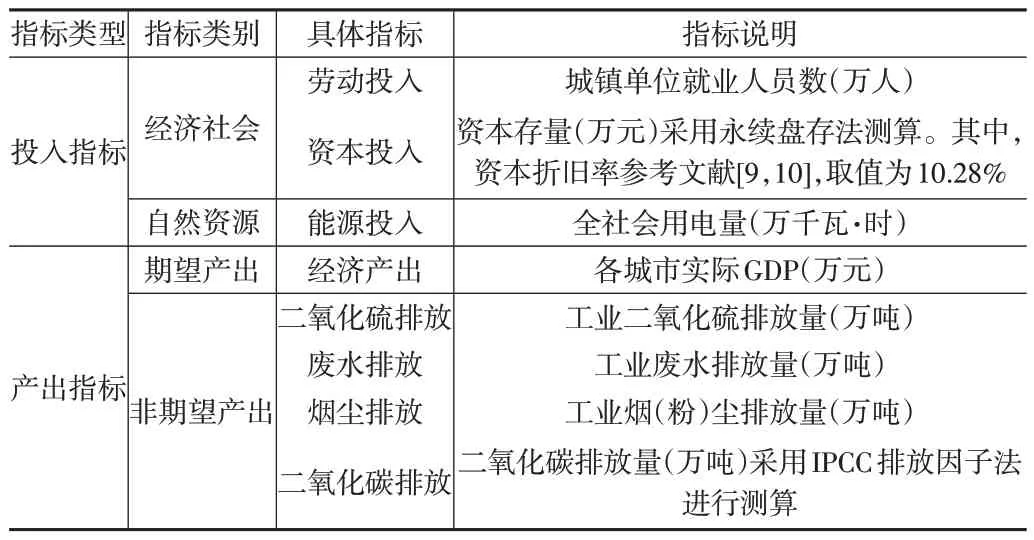
表1 绿色经济效率的投入产出指标

对于城市间绿色经济效率差距（Gee_gap），参考卞元超等（2018）[11]的做法，采用各年度绿色经济效率的离差来衡量，具体计算公式为各年度绿色经济效率离差=指定年度某城市绿色经济效率测度值-该年度流域内所有城市绿色经济效率均值。为保证结果分析的一致性，对离差值取绝对值。

（2）核心解释变量：制造业集聚水平（Agg）。现有研究普遍采用行业集中度（CRn指数）、赫芬达尔-赫希曼指数（HHI）、区位熵（E指数）与Ellision-Glaeser集聚指数（EG指数）来测算并衡量制造业集聚水平。其中，CRn指数在行业空间集聚水平的刻画上有所欠缺；HHI与EG指数需要将数据精确到企业层面，数据获取的难度较大；相较而言，区位熵能够缩小区域规模间的差异，客观展现制造业集聚的专业化程度。因此，采用区位熵来衡量制造业集聚水平，借鉴张平淡和屠西伟（2021）[4]的研究，计算公式如下：

其中，i为城市，t为年份，Zi,t为城市i第t年制造业就业人数，ΣiZi,t为第t年制造业总就业人数，ΣsZi,t为城市i第t年所有产业总就业人数，ΣiΣsZi,t为第t年所有产业总就业人数。

（3）门槛变量：绿色技术创新水平（Gna）和外商投资水平（Fdi）。对于绿色技术创新水平（Gna），采用绿色专利申请量来衡量，以绿色发明专利申请量与绿色实用新型专利申请量的总和来表示。外商投资水平（Fdi），采用实际利用外商投资额占GDP的比重来衡量，其中实际利用外商投资额按照历年人民币平均汇率进行折算。

（4）控制变量。参考已有研究，选择以下控制变量：（1）人力资本水平（Hc），采用普通高等学校在校师生人数占城市总人口的比重来衡量。（2）产业结构（Is），采用第三产业产值与第二产业产值的比值来衡量。（3）经济发展水平（Pgdp），采用人均GDP来衡量。（4）政府干预（Gov），采用政府财政支出占GDP的比重来衡量。（5）环境规制（Er），借鉴任晓松等（2020）[12]的研究，采用熵值法计算出的环境规制综合指数的倒数来衡量。（6）科技投入（Tec），采用财政经费中科技支出占GDP的比重来衡量。

2.3 数据来源

考虑到黄河仅流经了四川西北部的小部分区域，因此未将四川纳入研究样本。另外，由于行政区划调整和数据可得性问题，本文最终采用2006—2020年黄河流域8个省份（剔除四川）的40个城市作为研究样本。数据主要来源于历年《中国城市统计年鉴》《中国能源统计年鉴》《中国环境统计年鉴》《中国工业经济统计年鉴》以及各省份统计年鉴、Wind数据库、EPS全球统计数据库以及中经网统计数据库。个别缺失数据采用插值法补齐，涉及价格的指标均以2006年为基期进行相应价格指数折算。各变量的描述性统计见表2。

表2 变量的描述性统计

3 实证结果分析

3.1 基准回归结果分析

本文采用两步系统GMM方法对模型进行基准回归，回归结果如下页表3所示。从检验结果来看，AR（1）的P值小于0.1，AR（2）的P值大于0.1，说明差分后的扰动项只存在一阶序列相关，不存在二阶序列相关；Sargan检验的P值大于0.1，说明选择的工具变量满足有效性要求。

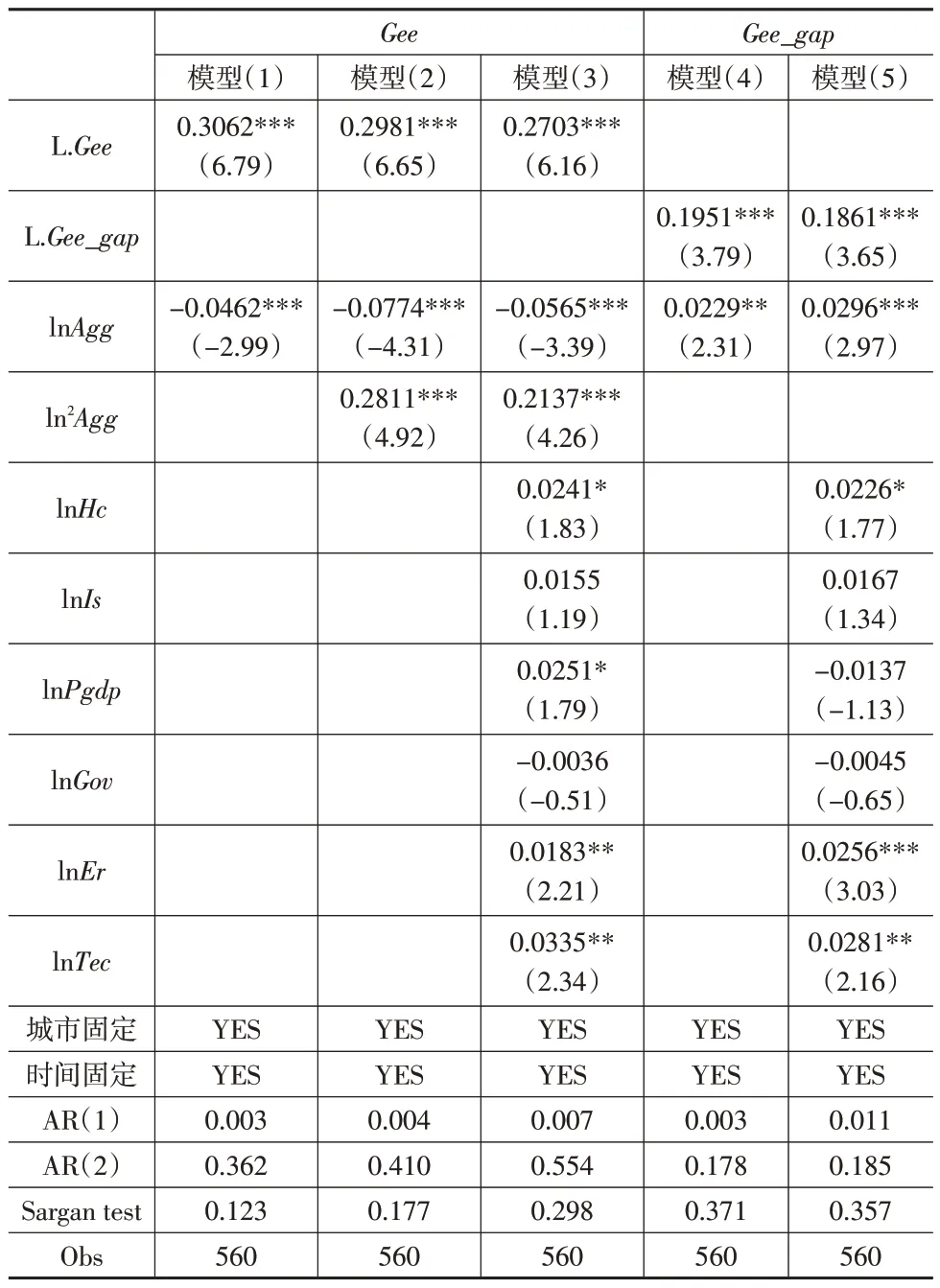
表3 基准回归结果

模型（2）和模型（3）的结果均显示，制造业集聚一次项的估计系数显著为负，二次项的估计系数显著为正，说明黄河流域制造业集聚对城市绿色经济效率的影响呈现“U”型变化特征，由此假设1得以确定。究其原因，当流域内制造业集聚水平较低时，环境规制不健全和有利于资源开发政策等的“筛选”功能会使更多高污染、低效率的制造业企业汇聚，此时集聚会阻碍绿色经济效率的改善。随着集聚水平不断提升，一方面资源配置得到优化，另一方面环境规制和有利于制造业企业的制度逐步完善倒逼企业加大环保投入、降低污染排放，最终实现对绿色经济效率的改善。由模型（3）计算可知，“U”型曲线的拐点值位于lnAgg为0.132处，流域内大部分城市的制造业集聚水平小于这一数值，说明大部分城市的制造业集聚水平尚处于抑制绿色经济效率提升的阶段。控制变量中，人力资本水平、经济发展水平、环境规制与科技投入的估计系数均显著为正，说明这些因素均有利于绿色经济效率的改善；产业结构的估计系数不显著，这可能与黄河流域第二、三产业比重不协调有关；政府干预的估计系数为负但不显著，说明地方政府可能存在忽视环境治理等问题。

模型（4）报告了黄河流域制造业集聚对城市间绿色经济效率差距的影响，模型（5）是在模型（4）的基础上进一步纳入控制变量后的回归结果。结果显示，制造业集聚的估计系数显著为正，这说明黄河流域制造业集聚会扩大城市间绿色经济效率差距，这也进一步验证了假设2。控制变量中，人力资本水平、环境规制与科技投入的估计系数均显著为正；产业结构的估计系数为正、经济发展水平与政府干预的估计系数为负，但均不显著。这说明当前人力资本水平提升、环境规制强度加强和科技投入增加均会拉大流域内城市间绿色经济效率差距；以第三产业产值与第二产业产值的比值为衡量指标的产业结构变迁会扩大流域内城市间绿色经济效率差距，流域内整体经济发展水平提升和以财政支付为主要手段的政府干预加强有助于缩小城市间绿色经济效率差距，但效果均不明显。

模型（1）至模型（3）的结果显示，以城市绿色经济效率为被解释变量，解释变量中城市绿色经济效率的一阶滞后项均显著为正；模型（4）至模型（5）的结果显示，以城市间绿色经济效率差距为被解释变量，解释变量中城市间绿色经济效率差距的一阶滞后项均显著为正。这说明流域内上一年度的城市绿色经济效率能够对当年的城市绿色经济效率产生助推作用，即城市绿色经济效率存在路径依赖；同样地，流域内城市间绿色经济效率差距也存在路径依赖，即如果不进行干预，城市间绿色经济效率差距就具有不断扩大的发展趋势。

3.2 异质性分析

考虑到黄河流域各地区经济发展水平、制造业集聚水平均存在较大差异，总体样本的估计结果可能会忽略地区异质性。为考察不同地理区位下制造业集聚对城市绿色经济效率、城市间绿色经济效率差距的影响情况及其差异性，本文将研究样本分为上、中、下游地区分别进行估计，结果见表4。

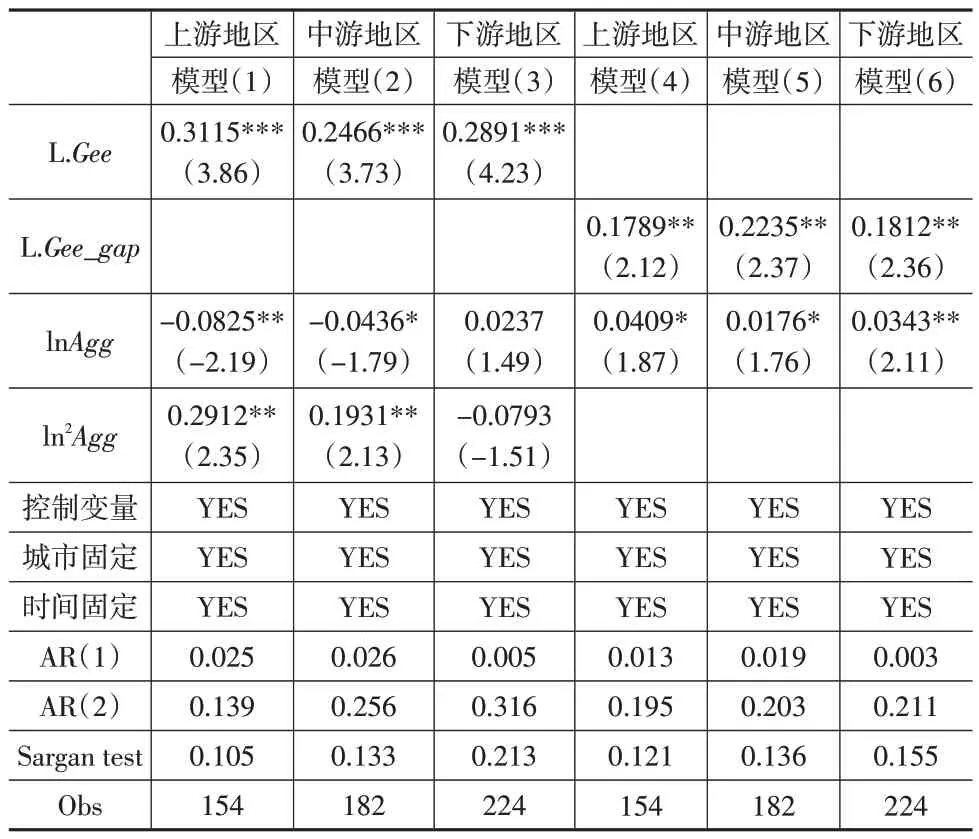
表4 异质性回归结果

模型（1）至模型（3）的结果显示，流域内上、中游地区制造业集聚一次项的估计系数显著为负，二次项的估计系数显著为正，与全流域的估计结果一致；下游地区制造业集聚一次项、二次项的估计系数均不显著，仅加入制造业集聚的一次项时（限于篇幅，结果未在文中呈现），下游地区制造业集聚的估计系数显著为正。这说明在上、中游地区，制造业集聚对城市绿色经济效率的影响呈现先抑制后促进的“U”型变化特征；在下游地区，制造业集聚对城市绿色经济效率的影响仅呈现促进作用。模型（4）至模型（6）的结果显示，流域内三大地区制造业集聚的估计系数均显著为正，且上游地区制造业集聚的估计系数最大，下游次之，中游最小。这说明流域内三大地区制造业集聚均会扩大城市间绿色经济效率差距，且这种扩大效应呈现上、下、中游地区依次递减的趋势，也进一步说明当前上游地区由制造业集聚引致的城市间经济绿色发展不平衡问题最为突出。

3.3 内生性分析

考虑到变量之间可能存在反向因果关系而产生内生性问题，本文采用两阶段最小二乘法（2SLS）来解决这一问题。模型中涉及制造业集聚的一次项和二次项两个内生变量，因此需构造两个工具变量。本文从地理因素和历史因素出发，借鉴李治国等（2022）[13]的做法，以城市地形起伏度与年份虚拟变量的交互项作为第一个工具变量；同时，借鉴章元和刘修岩（2008）[14]的思路，以1933年城市是否通铁路与上一年固定资产投资的交互项作为第二个工具变量。从表5中第二阶段的估计结果可知，黄河流域制造业集聚对城市绿色经济效率的影响仍呈现“U”型变化特征。同样地，黄河流域制造业集聚对城市间绿色经济效率差距具有显著正向影响，与前文估计结果基本一致。

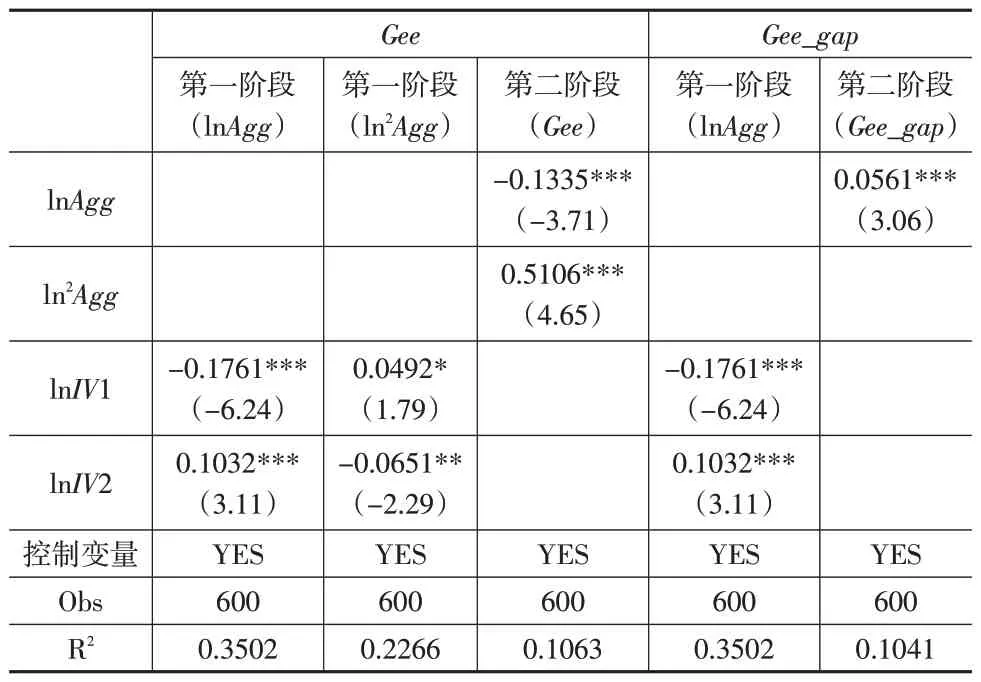
表5 2SLS估计结果

3.4 稳健性检验

（1）剔除资源禀赋较高城市。考虑到资源禀赋较高城市的产业政策及发展规划与其他城市可能存在较大差异，采用“采矿业就业人数与城镇就业人数之比”来刻画地区资源禀赋水平，并将流域内资源禀赋水平前十名的城市进行剔除后再进行回归。（2）替换核心解释变量。采用EG指数对黄河流域制造业集聚水平进行二次测算，将测算结果作为核心解释变量的又一衡量指标对模型进行重新估计。（3）剔除中心城市。由于黄河流域中心城市可能在政策扶持力度上与其他城市存在较大差异，为排除这种差异可能引起的估计结果偏误，借鉴师博（2020）[15]对黄河流域中心城市的界定，将黄河流域中心城市剔除后再回归。由估计结果可知，制造业集聚一次项、二次项的估计系数符号均与基准回归结果保持一致，说明前文结论是稳健的。

3.5 门槛效应检验

3.5.1 门槛效应估计结果

在进行面板门槛模型回归分析之前，要先进行门槛效应检验。本文采用Bootstrap自抽样法重复抽样500次，估算出F统计量和P值。门槛效应检验结果见表6，能够发现绿色技术创新水平存在双重门槛，外商投资水平存在单一门槛。

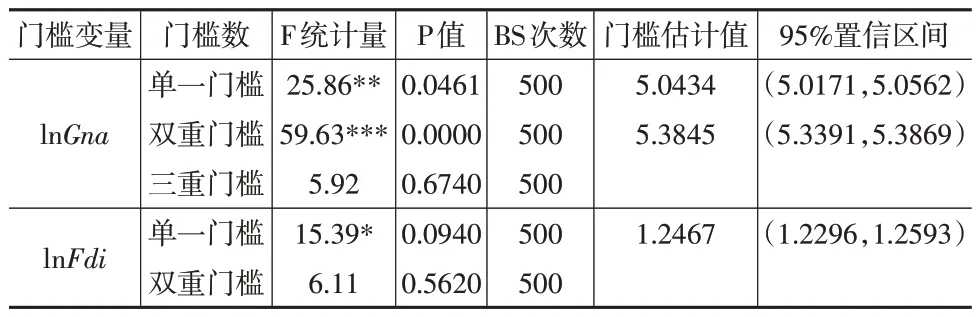
表6 门槛效应估计结果

3.5.2 门槛回归结果

表7报告了分别以绿色技术创新水平与外商投资水平作为门槛变量的门槛模型回归结果。模型（1）的估计结果显示，当lnGna低于第一个门槛估计值5.0434时，制造业集聚的回归系数为-0.0593且在10%的水平上显著，当lnGna介于两个门槛估计值之间时，制造业集聚的估计系数为0.1566且在1%的水平上显著，当lnGna高于第二个门槛估计值5.3845时，制造业集聚的影响系数为0.0373且在5%的水平上显著。这说明当绿色技术创新水平较低时，制造业集聚不利于绿色经济效率的改善；当绿色技术创新水平跨过一定的门槛值后，制造业集聚能够显著促进绿色经济效率的改善；当绿色技术创新水平跨过更高的门槛值后，制造业集聚对绿色经济效率的助推作用减弱，由此假设3得证。

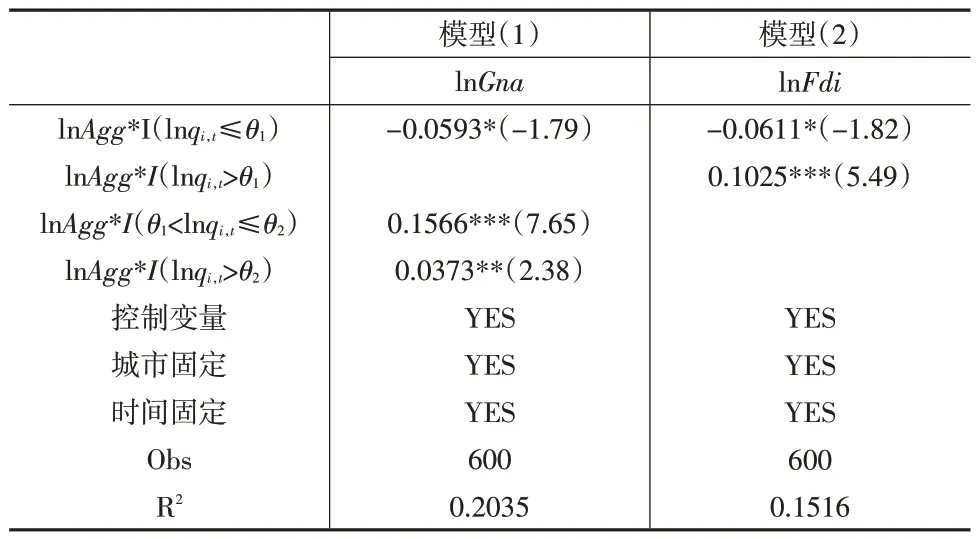
表7 门槛回归结果

模型（2）的估计结果显示，当lnFdi低于门槛估计值1.2467时，制造业集聚的回归系数为-0.0611且在10%的水平上显著；当lnFdi跨过门槛估计值后，制造业集聚的估计系数为0.1025且在1%的水平上显著。这说明当外商投资水平较低时，制造业集聚会抑制绿色经济效率的改善；当外商投资水平跨过一定的门槛值后，制造业集聚会促进绿色经济效率的改善，由此假设4得证。

4 结论

本文基于2006—2020年黄河流域城市面板数据，运用两步系统GMM实证检验了黄河流域制造业集聚对城市绿色经济效率、城市间绿色经济效率差距的影响，并基于面板门槛模型考察了制造业集聚对城市绿色经济效率的非线性影响，得出如下结论：（1）黄河流域制造业集聚对城市绿色经济效率的影响呈现“U”型变化特征，同时制造业集聚还会扩大城市间绿色经济效率差距，导致流域内经济绿色发展不平衡进一步加剧；此外，无论是城市绿色经济效率还是城市间绿色经济效率差距均存在路径依赖。（2）黄河流域制造业集聚无论是对城市绿色经济效率还是对城市间绿色经济效率差距的影响，都存在区域异质性。（3）黄河流域制造业集聚对城市绿色经济效率的影响存在基于绿色技术创新水平和外商投资水平的门槛效应。