金银花静电除杂装置设计与试验

王凤花 林玉红 赖庆辉 王永杰 田保宁 苏 微

(1.昆明理工大学现代农业工程学院, 昆明 650500; 2.云南师范大学能源与环境科学学院, 昆明 650500)

0 引言

近几年金银花的种植面积和产量接连增长。但在金银花的采摘、运输过程中,容易混入梗、叶和编织袋丝等杂质[1-3],影响产品的质量和价格。因此,在金银花的初加工过程中,除杂处理是最为关键的环节之一。然而,当前金银花的除杂方式仍以人工为主,存在效率低和成本高的问题,严重制约了金银花产业的发展。解决金银花除杂效率低的问题对于提高金银花市场价值尤为重要。

风选技术、光电技术、振筛技术以及静电分离技术是农产品加工过程中常用的除杂技术[4-8]。其中风选技术基于农产品与杂质的悬浮速度不同,一般用于清除较轻的杂质[9]。而利用光电技术研制的色选机通常适用于大小相近、颜色差异大的农产品,如枸杞、大米和花椒等[10-12]。振筛技术根据农产品与杂质外形尺寸的差异,通过更换不同间隙的筛网进行除杂分级[13]。以上技术对于金银花中梗、叶的除杂具有一定分离效果,但对于编织袋丝这类形状细长、与金银花质量差异不明显的杂质,除杂效果不明显。

静电分离技术是利用静电吸附原理进行混合物分离的一类技术[14],能将介电性能不同的混合物分离,不受形状、颜色等物料特性干扰。静电分离技术早期多用于分离工业领域中金属与非金属材料[15],目前静电分离技术也逐步进入农业领域[16]。郭淑霞等[17]研制了高压静电籽棉残膜分离装置,实现了残膜与籽棉的分离。JAFARI等[18]将静电分离技术应用于分离麦粒和秸秆,通过仿真预测了麦粒与秸秆的分离轨迹,仿真结果与样机试验结果吻合较好。杨永发等[19]在制茶过程中,通过控制茶叶与茶梗的含水量实现静电分离。综上所述,静电分离技术在解决质量相近、形状相似的物质难以分离的问题上相比于其他除杂技术更具优势。静电分离技术为金银花除杂问题提供了一种解决思路。

为解决当前金银花中的编织袋丝去除效果不佳的难题,本文依据静电分离技术,设计一种金银花静电除杂装置并进行除杂试验。对金银花和编织袋丝的分离过程进行理论分析,基于COMSOL仿真和单因素试验确定除杂装置主要结构参数。对影响除杂性能的3个关键因素开展Box-Behnken试验,进行参数优化,确定最优工作参数。

1 除杂装置工作原理与设计

1.1 除杂机理理论分析

为验证静电分离技术对金银花除杂的可行性,以常见的辊式静电分离结构为例,对金银花和编织袋丝进行受力分析。为方便研究,根据已有关于静电分离的文献[20],做出以下假设:金银花与编织袋丝等效为球体颗粒。物料之间不存在干扰。受到的镜像力恒定,不随位置的改变产生耗散。忽略吸附时摩擦阻力的影响。

如图1所示,作用在颗粒上的力包括镜像力Fi、重力Fg、离心力Fc以及空气阻力Fd。

图1 受力分析示意图Fig.1 Diagram of force analysis

物料的电荷量Q与电场强度E成正比[21],即

(1)

式中ε0——真空介电常数,F/m

εr——物料介电常数,F/m

rs——物料的等效半径,m

镜像力Fi将电场中的物料吸附于辊筒表面,与Q的平方成比例,即

(2)

Fg为物料所受重力,有

Fg=mg

(3)

式中m——物料质量,kg

g——重力加速度,m/s2

物料随着辊筒转动时受到的离心力Fc为

(4)

式中n——辊筒转速,r/min

R——辊筒半径,m

物料所受到的空气阻力Fd为

(5)

式中Ap——物料投影面积,m2

v——物料速度,m/s

Cd——阻力系数

ρ——空气密度,kg/m3

其中空气阻力经计算,约为10-7N,相比于其他力可以忽略。

金银花发生脱离的位置通常在辊筒右侧,按照金银花充电情况的不同,可分为两种脱离情况。第1种情况:金银花由于充电不足,受到向心方向的镜像力不足以克服重力、离心力和向前的惯性;此时金银花在辊筒右上侧脱落。第2种情况:金银花充电充分,受到镜像力较大,因此被吸附在辊筒表面,并随着辊筒转动,到达辊筒右下侧区域;在辊筒右下侧区域时,随着辊筒的转动,重力的影响不断加大;当金银花受到的镜像力小于重力和离心力的合力时,金银花脱离辊筒表面。由于第1种脱离情况对除杂效果影响较小,因此着重分析第2种情况。

如图2所示,可以看出,当金银花到达辊筒底部时,重力在竖直方向的分量达到最大,而镜像力和离心力的大小是不变的。因此该位置为金银花的临界脱离点,此时金银花的临界脱离条件可表示为

图2 金银花受力示意图Fig.2 Schematic of force of honeysuckle

Fi≤Fg+Fc

(6)

将各力的表达式代入式(6),可得

(7)

如图3所示,在除杂过程中,编织袋丝被镜像力吸附在辊筒表面,随着辊筒转动,最终被辊筒左侧的毛刷刷下。在此过程中,当编织袋丝位于辊筒底部时最容易脱离辊筒,因此该点为编织袋丝的脱落临界点。为满足编织袋丝全程不脱离辊筒,需满足条件

图3 编织袋丝受力示意图Fig.3 Schematic of force of woven bag filament

Fi≥Fg+Fc

(8)

由此可得辊筒临界脱离转速n1应满足的条件为

(9)

编织袋丝受到的镜像力与获得的最大荷电量有关。为了确保荷电量达到最大,应满足足够的充电时间,即满足辊筒转速不高于临界充电转速n2。n2计算式为[22]

(10)

式中k——离子迁移率,m2/(V·s)

q——空间电荷密度,C/m3

e——电晕荷电区域的宽度,m

综上所述,静电分离技术可用于金银花与编织袋丝的分离,但对于电场强度和辊筒转速,需满足相应的条件。在分离过程中,应保持辊筒转速不高于临界脱离转速和临界充电转速,以确保编织袋丝顺利去除。同时电场强度的增大可以提高编织袋丝的分离效果,但也不能过大,避免金银花越过临界脱离点,造成误除。

为进一步验证静电分离技术用于金银花除杂的可行性,在特定参数下对位于临界脱离点即辊筒底部的金银花和编织袋丝进行受力计算与对比。计算所用的参数如表1所示,计算结果为:编织袋丝受到的镜像力、重力、离心力分别为3.85×10-5、2.96×10-5、3.02×10-6N;金银花受到的镜像力、重力、离心力分别为1.19×10-4、1.99×10-4、2.03×10-5N。

表1 计算参数Tab.1 Calculation parameters

在编织袋丝的运动过程中,镜像力占主导作用,使得编织袋丝吸附在辊筒表面。在金银花的运动过程中,重力与离心力的合力占主导作用,使得金银花脱离辊筒。编织袋丝与金银花之间存在明显的受力差异,验证了静电分离技术用于去除金银花中的编织袋丝具有一定的可行性。

1.2 工作原理

金银花静电除杂装置工作原理如图4所示。上料机构将混有编织袋丝的金银花传输到输送带上,使得物料能够均匀、持续地进入辊筒表面。金银花中的编织袋丝经电晕电极充电,进入静电极产生的电场中,从而受到了镜像力,黏附在辊筒表面。随着辊筒旋转,编织袋丝被毛刷刷落,落入左侧的杂质收集室。而金银花受到重力和离心力较大,克服镜像力后直接落入右侧的金银花收集室。

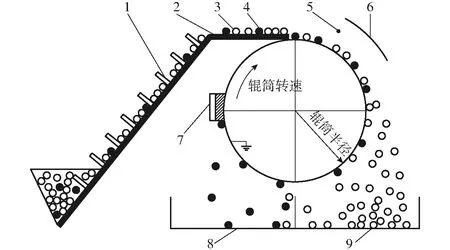
图4 金银花静电除杂装置原理图Fig.4 Schematic of electrostatic impurity removal device1.上料机构 2.输送带 3.金银花 4.编织袋丝 5.电晕电极 6.静电极 7.毛刷 8.杂质收集室 9.金银花收集室

1.3 整机结构设计

图5为金银花静电除杂装置结构示意图和实物图,金银花静电除杂装置主要包括上料机构、输送带、毛刷、辊筒、电晕电极、静电极、凹槽板、蝶形螺母、大带轮、传动带、小带轮、电机、电机支架、收集室和高压静电发生器。

图5 金银花静电除杂装置Fig.5 Honeysuckle electrostatic impurity removal device1.上料机构 2.输送带 3.毛刷 4.辊筒 5.电晕电极 6.静电极 7.凹槽板 8.蝶形螺母 9.大带轮 10.传动带 11.收集室 12.小带轮 13.电机 14.电机支架 15.高压静电发生器

1.4 关键部件设计

1.4.1辊筒设计

辊筒是静电除杂装置设计的关键,其结构参数对除杂性能有重要影响。通过查阅文献[23-25],静电除杂装置的辊筒直径选取范围通常为150～300 mm,增大辊筒直径,有利于使编织袋丝充分带电,从而提高除杂性能,但会增大所需要的电压值。综合考虑,设计辊筒直径为250 mm。辊筒采用不锈钢材质,辊筒空心且表面光滑有利于将编织袋丝吸附,辊筒长240 mm,厚度2 mm,两侧轴径为26 mm。

1.4.2电晕电极设计

电晕电极由直径为0.25 mm的铜线组成。为了确保辊筒表面的物料均能通过电晕电极带电,其长度需大于辊筒的长度,因此电晕电极的长度取250 mm。电晕电极位于静电极前端,使得物料提前带电。依据文献[26-28],电晕电极与静电极的距离选取范围通常为10～40 mm,距离大有利于物料充电,但同时容易引起火花放电,造成静电发生器损坏。综合考虑,电晕电极与静电极的距离选取为20 mm。

1.4.3静电极设计

静电极与高压静电发生器相连接,为除杂过程提供了稳定的电场区域。不同静电极形状会影响电场分布情况[29-30],因此本文选用3种静电极,截面形状分别为圆弧形、长方形和圆形,尺寸参数如图6所示。为了确保辊筒处于电场区域中,其长度需大于辊筒的长度,因此静电极的长度取250 mm。

图6 静电极尺寸参数示意图Fig.6 Schematic of electrostatic electrode size parameters

2 仿真与试验设计

2.1 仿真条件设置

电场是影响镜像力的关键因素,因此可通过仿真分析电极结构以及电压对电场的影响,进而分析对除杂效果的影响。本文基于COMSOL软件对静电除杂装置进行仿真,探究影响静电除杂装置电场的关键因素,确定最佳结构参数,为后续试验提供有力的理论支持。为了简化模型,降低仿真的复杂程度,做以下假设:空气的介电常数恒定且不受电场的影响。忽略带电的编织袋丝与金银花对整个装置的电场分布影响。忽略空气湿度、温度等外部环境对电场的影响。

图7a显示了简化后的静电除杂装置二维模型。二维模型由电晕电极、静电极以及辊筒组成。U为高压静电发生器的输出电压,L为静电极与辊筒的间距,α为静电极角度。通过改变以上参数进行仿真。在仿真过程中,辊筒的直径为250 mm,电晕电极的直径为0.25 mm。采用非结构化网格,最大单元尺寸设置为31.8 mm, 最小单元尺寸设置为0.18 mm, 最大单元生长率设置为1.3, 曲率因子设置为0.3,狭窄区域分辨率设置为1。模型的网格划分如图7b。长方形表示仿真边界,边长分别为600、500 mm。选用AC/DC物理场的静电模块进行场强分析,求解问题选为稳态。研究区域的电场强度为

图7 用于仿真的几何模型和网格Fig.7 Geometric model and meshes for electric field simulation1.辊筒 2.电晕电极 3.静电极

(11)

式中V——电势, V

静电除杂装置的有效电场区域如图8所示。图中黄色区域即为实现分离编织袋丝与金银花的有效电场区域。为了更加直观地观察辊筒表面的电场强度,定义辊筒表面任一点与辊筒中心的连线与水平线的夹角为θ,θ的取值范围为0°～90°。

图8 有效电场区域示意图Fig.8 Diagram of effective electric field areas

2.2 单因素样机试验设计

为合理选取影响除杂性能的关键因素及其取值范围,以静电极形状、高压静电发生器的输出电压U、辊筒转速N、辊筒与静电极的间距L、静电极角度α为试验因素,除杂率、误除率为试验指标,对金银花静电除杂装置样机开展单因素试验。本试验采用金银花3号品种作为试验对象,该品种外观近似棒状,长20～30 mm,平均直径2.5 mm,平均质量约为2.03×10-2g。所使用的编织袋丝长30～40 mm,平均质量约为3.02×10-3g。本试验选取的物料如图9所示。

图9 金银花与编织袋丝Fig.9 Honeysuckles and woven bag filament

试验环境温度为20℃,环境相对湿度为40%。通过调研,在每100 g的金银花中加入编织袋丝1.5 g, 混合均匀后的混合物在金银花静电除杂装置上进行分离试验,测定除杂率以及误除率。每组试验重复3次,取3次试验的平均值作为试验结果。单因素试验的参数水平如表2所示。

表2 单因素试验水平Tab.2 Single factor experiment factors levels

除杂率H以及误除率W计算式为

(12)

(13)

式中mg——金银花收集室中的编织袋丝质量,g

ms——编织袋丝总质量,g

mm——金银花总质量,g

mn——杂质收集室中金银花质量,g

2.3 Box-Behnken样机试验设计

为寻找使得静电除杂装置具有最佳工作性能的因素组合,基于仿真与单因素试验的结果,采用Box-Behnken试验法,以高压静电发生器的输出电压A、辊筒与静电极的间距B以及辊筒转速C为试验因素,除杂率Y1、误除率Y2为响应值,各试验因素编码如表3所示,试验方案与结果如表4所示。

表3 试验因素编码Tab.3 Coding of experiment factors

表4 试验方案与结果Tab.4 Experiment design and results

3 结果与分析

3.1 样机吸附试验

为探究金银花和编织袋丝被吸附的参数条件,以输出电压U为试验因素,吸附率为试验指标,开展单种物料的吸附试验。选择静电极与辊筒的间距L作为对照变量,取值分别为50 mm和70 mm。其余参数选择为:N=27 r/min、α=45°、静电极形状为圆弧形。每组选取20根金银花或编织袋丝进行试验,重复试验3次。当被吸附的金银花或编织袋丝到达辊筒左部,则视为吸附成功,计入吸附率的计算。试验结果如图10所示。

图10 吸附试验结果Fig.10 Adsorption test results

如图10a所示,当L为50、70 mm,编织袋丝刚好被吸附起的临界电压分别为10、14 kV。由图10b可知,当U<18 kV,金银花的吸附率维持一个较低水平。由于高电压情况下出现火花放电现象,未能完成L=50 mm、U>20 kV以及L=70 mm、U>24 kV时的金银花吸附试验,金银花的临界吸附电压需在后续研究中进一步探究。

3.2 仿真与单因素样机试验

3.2.1静电极形状

当电压为14 kV,转速为27 r/min,间距为60 mm,静电极角度为45°,静电极形状分别为圆弧形、长方形、圆形时,仿真与试验结果分别如图11、12所示。图11a显示了静电极下的电场分布情况,圆形静电极产生的电场区域的范围以及强度最小,圆弧形静电极产生的电场区域的范围以及强度最大。图11b显示了辊筒表面的电场强度,3种静电极下的电场强度均呈先增大后减小的趋势。电晕电极比静电极更加靠近辊筒,因此电场峰值均出现在θ=55°附近,即接近电晕电极的位置。圆弧形电极因其外凸的弧形结构,比长方形和圆形电极更加贴合辊筒表面,所产生的电场分布更均匀,电场强度也更大。因此在圆弧形静电极下编织袋丝受到的镜像力更大,有利于编织袋丝的去除。

图11 不同静电极形状下仿真结果Fig.11 Simulation results with different electrostatic electrode shapes

图12显示了不同静电极形状下的除杂率和误除率。由图可知,当静电极为圆弧形时,除杂率为95.6%,误除率为1.05%;当静电极为长方形时,除杂率为84%,误除率为0.98%;当静电极为圆形时,除杂率为60%,误除率为0.65%。试验结果表明,圆弧形静电极与其他两种静电极相比,除杂性能更佳,因此后续试验中静电极确定为圆弧形。

图12 不同静电极形状下试验结果Fig.12 Experimental results with different electrostatic electrode shapes

3.2.2电压

当转速为27 r/min,间距为60 mm,静电极角度为45°,电压分别为6、10、14、18、22 kV时,仿真与试验结果分别如图13、14所示。图13a显示了电场分布的情况,随着电压的增大,电场区域的范围以及强度均逐渐增大。图13b为辊筒表面的电场强度分布,由图可知,随着电压的增大,辊筒表面的电场强度逐渐增大。电场区域的范围越大以及电场强度越大越有利于辊筒表面的编织袋丝和金银花的镜像力增大。但当电压过小时,镜像力不足以吸附编织袋丝,导致除杂效果不佳;当电压过大时,部分较轻的金银花也被吸附。因此在实际应用中,不可以无限提高电压。

图13 不同电压下仿真结果Fig.13 Simulation results with different voltages

图14显示了不同电压下的除杂率和误除率。由图可知,当电压小于10 kV时,随着电压的增大,除杂率显著增大,误除率缓慢增加。电压越大,编织袋丝与金银花受到的镜像力越大,除杂率越高,同时误除率也缓慢增加。当电压大于14 kV时,除杂率逐渐趋于稳定,误除率显著增加。此时编织袋丝达到了充电临界值,继续增大电压,最大荷电量也不会发生明显变化,因此镜像力的变化趋于稳定。而金银花在电压14～18 kV的变化过程中,逐渐达到充电临界值,受到的镜像力显著增加,导致了误除率的激增。综上,在一定程度内,通过增加电压,可以有效提高除杂性能。而电压超出一定范围后,增加电压,误除率会显著提高。因此需要选择合理的电压参数,来考虑电压对除杂率和误除率的影响。根据仿真与试验结果,确定后续试验的电压取值范围为10～14 kV。

图14 不同电压下试验结果Fig.14 Experimental results with different voltages

3.2.3间距

当电压为14 kV,转速为27 r/min,静电极角度为45°,间距分别为50、60、70、80、90 mm时,仿真与试验的结果分别如图15、16所示。图15a显示了电场分布的情况,随着间距的增大,电场区域的范围逐渐增大,但强度逐渐减小。图15b为辊筒表面的电场强度分布。由图可知,在各间距下辊筒表面的电场强度均呈现中间大两边小的趋势分布,且随着间距的减小,电场强度逐渐增大。当间距为50 mm时,电场强度显著增大。当电晕电极与辊筒的间距过小,会使得电极间的电场等势面密度过大,从而导致该区域的电场强度剧增。仿真结果表明,间距减小会造成电场区域的范围缩小,但所产生的电场区域仍在有效除杂范围内,并且电场强度显著增强。

图15 不同间距下仿真结果Fig.15 Simulation results with different spacings

图16为不同间距下的除杂率以及误除率。由图可知,随着间距的减小,除杂率呈逐渐增大的趋势。当间距大于60 mm时,随着间距的增大,误除率逐渐降低。当间距为50 mm时,误除率剧增,这是因为此时产生的镜像力达到将金银花吸附于辊筒表面的临界值。此外在试验过程中发现,当间距取值小于50 mm时,出现了火花放电现象,不利于除杂。因此根据仿真与试验结果,确定后续试验间距取值范围为50～70 mm。

图16 不同间距下的试验结果Fig.16 Experimental results with different spacings

3.2.4静电极角度

当电压为14 kV,转速为27 r/min,间距为60 mm,静电极角度分别为25°、35°、45°、55°、65°时,仿真与试验的结果分别如图17、18所示。图17a显示了电场分布的情况,随着静电极角度的增大,有效电场区域内的电场范围以及强度先增大后减小。图17b为辊筒表面的电场强度。当静电极角度α=65°,电场强度率先达到峰值,随后进入下降趋势。当静电极角度α=25°,电场强度呈上升趋势,相比于其他的角度最晚到达峰值。电极角度决定了电场强度的分布,这影响到编织袋丝的充电质量,当α过大或过小时,编织袋丝在强电场区域中停留的时间较短,荷电量未能达到最大值,因此受到的镜像力较小。静电极在选择静电极角度时,应使得有效电场区域内的平均电场强度尽可能大。

图18为不同静电极角度下的除杂率以及误除率。由图可知,随着静电极角度的增大,除杂率呈现先增大后减小的趋势,误除率呈现逐渐减小的趋势。α=45°时,除杂率达到峰值。这说明该角度下有效电场区域内的平均电场强度达到了最大,编织袋丝充电充足,产生了更大的镜像力,因此实现更好的编织袋丝分离效果。而当α>45°或α<45°时,平均电场强度不同程度的减小,导致了除杂率的降低。此外,由于金银花的分离点主要集中于辊筒右侧中部,α越大,意味着金银花在分离点前未能充分充电,金银花受到的镜像力较小,导致误除率降低。综上所述,为满足最优的除杂效果,在后续试验中选择静电极角度为45°。

图18 不同静电极角度下试验结果Fig.18 Experimental results with different electrostatic electrode angles

3.2.5辊筒转速

当电压为14 kV,间距为60 mm,静电极角度为45°,转速分别为9、18、27、36、45 r/min时,试验的结果如图19所示。随着转速的提高,除杂率和误除率呈下降趋势。由前文的理论分析可知,编织袋丝要达到最好的分离效果,应使得转速不高于临界脱离转速和临界充电转速。当转速大于27 r/min时,除杂率由平稳趋势转为下降趋势。说明该转速附近出现了临界脱离转速和临界充电转速,当越过临界转速,编织袋丝受到的镜像力将减小,而离心力增大,因此除杂率急剧下降。对于金银花,转速的提高有利于减小充电时间,提高离心力,因此误除率降低。为进一步确定辊筒的最佳工作转速,选择后续试验的转速范围为18～36 r/min。

图19 不同转速下试验结果Fig.19 Experimental results with different roller speeds

综上所述,静电极形状、静电极角度、间距以及电压都会影响到有效电场区域内电场强度的分布和大小,进而影响到除杂装置的除杂率和误除率。而辊筒转速直接影响到镜像力和离心力,导致除杂率和误除率发生变化。

3.3 Box-Behnken样机试验

为进一步分析各因素以及因素间交互作用对试验指标的影响,本文应用Design-Expert软件对试验数据进行多元回归拟合,显著性检验结果如表5所示。

Y1=-242.315+37.235A+1.8195B+4.065C+
0.072 5AB-1.577 5A2-0.026 6B2-0.079 136C2

(14)

Y2=22.741 75-1.795 75A-0.340 40B-0.090 5C-
2.875×10-3AB-3.472 22×10-3AC+0.103 94A2+
2.657 5×10-3B2+1.675 93×10-3C2

(15)

表5 响应面试验方差分析Tab.5 Variance analysis of response surface model

由表5可知,除杂率Y1和误除率Y2的二次回归模型均达到极显著水平(P<0.01),失拟项均为不显著(P>0.05)。R2分别为0.991 7、0.998 5,表明模型精度较高,回归方程与数据拟合较好。因此,可用该模型对除杂性能指标进行预测。在回归模型Y1中,回归项A、B、C、A2、B2、C2对Y1影响极显著(P<0.01),回归项AB对Y1影响显著(P<0.05),AC、BC对Y1影响不显著。在回归模型Y2中,回归项A、B、C、A2、B2、C2对Y2影响极显著(P<0.01),AB、AC对Y2影响显著(P<0.05),BC对Y2影响不显著。影响除杂率的主次因素顺序为:高压静电发生器的输出电压、辊筒与静电极的间距、辊筒转速;影响误除率的主次因素顺序为:高压静电发生器的输出电压、辊筒与静电极的间距、辊筒转速。

将表5中回归模型不显著项剔除,保证模型极显著、失拟项不显著,重新拟合得到试验指标Y1、Y2的预测数学模型分别为

图20为因素之间的交互作用对除杂率影响的响应曲面图。当转速为27 r/min,电压为10 kV时,随着间距的减小,除杂率逐渐增大;当转速为27 r/min,电压为14 kV时,随着间距的减小,除杂率先增大后趋于稳定。

图20 因素交互作用对除杂率影响的响应曲面Fig.20 Response surface plots of each factor on impurity removal rate

图21为因素之间的交互作用对误除率影响的响应曲面图。如图21a,当转速为27 r/min,电压一定时,误除率随着间距的增大而减小;当电压较小,间距较大时,可获得较小的误除率。如图21b,当间距为60 mm,转速一定时,误除率随着电压的减小而减小;当电压较小,转速较大时,可获得较小的误除率。

图21 因素交互作用对误除率影响的响应曲面Fig.21 Response surface plots of each factor on false removal rate

为准确获得各因素的最优参数组合,以最大除杂率和最小误除率为最终优化目标,结合边界条件,建立的二次回归模型为多因素优化解,其目标函数及约束条件为

(16)

采用Design-Expert对该方案进行优化,得到最优参数组合为:电压11.9 kV、转速28 r/min、间距60 mm,在该参数组合下除杂率为94.19%、误除率为0.79%。在相同条件下进行验证试验,得到除杂率与误除率分别为94.47%和0.89%,与预测值相比误差较小。

4 结论

(1)通过理论分析,确定了金银花与编织袋丝产生轨迹分离的临界条件。辊筒转速不宜大于临界脱离转速和临界充电转速,否则会导致编织袋丝的充电不足以及离心力的增大。基于特定参数下的计算,说明了金银花与编织袋丝由于介电性能和质量的不同会出现明显的受力差异,进一步验证了静电分离技术用于去除金银花中编织袋丝的可行性。

(2)静电极形状和角度改变了有效电场区域内的电场分布和平均电场强度,从而影响到金银花与编织袋丝受到的镜像力,导致除杂率和误除率发生改变。通过单因素试验和仿真确定了静电极的最优形状为圆弧形,最优角度为45°。在此参数下,有效区域内的平均电场强度达到最大值,编织袋丝能够充分充电,有利于编织袋丝的分离。

(3)采用响应面分析法,分别建立了除杂率和误除率的二次回归方程。多目标优化结果表明,当电压为11.9 kV、转速为28 r/min以及间距为60 mm时,除杂效果最佳,在此条件下进行了台架验证试验,得到除杂率与误除率分别为94.47%和0.89%,与预测值相比误差较小,优化后的静电除杂装置性能满足金银花除杂的技术要求。