基于机理分析的草原放牧策略研究
于和硕
(上海理工大学机械工程学院,上海 200093)
0 引言
在草原放牧的过程中,通常需要考虑两个因素,分别是放牧方式和放牧强度。放牧方式和放牧强度选择的不同,结果也会不同。植物的生长除了受自身生长规律的影响外,还有外界刺激的影响。当牧羊采食牧草时,地上的生物量会减少,同时,植物有着超补偿生长的特点,适当放牧有利于植物的生长,进而改善土壤质量,而过度放牧则会导致植被破坏,增大土地裸露面积,甚至导致土壤板结化、土地沙漠化,使得土壤肥力下降,危害环境。
内蒙古锡林郭勒草原是国家最重要的畜牧业产业基地之一,也是北方绿色生态走廊。因此,为锡林郭勒草原构建一个基于放牧策略对环境影响关系的模型对于保护其环境生态系统具有重要的意义。
1 样本数据处理
近年来,科研工作者在内蒙古自治区锡林郭勒盟草原上选取代表性草场进行了大量的实验,采集了不同牧户生态畜牧业模式群落样方调查数据以及不同示范牧户牲畜数量调查数据;还有不同放牧强度土壤碳氮监测数据、轮牧放牧样地群落结构监测数据。
基于这些数据,首先从计算的角度,对公式进行分析和推导,建立微分方程,分析内部机理。然后进行数据挖掘,对数据预处理如描述性统计分析,采用单因素方差分析确定放牧策略对土壤有机物含量均值的影响。
1.1 放牧策略与植被生物量的数学模型
对于放牧与植物生长之间的关系,Woodward 等建立了如下一个简单模型[1]:
其中,w为植被生物量,S为单位面积的载畜率。
查阅相关文献所给的土壤—植被—大气系统的水平衡基本方程[2-5]:
其中,ΔW 为土壤贮水变化量,Wt+1和Wt分别为时间段内的始末土壤含水量,P为降水量,Gu和Gd分别为地下水毛管上升量和土壤水渗透量,Eta为实际蒸发量,Rin和Rout分别为入和出径流量,ICstore为植被截流量,其表达式为:
其中,cp为植被覆盖率,ICmax为特定植被的最大截流量(mm),k 为植被密度校正因子,与LAI 有关,Rcum为累积降雨量(mm)。ICmax可以通过LAI来估算:
其中,LAI为一个分布式的时变参数。根据研究表明,当地下水埋深度大于4m 后,毛管上升水对2m 土壤水分循环的作用很小。草原地下水埋藏较深,地下水毛管上升量对根系层的补给量也可忽略,则有Wt=W0,故⑵式简化为式⑸[4]:
植被覆盖率的公式如下:
式⑴~式⑹,即是生物量与放牧策略之间的关系。
1.2 放牧策略与土壤物理性质的数学模型
植被截流量表达式为:
其中,牧区供水率(主要为降水)为P;地表蒸散发率为E;土壤含水量为β;土壤植被覆盖率为α*G(w);成草数量为w;草原的盖度为G(w)=(1-e-εgw/w*);枯萎率为D=β*(eεgw/w*-1),其中w*是该草原群落的特征值。对式⑺积分可得式⑻:
式⑻即为放牧策略与土壤物理性质之间的关系。
1.3 数据统计分析
根据上述所示的模型,进行数据驱动的机理分析。根据提供的数据,计算不同的放牧策略对土壤有机物含量均值的影响。土壤有机物含量均值如表1所示。
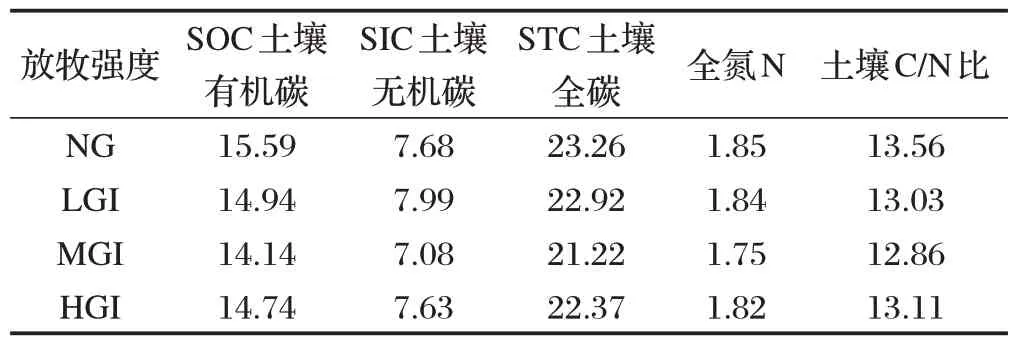
表1 不同的放牧策略对土壤有机物含量均值的影响
根据表1 可以看出,土壤有机物含量的均值差异可能与放牧策略的不同有关。要探究不同的放牧策略是如何对土壤有机物含量的影响,我们要做一下单因素方差检验,看一下究竟是否存在显著差异。
分析具体步骤不详细展开,分别对不同放牧强度中的SOC 土壤有机碳、SIC 土壤无机碳、STC 土壤全碳、全氮N以及土壤C/N比进行平均值检验,检验结果如表2所示。

表2 不同的放牧策略对土壤有机物含量均值的影响
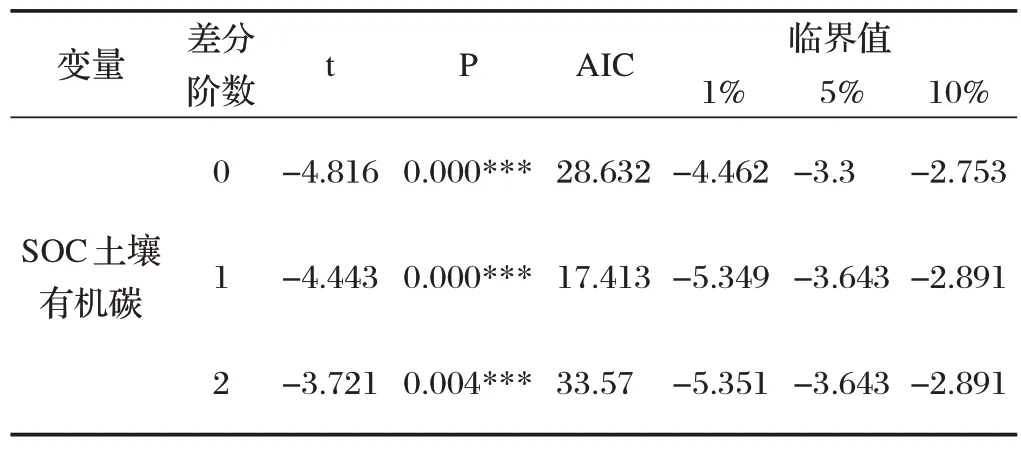
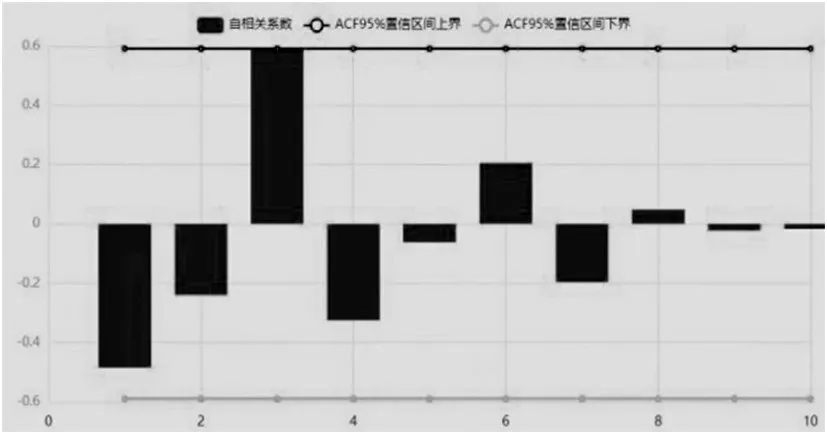
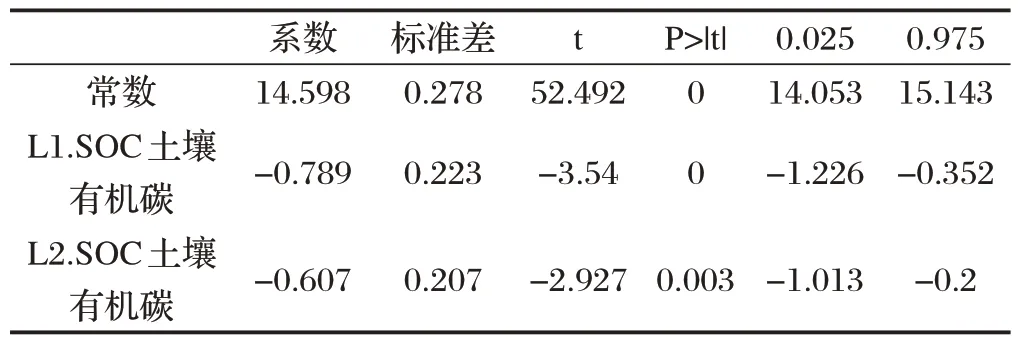
根据表2 可以得到对于SOC 土壤有机碳、SIC 土壤无机碳、STC土壤全碳、全氮N以及土壤C/N 比这五个变量,四种放牧强度的均值大小排序:①对于SOC土壤有机碳,对放牧强度进行排序可以得出:MGI 综上所述,得出了放牧强度与土地化学性质之间的影响关系,并对其显著性进行判断,发现对于STC土壤全碳,HGI 和MGI 存在显著性差异,其他情况下并不存在显著性差异。 ARIMA模型全称是自回归移动平均模型,是统计模型中一种流行且广泛使用的时间序列预测统计方法,可记为ARIMA(p,d,q)。 其中AR 是“自回归”,p代表预测模型中采用的时序数据本身的滞后数(lags);MA为“滑动平均”;q代表预测模型中采用的预测误差的滞后数(lags) ;d 代表时序数据需要进行几阶差分化[6]。模型的一般形式如式⑼表示: ARIMA时间序列模型的建立主要有以下三个过程: ⑴序列判断 首先需要对数据进行判断,确定需要建立的模型数据是否是平稳序列,若P<0.05,则说明时间序列平稳,如果序列不平稳,要对数据做预处理。 ⑵模型估计与建立 当自回归模型被成功建立后,为了得到最优的模型结构,需要对p 和q 的值进行确定,可以通过自相关系数ACF和偏自相关系数PACF决定。 ⑶模型诊断 对模型参数的显著性进行判断,如果模型诊断合格,则可以说明模型设定正确,可以进行最终的预测。 ⑴检验ADF 确定模型数据是否是平稳序列,对数据ADF 检验,其结果如表3所示。 表3 ADF检验表 上表序列检验的结果说明,在差分阶数是0、1、2阶时,该序列是平稳的时间序列,故可进行下一步求解。 ⑵定阶 为了确定模型的最优结构,对p 和q 的值进行确定,其中自相关系数ACF 图与偏自相关系数PACF 图如图1、图2所示。 图1 自相关系数ACF图 图2 偏自相关系数PACF图 ⑶模型评价与参数确定 将数据带入模型进行检验,结果如表4所示。 表4 ARIMA模型检验表 从表4 可得,拟合优度R2为0.724,可知模型表现较好,模型基本满足要求。 经过模型拟合后的参数如表5所示。 表5 ARIMA模型参数表 以SOC 土壤有机碳为自变量,模型基于AIC 信息准则自动寻找到最优参数后,可建立模型公式如下: 其中,t为预测时间。 ⑷预测结果 根据建立的模型对2022年的数据进行预测,时间序列图如图3所示。 图3 时间序列图 2022 年预测结果为13.510(结果保留三位有效数字),即在放牧强度为HGI,放牧小区为G9 的条件下,SOC 土壤有机碳含量为13.510。同理,按照上述方法依次对其他数据进行拟合,最终可以得到的预测表,如表6所示。 表6 预测结果 从机理分析的角度,建立放牧策略与草原土壤化学性质关系的数学模型,同时结合数据,采用单因素方差分析模型对放牧策略与草原土壤化学性质关系进行定量分析。发现对于STC 土壤全碳,HGI 和MGI存在显著性差异,其他情况下并不存在显著性差异。最后利用ARIMA 模型完成了2022年土壤中化学成分进行预测,预测结果为13.510(结果保留三位有效数字),即在放牧强度为HGI,放牧小区为G9 的条件下,SOC土壤有机碳含量为13.510。其余结果见表6。2 ARIMA时间序列模型的建立
3 结果预测


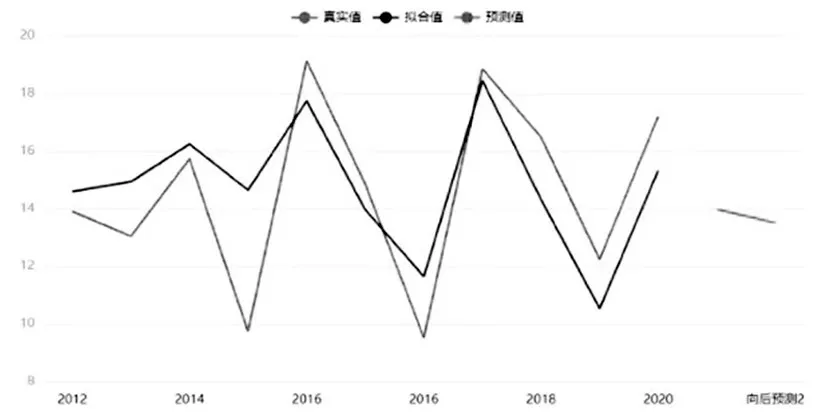

4 结束语

