水浮式大蒜鳞芽调整机构的设计与仿真

张光辉 ， 段志超 ， 隋荣娟 ， 孙 光

（1.山东交通学院工程机械学院，山东 济南 250357；2.山东交通学院航运学院，山东 济南 250357）

0 引言

目前，大蒜鳞芽调整主要采用机械结构、机器视觉、红外检测识别以及液力等方法。机械方面主要有双鸭嘴式[1]、锥形矫正碗[2]、仿形换向器[3]等结构。机器视觉是根据大蒜头尾不同的纹理特征，采用图像识别技术，识别蒜种鳞芽方向[4]，再基于卷积神经网络（CNN）和支持向量机（SVM）分类优化的改进算法（CNN-SVM），实现大蒜鳞芽朝向的自动识别与修正[5]。例如，采用双卷积神经网络模型结构，基于Jetson Nano 处理器的大蒜鳞芽朝向自动调整装置[6]。栗晓宇[7]设计了智能蒜种定向装置，通过红外传感器检测大蒜鳞芽朝向。液力调姿的原理是蒜种在水中时，由于自身重力和浮力的作用，使其尾部朝下[8]。为分析影响大蒜鳞芽调整的因素，张立娟[9]、文恩杨[10]对大蒜鳞芽调整机构进行了仿真。数值仿真成本低，仿真结果可视化程度高，可大大提高设计效率和效果。

采用机械结构进行调整时，容易对大蒜造成损伤；利用算法识别大蒜鳞芽成本较高，而且限于蒜种的尺寸不一、形态各异，识别结果会存在一定偏差。与其他方法相比，液力调整受力柔和、正芽率高。基于此，本文利用大蒜所受浮力与自身重力设计了一款大蒜鳞芽调整装置，既解决了蒜芽定向问题，又使得设备结构简单、成本低。

1 大蒜尺寸及鳞芽调整原理

本文以山东金乡大蒜为例，取50 组大蒜作为测量样本，采用游标卡尺与电子天平分别测量大蒜尺寸和质量，通过量筒测量大蒜体积，将各数据的平均值作为最终测量结果。大蒜长、宽、高如图1 所示，测量结果如表1所示。

表1 大蒜测量数据

图1 大蒜外形尺寸及受力示意图

通过悬挂法测量大蒜长度、宽度方向上的重心位置。经过多次测量发现，在鳞芽朝上的姿态下，大蒜的重心大约在距离底部1/3处，如图1所示。大蒜在水中受浮力与重力的作用，在刚落入水中时，浮力与重力不共线，两力形成的一对力偶矩导致大蒜发生翻转。当大蒜受力平衡时，重力与浮力共线，由于重心靠近根部，所以大蒜最终会呈现鳞芽斜向上的姿态。

2 大蒜鳞芽调整机构设计

大蒜鳞芽调整机构主要包括过水勺、传动系统、扶正斜面、水箱、扶正弹簧，如图2所示。

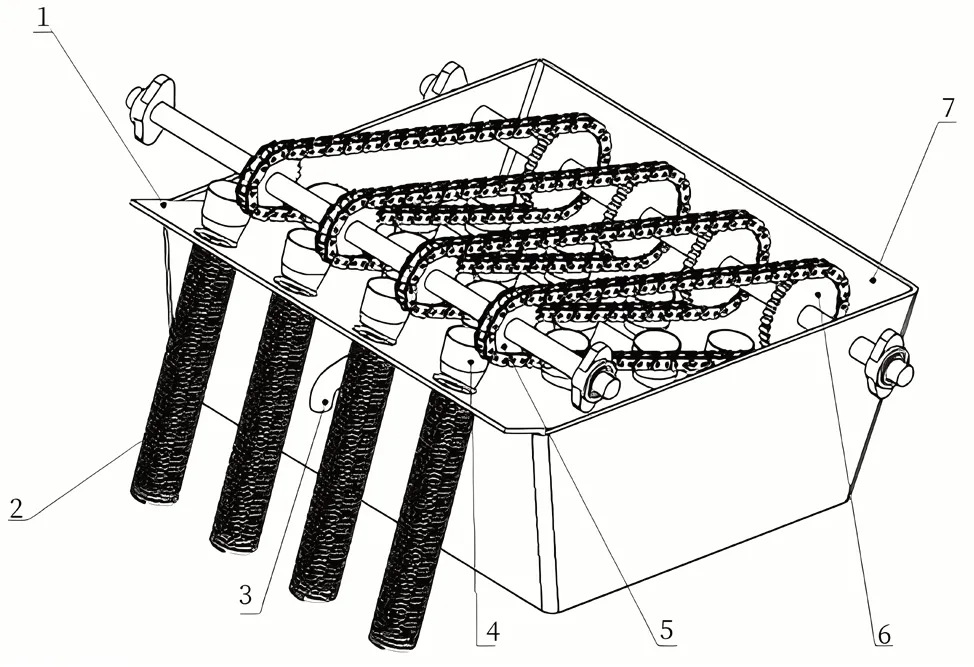
图2 鳞芽调整机构

过水勺的作用一是接收来自取种器的蒜种，保证单粒播种；二是和输送链一起将蒜种输送至扶正弹簧，蒜种在输送过程中完成姿态调整。如图3 所示，过水勺设计为类漏斗型，内部自上而下由三部分构成，第一部分为空心圆柱，大蒜在空心圆柱内会进行姿态调整，为保证大蒜以任意姿态落入过水勺，空心圆柱的直径需满足d1＞32.92 mm，取d1=45 mm。第二部分空心圆台上底面直径d2取35 mm。第三部分为上底面为斜面的空心圆台，底部椭圆短轴b需满足允许已经完成姿态调整的大蒜顺利落下，所以b＞20.11 mm，取为25 mm。过水勺高度h＞32.92 mm，取为50 mm。过水勺内部结构较陡，保证了蒜种进入底部之后不会再发生任何翻滚。为保证过水勺中的水量，需通过出水管控制水箱的水位。水箱内的扶正斜面，保证了大蒜在输送过程中不会从底部漏出，如图3 所示，扶正斜面的斜率需与过水勺底面的斜率相同。扶正斜面与水平面的夹角β取20°~30°。过水勺里的大蒜位置调整后进入扶正弹簧，长度取900 mm，直径不宜过大，同时要能够保证过水勺底部的蒜种顺利落入，直径取30 mm。

图3 过水勺剖面图

根据农业技术种子（穴）分布要求，每公顷播种的蒜种个数Ns为[11]：

式中，a为行距，m；ar为株距，m；M是每个穴中的种子数量。

当播种机前进速度为vm时，大蒜鳞芽调整机构输送蒜种的速度应为[12]：

装配式建筑的设计—加工—装配一体化技术………………………………… 卢保树，张波，张树辉，王东（9-18）

式中，v为输送蒜种的速度，m/s；vm为播种机前进速度，m/s。

把式（1）代入式（2）可得：

对于大蒜种植机械来说，每穴单粒种植，因此M=l，则大蒜鳞芽调整机构输送蒜种的速度为：

大蒜播种机作业速度较高时，性能显著下降，不能达到农业技术要求，播种机前进速度vm取2.6 km/h[12]。株距ar取130 mm，设两个过水勺之间的距离为Lm，那么大蒜鳞芽调整机构输送蒜种的实际速度v'是：

式中，Lm为两个过水勺之间的距离，m；vp为链条的输送速度，m/s。

根据大蒜播种机前进速度vm算出的输送蒜种的速度v应该与根据两个过水勺之间的距离Lm算出的实际速度v'相等，即：

则Lm=vpar/vm。当链条速度vp确定时，根据播种机前进速度vm，便能确定出过水勺之间的放置距离。链条带动过水勺取蒜的速度vp不应该太大，否则会影响取蒜的效果。对于大蒜鳞芽调整机构链条速度，试验表明，当链条速度为0.5 m/s 时，作业质量较好；当链条速度为0.55 m/s 时，作业质量虽然有所降低，但基本能满足农业技术要求；当速度高于0.55 m/s 时，作业质量会显著降低，漏播严重[11]。因此，大蒜鳞芽调整机构输送链条最高作业速度不超过0.5 m/s。大蒜播种机的最大前进速度取2.6 km/h，当前进速度低于2.6 km/h 时，vp<0.5 m/s。将vp≤0.5 m/s 代入式（6）可得Lm的值：

因此，两个过水勺之间的理论间距Lm≤90 mm。

为使输送链结构紧凑，寿命长，应尽量选用较小节距的单排链。选用滚子链08A，节距p=12.7 mm。进行圆整后，两个过水勺之间的实际距离，计算得n≤7.1，n取7，即两个过水勺之间的距离为7 个链节。输送链轮小链轮的齿数Z1不宜过少，一般Z1≥17[13]。小链轮齿数Z1取17。链条的线速度vp取0.5 m/s。把以上数据代入下式：

可得小链轮的转速n1=1 3 8 r/m i n。中心距ap=50p= 635 mm，传动比i取2[13]，则输送链轮大链轮的齿数Z2=iZ1=34，大链轮转速n2=69 r/min。

3 大蒜鳞芽调整过程仿真

3.1 模型的建立

利用SolidWorks建立大蒜三维模型，发现模型中大蒜的重心在(0.02,-9.02,-243.51)处，这与实验测量结果基本一致。令大蒜鳞芽朝下，大蒜底部距离水面高度100 mm，根据测量数据计算得到大蒜的密度为0.90 g/cm3。将模型导入到FLUENT，模拟大蒜在水中的调整过程。

3.2 网格划分

对流体域进行网格划分，采用四面体网格，图4展示了鳞芽朝下时流体域的网格划分结果，单元数为200 324、节点数为42 116。流体域长200 mm、宽250 mm、高550 mm。如图5（a）所示，蓝色网格部分为液态水，灰色网格部分为空气。大蒜位于空气域内部，如图5（b）所示。

图4 鳞芽朝下网格

图5 大蒜鳞牙朝下时流体域网格图

3.3 模型的选择

湍流模型采用R e a l i z a b l ek-e p s i l o n 模型，Realizablek-epsilon 模型的湍动能及其耗散率输运方程为[14]：

式中，k为湍流动能；ε为动能耗散率；Gk表示由于平均速度梯度引起的湍动能产生；Gb为浮力产生的湍流动能；YM为可压速湍流脉动膨胀对总的耗散率的影响。C1为模型常数；S为参数；μ、μt分别为层流、湍流黏性系数；xi、xj为沿x、y方向的坐标；ρ为气体密度。在FLUENT 中，C2和C1ε是常数，分别默认为1.9 和1.44；σk和σε分别是湍动能及其耗散率的湍流普朗特数，默认为1.0 和1.2。对于流动速度与重力方向相同的流动C3ε=1，对于流动方向与重力方向垂直的流动C3ε=0。

FLUENT 中处理多相流的模型有VOF 模型、混合模型、欧拉模型。VOF 模型是通过求解单独的动量方程和处理穿过区域的每一流体的体积分数来模拟两种或三种不能混合的流体。所以VOF 模型适用于计算空气和水这样不能互相掺混的流体流动。VOF 模型是根据各个时刻流体在网格单元中所占体积函数F来构造和追踪自由面的。若在某时刻网格单元中F=1，则说明该单元全部为指定相流体所占据，为流体单元；若F=0，则该单元全部为另一相流体所占据，相对于前相流体则称为空单元；当0

连续方程为：

式中，μi为i方向上的速度分量；ρm为混合物密度，ρm=(1-αq)ρl+αqρg，其中ρi(i=l,g)分别为水和空气的密度。

动量方程为：

式中，pm为混合物压强；μm为混合物动力黏性系数；μt为湍流黏性系数；μl紊动黏滞系数。

3.4 计算方法

压力-速度耦合采用coupled 算法，此算法是一种统一求解动量和基于压力的连续方程的隐式耦合算法。耦合控制方程中的每个方程要线化成一个涉及所有未知量的方程，通过离散动量方程中的压力梯度项以及耗散项实现求解[15]。

3.5 边界条件

将有大蒜的一端作为顶部，定义为压力出口，左右及底部边界定义为固定壁面，三维大蒜壁面定义为运动壁面，重力方向由计算域顶部指向底部，即大蒜自由落体的方向，重力加速度g=9.81 m/s2。忽略大蒜X、Y、Z三个方向的初始速度。

3.6 结果分析

大蒜距离水面的距离为100 mm，图6 为大蒜以鳞芽朝下姿态下落时的方向调整过程。从图中可以看出，在t=0.08 s 时，大蒜与水面接触，此时大蒜姿态与初始状态是一致的，由于重力大于浮力，大蒜继续向水中运动。大蒜在水中受力如图7 所示，处在液体中的物体，其浮心一般不与重心重合，浮心与重心的位置关系会影响物体在液体中的稳定程度，重心在浮心上面，则物体就处于不稳定状态；反之，当重心处于浮心下方时，物体则处于更加稳定的状态[14]。重力和浮力产生的力偶矩使大蒜整体发生顺时针旋转，如图7 所示。随着大蒜姿态的变化（如图6 所示），浮心位置也发生变化，直到t=0.35 s 时，浮心位于重力方向上，此时重力与浮力构成一对平衡力，大蒜位置调整过程到此结束。大蒜以鳞芽斜向上的姿态进入扶正弹簧管，使大蒜以鳞芽朝上的姿态进入播种器。

图6 大蒜距离水面100 mm，鳞芽朝上下落调整过程

图7 大蒜在水中受力图

4 结论

本文根据大蒜重力以及在水中受到的浮力，设计了水浮式的鳞芽调整机构，整体机构由过水勺、传动系统、水箱、扶正弹簧、扶正斜面构成，对大蒜鳞芽调整过程进行了有限元模拟。模拟结果表明，当大蒜距离水面100 mm 时，需要的调整时间为0.35 s，以大蒜鳞芽朝下落入水中为例，大蒜最终都会调整到鳞芽斜向上的姿态。在整个仿真过程中，大蒜在接触水面时开始受到浮力的作用，经过姿态调整后，重力与浮力共线，大蒜鳞芽斜向上。