农业机械金属波纹管液压成形数值模拟研究*

丁梦云 ，王 友

（湖北文理学院机械工程学院，湖北 襄阳 441053）

0 引言

金属波纹管是一种广泛应用于农业机械设备领域的重要元件。金属波纹管作为一种传动元件，可以用于传递动力和扭矩，同时也可以作为液压元件，用于传递液压油和控制液压系统。其次，金属波纹管还可以作为农业机械设备的排气管、进气管、冷却管等元件，用于排放废气、吸入新鲜空气和散热降温。相比于传统的橡胶软管和塑料软管，金属波纹管具有更高的耐压性、耐腐蚀性和耐高温性，可以承受更高的压力和温度，同时也更加耐久。此外，金属波纹管还具有良好的弹性和柔性，可以适应各种复杂的工作环境和工作条件，提高了农业机械设备的可靠性和稳定性。因此，金属波纹管在农业机械设备领域的应用前景广阔，具有重要的意义和价值。

近年来，管材液压成形这一技术广泛应用于研发中空零件装配[1]，在这种工艺下加工出来的波纹管在降低重量的同时还能保持材料的强度和刚度。波纹膨胀接头在当下热处理管网及设备的热补偿上作为关键的部件，它有着位移补偿、减少震动、降低噪声和密封[2]的优点。波纹管膨胀节包括端管、支架、法兰、导管及组成应用主体的波纹管等有关配件[3]。而液压成形是波纹管生产过程中最为普遍的一种生产工艺，但在生产过程中仍有一定的缺陷，如产品易开裂、产品质量受影响等，故有待改进。对于波纹管成品而言，想要应用在航天航空、汽车等产业上，不仅要做到质量轻，而且还要具有耐腐蚀、不易变形、能经受高温高压的工作环境等特点[4]。所以在波纹管液压成形过程中就应该要有严格的要求，在成形技术这一方面要有更深入的研究。

就管道的本构方程而言，林艳丽[5]显示了通过管两端的固定凸出模拟研究整理出的应力-应变曲线，发现只要凸出区域足够短，就更相似板的单轴拉伸曲线；此外，还有通过管两端的自由凸出测试获得的应力-应变曲线，发现只要凸出区域足够短，就更远离板的单轴拉伸曲线。从材料性能方面来看，林启权等[6]通过DYNAFORM 软件对板材在液压成形中存在的相关参数进行了模拟实验分析，获得了相关参数在管件液压成形过程中性能变化的影响情况。在性能参数上，管材液压成形中的内压和轴向进给十分重要。恰当地标定参数，能够防止各种缺陷形成。Yang 等[7]通过来自响应面和灵敏度研究的最佳方法找到最佳加载途径，约束完整出型的零件同模具内表面相关联系的配合度，以努力达到零件内外壁变化情况最小的结果，使负载路径由多个模拟确定。

本文利用ABAQUS/CAE 软件对金属波纹管的液压成形工艺进行了几何建模，采用有限元数值模拟的方法[8-10]，对各种工况下的管材液压成形工艺进行了仿真，证明了该模型的真实性和计算方法的准确性。

1 研究方案

1.1 管材介绍

本文采用ST14 钢，此钢材产自于德国，由于ST14 钢硬度高，且具有较强的塑性和良好的压力加工性，最终选择了ST14 钢作为实验管材。ST14 钢的密度为7 850 kg/m3，弹性模量为200 GPa，泊松比为0.28，该管材的真实应力-应变分布曲线如图1所示。

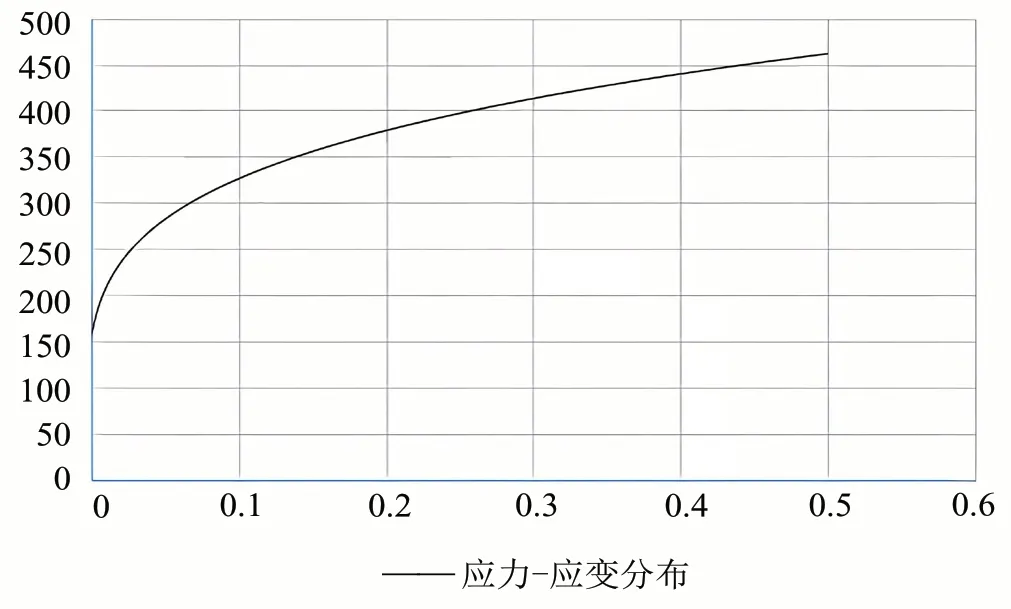
图1 应力-应变分布曲线

1.2 几何模型

采用ABAQUS/CAE 软件，对金属波纹管的液压成形工艺进行了几何建模，模型包括上模片、下模片、中间模片及管材。为提高运算速度和缩短运算时间，设定模具为解析刚体，管材为弹塑性模型。考虑整体模型的对称性，建立轴对称模型，如图2所示。

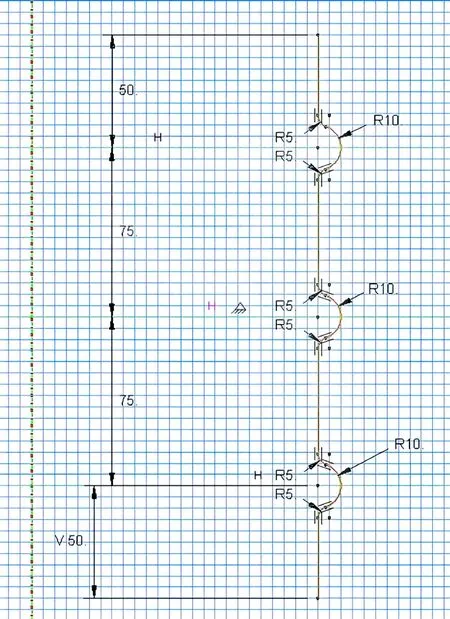
图2 轴对称模型

1.3 算法选择

在波纹管液压成形时，波纹管会产生塑性变形，如开裂、起皱，这样就导致了求解的不稳定性，从而使解不能收敛。而ABAQUS 软件中的Explicit 动力显式算法优势十分显著，其有着强大的接触功能分析方法，计算速度更快。因此，本文选用ABAQUS/Explicit 求解器对ST14 钢波纹管的液压成形过程进行仿真。

1.4 接触类型选择

有限元分析中的面面接触是针对每个从节点寻找从面的邻接面片，选取每个从节点邻接面片的样本点（如高斯点），利用N2S 法寻找对应的主面面片，确定主面面片之后，建立从面面片与主面面片间的多接触单元以及与多接触单元相对应的一个从面面片。而波纹管液压成形过程中以圆柱体金属管材为主，这时模型选用面面接触将使接触压力分布更均匀，使其后续计算结果比较准确。

当两个物体相互接触时，力会通过它们的接触表面进行传递。在特定情况下，只会在接触面垂直方向传递作用力，若有摩擦则作用力会沿着接触面切线方向传递切向力。本文从动力学角度出发研究了这一问题。结果表明：当接触压力较小时（小于等于0），摩擦力将产生于接触面；随着接触压力增大（大于0），摩擦力不再在界面处形成。接触的穿透和不穿透行为如图3 所示。管材和模具之间存在切向摩擦，由于润滑剂的作用，摩擦系数很小，假设其均匀润滑，通常摩擦系数取0.05~0.15，本文摩擦系数取0.05。当摩擦剪应力达到某个临界值时，会发生相对滑动。切向摩擦接触采用Penalty 法（罚函数法），罚函数方程为：

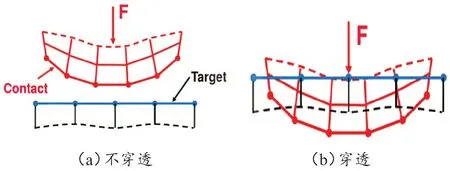
图3 接触不穿透与穿透

其中，Fn为接触力；kn为接触刚度；xp为穿透量。

2 波纹管液压成形的数值模拟

2.1 波纹管成形过程的应力分析

本节模拟了ST14 钢波纹管的液压成形过程，分析了管材在成形过程中的应力应变状态并将其与理论相比较，来验证有限元模型。通过5 次试算来确定管材成形所需的压强，如图4 所示。

图4 压强试算

观察管材变形过程发现：随着管材内部压力P的逐渐增大，管材轴向收缩（即管材变短）、管壁压入波纹凹槽，直至管壁与所有波纹凹槽完全贴合。可以看出，随着内部压力P的逐渐增大，管壁压入两侧波纹凹槽的变形程度要大于压入中间波纹凹槽的变形程度，这就意味着管壁首先与两侧的波纹凹槽贴合，然后再与中间的波纹凹槽贴合。可以将这个过程当作确定管材成形压力Pc的判定原则，即在模拟时，首先设定一个数值较大的压力P，然后依次观察两侧、中间波纹凹槽与管壁贴合时的压力，当管壁与中间波纹凹槽贴合时即认为此时的压力为管材的成形压力Pc。基于这个判定方法，通过观察发现，本案例（μ=0.05）的管材成形压力Pc=38.02 MPa。中间波纹凹槽的局部视图如图5所示。

图5 中间波纹凹槽的局部视图

为使分析结果更加直观，本文对轴对称模型进行了扫掠处理，得到的总体模型如图6所示。

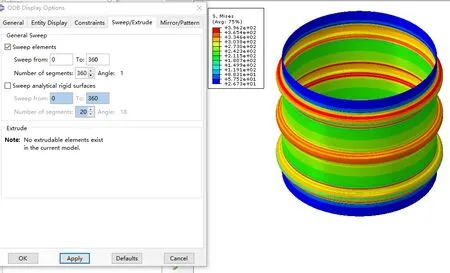
图6 扫掠处理后的模型

下面结合主应力分布，对管壁成形过程进行进一步分析。波纹凹槽处的Mises 应力分布如图7 所示。观察发现，管壁两端应力较小，只有几十兆帕；上部波纹凹槽和下部波纹凹槽处的管壁Mises 应力基本上呈对称分布；中间波纹凹槽处的管壁Mises 应力分布相对均匀且数值上整体更大。这是由于与两侧波纹凹槽处的管壁相比，中间波纹凹槽处的管壁最后贴合，其承受了一定程度的拉伸作用，因此在该区域的管壁的应力也相对较大。

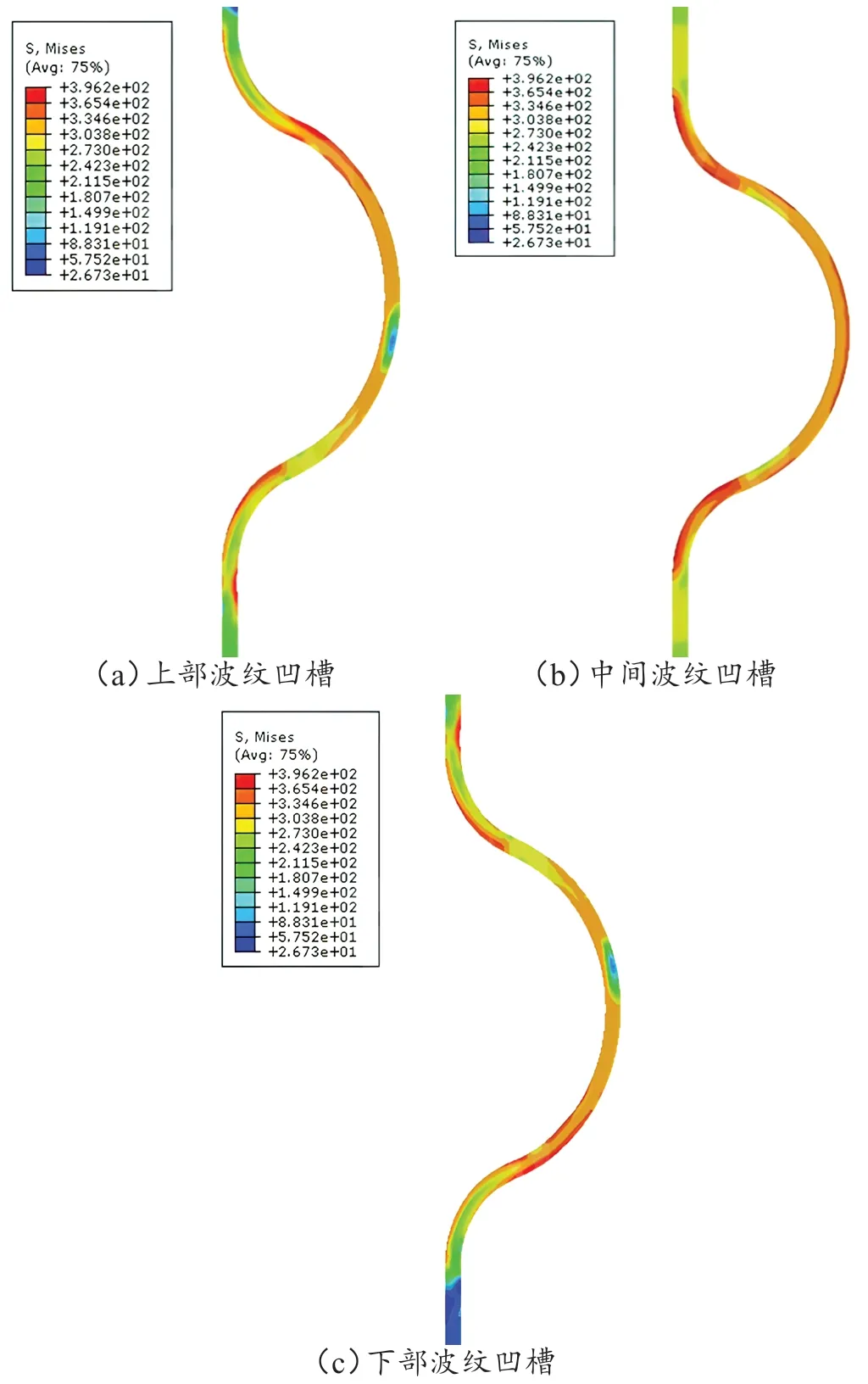
图7 波纹凹槽处的Mises应力分布云图

为定量研究管壁的变形特性，下面以主应力为对象对管材变形过程进行分析。波纹凹槽处的主应力分布如图8 所示。观察发现，两侧波纹凹槽处管壁的主应力分布规律与Mises 应力分布基本相同。也可以清楚地发现，在两侧波纹凹槽处的管壁有不少区域处于压缩状态，而在中间区域所有管壁均处于拉伸状态。

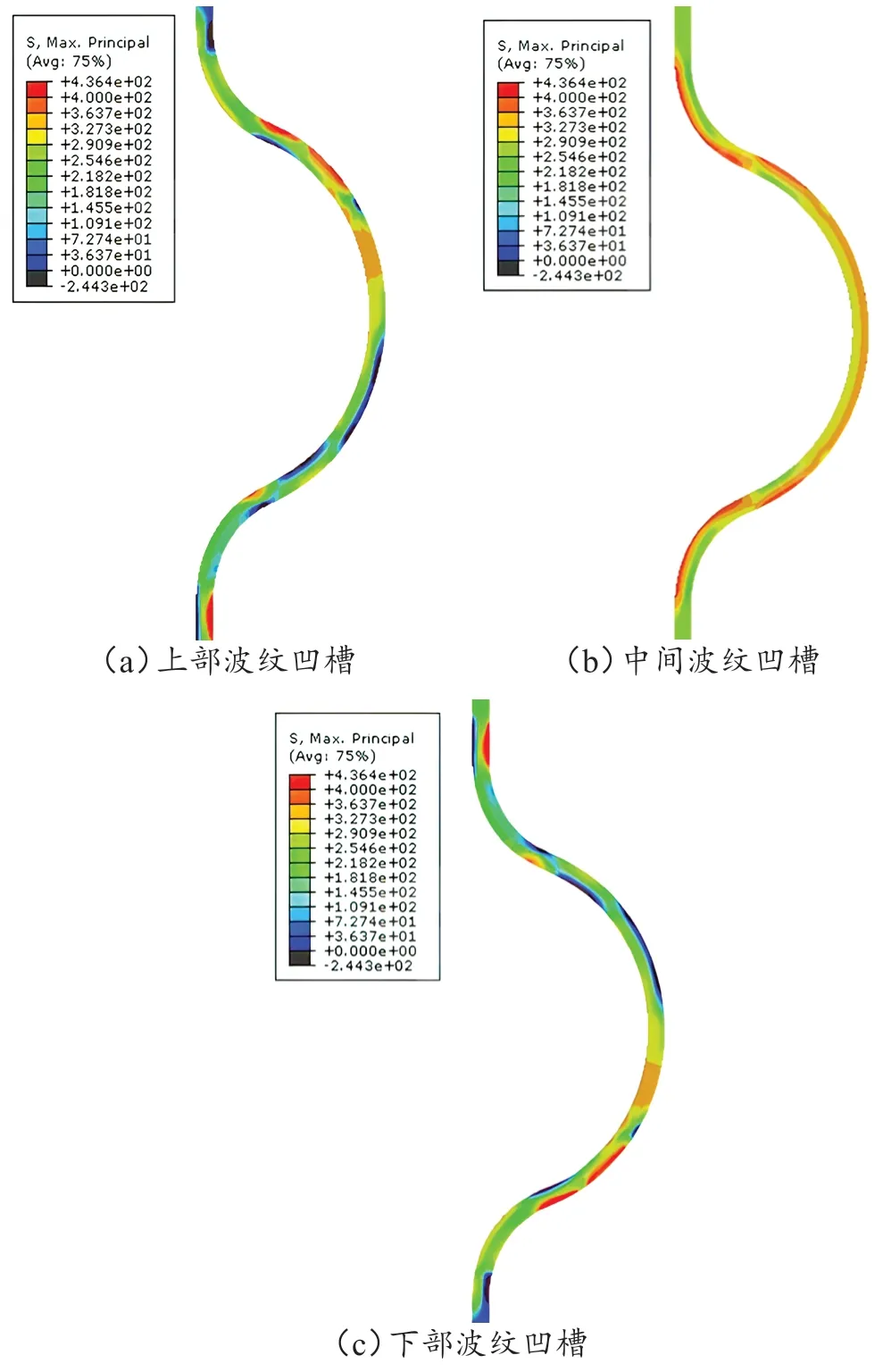
图8 波纹凹槽处的主应力分布云图

2.2 不同摩擦系数的选取对管材成形的影响

分别选取0、0.05、0.1、0.2 四个不同的摩擦系数来考察其对波纹管液压成形工艺和质量的影响。按照上文所述的管壁与波纹凹槽贴合原则，首先判断波纹管贴合时的成形压力。

摩擦系数为0 时，不同成形压力下管壁与波纹凹槽贴合图，如图9 所示。从中可以看出，随着成形压力的不断增大，管壁产生弯曲并逐渐与波纹凹槽贴合。当成形压力在12.55 MPa 附近时，管壁与两端波纹凹槽首先贴合；当成形压力达到20.27 MPa 时，管壁与所有波纹凹槽贴合。所以可知，当摩擦系数为0时管壁的成形压力为20.27 MPa左右。

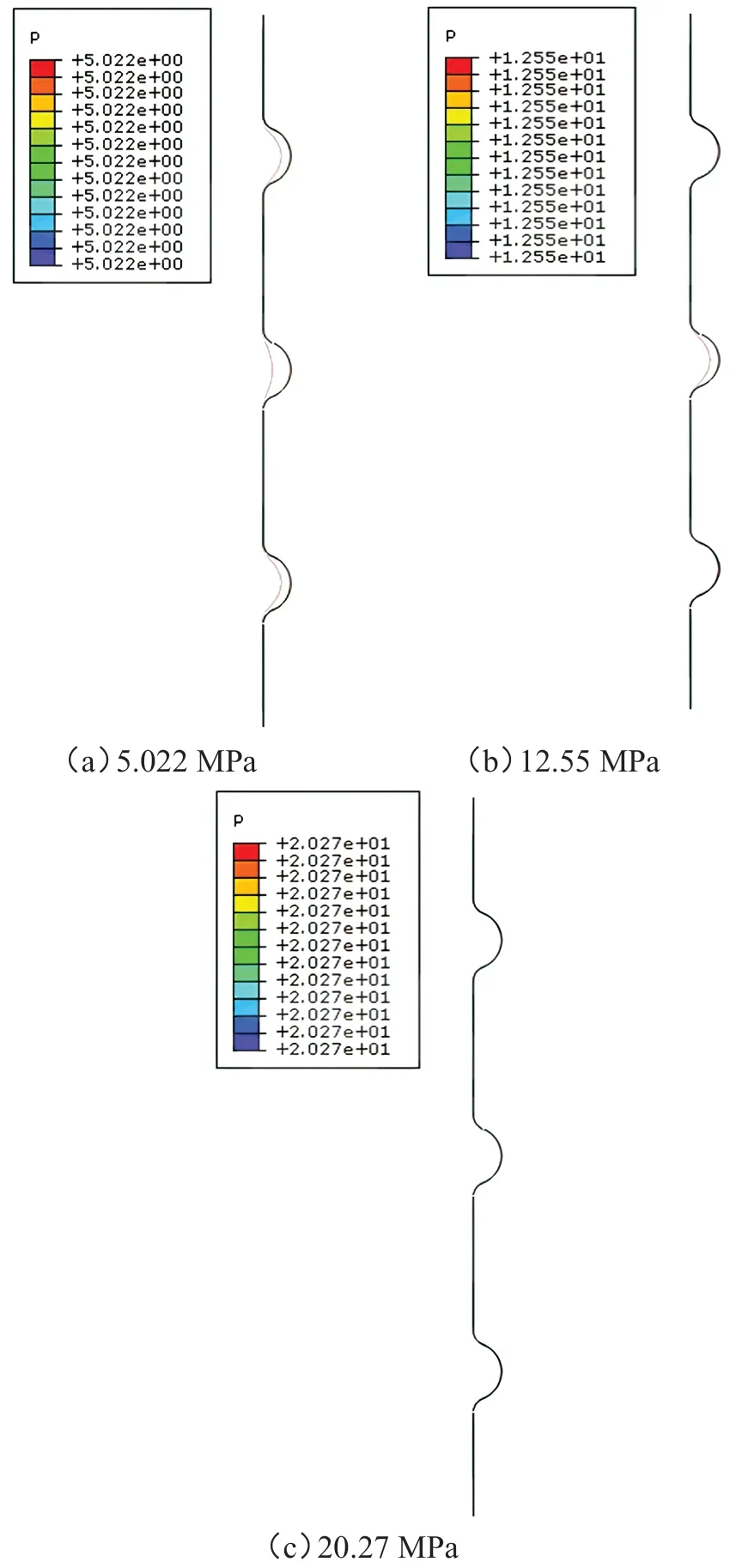
图9 摩擦系数为0时不同成形压力下管壁和波纹凹槽的贴合图

摩擦系数为0.1 时，不同成形压力下管壁与波纹凹槽贴合图，如图10 所示。从中可以看出，随着成形压力的不断增大，管壁与波纹凹槽逐渐贴合。当成形压力为30.05 MPa 左右时，管壁与两侧波纹凹槽完全贴合；当成形压力达到32.94 MPa 时，管壁与中部波纹凹槽完全贴合，但是此时仿真过程已终止。通过观察主应变发现，当成形压力为32.94 MPa 时，中间波纹凹槽处的管壁已经拉伸严重，最大应变达到了1.5，意味着此处出现了破裂，具体如图11所示。

图10 摩擦系数为0.1时不同成形压力下管壁和波纹凹槽的贴合图

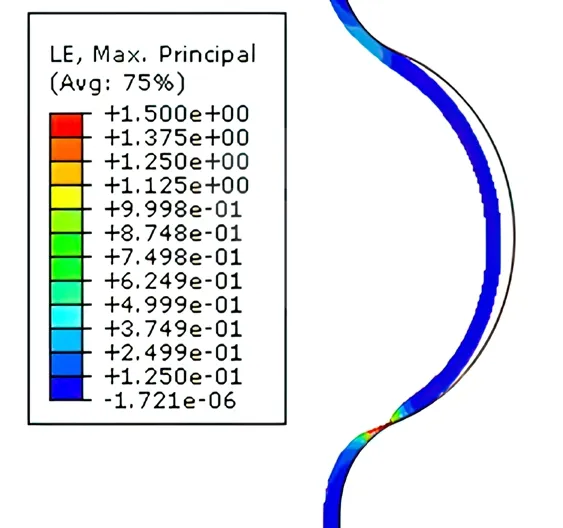
图11 摩擦系数为0.1、成形压力为32.94 MPa 时中间波纹凹槽处的主应变分布

摩擦系数为0.2 时，不同成形压力下管壁与波纹凹槽贴合图，如图12 所示。从中可以看出，随着成形压力的不断增大，管壁与波纹凹槽逐渐贴合，且始终是管壁在两侧波纹凹槽处的弯曲程度大于在中间波纹凹槽处的弯曲程度。但是，本次仿真过程也未能完成。为了分析原因，观察主应变发现，当成形压力为30.82 MPa 时，中间波纹凹槽处的管壁已经拉伸严重，最大应变达到了1.661，意味着此处出现了破裂，具体如图13所示。

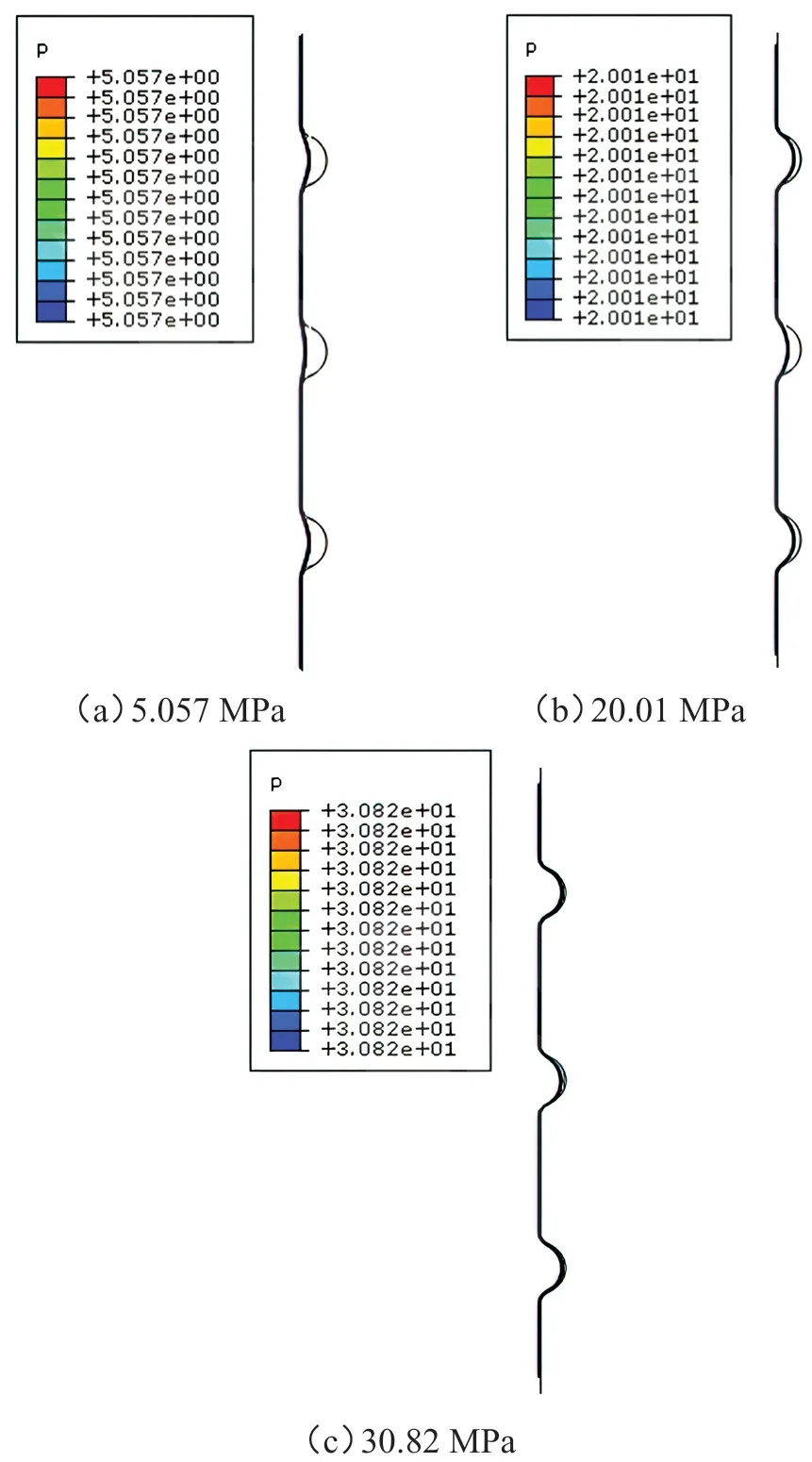
图12 摩擦系数为0.2时不同成形压力下管壁和波纹凹槽的贴合图

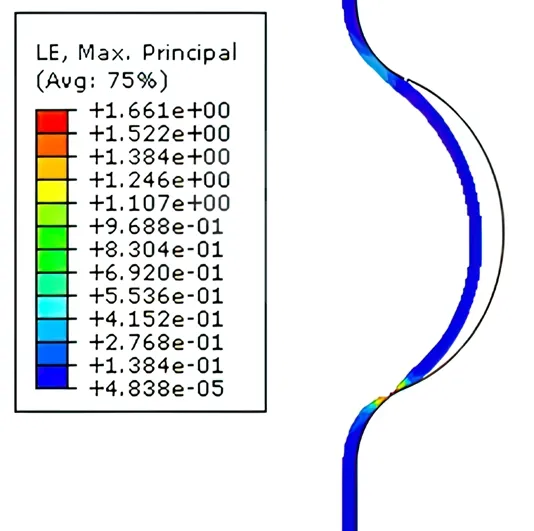
图13 摩擦系数为0.2、成形压力为30.82 MPa 时中间波纹凹槽处的主应变分布

3 结论

本文通过有限元分析的方法对波纹管液压成形工艺进行了数值模拟，并对成形过程中的应力应变场进行了研究。研究结果表明，在波纹管的成形过程中，管壁两端处应力小、中间处应力大，且管材两端处在成形过程中都是压缩状态，中间处则是拉伸状态。此外，摩擦系数对波纹管的成形质量和产品合格率有着重要的影响，需要选择适当的摩擦系数。本研究的结果对于波纹管液压成形工艺的优化和产品质量的提高具有一定的参考价值。