输变电设备典型故障模型及综合维修策略探究

内蒙古电力（集团）有限责任公司 赵继军

1 引言

研究中，相关工作人员基于人工电力系统，尝试构建OPA 典型故障模型。基于输变电设备综合指标以及状态指标，制定综合维修策略。在此基础上，围绕输变电设备定期维修与状态维修两方面内容，对现行的维修措施进行优化[1]。

2 输变电设备典型故障模型

2.1 OPA 模型

OPA 模型的主要目的是研究输变电设备停电时的行为特点。该模型分别采用慢速、快速两个不同的时间量程。前者反映了几天到几年内的变化过程，将该时间段内的负荷变化与性能改善作为锚点，帮助电力系统进行自组织，直至达到动态平衡。后者涵盖了几分钟到几小时内输变电设备停电行为特征变化过程，主要研究输变电设备连锁过负荷和连锁线路故障状态下的停电情况[2]。

OPA 模型基于直流潮流方式，以线性规划方法作为选择标准，计算输电线路功率调度参数。具体计算过程中，研究人员将OPA 模型中的使用价值函数设为C，计算式为：

式中：∑Pi(t)为在单位时间t内，全部输变电设备的总功率；∑Pj(t)为单位时间t内全部负荷节点的总负荷；W为甩负荷过程中付出的代价，取值为100。

OPA 模型作为一种电力系统优化模型，想要确保其能够发挥应有的作用，必须满足下列约束条件：在功率平衡和负荷节点不注入设备功率的情况下，输变电设备的输出功率和线路潮流不能超过极限值。还需要考虑电压稳定性、系统可靠性等约束条件[3]。

2.2 CASCADE 模型

CASCADE 模型的运行逻辑为假设存在n条相同输配电线路，且线路的原始负荷随机分布。设输配电系统初始扰动为d。在该模型框架下，设某一个组件出现故障，则需要根据系统内负荷分配关系来确定故障负荷，并将故障负荷迁移至正常工作组件上。使用该模型的主要目的是对输配电线路故障负荷进行归一化处理，并根据归一化结果计算输配电设备故障组件分布概率函数f。需要注意的是，由于该函数为递归模型，因此利用函数f能够有效体现当n与d不同的情况下，连锁故障导致r个组件出现故障的概率。即满足r＞0，n＞1，0＜d＜1条件的情况下，连锁故障中输配电设备故障组件数量分布概率。

研究中，基于OPA 模型以及CASCADE 模型，尝试构建输配电设备综合维修策略，对现行的设备维修方式进行优化。在保障维修质量的前提下，降低维修成本。

3 制定综合维修策略

3.1 确定权重因素

3.1.1 状态量构成要素

一是原始资料。原始资料是输变电设备交付使用过程中，所涉及的各种信息的记录。常见的原始资料包括铭牌参数、试验报告、出厂验收试验报告、交接报告等。相关工作人员通过阅读原始资料，能够快速了解设备基本信息，确保设备能够安全运行，为设备的维护保养提供必要的支持。

二是运行资料。运行资料是输变电设备在正常运行期间，产生的各种信息的集合。包括运行状况信息、异常状况记录、巡检工作记录等。

3.1.2 状态量权重

根据考虑输变电设备运行稳定性的各个状态量的影响因素，研究人员将其分为四个具体等级，按照从轻到重的顺序排列。对应的权重分别为权重Ⅰ、权重Ⅱ、权重Ⅲ和权重Ⅳ，为方便计算，每项权重的系数用1、2、3、4表示。四个层级中，权重Ⅰ和权重Ⅱ用于描述一般状态量，而权重Ⅲ和权重Ⅳ则用于描述较为重要的状态量。基于输变电设备状态量劣化程度，以2、4、8、10作为对应每个层级的扣分值。

3.2 设备状态与指标之间的关系

状态量的不同，能够体现出不同设备之间的性能差异。如直流电阻工况状态量数据能够反映输变电设备分接开关烧蚀状况，而绝缘电阻、极化指数等数据，则可以反映出输变电线路是否处于潮湿环境之中[4]。此外，还通过气相色谱分析等方法，确定绝缘与导电双重的性能指标。

研究中，为了更好地理解状态量对输变电设备性能的影响，引入隶属度概念。利用隶属度描述状态量对于不同设备和不同指标的重要程度详见表1。

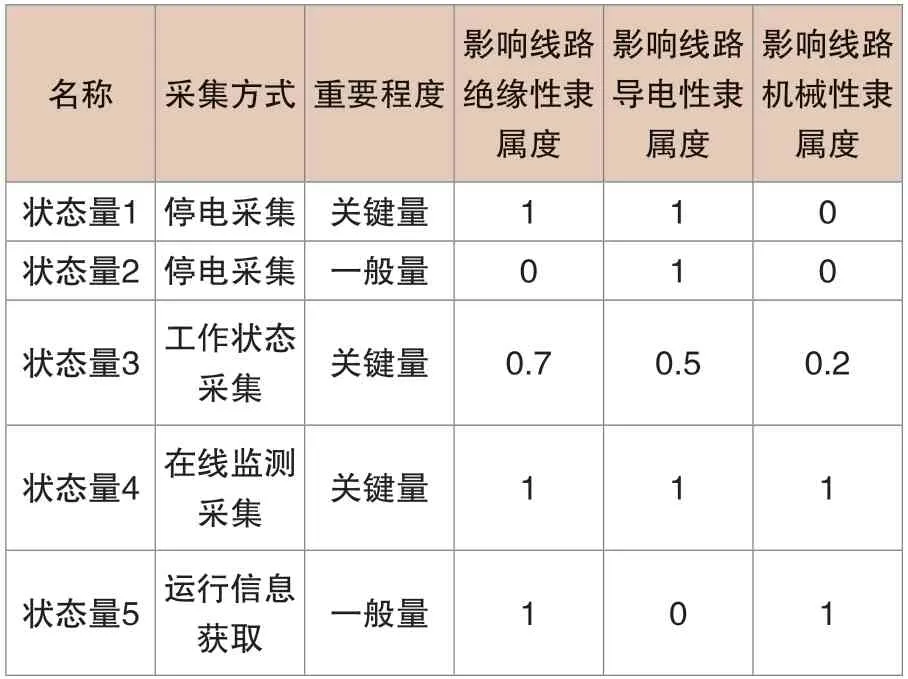
表1 状态量分类表

3.3 状态分析模型

数据来源不同，其状态量评估值也存在很大差异。因此，研究人员需要根据实际检测需求，选择适宜的表达方式，状态量分析模型如图1所示。

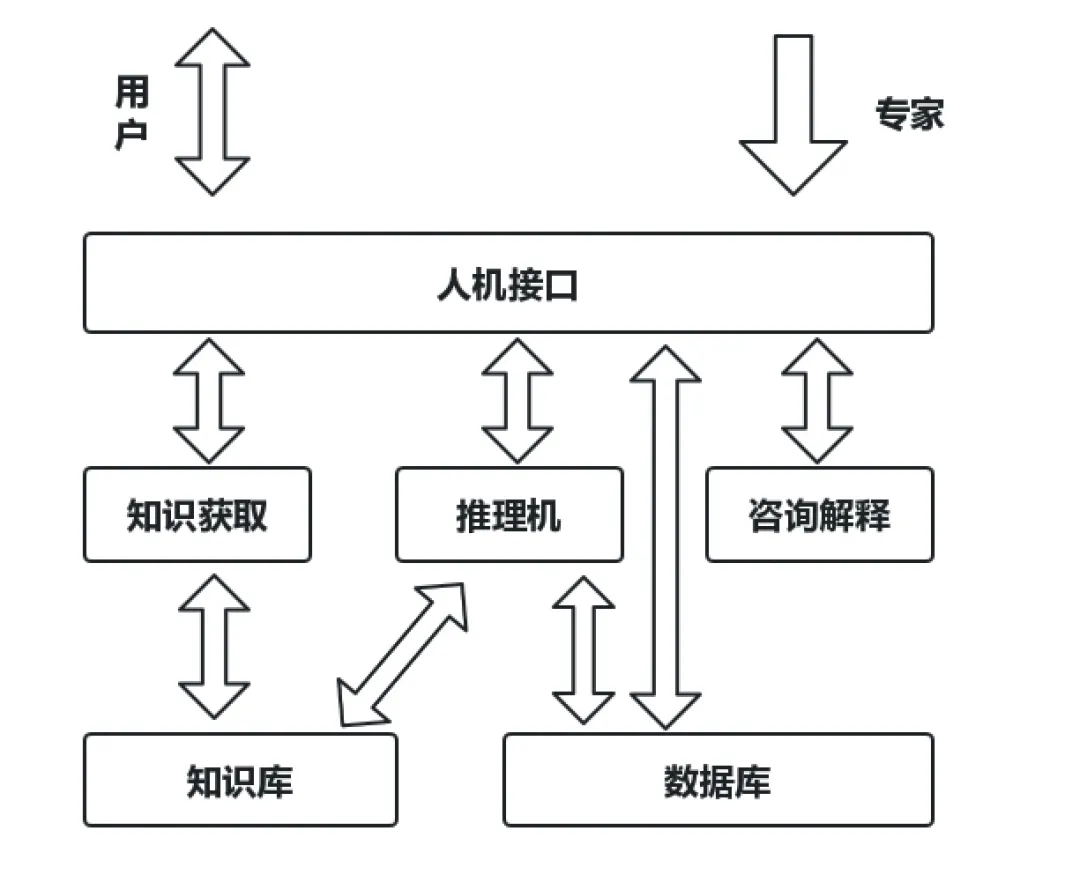
图1 状态量分析模型

基于状态量分析模型，对输配电设备状态量进行综合评估，根据下列式对评估结果进行加权平均处理。

式中：c为输变电设备综合评价结果，该结果需要使用分值的方式进行表示，当c＜15时表示输变电设备综合评价结果为“良好”，若c＞80则表示输变电设备综合评价结果为“不良”；αi为不同状态量结果；∂ij为第i个状态量对于第j个设备性能的隶属度；wi为第i个状态量的重要性，即该状态量的权重。

4 输变电设备维修优化策略

4.1 输变电设备定期维修策略优化

想要对输变电设备定期维修策略进行优化，要遵循的基本原则包括维修成本最小原则和有效度最大化原则[5]。

4.1.1 建立定期维修模型

基于两项基本原则，创建输变电设备定期维修模型。输变电设备定期维修模型如图2所示。

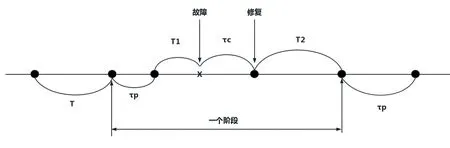
图2 输变电设备定期维修模型

该模型中，T为输变电设备定期维修时间间隔；τp为预防性维修平均用时；τc为故障发生后维修平均用时；T1与T2分别为预防性维修完成时间以及故障修复直至下一个预防阶段所花费的时间，即T=T1+T2。

4.1.2 基于维修费用最低原则的维修策略优化

根据T=T1+T2，研究人员设CT为不同阶段维修费用，Cp代表预防性维修费用，Cc代表事后维修费用。基于维修费用最低原则，将Cp、Ccλ(t)等已知参数代入定期维修模型，计算平均维修费用达到最小值时的参数T。

利用式（3）计算得到的参数T，需要满足以下要求：

4.1.3 基于有效度最大化原则的维修策略优化

在已知λ(t)、τc以及τp具体数值的情况下，研究人员基于定期维修模型，计算参数T，确保其稳态有效度A(∞)为最大值，其计算式为：

根据式（5）计算得到的T值需要满足下列条件：

4.2 设备状态维修策略优化

4.2.1 输变电设备更换及改造时间优化

输变电设备的原始设计质量，会对其寿命造成影响。若设备存在质量缺陷，则其寿命可能会大幅缩短。即使设备进行了维修，其平均寿命也可能会逐渐缩短。针对这一情况，尝试建立输变电设备更换及改造时间优化模型，将输变电设备全寿命过程分成多个周期，并根据实际运行和维修的具体时间进行细分。通过这种方式更加精确地预测设备的故障和维修时间，并制定相应的维护计划，以最大程度地延长设备的使用寿命。

将输变电设备发生第k次故障之前的平均寿命设为λk，则有λk≥λk+1，单位时间内输变电设备维修费用为C，设备零件更换费用为Cf，设输变电设备在发生第N次故障之后更换零件，则C(N)的计算式为：

4.2.2 输变电设备状态检测周期优化

输变电设备检测周期需要参照实际情况进行灵活调整，不宜过长或过短。如果检测周期过长，会导致故障前兆被掩盖，造成设备失效以及其他不必要的损失。而如果检测周期太短，则会造成维修成本浪费问题。因此，研究人员基于最优的检测间隔期τ优化输变电设备状态检测周期，以实现单位时间平均费用最小的目标。这样做可以确保设备的使用寿命得到最大程度的延长，同时也能够有效地控制成本，降低运营成本。在实际应用中，需要对设备进行全面的评估和分析，以确定最适合的检测周期，并持续监测和调整，以确保设备的正常运行和高效使用。

研究人员设输配电设备失效概率密度函数为f(t)，该函数服从指数分布规律，因此可以得到式f(t)=λe-λt，每次检修的间隔时间为τ，若检修人员发现设备失效或者即将失效，即刻对其进行检修。设输变电设备状态检测周期的期望值为TE，则TE与单个检测周期内期望值EC的关系式为：

据此可以得到输变电设备状态检测最佳周期具体数值。

5 结语

输变电设备作为电网系统中的重要组成部分，如何保障输变电设备能够安全、稳定运行成为电力从业人员重点关注的问题。这种背景下，相关研究人员基于输变电设备典型故障模型，以及状态量分析模型，制定具体的输变电设备维修优化策略，为电力系统稳定运行保驾护航。