一类具有牛−羊交叉感染及环境影响的布鲁氏菌病模型

邓金超，张太雷**，康玉娇，刘俊利

(1.长安大学 理学院，陕西 西安 710064；2.西安工程大学 理学院，陕西 西安 710048)

布鲁氏菌病(简称布病)是由布鲁氏菌导致的一种传染性强的人类和动物共患病.它可以一定程度上躲避宿主的免疫反应，也就是说，那些有明显症状的人才会被诊断为患有布鲁氏菌病[1].布鲁氏菌属通过不同的细菌群交替出现，并且可通过垂直传播和分裂传播[2].布病在世界上许多地方都出现地方病，其中包括南美洲、非洲、中亚、中东等地.同时也被世界卫生组织归类为现存主要的“容易被忽视的人畜共患病”之一[3].布病在许多发展中国家是一个公共卫生问题，全球每年确诊的病例数大约有50 万例，但实际患病人数更多[4].

在现实生活中虽然已经有因为输血、骨髓移植而感染的报道，但是人与人之间一般不会进行相互传播.人们感染的主要途径包括食用肉类和未经杀菌的牛奶等直接接触，或者通过在空气中吸入被感染动物所污染的环境颗粒细菌而间接接触感染，并且该细菌可以在动物以外的环境中生存几个月[5].布病症状包括寒战、体重减轻和肌肉以及骨骼疼痛，对于女性而言，还会导致堕胎[6].因为布病会造成动物流产、生育能力降低，并且感染的动物一般不会出现明显的临床症状，所以布病对发展中国家造成了相当大的经济损失，并对人们的健康产生了重大影响[7].内蒙古自治区畜牧业发达，是布鲁氏菌病流行的一个主要区域.2004 年至2018 年，累计报告的布鲁氏菌病例数约为45 408，并且发病率从2004 年的0.046 3/10 万上升至2018 年的0.311 5/10 万，发病率增加了近6 倍.2017 年报告的累计确诊布氏菌病病例为5 485 例，相对于2004 年增加了近810%[8].

从传播动力学的角度有很多学者对布鲁氏菌病进行了研究.例如，Liang 等[9]建立和分析了布鲁氏菌病潜伏期系统，计算出系统的阈值，通过构造函数并应用不变量原理，证明了平衡点的稳定性.Dang[10]等引入环境白噪声对布鲁氏菌病空间传播过程的影响，并考虑一个随机双斑布鲁氏菌病系统，得到了随机系统全局正解的存在唯一性.并且利用随机李雅普诺夫函数理论，得到了一系列随机阈值动力学结果.Hu[1]等提出了一个具有非局部传播和空间扩散的季节布鲁氏菌病流行系统.结果表明，该系统具有全局渐近稳定的无布鲁氏菌稳态的阈值.目前关于具有环境影响的布病传播动力学系统的研究尚不多见，存在大量问题有待解决.

根据上述论述，本文建立了一类具有牛−羊交叉传染以及分别向环境释放布鲁氏菌对人进行直接或间接感染的S IRWSsIsRsScIc模型.

1 模型建立

根据布鲁氏菌病的传播机理，建立系统(1)，将某一区域内t时刻的总人数N(t)分成3 部分：易感者S(t)、感染者I(t)和恢复者R(t).将羊群划分为3 部分：易感羊Ss(t)、感染羊Is(t)和免疫羊Rs(t).将牛群分为两部分：易感牛Sc(t)和感染牛Ic(t).布鲁氏菌会在多个种群之间进行传播，这里主要考虑感染牛、羊和环境交叉感染，以及感染牛−羊对人进行直接感染和感染牛−羊向环境释放布鲁氏菌，然后环境中的布鲁氏菌对人进行间接感染.因此用 W(t)来表示t时刻环境中的布鲁氏菌.传染病系统仓室图如图1 所示.

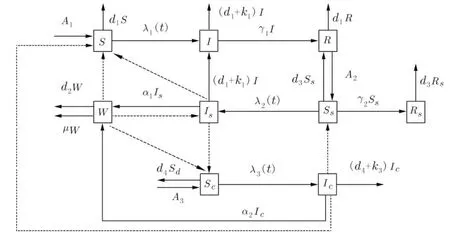
图1 系统(1)的仓室图Fig.1 Flow diagram of model (1)

根据图1，相应的传染病系统如下：

其中：λ1(t)=β1S W+β2S IS+β3S Ic,λ2(t)=β4SsIs+β5SsIc+β6SsW,λ3(t)=β7ScIs+β8ScW，A1，A2，A3分别表示人口的输入率、羊的输入率和牛的输入率，β1，β2，β3，β4，β5，β6，β7，β8分别表示易感人与环境中的布鲁氏菌接触的感染率、易感人与感染羊接触的感染率、易感人与感染牛接触的感染率、易感羊与感染羊接触的感染率、易感羊与感染牛接触的感染率、易感羊与环境接触的感染率、易感牛与感染羊接触的感染率和易感牛与环境接触的感染率，d1，d2，d3，d4，k1，k2，k3分别表示人的自然死亡率、环境中布鲁氏菌的自然死亡率、羊的自然死亡率、牛的自然死亡率、感染人的因病死亡率、感染羊的因病死亡率和感染牛的因病死亡率，α1，α2分别表示感染羊和感染牛向环境中释放布鲁氏菌的比率，γ1，γ2分别表示感染人的治愈率和感染羊的疫苗接种免疫率，µ表示环境中布鲁氏菌的消杀率.

2 无病平衡点的存在性和稳定性

根据Routh-Hurwitz 判据，方程(2)的所有特征根均为负实部.因此，当 ℜ0<1时，无病平衡点P0是局部渐近稳定的.当 ℜ0>1时，P0是不稳定的.证毕.

因为系统(1)前3 个方程是独立于后6 个方程的，因此只需要分析后6 个方程如下子系统:

证明构造Lyapunov 函数

3 地方病平衡点的存在性和一致持久性

4 系统应用

本节将根据系统(1)的特点，以内蒙古布鲁氏菌病为例，展开研究.

4.1 数据布鲁氏菌病的传染性较强，特别是在养殖牛羊的过程中养殖人员的发病率极高，而且传播迅速，目前为止还没有有效的根治方法，严重威胁到了人们的健康.在本节中，我们首先收集内蒙古地区2016 年1 月至2018 年8 月每个月感染布病病例数[8]，然后将数据进行数值模拟与我们的理论结果相结合，这里收集内蒙古地区布病的患病累计病例(图2)进行分析.

图2 2016 年1 月到2018 年8 月内蒙古累计确诊人数Fig.2 Cumulative number of confirmed cases in Inner Mongolia from January 2016 to August 2018

4.2 系统参数估计由内蒙古自治区2015 年12 月人口统计主要数据[14]，可知全区人口约为2 511 万人，出生率为0.007 72，所以取A1=16 154，死亡率为0.005 32，并且因病死亡率为k1=0.而2015 年内蒙古地区牛羊栏数分别为11 259 700 和107 364 900，因为羊的平均寿命为4 到5 a，所以估计羊种群的自然死亡率≈0.222，牛的平均寿命为6 a，所以牛种群的自然死亡率为≈0.167，因此分别取A2=1 986 251，A3=156697.考虑到内蒙古地区牧民很少给环境进行消杀，所以这里环境消杀率取 µ=0.

据公共卫生数据中心得到2016 年1 月感染布病病例数为536，所以这里取感染人数的初始值I(0)=536，然后假设S(0)=2 033 333，根据2015 年12 月的确诊人数以及治愈率得到R(0)=217，由确诊牛羊数以及环境释放率得W(0)=1 114 890，由绵羊数和疫苗接种率得Ss(0)=6 119 799,Is(0)=223 676,Rs(0)=2 827 276，同理得Sc(0)=641 803,Ic(0)=23 458.通过对内蒙古2016 年1 月到2018 年8 月的布病累计数进行数值拟合（图3 黑实线为拟合曲线），得到其他参数.参数的估值见表1.

表1 系统的初始条件和参数值Tab.1 Initial conditions and parameter values of the model

图3 系统拟合Fig.3 Model fitting

由于布病对人们造成严重的损失，所以国家和地区制定相应的政策，用以预防和根除布病.而在此过程中进行疫苗接种具有重要意义，特别是在布病严峻的地区.疫苗的接种会对累计病例数产生较大影响，因此这里仅对内蒙古2018 年9 月至12 月的患病病例数进行预测（图4，黑实线为拟合曲线）.从观察到的数据可以看到，内蒙古地区的患病数依然在增加，人们仍然需要保持时刻警惕的状态，加强预防措施.

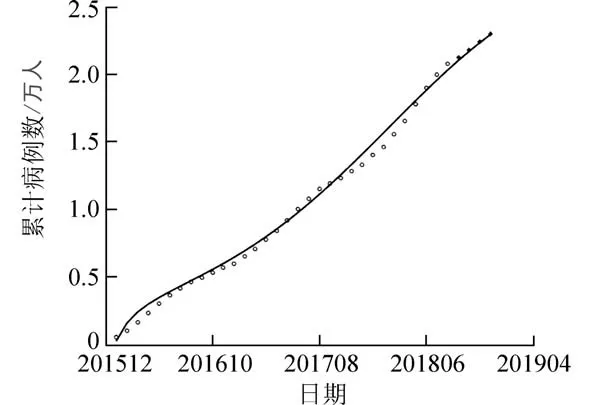
图4 系统预测和真实数据对比Fig.4 Comparison between model fitting and real data

4.3 参数的敏感性分析通过理论分析，布鲁氏菌病能否一直存在的重要参数是基本再生数.为了了解不同参数对它的影响，本文运用敏感性分析确定各个参数对阈值的影响大小，从而得到控制疫情的关键因素.系统（1）的阈值为

由 ℜ0的表达式可以得到，其中有7 个参数 β4,β5,β6,β7,β8,α1,α2对 ℜ0有正影响，有4 个参数µ,γ2,k2,k3对ℜ0有负影响.如图5～图8 所示.不同的参数对疾病有着不同的影响.这里通过理论结合实际，可以得到预防和控制布病的几个措施：（1）控制羊种群内部的相互传染率 β4使其降低；减小单个牛种群和羊群之间的交叉传染传染力 β5和β7，控制环境布鲁氏菌向易感牛−羊的传染率 β6和 β8使其减小；降低感染牛−羊向环境释放布鲁氏菌比率α1和 α2，也就是说对内蒙古地区的感染牛−羊采取相应的检疫工作防止种群内部之间的传染，将牛−羊种群分开喂养防止种群间的交叉感染，尽量降低易感牛−羊在环境中的暴露时长防止环境中的布鲁氏菌对其的感染，对感染牛−羊进行捕杀降低牛羊种群向环境释放布鲁氏菌的比率.

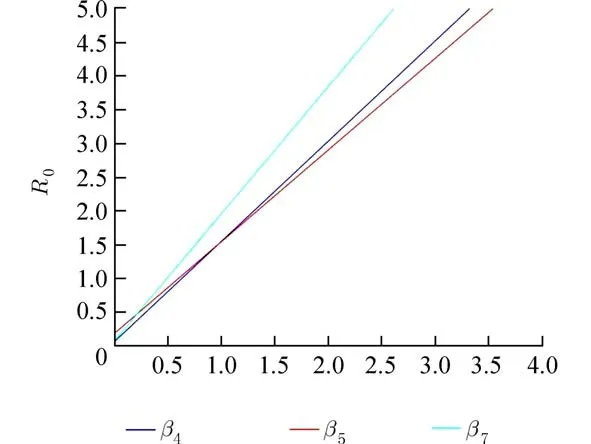
图5 β4，β5，β7 对 ℜ0的影响Fig.5 Effect of β4,β5 and β7 on ℜ0

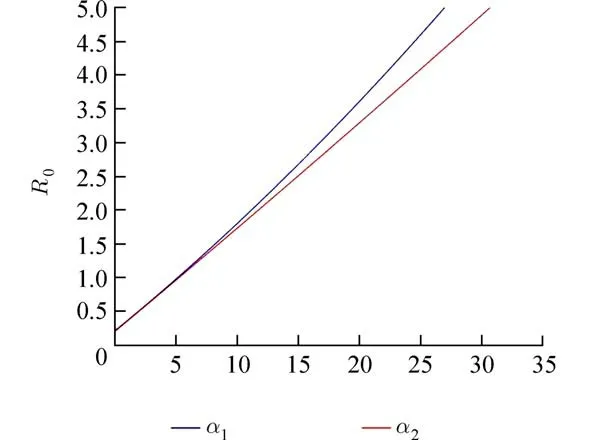
图6 α1，α2 对 ℜ0的影响Fig.6 Effect of α1 and α2 on ℜ0

图7 β6，β8 对 ℜ0的影响Fig.7 Effect of β6 and β8 on ℜ0

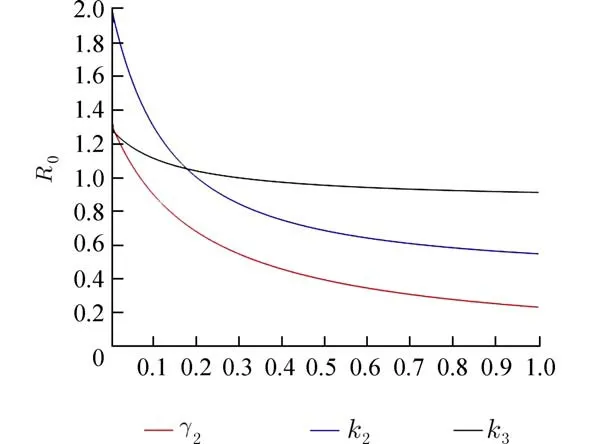
图8 γ2，k2，k3对 ℜ0的影响Fig.8 Effect of γ2,k2 and k3 on ℜ0

（2）增加环境的消杀率 µ和易感染羊的疫苗接种率 γ2，也就是说对环境进行的一定的消杀防止布鲁氏菌对牛−羊的感染，以及全方位的接种疫苗，从根源上降低羊种群对外界的传染率.

由于布鲁氏菌病对任何国家以及各个年龄阶段的人都会进行感染，并且被感染上的人很难治愈，本文分析了环境对易感羊不同的感染率 β6和易感羊不同的疫苗接种率 γ2对患病人数的影响，如图9、图10.

图9 β6的敏感性分析Fig.9 Sensitivity analysis of β6

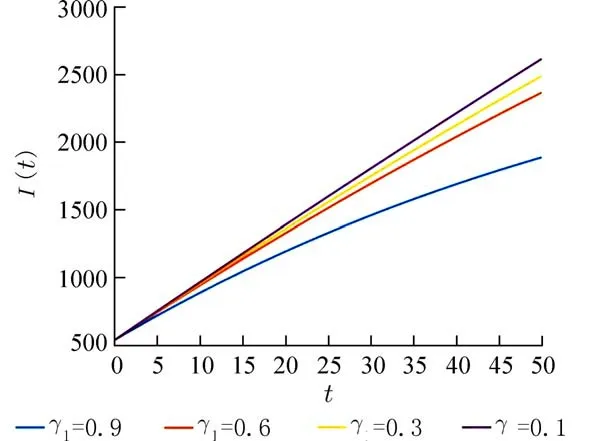
图10 γ2的敏感性分析Fig.10 Sensitivity analysis of γ2

从图9 可以看到，当不断增大环境中布鲁氏菌对易感羊的感染率 β6时，累计病例数也一直在增加，而且随着时间的增加，β6对患病人数的影响是显著的.同样的，不断增加易感羊的疫苗接种率 γ2，累计患病人数会相应减少，并且随时间的增加影响也显著.所以有效控制环境中布鲁氏菌对易感羊的感染以及羊种群的疫苗接种对布鲁氏菌病的预防非常重要，现实中需要将牛羊种群分开喂养以及减少牛羊种群在环境中的暴露时间.并且内蒙古地区应当时刻保持紧张的防控意识，预防和阻止布鲁氏菌病病菌的大面积传播.

4.4 数值模拟利用Matlab 模拟布鲁氏菌模型（1）的解曲线.取初值(S(0),I(0),R(0),W(0),Ss(0),Is(0),Rs(0),Sc(0),Ic(0))=(0.6,0.2,1,0.1,1.1,0.11,0.5,1.4,0.2).

（1）取参数A1=0.1,A2=0.2,A3=0.14,β1=0.0 012,β2=0.0 013,β3=0.003,β4=0.0 011,β5=0.0 015,β6=0.001,β7=0.0012,β8=0.0011,d1=0.02,d2=0.01,d3=0.03,d4=0.04,k1=0.045,k2=0.091,k3=0.086,α1=0.09,α2=0.08,γ1=0.05,γ2=0.01,µ=0.015，此时满足定理2 的条件 ℜ0<1，得到图11.此时可以看到布鲁氏菌模型的无病平衡点的全局稳定.

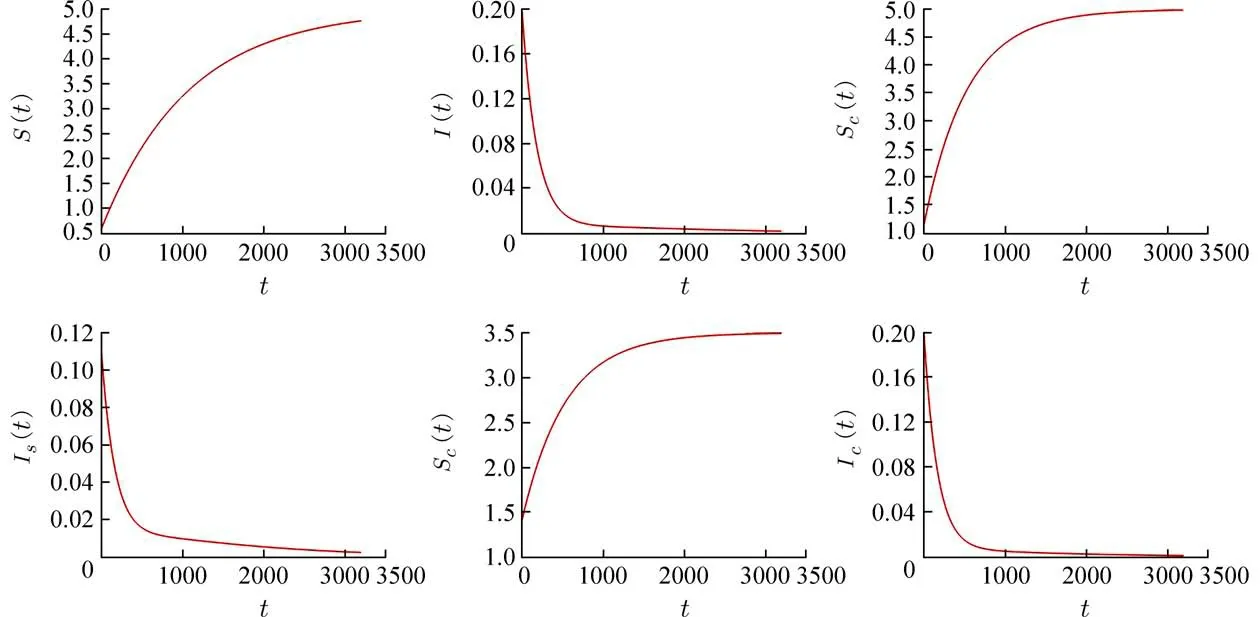
图11 ℜ0<1时，模型(1)解的拟合Fig.11 The fitting of the solution of model (1) when ℜ0<1

（2）改变条件中（1）的β1=0.12,β2=0.23,β3=0.13,β4=0.061,β5=0.085,β6=0.26,β7=0.092,β8=0.071,k1=0.045,k2=0.041,k3=0.066,α1=0.15,α2=0.25,γ1=0.15,γ2=0.25，其余参数不变，此时满足定理4 的条件 ℜ0>1，得到图12.此时可以看到布鲁氏菌模型的地方病平衡点的一致持久性.

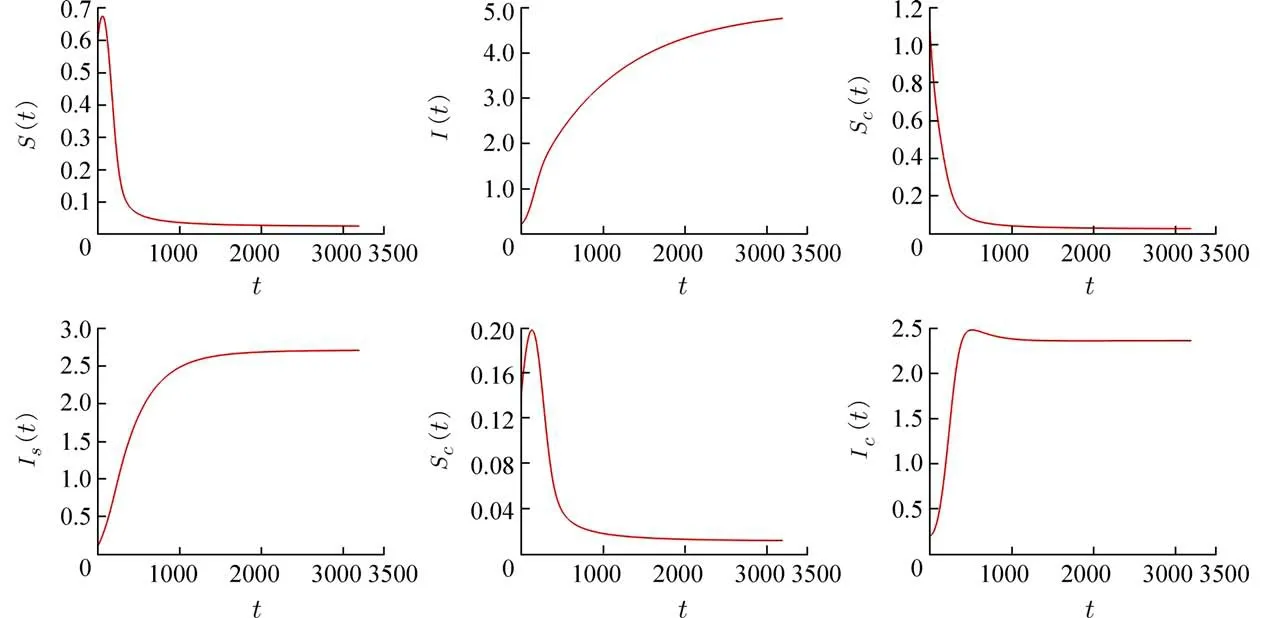
图12 ℜ0>1时，模型(1)解的拟合Fig.12 The fitting of the solution of model (1) when ℜ0>1

5 总结

本文建立了公共环境牛−羊种群交叉传染对人直接和环境对患病人数间接影响的SIRWSsIsRsScIc系统，求解出系统的阈值−基本再生数，证明了无病平衡点的全局稳定性以及疾病是一致持久的.将系统与内蒙古地区2016 年1 月至2018 年8 月布鲁氏菌病累计患病人数拟合，并且用系统预测的2018 年9 月至12月患病人数与真实数据对比，同时计算出内蒙古布鲁氏菌病的阈值 ℜ0大约为1.404 7，以此说明布鲁氏菌病将在内蒙古地区成为地方病.根据敏感性和不确定分析得到，对内蒙古地区的感染牛−羊采取相应的检疫工作、将牛−羊种群分开喂养、减少易感牛−羊在环境中的暴露时间以及对感染牛−羊进行捕杀、对环境进行的一定的消杀，可从根源上降低羊群对外界的传染率.因此内蒙古地区布鲁氏菌病控制的关键是结合隔离喂养、检疫工作、环境灭菌、疫苗接种以及扑杀等多项措施，且提高人们的防控意识也很重要.