基于改进麻雀算法的铜带排样优化应用

顾雨娟，李学兵

（湖北汽车工业学院电气与信息工程学院，湖北十堰 442000）

具有多品种小批量市场供货特点的铜加工企业的铜带产量和铜带消费量巨大，成材率的提高对此类企业降低生产成本、提高竞争实力十分重要。目前在铜合金的成分设计和制备加工工艺等方面已经取得了一定的研究成果，铜带的质量得到保证，所以影响成材率的关键工序在于剪切工序，选取的排样方案直接决定产出成品的多少[1]。铜加工企业大多生产以订单为导向的定制产品，一卷母带原料会根据不同的订单需求剪切出十几种子卷，不合理的排样方案会直接导致后续包装工序工作量增加，难以及时交付成品。因此，寻找一个高效的排样方案对剪切工序来说至关重要，剪切工序排产优化实际成为在最优排样方案下的排产问题。

优化剪切工序的排样模型方案属于一种具有较高计算复杂度的NP-hard带有工艺约束的矩形件排样优化问题，目前的研究虽然都以提高成材率为目标，但未能同时解决涉及剪切工序的“一刀切”约束和长度浮动约束的问题[2-5]。采用匀质块的思想和罚函数处理这两种约束，最后采用Singer混沌序列提高初始种群多样性结合柯西变异提升后期寻优精度，自动生成排样方案，在保证交付期限的情况下提高了成材率。

1 问题描述与数学模型

1.1 问题描述

剪切工序可以分为两个阶段：第1阶段使用圆盘剪，根据排样方式对母带铜卷进行排刀横向剪切；第2 阶段使用切头剪，纵向剪切母带后分切出若干子卷。其中，第2 阶段纵剪母带至完全切断即为“一刀切”工艺约束，剪切排样示例图如图1。将n种宽度、长度无限长的卷材，剪切出m种长度为li、宽度为wi、需求量为bi的矩形毛胚，母带卷料剪切得来的子卷宽度固定，长度在一定范围内浮动，要求在约束条件内，寻找一个剪切优化排样模型方案使消耗的卷材面积最小。

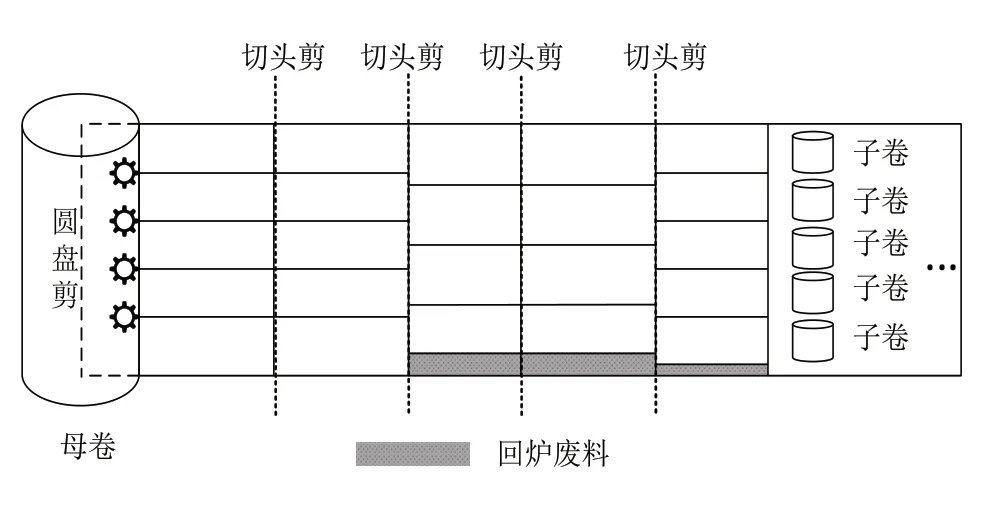
图1 剪切排样示例图

1.2 数学模型

一个排样模型方案由多种排样方式组合而成，且每种排样方式均有相应的使用次数，通过限制每种排样方式的最大使用次数来处理对各个成品需求量的约束，同时防止因过量生产占用过多仓库库存。

设共有m种待剪矩形毛胚，n种可供排样选择的卷材，e种待考察的排样方式，建立数学模型：

式（1）表示目标函数是使所消耗的卷材面积最小；式（2）第一条表示剪切卷材得来的毛胚数量需满足订单需求的数量，第二条表示每种排样方式的最大使用次数约束。

符号定义：Z为下料方案中消耗卷材的总面积；C=[c1,c2,…,ce]T，cj为按照第j种排样方式剪切矩形毛胚使用卷材的面积，1 ≤j≤e；X=为按照第j种排样方式剪切矩形毛胚的使用次数，1 ≤j≤e；Q=[q1,q2,…,qe]T，qj为按照第j种排样方式剪切矩形毛胚的使用次数上限，1 ≤j≤e；B=[b1,b2,…,be]T，当1 ≤i≤m时，bi表示第i种毛坯的需求数量，当(m+1)≤i≤(m+n)时，考虑到不限制每种可供排样卷材的使用次数，令bi=0，故=0；A：m行e列矩阵，当1 ≤i≤m时，aij为按照第j种排样方式剪切卷料时得到第i种毛坯的数量；当(m+1)≤i≤(m+n)时，aij为按照第j种排样方式剪切矩形毛胚使用第（i-m）种卷材，考虑到一种排样方式只能使用一种卷材

2 剪切排样方案设计

2.1 获取排样方式

采用普通两阶段排样方式（图2）虽然也可以满足“一刀切”的工艺约束，但后续仍需要进一步剪切加工为成品矩形毛胚，无疑会给企业增加更多的切割成本同时延长交付时间。

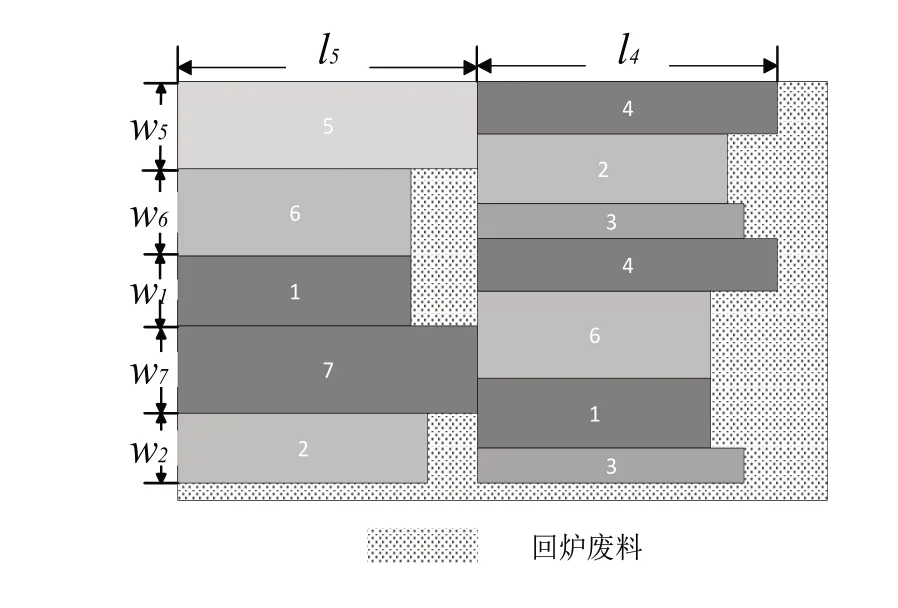
图2 普通两阶段排样方式

实际剪切生产环境中，子卷被剪切后需要立即完成包装操作，不同规格的成品由不同的箱子进行装箱，这种排样方式也会增加包装工序的复杂性。求解模型算法需要调用本节算法获取排样方式，每种排样方式选取的待排毛胚种类过多会影响算法的整体性能。采用普通两阶段排样方式“一刀切”下来会产生较多的废料，不利于提高成材率。

为了简化实际生产中的切割工艺并减少剪切卷材后续的包装工序的操作复杂度，同时提升求解算法性能且尽量减少废料面积，采用匀质块的思想进行矩形毛胚的排样布局（图3），各个匀质块中仅含同有一种规格的矩形毛胚，由切头剪竖直“一刀切”下来的待剪毛胚最多两种最少一种，当前用来排样的卷材的剩余的不可使用宽度小于当前待排毛胚的最小宽度，并规定卷材的宽度利用率达到90%以上。

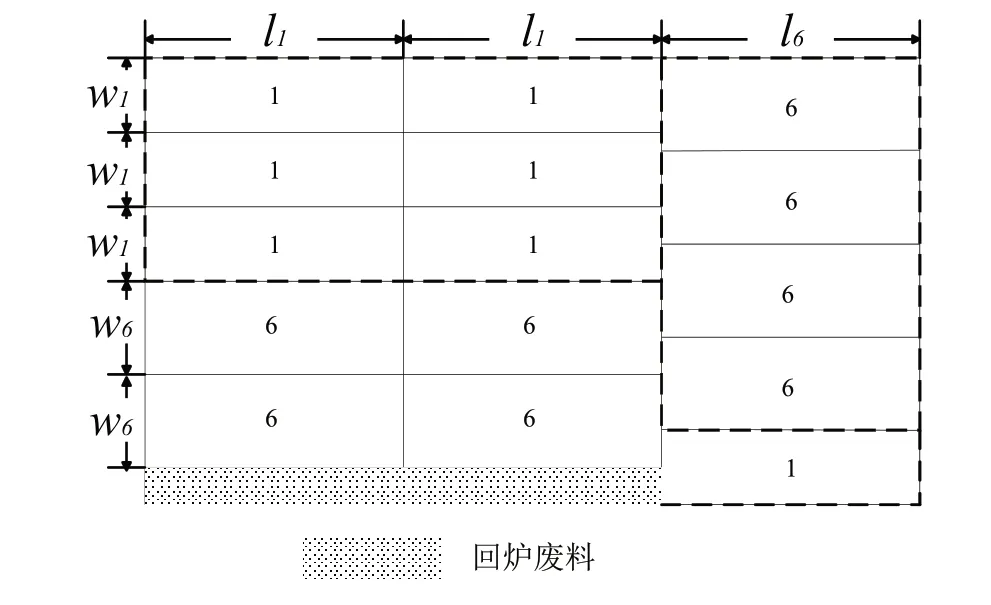
图3 匀质块两阶段排样方式

设：可供排样的卷材宽度有n种宽度，N={W1,W2,…Wn} ；待排毛坯宽度有m种宽度，M={w1,w2,…wm} ；当前待排毛胚的最小宽度为w'(w'∈M)；当前使用排样的卷材宽度为W'(W'∈N)。当排样方式仅含有一种毛胚，设第j种排样方式由第1 种毛坯剪切，则第j种排样方式使用次数上限由式（3）求出，其中ceil()函数为向上取整函数。

式（4）表示设第j种排样方式只剪第1 种毛胚时的数量约束。

当排样方式含有两种毛胚，设第j种排样方式由第1、2 种毛坯剪切，则第j种排样方式使用次数上限由式（5）求出。

式（6）表示设第j种排样方式剪第1、2 种毛胚各自的数量约束。

在实际生产环节中，包装工序同时进行单卷卷称重，工人根据子卷的卷重是否在订单要求的最低卷重和最高卷重范围之间判断是否可以发货，所以在拿到订单时需要对相关数据进行预处理，根据母带卷料的铜合金密度、卷料厚度，计算出每种规格的成品交付时的最大长度和最小长度，即实际长度在最小长度和最大长度范围内即可。为了求取各个排样方式的有效长度，首先求出各个排样方式的下限长度U={u1,u2,…ue}，上限长度V={v1,v2,…ve}，对二者取交集得出每种排样方式的长度范围。

3 求解算法

首先根据2.1 节排样算法获取每种排样方式的待剪毛胚种数、待剪毛胚数量以及排样方式长度范围，然后以改进麻雀搜索算法作为求解算法。

3.1 问题编码与解码

将每种排样方式使用对应卷材的总面积(每种排样方式使用卷材的面积C×每种排样方式的使用次数X)作为决策变量，其中一个解可以表示为P={p1,p2,…pe}，pj表示第j种排样方式剪切卷材的总面积，则pj需要同时满足式（7）和式（8），其中1 ≤j≤e,1 ≤t≤n,k∈N+，Wt为第j种排样方式使用的卷材宽度。

式（7）为P的可行解范围，式（8）为矩形毛胚的长度浮动约束，以及限制排样方式的使用次数必须为整数。

3.2 适应度函数设计

f为适应度函数值，f越小，下料方案使用卷材的总面积越少，卷料利用率越高，适应度越好。对于不满足式（7）和式（8）约束的解，将会生成一个罚函数，将第j种排样方式生成的罚函数值设为为yj，令yj≫pj，罚函数加到原适应度函数值上，通过比较原适应度函数的值，不符合约束的将会成为劣解并被淘汰。

3.3 改进麻雀搜索算法

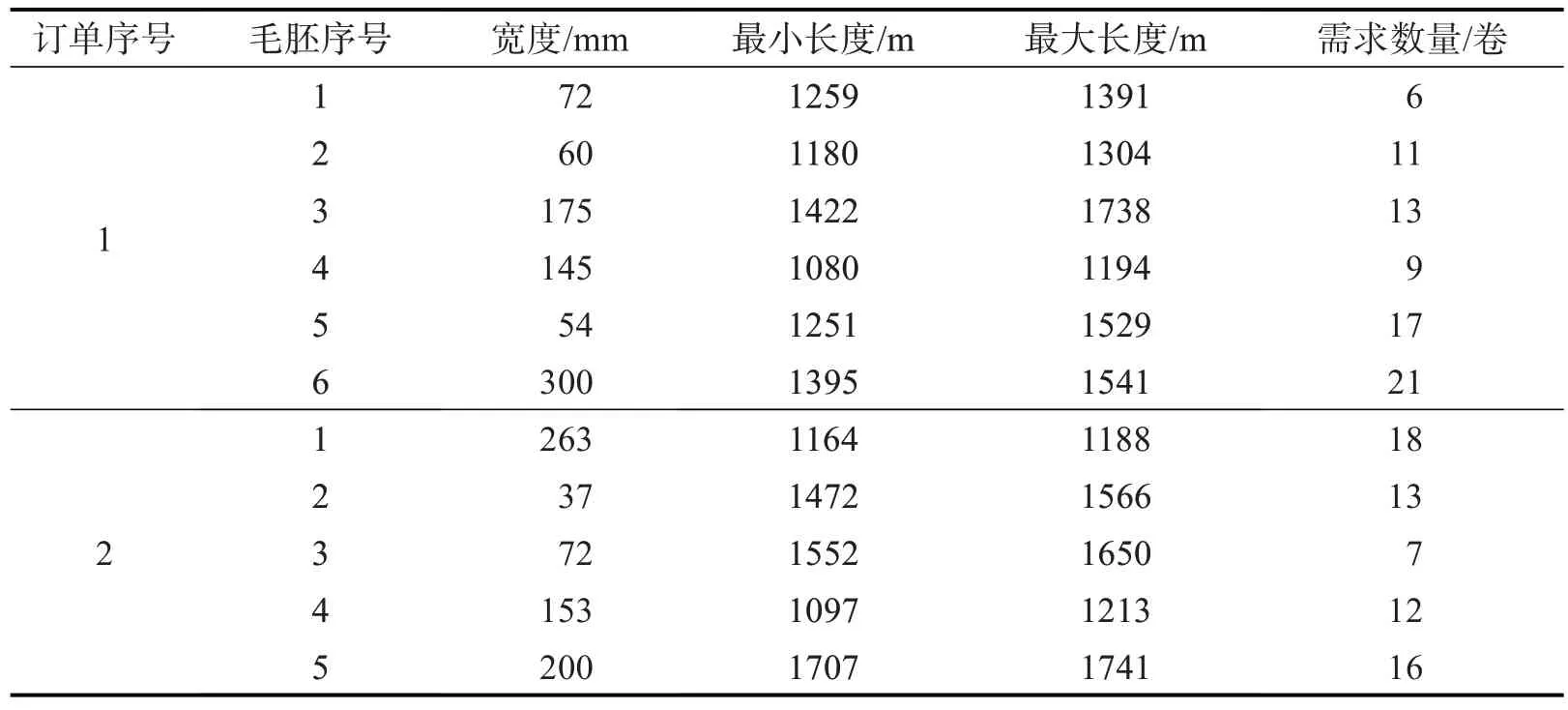
标准麻雀搜索算法(SSA)是受麻雀群体觅食行为启发而来[6]，模拟其在自然环境中寻找食物和避开天敌的行为以寻找最优解，可简单抽象为寻找者－跟随者模型。寻找者在种群中引领搜寻食物的方向，跟随者时刻监视寻找者的方向并跟随移动，二者身份动态变化，在麻雀群体中随机选取10%～ 20%为预警者，一旦发现有天敌靠近，则向安全区域移动。SSA算法原理为：

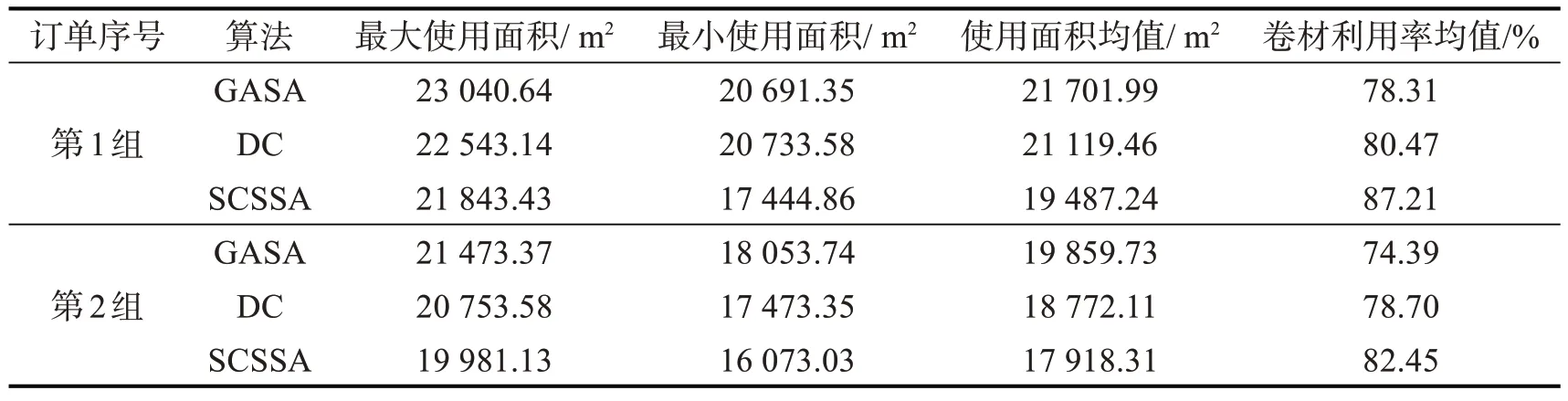
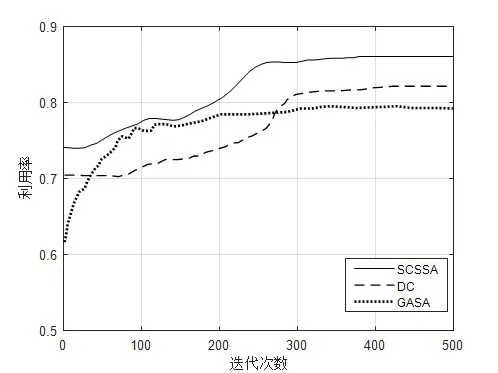
式（10）为发现者位置更新方式。t和T分别为当前迭代次数和最大迭代次数，α为0 到1 之间的随机数，Q为服从正态分布的随机数，R和ST分别为捕食过程中的预警值和安全值，R∈[0,1]和ST∈[0.5,1]。当R

3.3.1 Singer混沌

Singer映射是一种典型的混沌映射，相比于其他混沌映射，其数学表达式简单，参数较少，可使初始解更加均匀地分布，在一定程度上提升种群多样性，并且在迭代初期加快搜索速度，其表示形式为：

3.3.2 柯西变异机制

麻雀群体在寻找食物的过程中，跟随者往往在具有较高适应度值的发现者附近食，进而转换身份成为发现者，这就会导致算法陷入局部最优，降低算法寻找最优解的精度。为了避免这种情况，在标准麻雀搜索算法中引入柯西变异机制跳出局部最优解，跟随者位置更新变异公式为：

3.4 算法步骤

步骤1：初始化各个生产参数、麻雀算法参数，调用2.1 节算法获取排样方式组合A，单卷使用卷材长度下限U、上限V，排样方式使用次数上限Q。

步骤2：用公式（13）对麻雀种群进行初始化，使之生成均匀分布的混沌序列。

步骤3：计算每个麻雀位置对应的适应度函数值，并记录全局最优解和全局最差解。

步骤4：对麻雀种群依据适应度函数值进行排序，选取排序值前30%的麻雀为发现者，其余为跟随者，用式（10）和式（11）更新发现者和跟随者位置。

步骤5：在麻雀种群中随机选取15%个体为预警者，用式（12）对预警者进行位置更新，并更新全局最优解和全局最差解。

步骤6：对跟随者按一定概率用式（14）进行柯西变异，若变异后适应度更高则替代原来位置，否则不变。

步骤7：达到最大迭代次数，结束算法，否则继续迭代步骤3。

4 实验结果与分析

为了检验求解算法的合理性，测试了来源于湖北精益高精铜板带有限公司的实际生产数据，通过对客户订单数据进行预处理后得到单卷最小长度、最大长度、成品宽度和需求量见表1，可供排样的卷材为厚度0.1 mm，宽度分别为420 mm 和350 mm，铜含量99.95%以上，含氧量0.01‰以下，导电量大于98%IACS的TP2紫铜带。

表1 生产实例中的订单需求数据

仿真实验运行在MatlabR2022a 上，设定种群大小为20，最大迭代次数500，分别独立运行5 次，将遗传模拟退火算法(GASA)、基于排挤的小生境遗传算法(DC)[8]、改进麻雀搜索算法(SCSSA)三种算法在相同环境中进行对比运算，结果见表2。

表2 排样求解结果

为了分析对比结果，卷料利用率迭代收敛曲线图如图4。经过Singer 混沌结合柯西变异的改进麻雀算法SCSSA 算法在卷材利用率、寻找最优解能力等方面明显高于另外两者算法，这是因为GASA 算法在寻找最优解后期有易陷入局部最优解的缺陷，DC 算法在处理相似解的判断和替换能力上表现欠佳，而SCSSA 引入的柯西变异机制能够限制陷入局部最优解，提高寻优能力。

图4 迭代曲线收敛图

5 结语

针对基于剪切优化排样模型方案的滚动排产问题，以消耗最少母带卷料面积为目标建立了排样优化模型，依据排样结果来进行滚动排产。从排样方式上讲，基于一种匀质块的思想设计矩形毛胚的排入顺序，不仅有利于指导工人在实际生产中简化卷材剪切工艺，也减少了后续成品包装工序的操作复杂度，加快了交付进程；从求解算法上讲，使用改进的麻雀搜索算法进行求解，相比其他算法在卷料利用率方面有更优秀的表现，全局寻优和局部寻优能力更强。由于实际剪切工序在分剪时不可避免地出现带头带尾损耗，在今后的研究中将进一步通过数据分析，并在客户接受的一定程度内考虑成品卷重、数量超发减发的情况，建立相应的优化模型使成材率更加精确。