二次函数的实际应用

胡友明

利用二次函数解决相应的实际问题，是中考的常考题型。虽然有难度，但是如果我们能抓住关键因素，便能轻松化解。下面以2022年浙江省台州市的一道中考题为例加以说明。

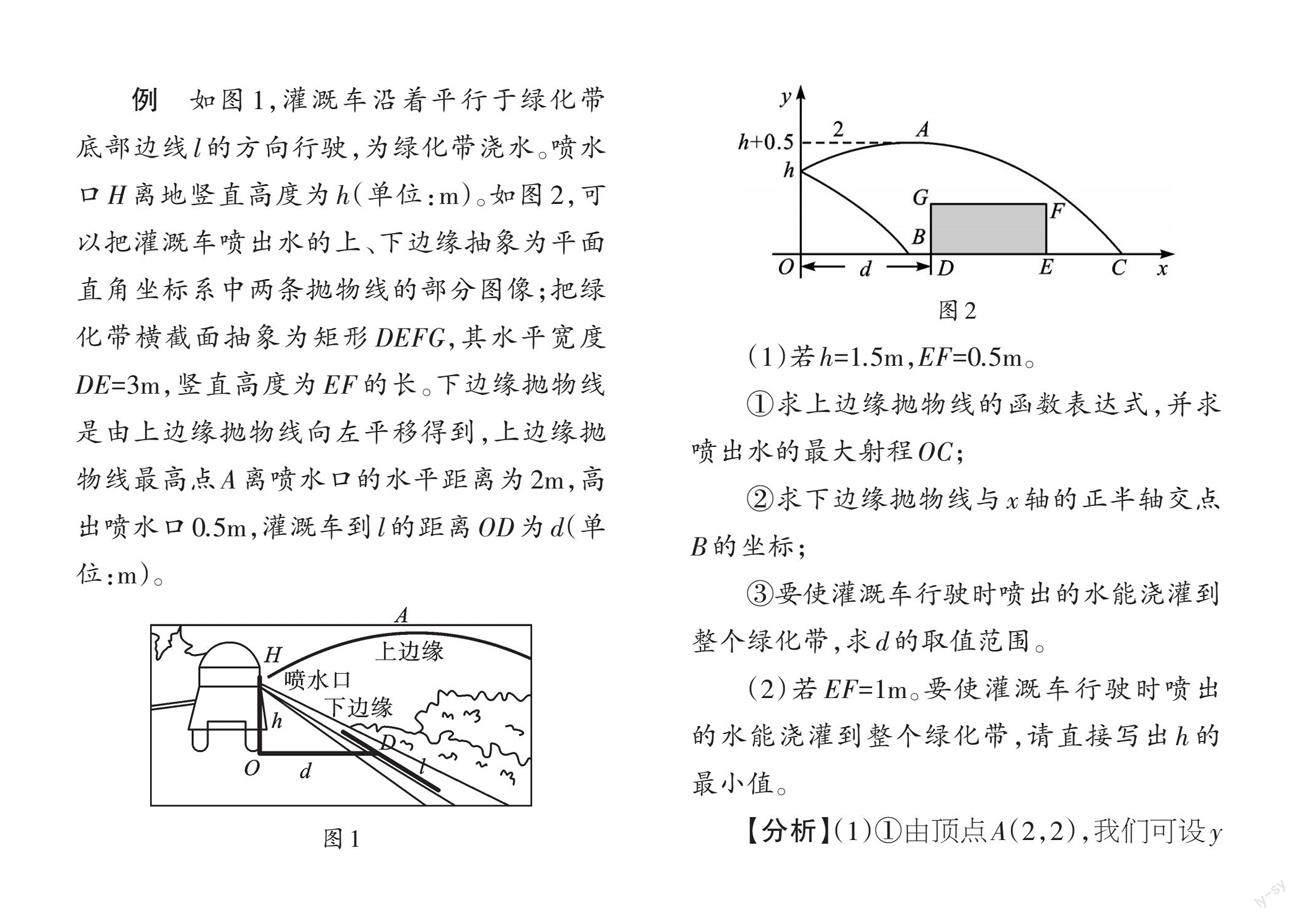
例 如图1，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水。喷水口H离地竖直高度为h（单位：m）。如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图像；把绿化带横截面抽象为矩形DEFG，其水平宽度DE=3m，竖直高度为EF的长。下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到l的距离OD为d（单位：m）。

（1）若h=1.5m，EF=0.5m。

①求上边缘抛物线的函数表达式，并求喷出水的最大射程OC；

②求下边缘抛物线与x轴的正半轴交点B的坐标；

③要使灌溉车行驶时喷出的水能浇灌到整个绿化带，求d的取值范围。

（2）若EF=1m。要使灌溉车行驶时喷出的水能浇灌到整个绿化带，请直接写出h的最小值。

【分析】（1）①由顶点A（2，2），我们可设y=a（x-2）2+2，再根据抛物线过点（0，1.5），可得a的值，从而解决问题；②由对称轴知点（0，1.5）的對称点为（4，1.5），则下边缘抛物线是由上边缘抛物线向左平移4m得到的，可得点B的坐标；③根据EF=0.5，求出点F的坐标，利用抛物线的增减性可得d的最大值和最小值，从而得出答案。

（2）当喷水口高度最低，且恰好能浇灌到整个绿化带时，点D、F恰好分别在两条抛物线上，故可根据两条抛物线表达式设出点D和点F的坐标，再由图分析出纵坐标差为EF，从而得出答案。