计算机智能优化技术在大型复杂钢结构项目中的应用

李 逊, 邓林忠, 李俊超, 欧启捷, 劳恒辉, 王 森

(广东众图科技有限公司，佛山 528200)

0 引言

优化起源于1869年的麦克斯韦尔理论,属于一门交叉学科,目前已在微电子、航空航天、机械制造及土木工程中得到广泛应用[1-2]。传统上建立结构优化方程及约束条件需考虑实际工程的设计要求。而实际工程特别是大型工程具有复杂的约束条件和复杂的实际应用环境,导致结构优化方程的建立和求解极端困难,从而限制了优化在土木工程中特别是超大型结构工程中的应用。在应用优化技术分析大规模项目时,存在项目构件数量多、约束条件多及构件之间相互约束等困难。假定项目的构件数量为10 000个,每个构件可选截面为10个,搜索空间达到1010 000,在如此大的数量中计算最优结果是极为复杂的。实际项目的约束需要满足受力、构造及建筑条件的要求,单构件的改变引起相关构件的受力改变,更增加优化收敛的复杂性。优化需发展新的算法以满足工程需求[3-8]。

人工智能技术与结构优化的结合是重要的发展方向[9]。由于工程实际项目的复杂性及计算能力的限制,目前大部分的结构智能优化研究往往应用在单构件、简单算例、中小型项目及有固定特性的工程上。本文通过简化约束条件,发明了针对工程优化的智能求解技术,成功实现了人工智能技术在优化大规模钢结构项目领域的应用。

1 传统优化方程和约束条件

以钢结构中心支撑项目为例,传统优化方程和约束条件建立如下[10]:

(1.1)

s.t.δi≤f

(1.2)

δi≤φbf

(1.3)

νi≤[νT]

(1.4)

⋮

(1.n)

式(1.1)为目标函数,其中Li、Ai分别为第i根构件的长度和横截面积;ρ为钢材料密度;WL为项目构件总重量;N为构件总数量。式(1.2)～(1.n)为计算机优化所需的约束条件。其中式(1.2)为强度条件,δi为i构件相应的应力,f为相应的设计强度;式(1.3)为受弯构件整体稳定条件,φb为整体稳定系数,不同类型的构件应相对调整;式(1.4)为挠度条件,νi为第i根构件的挠度值,[νT] 为挠度限值;式(1.n)为规范构造的约束条件,bi为第i个构件翼缘板的外伸宽度,tif为第i个构件翼缘板厚度,[υf]为规范翼缘宽厚比限值。强度、稳定、构造针对不同的构件类型、截面形式又需要做不同的调整。另外实际项目需满足建筑功能、构造等约束要求,大规模项目约束条件的建立是一项费时费力的工作。

2 新型结构优化模型方程

假设所有杆件截面参数为X={Xi,i=1,2,3,…,k} ,k为所有的优化变量总数,更具体的说X包括所有的梁柱截面的翼缘宽度b、厚度t及高度h等几何参数。笔者建立的新型优化方程如下:

目标函数为:

(2)

式中:f(x)为造价目标函数;ψ为钢结构造价系数;Xi、Xi low、Xi upp为分别为构件截面大小及其对应的上限值和下限值;F为在结构计算分析过程中不符合规范条文要求的点数量。

应用结构计算分析软件对X参数进行设计分析,当不符合规范要求时,设计分析软件会产生警告信息。考虑所有的约束条件,当F>0时,表示结构有些约束条件没有满足,其具体没有满足的约束条件可以通过结构分析的结果比如PKPM或YJK的结果得到。当警告信息为F=0时,即结构满足强度、稳定及构造等约束。

方程(2)与传统优化方程(1)比较,具有以下创新:实现了优化计算和结构分析的分离,使得优化计算与结构分析各自标准化和专业化,从而使得大型复杂结构只要能计算分析,就能同时进行优化;而方程(2)只有一个隐含条件F=0。

3 工程内点法EIPM与强化学习算法

最近一次优化理论的突破是内点法IPM(interion point method)[11]。根据大规模工程项目的特点,为求解方程(2),笔者对内点法做改进,创造性地提出了工程内点法EIPM(engineering interion point method)。

3.1 原理

工程内点法EIPM建立一个隐形的屏障(F=0)。当F=0即结构为合法设计时,优化问题为区域内的无约束优化问题。当F>0时,X越过了隐形屏障,通过修正X的求解方向使得X返回区域内。为了控制和管理隐形屏障,引入了机器学习的强化学习算法。通过强化学习和优化计算的结合,大大缩小计算时间,从而达到高效优化的效果。深入的技术原理另文论述。

3.2 主要算法描述

S0为初始状态,即在没进行优化前,结构的状态;Si为状态i,即第i步时结构状态;ai为行动i,即状态i时,所采取的行动,其为在状态Si时根据奖励值ri和Si采取的使最终的优化结果效果最好的行动;ri为奖励值i,即第i-1步时优化最后取得的成功的贡献值;B、H分别为节点截面的宽和高。

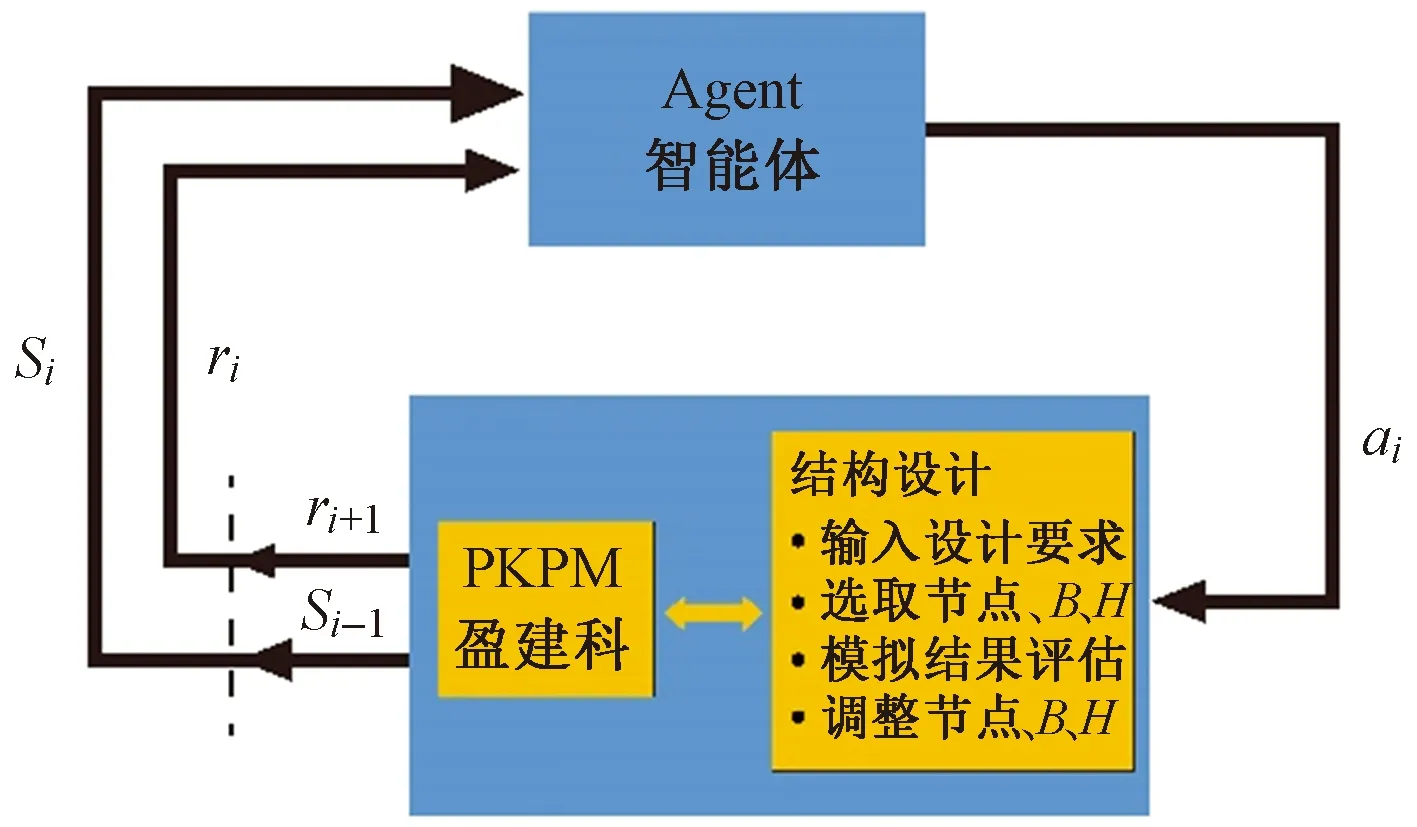
图1 强化学习流程图

工程内点法EIPM通过把优化过程转化为搜索过程,采用优化树搜索OPTS(optimization tree search)和保证结构安全的安全树搜索SCTS(safety control tree search)技术去控制和管理隐形屏障。OPTS是从数学的角度提供最优的搜索方向,SCTS是从工程的角度提供搜索方向。强化学习中的智能体根据当时的环境Si、奖励值ri、OPTS搜索方向pOPTS和SCTS搜索方向pSCTS形成强化学习ai[12-15]。

4 IBSO(S)软件系统介绍

根据上述技术原理,开发编制了大规模结构(钢结构)智能优化软件系统IBSO(S)(intelligent building structure optimization)(steel)。该软件系统是“AI结构师”V1.0软件系统的一部分,能在给定的建筑约束条件下,自动对钢结构计算分析的模型进行全杆件的成本优化。该系统已进行实际工程应用。优化流程见图2,IBSO(S)软件经过以下四个步骤对钢结构结构模型进行优化:

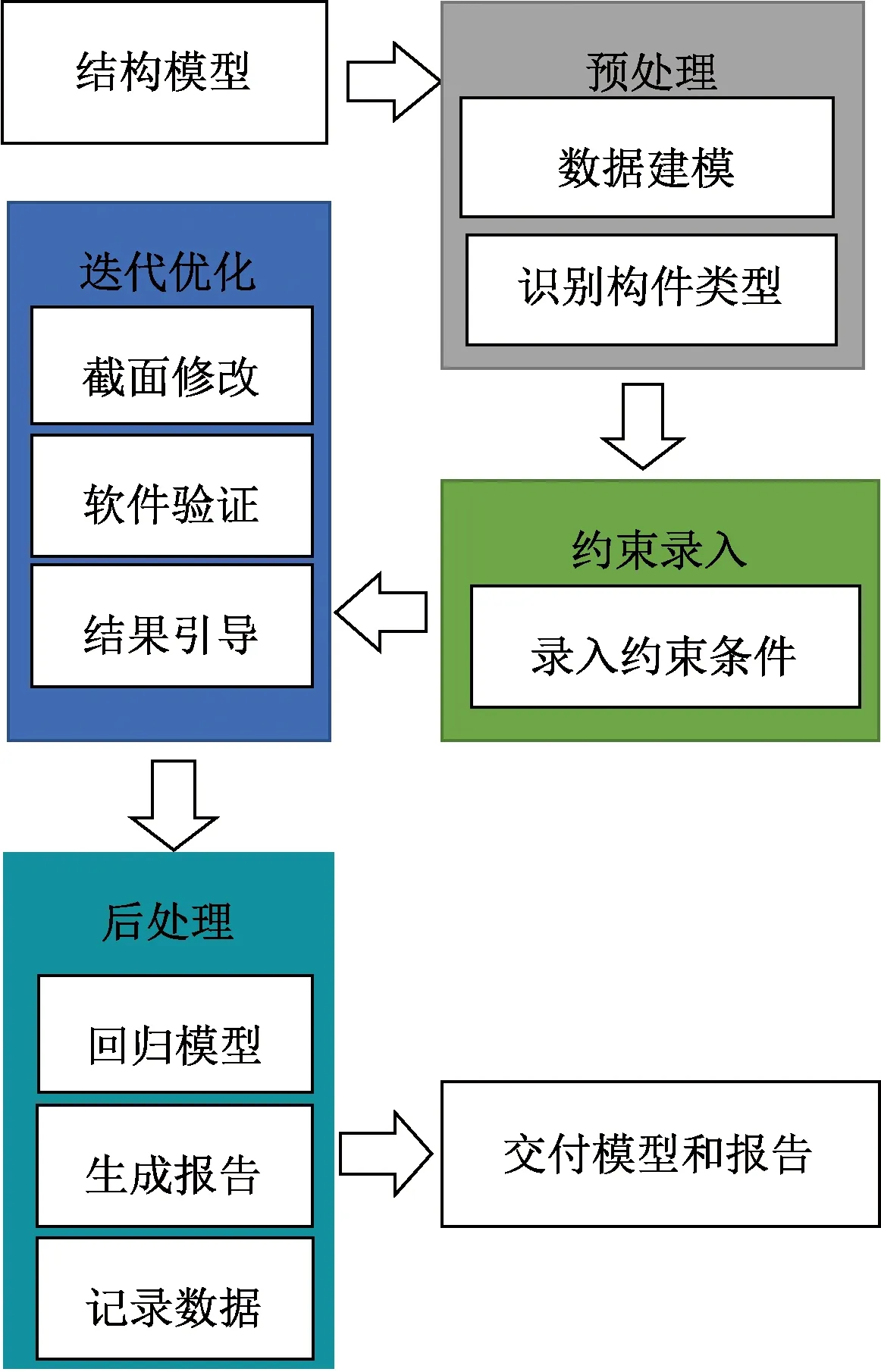
图2 优化流程图

(1)预处理:此步骤工作包括数据入库,完成数字化模型建模,识别构件类型,分析构件特性。以钢结构中工字梁为例,通过识别工字梁,完成腹板厚度b、总高度h、上翼缘宽度b1及厚度t1、下翼缘宽度b2及厚度t2等几何参数入库,作为优化变量。

(2)约束录入:通过文字约束条件自动转化成计算机识别约束,对已知构件进行约束控制,也可以通过特殊指定约束。

(3)迭代优化:根据约束和构件特性,通过自动化程序结合标准化计算分析软件的运行,完成模型每一个构件截面的智能选取。

(4)后处理:最终结果回归模型,并记录过程数据与结果数据,输出最终优化结果并呈现给客户。

5 钢结构智能优化的项目应用

5.1 项目一工程概况

海南“某项目1#楼”(简称1#楼),地下1层,地上15层,裙楼3层,地上部分为全钢结构,结构整体模型见图3。地上总建筑面积39326.32m2,建筑总高度70.6m,1～3层层高分别为6、5.5、5m,其余主要楼层层高均为4.5m。

图3 1#楼结构整体模型

建筑抗震设防类别为丙类,建筑结构安全等级为二级,抗震设防烈度为6度(0.05g),设计地震分组第一组,场地类别Ⅱ类,特征周期Tg=0.35s。基本风压为0.8kN/m2,地面粗糙度A类。1#楼1～4层的主要楼面恒载取1.5 kN/m2,活载取4.0kN/m2,4层以上(屋面除外)主要楼面恒载取1.2 kN/m2,活载取2.0kN/m2。

竖向构件取用方形钢管柱、方形或矩形钢管混凝土柱,钢材为Q355B。方形钢管柱的主要截面尺寸为(500～700)×(500～700)×(16～50),方形或矩形钢管混凝土柱的主要截面尺寸为(300～700)×(700～900)×(36～50),方形钢管混凝土强度等级为C50。主梁钢材为Q355B,主要截面有H900×300×16×28、H900×350×16×38、H800×300×16×32。主要楼层结构平面布置见图4、5。

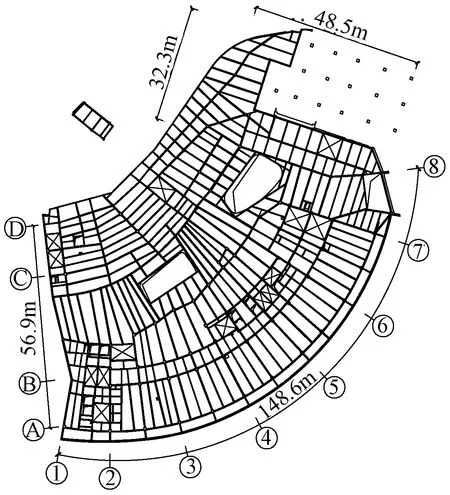
图4 1#楼2层塔楼平面布置

图5 1#楼8层塔楼平面布置图

5.2 项目二工程概况

项目二为多层商业建筑(简称“商业楼”),地下1层,地上4层,地上部分为全钢结构。地上总建筑面积为16603.16 m2,建筑总高度21.542m,1～3层层高均为6m。

建筑抗震设防类别为丙类,建筑结构安全等级为二级,抗震设防烈度为6度(0.05g),设计地震分组第一组,场地类别Ⅱ类,特征周期Tg=0.35s。基本风压为0.8kN/m2,地面粗糙度A类。2层～屋面层的主要楼面恒载取9、7.5、5、3kN/m2,主要楼面活载取3.5、3.5、2、0.5kN/m2。

竖向构件采用方形钢管柱及圆形钢管柱,钢材为Q355B。矩形钢管柱的主要截面尺寸为450×450×16、400×450×20、700×700×30,圆形钢管柱主要截面尺寸为φ450×20、φ1 500×30。主梁钢材为Q355B,梁的主要截面有HN650×300、HN630×200、HN700×300、HN450×150。总体模型见图6,2层结构平面布置见图7。

图6 商业楼结构整体模型

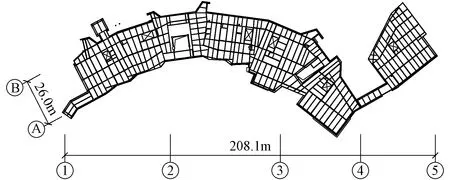
图7 商业楼2层结构平面布置图

5.3 优化策略

项目一、二均由设计院完成施工图设计后,甲方委托优化。结合项目特点及施工条件,在满足国家规范及建筑约束的要求下,优化方与设计院、施工单位及甲方充分沟通,四方达成以下四点共识:1)构件应力比普遍应在0.95以内,但允许少量在0.95～1之间;2)组合梁正弯矩计算及施工不涉及翼板有效宽度范围的纵向钢筋,可以简化设计及施工的相应工作;3)应有最小梁高及宽度以满足设计要求;4)结合施工意见及项目主要梁跨,综合决定需要做变截面梁的跨度。

故优化系统采用如下优化策略:1)90%的构件正应力强度与设计值比、稳定应力与设计值比、剪应力与设计值比不超0.95,余下10%的构件不超1。2)选择两端为铰接的次梁按组合梁考虑优化,并与按普通钢梁考虑优化的结果作比较,取最优值结果。3)假定H型截面最小梁高为350mm,最小上翼缘宽100mm、下翼缘宽150mm。方钢管最小高、宽均为300mm。4)对于跨度大于12m的梁,平均分三段,允许每一段的钢板厚度不相同。

5.4 优化前后对比

应用IBSO(S)软件系统,通过人机交互界面设定梁柱截面约束条件为高宽不大于原值,导入原设计计算模型(含几何数据、荷载数据、边界条件等),经软件运行后输出形成优化后的设计计算模型。

5.4.1 截面变化对比

优化后,项目一1#楼竖向构件采用方形钢管柱、方形或矩形钢管混凝土柱,钢材为Q355B。方形钢管柱的主要截面为(400～700)×(400～700)×(12～36);方形或矩形钢管混凝土柱的主要截面尺寸为(300～700)×(700～900)×(20～42),混凝土强度等级为C50。主梁钢材为Q355B,主要截面有H800×12×300×28、HN800×300、H900×350×16×38。

项目二商业楼竖向构件采用方形钢管柱及圆形钢管柱,钢材为Q355B。方形钢管柱的主要截面尺寸为450×450×16、400×450×20、450×450×14,圆形钢管截面尺寸为φ450×16、φ800×16。主梁钢材为Q355B,主要截面有H650×300×10×22、H650×200×10×16、HN400×200、H400×200×8×10。

在满足国家规范及约束条件的前提下,智能优化系统对全楼钢梁钢柱截面求更优解,并把更优解截面输出到设计软件(PKPM、盈建科等)以便设计师进一步验证。

5.4.2 性能指标对比

小震作用下整体模型性能计算结果见表1、2。由表1、2可知,优化后,1#楼的第1周期T1增大了约2.98%;抗剪承载力比提高了约5.26%;层间位移角X向增大约9.02%,Y向增大约16.21%。商业楼的第1周期T1增大了约5.99%;Y向抗剪承载力比降低了约8.21%;层间位移角X向增大约9.34%,Y向增大约13.54%。除Y向层间位移角外,各项指标前后相差不超10%,优化前后的计算结果较为接近,各项技术指标基本满足国家现行设计规范要求。

表1 1#楼小震优化前后分析结果对比

表2 商业楼小震优化前后分析结果对比

5.4.3 材料用量对比

优化前后的用钢量对比结果见表3、4。由表3可知,项目一的梁柱优化率均达到14.98%以上。除规范、建筑的约束外,另考虑了增加支撑的特定约束,综合优化率为13.1%。从表4可见,项目二商业楼,梁的优化率13.71%,柱为13.41%,综合优化率13.61%。上述最终优化设计分析结果满足国家现行设计规范及建筑要求,得到设计院认可和采纳。

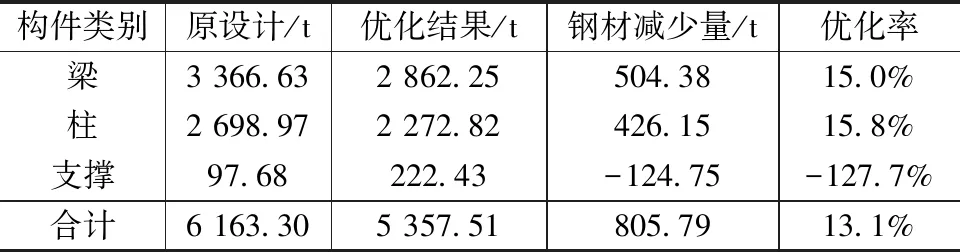
表3 1#楼小震优化前后用钢量对比

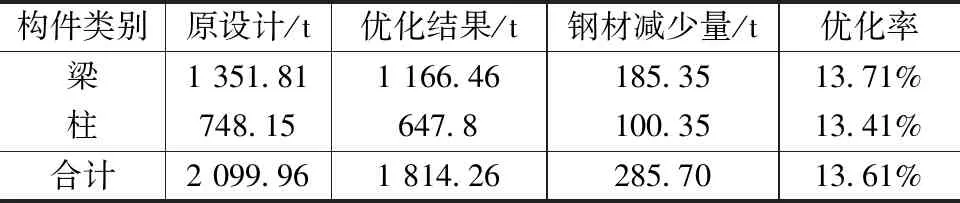
表4 商业楼小震优化前后用钢量对比

以上二个案例表明,由于优化参数和约束条件可以灵活增加,对大规模的钢结构项目可以实现有效优化。

6 结论

通过构建新型的结构优化模型(AI结构优化模型)和模型的智能求解技术,成功解决了超大规模钢结构成本更优化问题。所研发的IBSO(S)软件系统的应用表明,IBSO(S)设计经济性、合理性达到或超过人类结构设计工程师水平。整个智能优化全过程自动化操作,并且其结果可以直接应用到实际工程施工图。通常情况下,钢材用量优化率可达到10%以上。