投资者博彩偏好能否解释特质性波动率溢价之谜

陈晓辉 叶建华

【摘要】实证研究发现， 股价特质性波动率能负向预测股票收益率， 这与经典财务学假设相悖， 被称为特质性波动率溢价之谜。本文立足我国A股市场个体投资者众多、 博彩偏好明显及短期套利受限背景， 理论分析并实证检验投资者博彩偏好对该资产定价异象的解释力。研究结果表明， 特质性波动率溢价存在于A股市场， 同投资者博彩偏好密切相关的公司信息透明度及投资者风险感知对该资产定价异象具有负向调节作用， 且在投资者风险感知程度较高时期， 公司信息透明度对该资产定价异象的缓解作用减弱。

【关键词】投资者博彩偏好；风险感知；公司信息透明度；特质性波动率溢价之谜

【中图分类号】F275.5      【文献标识码】A      【文章编号】1004-0994（2023）16-0146-8

一、 引言

经典公司财务理论假设投资者足够理性并会在无摩擦市场中构建最充分资产组合分散掉特质性风险。这意味着投资者不用考虑资产特质性风险， 而只需考虑系统性风险， 特质性风险不具有资产定价效应。但越来越多的证据表明， 特质性风险仍具有资产定价效应， 这同投资者能构建充分多元化资产组合的假设相悖。此外， 即使投资者难以构建最充分多元化资产组合并需要承担特质性风险， 也会对承担的特质性风险要求正向溢价。但利用不同数据和估计方法， Ang等（2009）研究证明， 高特质性波动率股票会产生较低的收益率。 Guo和Savickas（2010）发现， 高特质性波动率股票的CAPM调整预期收益率较低。上述负向关系同投资者风险规避假设及传统理性资产定价理论相悖， 被称为特质性波动率溢价之谜。

后期研究主要围绕特质性波动率溢价之谜的存在性及其成因展开。近期研究认为特质性波动率溢价之谜的成因包括短期收益率反转（Huang等，2010）、 极端高收益率偏好（Bali等，2011）、 非对称性套利（Stambaugh等，2015）、 预期特质性偏度（Boyer和Vorkink，2014）及有限套利（Gu等，2018）。在我国A股市场， 短期收益率反转、 投资者彩票类偏好以及非对称性套利等因素均不能完全解释特质性波动率负向溢价（张华平和曹策远，2021）。

在我国A股市场中， 自然人投资者众多、 噪音交易行为普遍、 投资者博彩偏好强烈及短期卖空交易受限， 且与信息透明度密切相关的投资者博彩偏好会导致股价被高估。鉴于此， 本文立足我国A股市场实际， 从投资者风险感知和公司信息透明度影响投资者博彩偏好程度的视角， 探究投资者博彩偏好是否对特质性波动率溢价之谜具有解释力。本文不仅可丰富有关特质性波动率溢价之谜成因的研究， 还有助于加深对我国A股市场价格形成机制的理解。

二、 文献综述

（一）特质性波动率溢价之谜的存在性

近期许多研究致力于探究股价特质性波动率溢价之谜的存在性， 但并未达成共识。特质性波动率与预期收益率之间存在显著正向关系（Brown和Ferreira，2016）， 或没有界定任何精确关系（Wang等，2016）， 或存在负向关系（Shi等，2016）。其中， 特质性波动率与预期股票收益率之间存在显著负向关系被称为特质性波动率溢价之谜。Gu等（2018）验证了特质性波动率溢价之谜存在于中国股市， 并发现短期收益率反转、 彩票类股票偏好以及非对称性套利等观点并不能完全解释该资产定价效应。此后的研究证实了该发现， 但特质性波动率溢价之谜具有状态依赖性（陆静和张银盈，2022）。

（二）特质性波动率溢价之谜的成因

特质性波动率溢价之谜与标准金融理论假设投资者持有充分多元化资产组合及具有风险规避态度相悖， 致使标准金融理论难以解释这种关系（Merton， 1987）。近些年的研究试图从不同视角解释特质性波动率溢价之谜。

第一， 特质性波动率溢价之谜与特质性波动率的指标衡量方法有关。Jiang和Tian（2010）认为， 特质性波动率负向溢价的成因是波动率指标衡量的错误。Fu（2009）认为， Ang等（2009）构建的特质性波动率指标不能用于衡量时变的公司特质性风险。Fu（2009）用指数GARCH模型估计预期特质性波动率并发现条件特质性波动率溢价效应为正值。Brockman等（2022）的跨国研究证实， 采用Fu（2009）构建的预期特质性波动率指标产生了类似的结果。但Guo等（2014）利用模拟数据解释了这种偏差对预期特质性波动率和股票收益率关系的影响， 并发现该偏差能导致这种负向关系。Fink等（2012）及Guo等（2014）利用实际股票收益率数据研究发现， 股票收益率同样本外条件波动率预测值不存在任何关系。陆静和张银盈（2022）研究证明， 特质性波动率负向溢价来源于特质性波动率估计模型差异。

第二， 特质性波动率溢价之谜是公司主动对冲风险的结果。Grullon等（2012）认为， 特质性波动率变化与当前股票收益率正相关是特质性波动率溢价之谜的成因。特质性波动率变化都会增加公司成长期权价值， 但当公司对冲波动率增加时， 公司特质性风险会降低， 预期收益率下降。

第三， 特质性波動率溢价之谜是投资者极端高收益率偏好所致。Hai等（2020）证明， 在考虑最高日收益率资产定价效应后， 特质性波动率溢价之谜依然稳健存在， 说明这两种资产定价效应相互独立。Boyer等（2010）认为， 投资者并没有持有充分多元化的资产组合， 而会优先持有具备某些特征的股票。投资者常偏好持有具备彩票类特征的股票， 如预期破产概率（Ohlson，1980）、 预期失败概率（Campbell等，2008）、 预期特质性偏度（Boyer等，2010）、 上月份极端正向收益率（Bali等， 2011）以及预测的头奖概率（Conrad等，2014）。在这些刻画彩票类特征的代理变量中， Bali等（2011）证明， 在控制变量MAX（个股月度最高日收益率）后特质性波动率溢价之谜会消失。在欧洲， Annaert等（2013）的研究支持上述结果。但在中国股市特质性波动率溢价之谜不受MAX因素影响， 并主要存在于个体投资者持股比例较高的股票中（Fong和Toh，2014）。

第四， 投资者风险容忍度变化能一定程度上解释特质性波动率溢价。Qadan（2019）研究发现， 投资者风险容忍度提高时， 会从较安全股票转移至投机性更强的股票， 这对预期收益率与特质性波动率的关系产生强化效应。相反， 风险偏好降低会导致相反的结果。Shi等（2016）认为， 消息及情绪会影响特质性波动率与预期收益率的关系， 并发现控制好坏信息披露后， 特质性波动率溢价大幅下降。

第五， 卖空限制能一定程度上解释特质性波动率溢价之谜。Jiang等（2014）认为， 投资者过度自信及高套利成本限制使高特质性波动率股票收益率被高估， 导致特质性波动率与未来股票收益率之间呈负向关系。此外， 我国股市中限价交易制度及卖空限制制度可以限制套利者利用这些错误定价的机会（张华平和曹策远， 2021）。

（三）投资者博彩偏好对资产定价效应的影响

投资者博彩偏好具有重要的资产定价效应。投资者在选择资产时具有明显的偏好特征， 如本土情结（French和James，1991）、 小市值股偏好（Daniel等，1997）、 社会责任性投资偏好（Hong和Kacperczyk，2009）等。此外， 股市中投资者偏好低概率产生极端高收益率的股票（郑振龙和孙清泉，2013）， 彩票收益同股票收益具有诸多共同点， 投机行为会体现在股票投资中。Bali等（2011）研究证明， 股市中投资者具有博彩偏好。这意味着， 投资者愿意支付更高的价格购买此类股票。因此， 交易者可能高估彩票类股票， 导致此类股票产生负向未来收益率（Chen等，2019）。

投资者博彩偏好可解释一系列金融现象（叶建华，2017）。投资者博彩偏好可解释月度最高日收益率负向预测下月股票收益率现象（Cheon和 Lee，2018）、 REITS市场中的MAX效应（Zhu等，2020）、 A股市场中已实现峰度资产定价之谜（Chen等，2019）及彩票类股票的短期高收益率（叶建华，2017）。

（四）研究述评

综观上述文献可以发现： 第一， 特质性波动率溢价之谜普遍存在于发达及发展中股市， 但对其成因尚未达成共识。第二， 投资者博彩偏好普遍存在， 能解释多种资产定价异常。第三， 立足我国A股市场特殊背景， 探究投资者博彩偏好能否解释特质性波动率溢价之谜是重要的研究机会。

三、 理论分析与研究假设

（一）A股市场中特质性波动率溢价之谜的存在性

在我国特殊制度背景下， 特质性波动率溢价之谜存在于A股市场。第一， A股市场中投资者博彩偏好明显。据统计， 截至2023年6月底， 在A股市场开立账户的自然人和非自然人投资者数量分别为21840.54万户和50.99万户。我国已步入世界彩票销售大国， 居民博彩心理根深蒂固， 博彩偏好不断被强化（冯百鸣，2010）。郑振龙和孙清泉（2013）研究证明， A股市场中投资者具有博彩偏好， 投资基金也如此（向诚和杨俊，2021）。第二， 高特质性波动率股票具有彩票类特征。高特质性波动率股票符合博彩投资者对高收益率的偏好。根据累计前景理论， 投资者对资产收益率的尾部结果赋予较高权重， 高估小概率、 极端高回报率结果产生的概率， 提高此类股票估值（Barberis和Huang，2008）， 且投资者持有彩票类股票时会提高其效用水平并愿意为其支付高价（郑振龙和孙清泉，2013）。张金清和李建宇（2021）发现， 投资者博彩偏好提高了流动性风险溢价， 影响市场对上市公司未预期盈余的反应（陈文博和陈浪南，2021）。第四， A股市场中卖空限制会延缓资产被高估时的价值回归速度（吴蕾和部慧，2022）。A股市场中投资者博彩偏好会导致高特质性波动率股票收益率被高估， 并在未来收益率反转时产生负向溢价。基于此， 本文提出假设1。

假设1： 在我国A股市场中存在特质性波动率溢价之谜。

（二）投资者博彩偏好影响特质性波动率溢价之谜的理论分析： 基于公司信息透明度视角

高公司信息透明度可增加股价信息含量， 这会削弱投资者极端高收益率偏好对资产价格的影响。Foster（1981）认为， 公司信息透明度体现了市场对公司信息及所在行业信息的掌握程度， 信息透明度提高能增进市场效率。高信息透明度公司更可能引起投資者关注。相反， 不被市场和投资者广泛认知的股票更可能发生错误定价。此外， 在公司信息透明度较低时， 投资者非理性博彩偏好更加强烈（Choi等，2019）。高公司信息质量会减弱股市中盈余宣告后的价格漂移（杜妍和王生年，2021）、 极大日收益率效应（Zhu等，2020）并提高资产定价效率（郝亚绒和董斌，2022）。综上， 本文认为， 较低的公司信息透明度会加剧投资者博彩偏好， 特质性波动率负向溢价效应更明显， 反之则较弱。鉴于此， 本文提出假设2。

假设2： 在低信息透明度公司中， 投资者博彩偏好程度更高， 特质性波动率负向溢价效应更加明显。

（三）投资者博彩偏好影响特质性波动率溢价之谜的理论分析： 基于信息透明度和投资者风险感知双重视角

高投资者风险感知水平会削弱投资者博彩偏好对资产定价的影响， 并一定程度上替代公司信息透明度对特质性波动率负向溢价的影响。第一， 高投资者风险感知会强化投资者的风险管理政策和标准（Garleanu和Pedersen，2007）， 并加大投资者尤其是机构投资者融资约束（Brunnermeier等，2008）， 降低投资者市场参与度、 市场流动性及股价信息含量（Ma等，2019）。第二， 投资者风险感知会降低其风险承担水平及股票价格。高投资者感知风险水平的个股常具有更低的交易价格（王宗润和杨确，2020）及更高的公司资本成本（徐展等，2021）。

综上， 投资者风险感知水平较高时的风险承担水平下降， 市场对彩票类资产需求量及估值水平降低。投资者风险感知水平较高时对彩票类资产的偏好减弱， 致使具备彩票类特征的高特质性波动率股票的收益率高估程度降低甚至消失， 特质性波动率负向溢价水平较低。此外， 高投资者风险感知水平会抑制高特质性波动率股票收益率的高估程度， 进而替代公司信息透明度对高特质性波动率股票收益率高估程度的抑制作用。这意味着， 在投资者风险感知水平较高时， 公司信息透明度对特质性波动率负向溢价的削弱作用减弱。因此， 本文提出假设3和假设4。

假设3： 在投资者风险感知水平较高时， A股市场中的特质性波动率负向溢价水平降低。

假设4： 在投资者风险感知水平较高时， 公司信息透明度對特质性波动率负向溢价水平的削弱作用下降。

四、 研究设计

（一）样本设计

本文以1993 ～ 2021年A股市场所有上市公司为样本。股票交易数据来源于CSMAR数据库， 日、 月度三因子数据、 股票融资融券交易数据来源于RESSET金融研究数据库。剔除金融类公司、 极端值及数据缺失样本后， 最终有效样本观测值数量为341867个。

（二）主要变量设计

1. 被解释变量： 个股月度毛收益率。用Ri，t+1表示， 等于i股票在t+1月的实现收益率。

2. 解释变量： 股价特质性波动率。借鉴Ang等（2009）的方法， 估计t月i股票的特质性波动率（IVOLi，t）。

3. 调节变量。一是公司信息透明度。本文借鉴叶建华（2017）的方法， 在每个t月， 根据t-2月到t月个股日收益率及A股市场综合日收益率数据， 估计i股票在t月的公司信息透明度。二是投资者风险感知。风险感知对人的活动和决策有重要影响。人通常具有风险规避倾向， 风险感知水平较高时， 其从事风险行为的可能性较低。本文认为， 在A股市场， 市盈率低、 现金股利稳定的价值股风险相对较低， 而市盈率高、 现金股利存在很大不确定性的成长股风险相对较高。价值股资产组合同成长股资产组合间的收益率差异间接体现了投资者风险感知水平差异。鉴于此， 本文以t月价值股资产组合同成长股资产组合间的收益率差异IRPt-1衡量投资者风险感知水平， IRPt-1越大， 说明投资者风险感知水平越高， 反之则越低。衡量各月份投资者风险感知水平的具体计算方法如下： 第一， 基于t月初各股票的权益市账比从小到大的顺序把样本等分为4组， 并计算各资产组合在t月的收益率， 第1、 4组合的收益率分别用R1t和R4t表示。第二， 在每个t月用第4个组合收益率减去第1个组合收益率衡量t月投资者风险感知水平RPt。 RPt越大（越小）说明投资者风险感知水平越低（越高）。第三， 根据RPt把整个样本期间等分为投资者风险感知水平较低、 适中、 较高三个子样本期间。

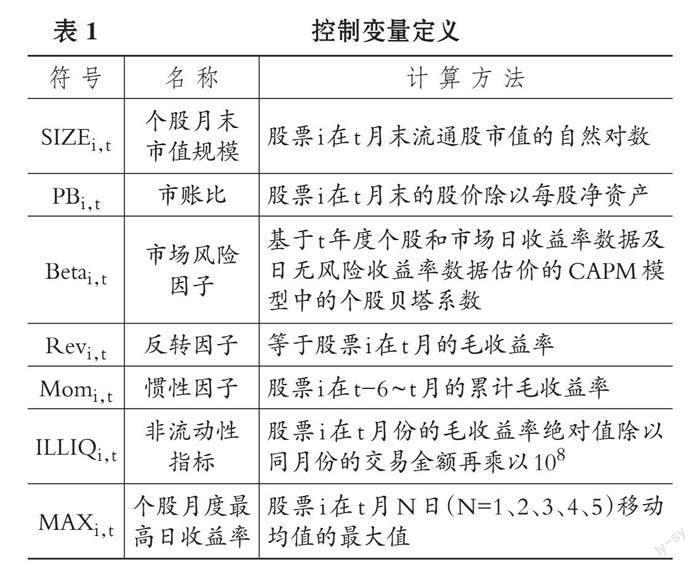
本文控制变量的定义如表1所示。

（三）实证模型设计

本文借鉴Qadan（2019）的研究设计模型（1）， 采用个人股层面数据， 按照Fama和MacBeth（1973）的方法估计模型（1）， 以证明特质性波动率溢价之谜是否存在。

Ri，t+1=β+β1IVOLi，t+β2SIZEi，t+β3PBi，t+

β4Betai，t+β5Revi，t+β6Momi，t+β7ILLIQi，t+β8MAXi，t+

εi，t-1 （1）

在模型（1）的基础上构建模型（2）检验公司信息透明度对特质性波动率负向溢价效应的影响。

Ri，t+1=β+β1Li，t+β2Hi，t+β3Li，t×IVOLi，t+β4Hi，t×IVOLi，t+β5IVOLi，t+β6SIZEi，t+β7PBi，t+β8Betai，t+

β9Revi，t+β10Momi，t+β11ILLIQi，t+β12MAXi，t+εi，t-1

（2）

在t月， 根据公司信息透明度， 将股票等分为低、 中、 高信息透明度三组样本， 用0、 1虚拟变量H和L分别表示高、 低信息透明度样本。

（四）描述性统计

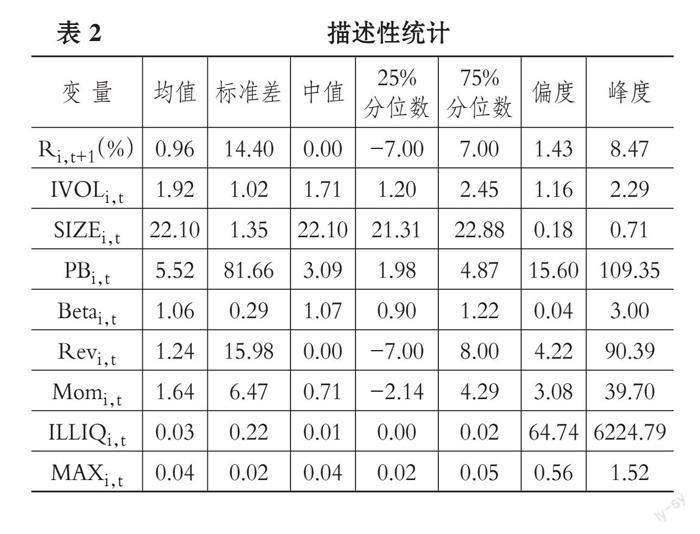
为避免异常值对实证结果的影响， 本文对具有较多异常值的变量Ri，t+1和PBi，t进行了1%和99%的缩尾处理。表2列示了主要变量的描述性统计结果。

五、 实证结果及分析

（一）资产组合收益率分析

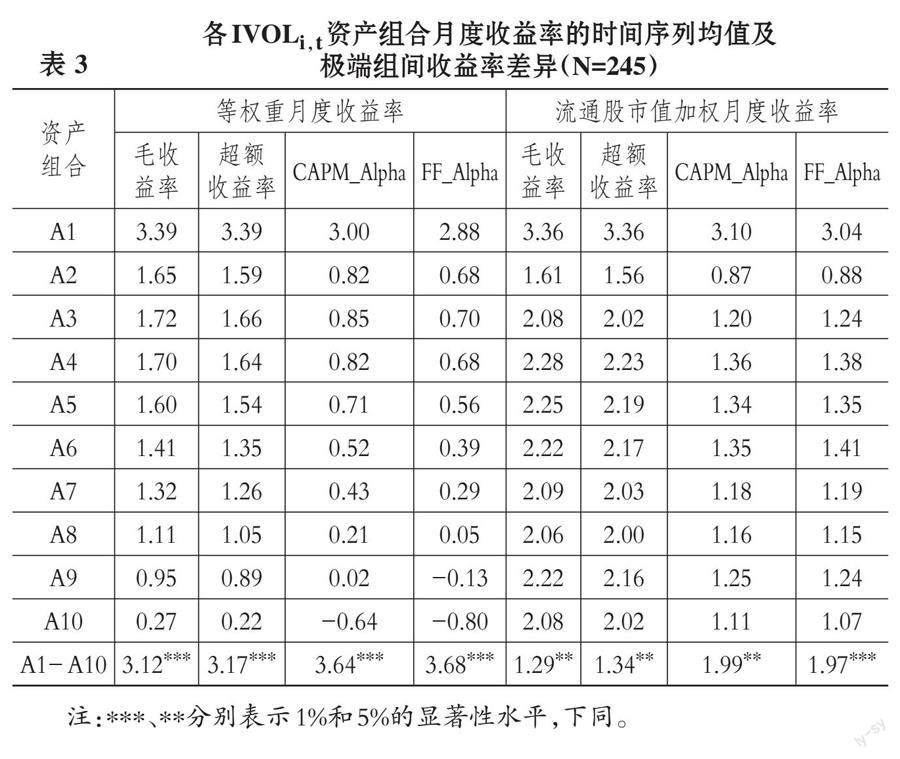
1. 基于IVOLi，t构建资产组合的收益率分析。第一， 在t月按照IVOLi，t从小到大排序并把样本等分为10组， IVOLi，t最小（最大）组用A1（A10）表示。第二， 计算t+1月各资产组合中个股月度毛收益率、 超额收益率的等权重和流通股市值加权收益率。第三， 计算样本期间各资产组合在t+1月（共245个月份）的各类收益率的时间序列均值。第四， 用t+1月个股超额收益率对同期市场超额收益率及三因子收益率进行时间序列回归， 估计截距项（资本资产定价模型调整资产组合风险收益率CAPM_Alpha和三因子调整资产组合风险收益率FF_Alpha）。第五， 对各资产组合间的CAPM_Alpha及FF_Alpha差异进行t检验。各资产组合的等权重及流通股市值加权的各类收益率及极端组间收益率差异如表3所示。

表3列示了按照IVOLi，t分组计算的各组的等权重及流通股市值加权的月度毛收益率、 超额收益率、 CAPM_Alpha及FF_Alpha的时间序列均值。从等权重收益率看， A1 ～ A10资产组合的毛收益率时间序列均值整体呈递减趋势， 两个极端资产组合A1和A10毛收益率时间序列均值的差异为3.12且在1%的水平上显著。A1 ～ A10资产组合的FF_Alpha及CAPM_Alpha均整体呈递减趋势， 两个极端资产组合A1和A10的FF_Alpha和CAPM_Alpha差异为3.68和3.64， 且均在1%的水平上显著。从流通股市值加权收益率看， A1 ～ A10资产组合的各收益率指标均呈明显递增趋势， 且两类收益率差异也均为正值并在1%的水平上显著。

资产组合收益率分析初步说明， 高特质性波动率资产组合未来期间的收益率显著低于低特质性波动率资产组合未来期间的收益率， A股市场中股票特质性波动率与未来股票收益率之间存在反向变动关系， 即特质性波动率溢价之谜存在于A股市场。

2. 基于公司信息透明度和IVOLi，t构建资产组合的收益率分析。第一， 在每个t月基于股价同步性（SYNi，t）从小到大的顺序把所有股票等分为3组。第二， 在t月的每個SYNi，t资产组合中基于IVOLi，t从小到大的顺序把该资产组合等分为10组， 这样构建了3×10个资产组合。第三， 计算每个t+1月各资产组合中个股的等权重及流通股市值加权月度收益率均值， 作为各资产组合在t+1月的收益率。第四， 计算样本期间各资产组合t+1月等权重及流通股市值加权收益率的时间序列均值。第五， 在整个样本期间， 分别以t+1月各资产组合等权重收益率和流通股市值加权收益率为被解释变量， 估计CAPM_Alpha及FF_Alpha。结果如表4所示。

资产组合收益率随着IVOLi，t增加而呈递减趋势。低、 中、 高信息透明度股票中， B1和B10的毛收益率差异分别为3.37、 2.36和1.01， 超额收益率差异分别为3.37、 2.36、 1.01， CAPM_Alpha差异分别为3.43、 2.51、 1.16， FF_Alpha差异分别为3.47、 2.56和1.20。这说明在控制公司信息透明度后， 随着IVOLi，t的增加， 股票预期收益率呈现递减趋势。

在低信息透明度股票中， 随着IVOLi，t的增加， 各资产组合收益率的递减趋势更明显。B1的毛收益率为3.68， 随后各资产组合的毛收益率单调递减， B10的毛收益率为0.31， 两个极端资产组合B1和B10的毛收益率差异为3.37且在1%的水平上显著。

在高信息透明度公司中， B1的毛收益率为0.92， 随后各资产组合的毛收益率并未单调递减， B10的毛收益率为-0.09， 两者差异为1.01且在5%的水平上显著。在低信息透明度公司中， B1、 B10资产组合的超额收益率、 CAPM_Alpha和FF_Alpha的差异均在1%的水平上显著， 且明显高于高信息透明度公司中的相应值。这说明， 在信息透明度较低（高）的公司中， 特质性波动率负向溢价效应更加明显（较弱）。

基于与表4类似的方法， 按照公司信息透明度和IVOLi，t构建各类流通股市值加权月度收益率的时间序列均值及极端组间的差异（限于篇幅结果未列示）。在低信息透明度公司中， B1和B10的毛收益率、 超额收益率、 CAPM_

Alpha及FF_Alpha差异分别为1.81、 1.81、 1.83和3.47， 且分别在5%、 5%、 5%和1%的水平上显著。在中信息透明度公司中， B1和B10的毛收益率、 超额收益率、 CAPM_Alpha及FF_Alpha差异分别为0.16、 0.16、 0.51和2.56， 且除2.56在1%的水平上显著外， 其他收益率差异均不显著。在高信息透明度公司中， B1和B10的毛收益率、 超额收益率、 CAPM_Alpha及FF_Alpha差异分别为-0.24、 -0.24、 0.07和1.20， 且分别在5%、 5%、 5%和1%的水平上显著。这说明， 特质性波动率负向溢价存在于低信息透明度公司中， 而在高信息透明度公司中并不显著。

上述分析结果证明特质性波动率负向溢价之谜存在于我国A股市场中， 且在低信息透明度公司中最为显著， 而在高信息透明度公司中并不显著。

（二）回归分析

1. 特质性波动率负向溢价效应存在性。表5列示了整个样本期间模型（1）的Fama和MacBeth（1973）分步逐月横截面回归结果。在第三、 四步回归结果中， MAXi，t的斜率为-16.54和14.18且均在1%的水平上显著。这说明A股市场存在Bali等（2011）发现的最高日收益率资产定价效应， 但引入IVOLi，t后， MAX效应被显著逆转。这意味着A股市场中， 特质性波动率效应是一种真正的资产定价效应， 而MAX效应只是特质性波动率效应的一种特殊形式。在第三步基础上引入IVOLi，t后， 模型拟合优度从10.81%增加至11.71%， 说明IVOLi，t对预期股票收益率有非常明显的解释力。

上述回归结果充分说明， 在A股市场中， 控制主要收益率预测变量后， 股价特质性波动率能够显著负向预测未来股票收益率， 特质性波动率负向溢价效应存在于A股市场， 且该效应能够替代MAX效应， MAX效应并非真实的资产定价效应。

2. 公司信息透明度对特质性波动率溢价之谜的影响。表6列示了整个样本期间模型（2）的Fama和MacBeth（1973）分步逐月横截面回归结果。

从表6可以看出， 各步回归结果中L（H）的斜率均显著为正（负）。这说明低信息透明度公司股票的预期收益率显著高于高信息透明度公司， A股市场中可能存在与信息透明度相关的风险溢价。第一步回归结果中， L×IVOLi，t的斜率为-0.28且在5%的水平上显著， IVOLi，t的斜率为-1.23且在1%的水平上显著。第二步回归结果中， H×IVOLi，t的斜率为0.28且在5%的水平上显著， IVOLi，t的斜率为-1.36且在1%的水平上显著。第三步回归结果中， L×IVOLi，t的斜率为-0.15但不显著， H×IVOLi，t的斜率为0.34且在1%的水平上显著， IVOLi，t的斜率为-1.70且在1%的水平上显著。这些证据表明， 同高信息透明度公司相比， 特质性波动率负向溢价效应显著存在且在信息透明度较低的公司中更显著。

回归结果证明， 特质性波动率溢价之谜存在于我国A股市场， 且该资产定价效应在低（高）信息透明度公司中更明显（偏弱）。因此， 样本整体的回归结果再次证实了假设1和假设2。

3. 投资者风险感知、 信息透明度对特质性波动率负向溢价的影响。在投资者风险感知水平较低、 适中及较高样本期间， 按照表6的分步回归步骤估计模型（2）的Fama和MacBeth（1973）横截面回归结果（限于篇幅，估计结果未列示）。结果表明， 在投资者风险感知水平低、 中、 高子样本期间， 第三步回归结果中H的斜率分别为-2.67、 -1.47和-1.56且均在1%的水平上显著， L的斜率分别1.17、 0.60和1.87， 且1.17和1.87分别在5%和1%的水平上显著。上述结果说明， 在投资者风险感知水平较低（较高）的样本期间， 高信息透明度公司的预期收益率较低（低信息透明度公司的预期收益率较高）。这意味着， 在投资者风险感知水平较低（较高）时， 投资者会降低（提高）对承担信息透明度风险要求的收益率补偿。

在投资者风险感知水平低、 中、 高子样本期间， 第三步回归结果中， IVOLi，t的斜率分别为-1.97、 -1.45和-1.72且均在1%的水平上显著， 这说明投资者风险感知水平较低及较高的样本期间， 特质性波动率负向溢价效应更加明显， 这意味着在投资者风险感知水平较低及较高时， 投资者对特质性波动率相关的极端高收益率的偏好均可能更强， 极端的投资者风险偏好水平会加剧特质性波动率的负向溢价效应。这些证据部分证明了假设3。

在投资者风险感知较低期间， H×IVOLi，t的斜率分别为0.25和0.67且均在5%的水平上显著， 在其他期间， H×IVOLi，t的斜率均为正值但不显著。这说明， 高信息透明度整体上减弱了特质性波动率负向溢价效应， 并且这种减弱作用在投资者风险感知水平较低期间最为明显， 在投资者风险感知水平较高期间偏弱， 这证明了假设2和假设4。

在投资者风险感知水平较低、 适中和较高期间， 第二步回归结果中L×IVOLi，t的斜率分别为-0.37（在10%的水平上显著）、 -0.07（不显著）和-0.40（在1%的水平上显著）， 第二步回归结果中L×IVOLi，t的斜率均不显著。这说明， 低公司信息透明度整体上强化了特质性波动率负向溢价效应， 且这种效应在投资者风险感知较高（较低）期间更明显（较弱）， 这也证明了假设2和假设4。

综上所述， 在投资者风险感知水平较低（较高）时， 投资者对承担信息透明度风险要求的收益率补偿较低（较高）。较高和较低的投资者风险感知水平均会强化投资者极端高收益率偏好， 特质性波动率负向溢价效应更加明显。较高的信息透明度整体上会减弱特质性波动率负向溢价效应， 并且这种影响在投资者风险感知水平较低期间最为明显。

六、 结语

本文以我国A股上市公司为样本， 采用资产组合收益率分析和回归分析方法， 实证检验了特质性波动率溢价之谜的存在性及与投资者博彩偏好相关的信息透明度和投资者风险感知是否对该资产定价异象具有解释力。实证结果表明： 特质性波动率溢价之谜存在于我国A股市场。低（高）信息透明度公司的博彩偏好更强烈（较弱）， 特质性波动率负向溢价效应更显著（较弱）。投资者风险感知水平较低时博彩偏好更强， 特质性波动率負向溢价效应更明显。投资者风险感知对特质性波动率溢价的抑制作用一定程度上替代了信息透明度对该资产定价异象的抑制作用。本研究从公司信息透明度和投资者风险感知视角， 间接证明了投资者博彩偏好对特质性波动率溢价之谜具有一定解释力， 提供了投资者博彩偏好影响资产定价的确凿证据， 丰富了有关特质性波动率溢价之谜存在性及成因研究， 为破解行为财务学研究中投资者认知、 心理及行为偏差不易识别和衡量的难题提供了新的思路和方法。

本研究的现实启迪意义体现在三个方面。第一， 有助于非理性投资者纠正博彩偏好及聪明投资者利用这种错误定价机会， 提高投资者投资收益及股市定价效率。第二， 上市公司提高信息透明度有助于抑制投资者博彩偏好， 进而降低公司外部融资成本及提高企业价值。第三， 监管机构不仅需要注重对上市公司信息披露的监管， 还应注重对市场投资者风险观念的正确引导， 这有助于提高资本市场定价效率和降低资本市场系统性风险。

【 主 要 参 考 文 献 】

陈文博，陈浪南．股市投资者对盈余公告的反应 —— 基于博彩偏好的视角［ J］．中国管理科学，2021（9）：1 ～ 11．

杜妍，王生年．提高会计信息可比性缓解了股价漂移吗？［ J］．管理学刊，2021（1）：81 ～ 98．

冯百鸣．彩票消费与宏观经济相关性的实证研究［ J］．经济经纬，2010（4）：25 ～ 29．

郝亚绒，董斌．A股纳入MSCI指数改善中国资本市场定价效率了吗？［ J］．世界经济研究，2022（7）：76 ～ 89+136 ～ 137．

陆静，张银盈．“特质波动率之谜”与估计模型有关吗？［ J］．中国管理科学，2022（9）：36 ～ 48．

吴蕾，部慧．卖空机制效率评价：基于金融系统工程视角的状态空间方法［ J］．管理评论，2020（7）：326 ～ 336．

王宗润，杨确．性别和风险感知对投资行为的影响 —— 基于行为实验室实验的数据［ J］．湘潭大学学报（哲学社会科学版），2020（3）：123 ～ 130．

向诚，杨俊．谁在市场中赌博？基金博彩行为研究［ J］．中国管理科学，2021（11）：224 ～ 236．

徐展，盛思思，顾奋玲．关键审计事项、风险感知与权益资本成本［ J］．金融经济学研究，2021（5）：133 ～ 147．

叶建华．投资者情绪、公司信息透明度与股市极大日收益率效应 —— 基于中国A股市场的经验证据［ J］．投资研究，2017（7）：113 ～ 126．

张华平，曹策远．有限套利是否影响股价特质性波动率的资产定价效应［ J］．管理科学，2021（4）：149 ～ 160．

张金清，李建宇．博彩性投机行为会影响流动性风险溢价吗？［ J］．东南大学学报（哲学社会科学版），2021（3）：53 ～ 64+147．

郑振龙，孙清泉．彩票类股票交易行为分析：来自中国A股市场的证据［ J］．经济研究，2013（5）：128 ～ 140．

Ang A.， Hodrick R. J.， Xing Y.， et al.. High idiosyncratic volatility and low returns：International and further U.S. evidence［ J］．Journal of Financial Economics，2009（1）：1 ～ 23．

Annaert J.， Ceuster M. D.， Verstegen K.. Are extreme returns priced in the stock market？ European evidence［ J］．Journal of Banking & Finance，2013（9）：3401 ～ 3411．

Bali T. G.， Cakici N.， Whitelaw R. F.. Maxing out：Stocks as lotteries and the cross-section of expected returns［ J］．Journal of Financial Economics，2011（2）：427 ～ 446．

Barberis N.， Huang M.. Stocks as lotteries： The implications of probability weighting for security prices［ J］．American Economic Review，2008（5）：2066 ～ 2100．

Boyer B. H.， Vorkink K.. Stock options as lotteries［ J］．The Journal of Finance，2014（4）：1485 ～ 1527．

Brockman P.，  Guo T.，  Vivero M. G.， Yu W.. Is idiosyncratic risk priced？ The international evidence［ J］．Journal of Empirical Finance，2022（66）：121 ～ 136．

Brown D. P.， Ferreira M. A.. Idiosyncratic volatility of small public firms and entrepreneurial risk［ J］．Quarterly Journal of Finance，2016（1）：1 ～ 59．

Brunnermeier M. K.， Nagel S.， Pedersen L. H.. Carry trades and currency crashes［ J］．NBER Macroeconomics Annual，2008（1）：313 ～ 348．

Campbell J. Y.， Hilscher J.， Szilagyi J.. In search of distress risk［ J］．The Journal of Finance，2008（6）：2899 ～ 2939．

Chen G.， Ding J.， Zhao X.. A lottery-preference-based explanation of realized kurtosis puzzle in Chinese stock market［ J］．Applied Economics，2019（50）：5466 ～ 5481．

Cheon Y. H.， Lee K. H.. Maxing out globally： Individualism， investor attention， and the cross section of expected stock returns［ J］．Management Science， 2018（12）：5807 ～ 5831．

Conrad J.， Kapadia N.， Xing Y.. Death and jackpot： Why do individual investors hold overpriced stocks？［ J］．Journal of Financial Economics，2014（3）：455 ～ 475．

Daniel K.， Grinblatt M.， Titman S.， Wermers R.. Measuring mutual fund performance with characteristic-based benchmarks［ J］．The Journal of Finance， 1997（3）：1035 ～ 1058．

Fama E. F.， MacBeth J. D.. Risk， return， and equilibrium： Empirical tests［ J］．Journal of Political Economy，1973（3）：607 ～ 636．

Fink J. D.， Fink K. E.， He H.. Expected idiosyncratic volatility measures and expected returns［ J］．Financial Management，2012（3）：519 ～ 553．

Fong W. M.， Toh B.. Investor sentiment and the MAX effect［ J］．Journal of Banking and Finance，2014（46）：190 ～ 201．

Foster G.. Intra-industry information transfers associated with earnings releases［ J］．Journal of Accounting and Economics，1981（3）：201 ～ 232．

French K. R.， James M P.. Investor diversification and international equity markets［ J］．American Economic Review，1991（2）：222 ～ 226．

Fu F.. Idiosyncratic risk and the cross-section of expected stock returns［ J］． Journal of Financial Economics，2009（1）：24 ～ 37．

Garleanu N.， Pedersen L. H.. Liquidity and risk management［ J］．American Economic Review，2007（2）：193 ～ 197．

Grullon G.， Lyandres E.， Zhdanov A.. Real options， volatility， and stock returns［ J］．The Journal of Finance，2012（4）：1499 ～ 1537．

Gu M.， Kang W.， Xu B.. Limits of arbitrage and idiosyncratic volatility： Evidence from China stock market［ J］．Bank Finance，2018（86）：240 ～ 258．

Guo H.， Kassa H.， Ferguson M. F.. On the relation between EGARCH idiosyncratic volatility and expected stock returns［ J］．Journal of Financial and Quantitative Analysis，2014（1）：271 ～ 296．

Guo H.， Savickas R.. Relation between time-series and cross-sectional effects of idiosyncratic variance on stock returns［ J］．Journal of Banking and Finance，2010（7）：1637 ～ 1649．

Hong H.， Kacperczyk M.. The price of sin： The effects of social norms on markets［ J］．Journal of Financial Economics，2009（1）：15 ～ 36．

Huang W.， Liu Q.， Rhee S. G.， Liang Z.. Return reversals， idiosyncratic risk， and expected returns［ J］．The Review of Financial Studies，2010（1）：147 ～ 168．

Jiang D.， Peterson D. R.， Doran J. S.. Short-sale constraints and the idiosyncratic volatility puzzle： An event study approach［ J］．Journal of Empirical Finance，2014（28）：36 ～ 59．

Jiang G. J.，  Tian Y. S.. Misreaction or misspecification？ A re-examination of volatility anomalies［ J］．Journal of Banking and Finance，2010（10）：2358～2369．

Merton R. C.. A simple model of capital market equilibrium with incomplete information［ J］．The Journal of Finance，1987（3）：483 ～ 510．

Ohlson J. A.. Financial ratios and the probabilistic prediction of bankruptcy［ J］．Journal of Accounting Research，1980（18）：109 ～ 131．

Qadan M.. Risk appetite， idiosyncratic volatility and expected returns［ J］．International Review of Financial Analysis，2019（65）：101372．

Shi Y.， Liu W. M.， Ho K. Y.. Public news arrival and the idiosyncratic volatility puzzle［ J］．Journal of Empirical Finance，2016（37）：159 ～ 172．

Stambaugh R. F.， Yu J.， Yuan Y.. Arbitrage asymmetry and the idiosyncratic volatility puzzle［ J］．Journal of Finance，2015 （5）：1903 ～ 1948．

Wang L. H.， Lin C. H.， Kang J. H.， Fung H. G.. Idiosyncratic volatility and excess return： Evidence from the greater China region［ J］．Finance Research Letters，2016（19）：126 ～ 129．

Zhu Z.， Harrison D. M.， Seiler M. J.. Preference for lottery features in real estate investment trusts［ J］．International Review of Economics and Finance，2020（69）：599 ～ 613．