基于图像处理的跳频信号参数估计和双网台分选*

王宇阳，黄 浩，陶建军

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

无论是跳频通信的干扰技术中的阻塞式干扰的设计，还是跳频通信的干扰技术中的瞄准式干扰的设计，抑或是搭载跳频通信单元的敌方侦察无人机的干扰与反制的实际场景中，如果在干扰之前能够获得部分（甚至全部）的敌方跳频信号的跳频参数，如跳时、跳速、跳频周期，以及每一跳的驻留时间[1-2]，甚至是时频域内的跳频图案或跳变规律，那么我方干扰机就可以根据敌方跳频信号的跳频参数的这些先验知识进行针对性的干扰，这样就可以大大提高我方干扰机的干扰效率和干扰成功率。另外，随着跳频通信技术的发展，在实际对跳频通信进行干扰的过程中往往会遇到多个跳频网台，多网台抗干扰能力很强，任何干扰机都无法直接对多网台的跳频信号进行干扰，这就需要对多网台进行分选，分选出特定的需要干扰的网台进行针对性的干扰。因此，可以看出参数估计和网台分选在干扰跳频信号过程中的重要性，接下来本文将在第2 节和第3 节中对跳频信号的参数估计和网台的分选进行深入的研究。

跳频通信的跳频信号具有非平稳的随机特性，并且它的频率会根据伪随机序列码进行快速转换。为了分析非平稳信号的详细特征，可以使用时间频率分析的方法。因此，针对跳频信号参数估计问题，可以通过时频分析的方法来分析某一时刻的跳频信号的频谱信息[3]。传统的时频分析方法包括伪魏格纳分布（Pseudo Wigner-Ville Distribution，PWVD）[4]、光滑的伪魏格纳分布（Smooth Pseudo Wigner-Ville Distribution，SPWVD）[5-6]、短时傅里叶变换（Short-Time Fourier Transform，STFT）[7]、魏格纳分布（Wigner-Ville Distribution，WVD）[8-9]、小波变换，等等。

近年来，一些信号检测和感知的方法被广泛应用于物联网与通信领域[10-14]。物联网与智能感知实验室（Internet of Things and Intelligent Sensor Laboratory，IOTS Lab）的智能感知信号研究小组成员近几年在跳频信号处理领域取得了一定的进展[15-17]。他们在分布式调制带宽转换器（Distributed Modulated Wideband Converter，DMWC）采样和恢复框架下，通过时频脊线图的方法来估计跳频信号的跳时、跳速、跳频周期等跳频参数，这种稀疏重构的方法是目前最主流的跳频信号参数估计方法。然而，这种主流的跳频信号参数估计方法并不能估计跳频信号的瞬时带宽，因此该实验室研究小组成员[18]又从另一个图像处理的角度来估计跳频信号的跳时、跳速、跳频周期等参数。特别的是，这种利用图像处理来估计跳频信号的参数的方法可以估计出跳频信号的瞬时带宽参数，这是以前的主流方法无法做到的。此外，因为该方法特别适合于时频图是分离的情况，所以该方法与原来的方法相比适用性更广。它不仅可以用于识别跳频信号，而且可以用于识别频谱分离的各种类型的信号。另外，原来的主流方法不适用于多网台的跳频信号的参数估计，但这种新方法更适用于多网台的跳频信号的参数估计。

在以上方法的基础上，本文针对基于图像处理的跳频信号参数估计和网台分选中去除噪声的问题，提出了对应的自适应定门限二分聚类算法，大大提高了对多网台的跳频信号在噪声环境下的参数估计精度和网台分选成功率。

1 自适应定门限二分聚类算法

图1（a）～（f）分别为迭代过程的分步图解，x轴表示实轴，单位为+1；y轴表示虚轴，单位为+j。图1（a）中灰色的点表示采样点。图1（b）中人为选择一个初始信号类聚中心用灰叉表示，人为选择一个初始噪声类聚中心用黑叉表示。如果其中一个采样点到信号类聚中心的距离比该采样点到噪声类聚中心的距离近，那么将该采样点归为信号类并且将该采样点改成灰色。反之，将该采样点归为噪声类并且将该采样点改成黑色，于是就得到了图1（c）。通过图1（c）求出标为灰色的采样点的重心，接着将该重心更新为新的信号类聚中心并用灰叉表示。求出标为黑色的采样点的重心，接着该重心更新为新的噪声类聚中心并用黑叉表示，于是就得到了图1（d）。图1（d）中如果其中一个采样点到信号类聚中心的距离比该采样点到噪声类聚中心的距离近，那么将该采样点归为信号类并且将该采样点改成灰色。反之，将该采样点归为噪声类并且将该采样点改成黑色，于是就得到了图1（e）。图1（e）重复前面的步骤就得到了图1（f）。如果将上述过程只显示一个结果，那么就如图1（g）所示。

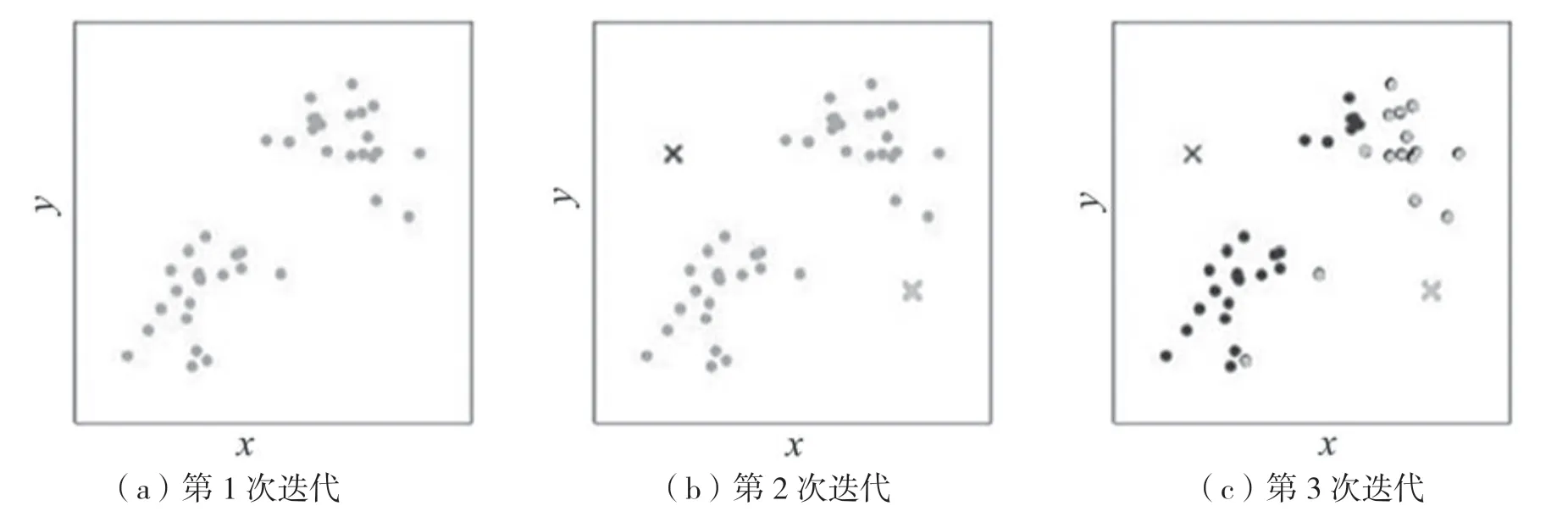
图1 复数域内自适应定门限二分聚类算法的迭代过程

复数域内自适应定门限二分聚类算法的效果如图2 所示，图中，x轴表示实轴，单位为+1；y轴表示虚轴，单位为+j。假设图2 为对跳频信号进行采样后获得的复数域内的原始数据，其中包含了跳频信号和噪声信号两类采样点数据，经过多次迭代，通过聚类将跳频信号数据和噪声数据分离开来了，并分别获得跳频信号和噪声信号的聚类中心。

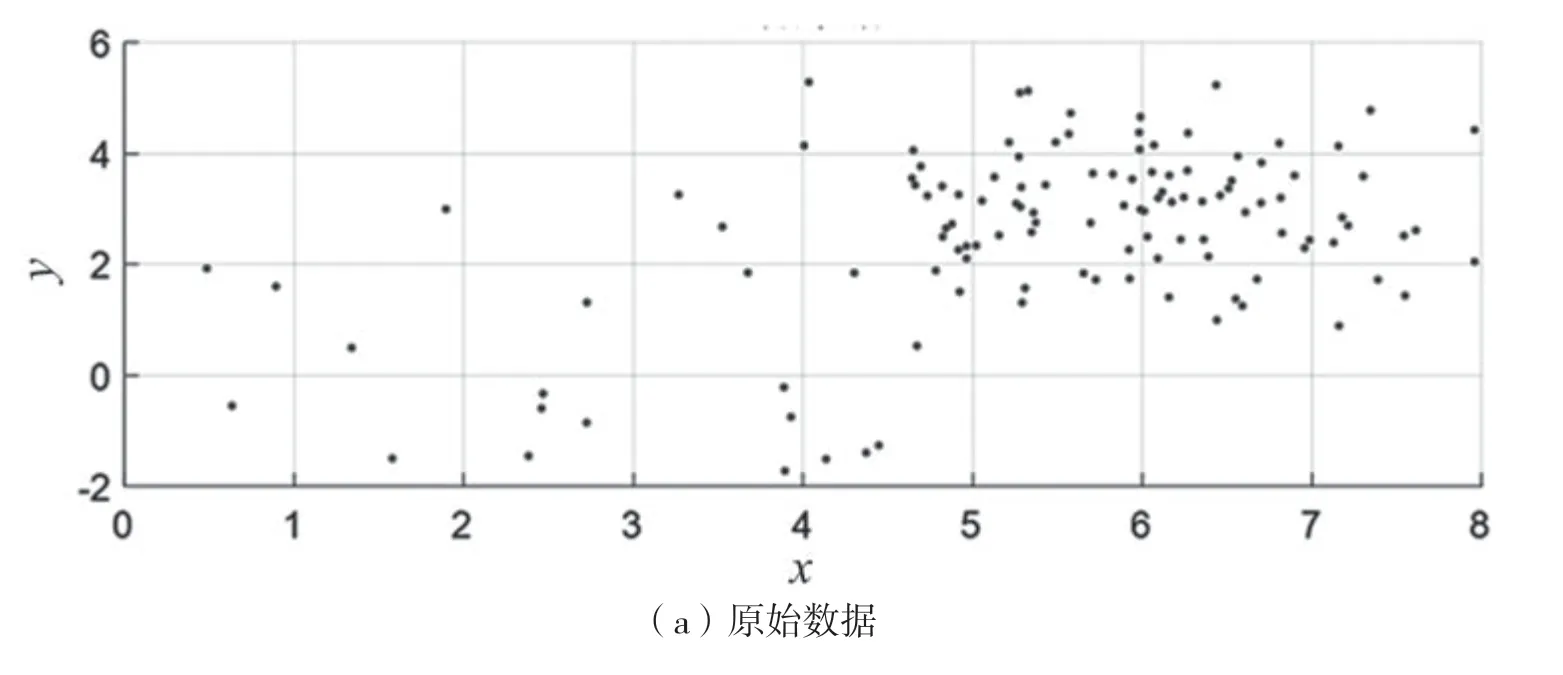
图2 复数域内自适应定门限二分聚类算法效果

对图2 中复数域内的采样点数据的每个点求模值，就可以得到每个采样点数据的图像中的灰度值，并且将所有的灰度值标在坐标轴上，那么就可以得到图3。图中，x轴表示图像中的灰度值，单位为+1；y轴没有含义且无单位。

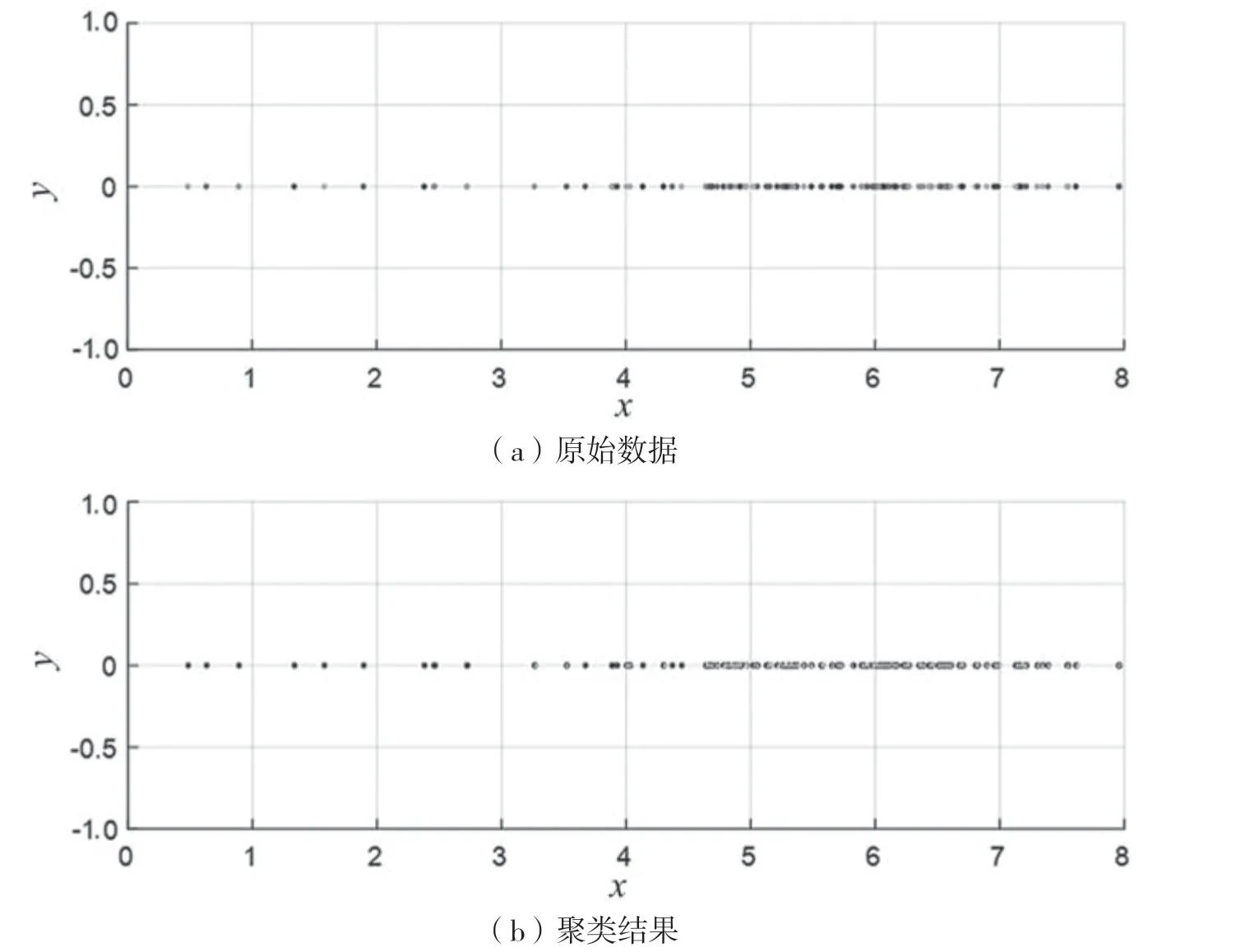
图3 自适应定门限二分聚类算法效果

首先要明确的是，本文在时频图中把所有点的灰度值作为分类的对象，此时可以把信号和噪声的值作为两个类别，分别为信号类和噪声类。在自适应定门限二分聚类算法中，两个初始点本来可以随机选取的，但通过多次随机取两个初始点的值验证可以发现，取噪声类的初始点为灰度值的最低点且信号类的初始点为灰度值的最高点。这样经过自适应定门限二分聚类以后，就能更加快速和精确地将信号和噪声分离，即找到信号的聚类中心为L1，噪声的聚类中心为L2，则可设置修正门限为th2=(L1+L2)/2。在时频图中把小于门限的灰度值置为0，大于或等于门限的灰度值保留[19]。这个过程中最关键的是通过自适应定门限二分聚类算法找到不同信噪比下对应的不同的门限值th2，这样才能完成在不同信噪比下的去噪过程。这样自适应地确定不同信噪比下对应的不同的门限值，其实就是自适应地对不同强弱的噪声进行针对性的去噪，大大提高了去噪的效果。这里的自适应也就是自动地确定门限，这是本算法最核心的创新点。

如图4 所示，在信噪比为-2 dB 时，将两个网台的跳频信号组网，x轴表示时间，单位为s；y轴表示频率，单位为Hz。将第1 个网台的跳频信号的每一跳的驻留时间设置为第2 个网台的跳频信号的每一跳的驻留时间的两倍，然后生成两个网台的跳频信号的时频瀑布图，如图4（a）所示。接着将两个网台的跳频信号通过自适应定门限二分聚类算法进行去噪处理后再生成时频瀑布图，这样就按照图像灰度值的大小将两个网台的跳频信号与环境中的噪声分离开了，然后将分离出来的两个网台的跳频信号的灰度值乘1，再将分离出来的环境噪声信号的灰度值乘0，得到图4（b）。那么，经过自适应定门限二分聚类算法去噪后得到的两个网台的跳频信号的时频瀑布图就比未经过自适应定门限二分聚类算法去噪的两个网台的跳频信号的时频瀑布图更加清晰和准确。该处理过程为后续的图像处理做好了前期准备。

图4 多网台的跳频信号时频图去噪前后对比

2 基于图像处理的跳频信号参数估计

本文所使用的图像处理的单次多重检测器（Single Shot MultiBox Detector，SSD）检测框架是通过Python 源代码实现的，并且可以通过康奈尔大学的开源许可证在其官网上获得[20]。2017 年，Ren 等人[21]和Girshick 等人[22]提出了快速区域卷积神经网络（Fast Region-based Convolutional Neural Networks，Fast RCNN）检测框架，显著提高了RCNN 检测框架的识别精度和识别速度。为了解决RCNN 生成候选区域的一系列问题，Redmon 等学者[23]提出了YOLO 目标监测框架。2016 年，Liu 和Anguelov 等学者提出了SSD 检测框架，该框架不但采用了Fast RCNN 的锚定机制，而且继承了YOLO的回归策略[24]。SSD 检测框架的主要思想是利用卷积核对不同尺寸特征图上的检测目标的类型和偏移坐标进行预测，大大提高了目标检测的精度和实时性[25]。SSD 检测框架模型基于多盒目标理论，可以用于训练多个目标[26-28]。

通过SSD 检测框架，可以返回时频瀑布图中检测出指定网台的每个跳频段的归一化坐标(y1,x1,y2,x2)。将检测出的归一化坐标按比例乘以采样频率fs就可以得到跳频信号跳变的中心频率和瞬时带宽。同理，将检测出的归一化坐标按比例乘以采样时间就可以得到每一跳的驻留时间，该过程的计算式为：

式中：f为依据归一化坐标按比例得到跳频信号跳变中心频率；y1为每个跳频段的下边界；y2为每个跳频段的上边界；fs为跳频信号的采样频率；B为依据归一化坐标按比例得到跳频信号跳变的瞬时带宽；x1为每个跳频段的左边界，x2为每个跳频段的右边界，R为每一跳的驻留时间，Ts=1/fs。

如图5 所示为在SSD 检测框架下去噪后对双网台的中一个网台的跳频信号的识别效果，图中x轴表示时间，单位为s；y轴表示频率，单位为Hz。如图6 所示为不同信噪比条件下该方法对跳频信号参数估计的精确度的统计。

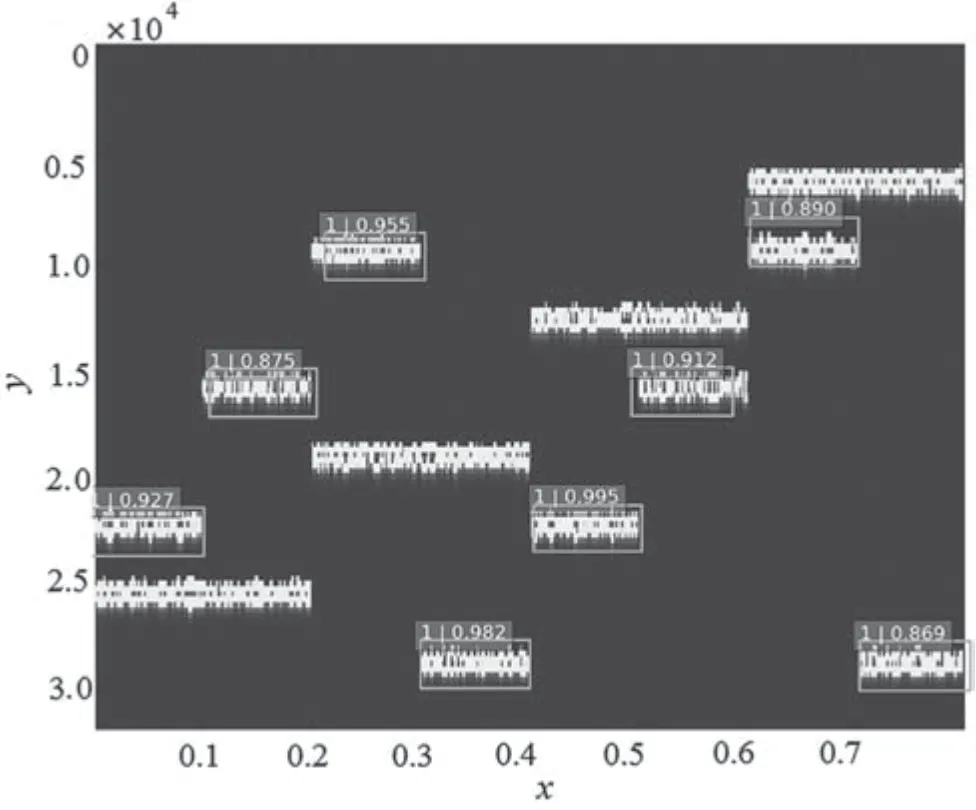
图5 去噪后对双网台中1 个网台的跳频信号时频图的参数估计

图6 去噪后对双网台中1 个网台的跳频信号时频图的参数估计精确度

3 基于图像处理的跳频信号网台分选

如图7 所示，在两个网台中分选出指定网台的跳频信号，指定只识别跳频周期较短的那段跳频信号。其中x轴表示时间，单位为s；y轴表示频率，单位为Hz。从图7（a）可以看出，在SSD 检测框架下可以识别出大部分短跳频周期的那段跳频信号，但仍然有部分识别错误，并且每段跳频信号的识别效果评分都较低。从图7（b）可以看出，在SSD 检测框架下经过自适应定门限二分聚类算法的时频图修正后，多网台的跳频信号的识别效果有了很大的提高，出错率较低，并且每段跳频信号的识别效果评分都较高。由此可以得出结论，本文方法可以用于识别和检测多网台的跳频信号，比当前主流的检测方法具有更加广泛的适用性。

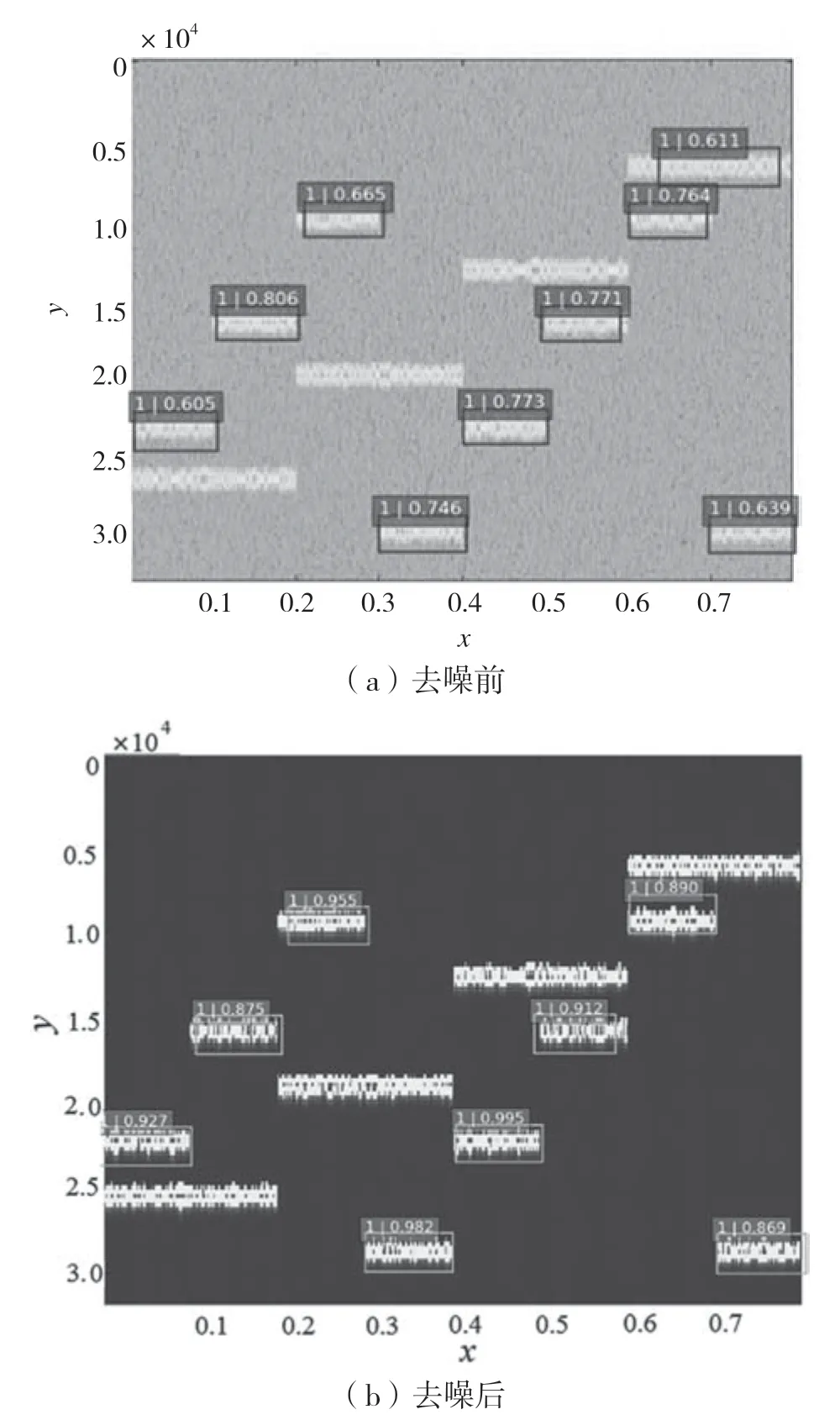
图7 双网台跳频信号中分选指定网台的跳频信号的时频图去噪前后对比

此外，从图7 中可以看出，在低信噪比下修正后的检测率对比修正前大大提高，这说明通过自适应定门限二分聚类算法来对时频图进行修正可以提高跳频信号的检测效率，且自适应定门限二分聚类算法的时频图修正步骤简洁，计算量比较小，在实际工程中可以广泛使用。

4 结语

本文针对多网台的跳频信号的参数估计和网台分选问题，提出了使用图像处理的方法。针对低信噪比的情况下识别率低的问题，提出了适用于图像处理去噪的自适应定门限二分聚类算法，该算法比当前主流的方法具有更高的识别精确率和更广的适用性。