基于改进LeNet-5 网络的数字电表识别

张宁宁,赵明冬,周 斌,马金辉

(郑州科技学院,河南 郑州 460064)

0 引言

由于在特殊场景中,人工抄表速度低下,同时会对工作人员的生命安全造成威胁,在此背景下,数字化、智能化、无人化数字仪表识别应运而生,并成为解决上述问题的重要手段。 为解决图像预处理效果不理想[1]的问题,国内外学者做了很多研究,吴响军等[2-3]提出了最小二乘支持向量机参数优化方案,后来又基于树莓派平台实现电子血压计示值和水表识别,该平台适用于电脑系统,但不满足于实际的识别需求。 为了提高图像识别精确度,陈英等[4]又提出了Enhanced Faster R-CNN 网络,但该网络仅适用于质量较好的图像,在特殊场景下仍然缺乏鲁棒性;曲超然等[5]引入注意力机制改进卷积循环神经网络算法,可实现简化运算和优化字符粘连的目标;吉训生等[6]和熊勋等[7]提出的卷积神经网络识别,对硬件资源的需求较高。 此外,王望等[8]针对双半字符识别率较低的情况,选择卷积神经网络提高双半字符的识别率和鲁棒性。

在卷积神经网络研究中,网络的性能与复杂度有关。 特殊场景应用下,过度复杂的网络损失率波动较大,硬件资源需求较高,会显著降低网络的鲁棒性。为此,本文采用ReLU 激活函数和dropout 算法相结合,缓解网络梯度消失现象;采用激活离群值去除和卷积Inception-SE 模块,提升网络训练速度;采用全局池化层,防止模型过度拟合。

1 算法分析

1.1 传统卷积神经网络模型

传统神经网络通过人工标注提取特征,卷积神经网络则通过自身网络来完成图像特征的提取,能够有效地精简工作量,提升网络总体识别速率。 首先,将电表图像做预处理操作,便于后续提取特征;然后,将所提取出的特征压缩降维并分类;最后,输出网络的识别结果。

卷积神经网络原理如图1 所示,该模型由输入层、卷积层、池化层、全连接层以及输出层组成。 输入层将识别图像进行数据标准化、归一化和中心化等预处理操作,有效加快神经网络收敛速度,缩短样本训练时间。 卷积层由多种卷积核组成,可提取多种特征,但多种卷积核易导致信息冗余。 因此,选取合适的激活函数,可增强提取特征和网络非线性运算。 池化层将卷积层提取的特征压缩并降维,能够有效降低网络参数及样本训练量,加速神经网络的运算,防止模型过度拟合,优化神经网络的稳定性,用以适应多种特殊应用场景。 全连接层将特征非线性组合,降低特征位置在分类中的影响。 输出层采用归一化进行特征分类,通过输出多个识别概率值,最终将最大概率值所对应的标签作为识别图像结果。

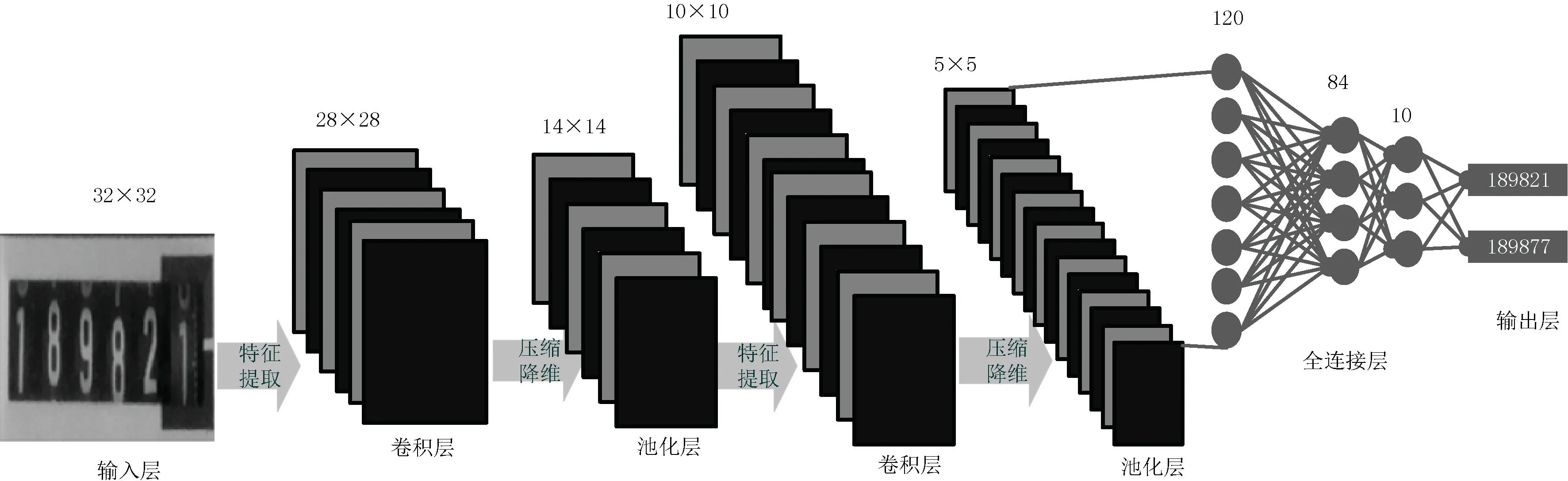
图1 卷积神经网络原理

1.2 改进LeNet-5 网络模型

1.2.1 激活离群值去除

激活离群值去除法采用较少的校准信息,获取合适的量化参数,从而提升模型量化速度。 由于激活函数对输入图像产生不同的响应,可采用阙值去除法进行动态离群值去除操作[10]。 激活离群值去除流程如图2 所示,定义离群值百分比参数α,计算离群值阙值γ。 激活离群值清除操作简单且耗时短,可视为图像预处理。 激活离群值剔除具有横跨不同网络模型的普遍适应性,有效提高量化后模型精度。

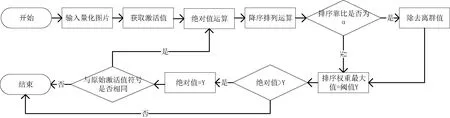
图2 激活离群值去除流程

1.2.2 Inception-SE 模块

卷积 Inception-SE 模块采用2 个3×3 的卷积核代替5×5 的卷积核[12],该模块内各层任务简单且不相同,能够有效降低网络表征学习的复杂度。Inception 模块可增强有效特征,抑制无效特征。 经改进后,网络可并行执行多个特征操作,形成较深的特征图,加深网络深度。 SE 模块降低特征维度输入,通过激活函数恢复到曾有维度,再通过全连接层,有效提高了卷积神经网络表达能力。

1.2.3 ReLU 激活函数

针对复杂的特征提取,采用合适的激活函数可有效提高网络的运算速度——ReLU 函数和Sigmoid 函数均为神经网络常采用的激活函数。 在接近饱和区时,Sigmoid 函数变化缓慢且极易造成信息损失。ReLU 函数在某些神经元之间的输出结果为0,可有效避免梯度消失,缩短运算周期,加快网络收敛速度,缓解过拟合现象。

1.2.4 全局池化层

全连接层是LeNet-5 网络中最大的网络级,由于全连接层需将卷积和池化操作后的特征进行分类操作,故运算时间最长。 参数量影响全连接层的运算时间,为了提升总体样本训练速度而降低参数量,全连接层引入了全局池化层和softmax 损失函数,将多个标量映射为一个概率分布。

1.2.5 dropout 算法

神经网络由于受噪声干扰和模型复杂度等其他因素影响,在特殊应用场景应用中泛化能力和鲁棒性较差。 选用正则化和丢弃某些无用的特征,可改善过拟合现象。 普通的正则化仅降低参数的大小,无法降低参数量。 dropout 算法可以削弱神经网络之间的相互依赖性,从而实现高效的网络模型训练[14]。 依据所设概率p 判断神经元能否被保留,丢弃部分神经元获得新的子网络模型。 例如,卷积神经网络模型中存在a 个神经元,将模型取样可得2a个子网络,将不同子网络进行迭代训练,网络最终趋于不同网络模型的平均值。

1.2.6 训练模型

本文输入分割步长为1 的28×28 数字电表图像,采用ReLu 激活函数,削弱参数之间的相互依赖性,从而缩短训练的计算时间,提高模型的收敛速度。 算法训练模型如图3 所示,经过卷积层处理后,可获得96 个28×28 图像特征。 卷积Inception-SE 模块中第三层和第五层构造相同而卷积核的数目不等,第三层共有4 个分支,卷积核个数分别是160,64,16,24,第五层的卷积核个数分别是256,176,32,24。

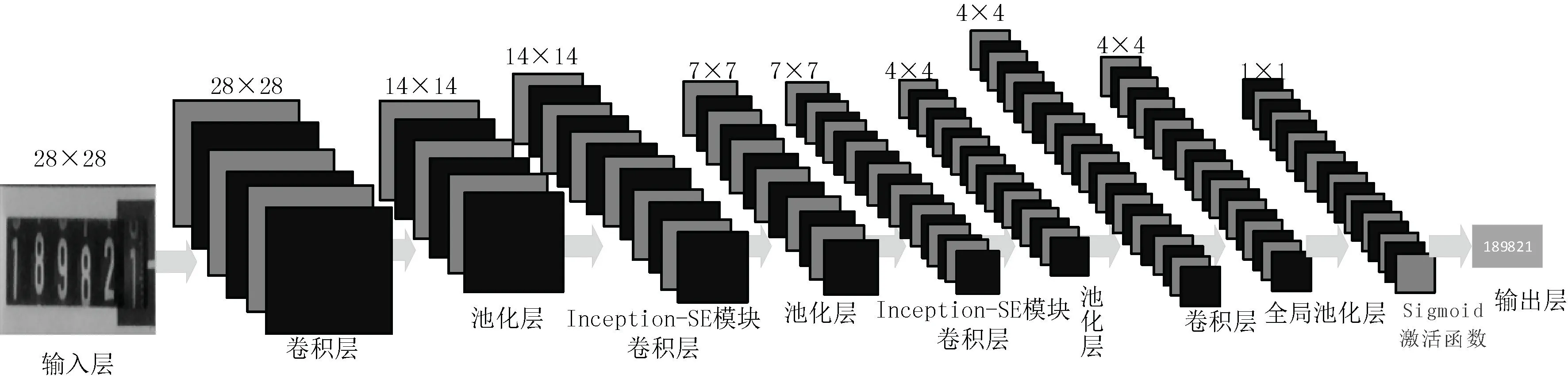
图3 改进LeNet-5 网络模型识别数字电表训练模型

2 实验与分析

本实验在Windows 10 系统Tensorflow 框架下搭建神经网络模型,处理器为i5-1235U,内存为16 GB,显卡为RTX2050。 通过将已积累的和ImageNet 数据库中电表图像进行裁剪、旋转、拉伸、缩放以及局部加厚等处理,丰富模型原始图像数据库。

2.1 网络识别率比较

设置0.1%的学习速率,调整采样数据的迭代次数以改善早期卷积神经网络的不稳定性。 通过实验验证,loss 值和网络精度对比如表1 所示,改进后网络仅需600 次迭代训练即可收敛,相较于原始网络的迭代训练减少300 次迭代训练。

2.2 最优精度Dropout 值

Dropout 值影响网络识别精度效果,Dropout rate过高或者过低极易造成识别效果不佳。 不同Dropout值的识别精度如图4 所示,当Dropout rate 为0.3%时,改进后网络识别效果最优。

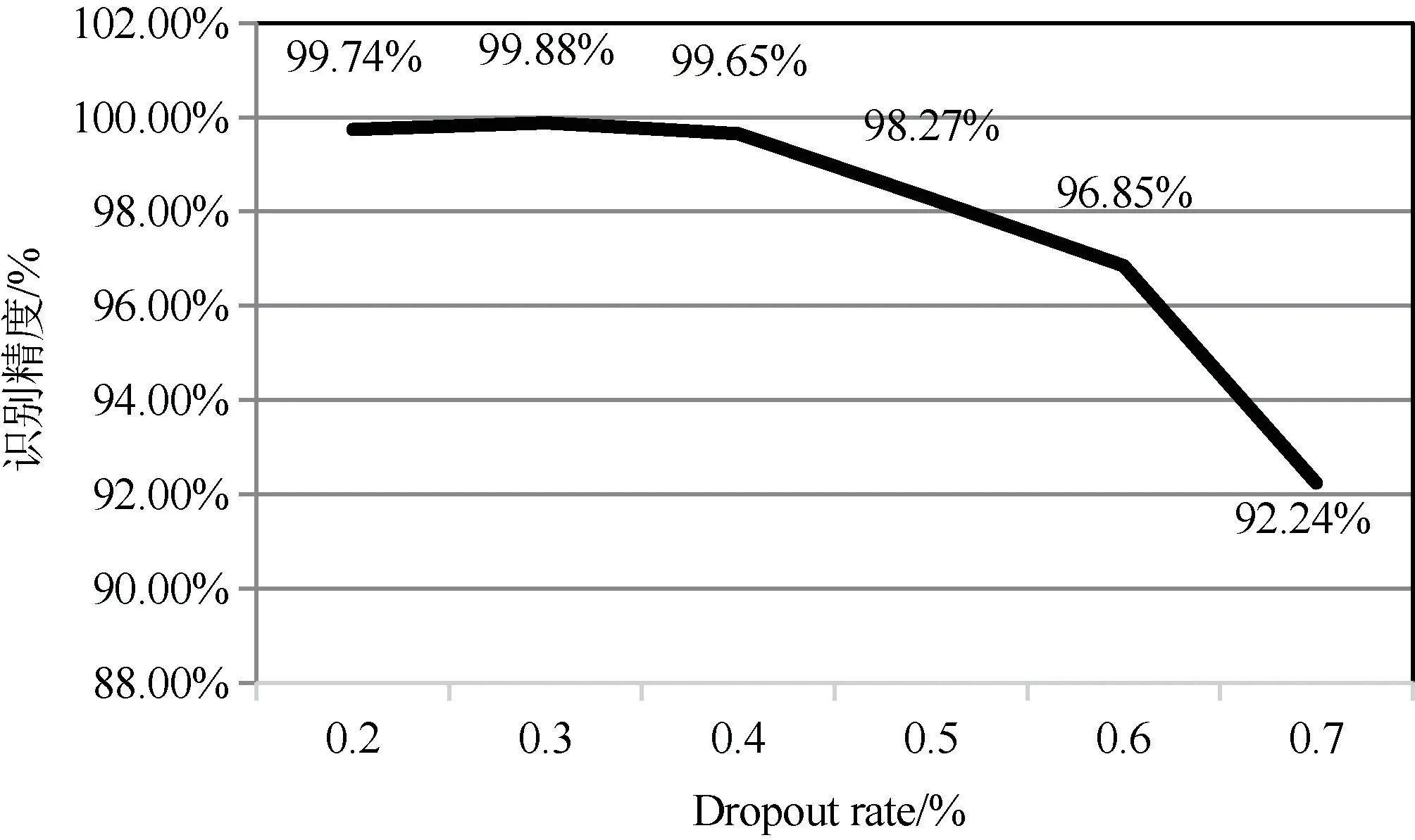
图4 不同Dropout 值的识别精度

2.3 训练时间

设定0.1%的学习速率和300 的迭代次数,在相同的特殊应用场景下分别对原网络和改进后网络模型进行训练和识别验证。 如图5 所示,在训练样本数为12 000 份时,改进后网络每份样本训练时间仅需0.09 s,相较于原网络缩短0.05 s。 实验结果表明,改进后网络模型的综合识别性能高于原网络模型且能较快、精准地收集数字电表数据。

图5 算法训练时间对比

3 结语

本文研究了卷积神经网络LeNet-5 在数字电表识别中的应用及改进方法,改进后的模型丰富了提取特征、优化了网络结构,也缓解了过拟合现象。 研究结果表明,对原LeNet-5 网络改进有效,通过改进后LeNet-5 网络模型进行测试实验,在0.1%的学习率、600 次迭代次数以及Dropout rate 为0.3%时,改进后的网络精度达到99.42%且Loss 值降低到0.11;在迭代次数为300 和训练样本数为12 000 份时,改进后网络算法训练时间仅耗时0.09 s。 本次研究不仅可快速、准确地获取数字电表数据,而且针对网络结构的改进,提出了可采用硬件采集系统提升网络的识别精度,具体有待下步深入研究。