Python 语言在数值计算中的应用

罗堂耘,陈卓鑫

(成都理工大学,四川 成都 610059)

0 引言

数值计算是强大的问题求解方法,它能处理大规模方程组,尤其是非线性系统的问题。 在工程中,用解析方法对其求解几乎是不可能的,此时计算数值解就显得尤为重要[1]。

在数值计算领域,MATLAB 是最常用的工具,而Python 语言多用于人工智能、机器学习等方面。Python 入门简单,有易学、开源等特点,更重要的是MATLAB 中大部分常用的功能都可以在Python 中找到对应的扩展库,故而Python 在数值计算领域中也颇有建树[2]。

本文利用Python 语言,对一道现实的数值计算问题作解答研究。

1 问题提出

某地有一个高40 ft、底面直径57 ft 的圆柱形水塔,每天向小镇上的居民供应生活用水。 每隔一段时间测量一次水塔中的水位,测得数据如表1 所示(两次水泵启动向水塔中加水的过程没有水位记录)。 试估计一天的总用水量。

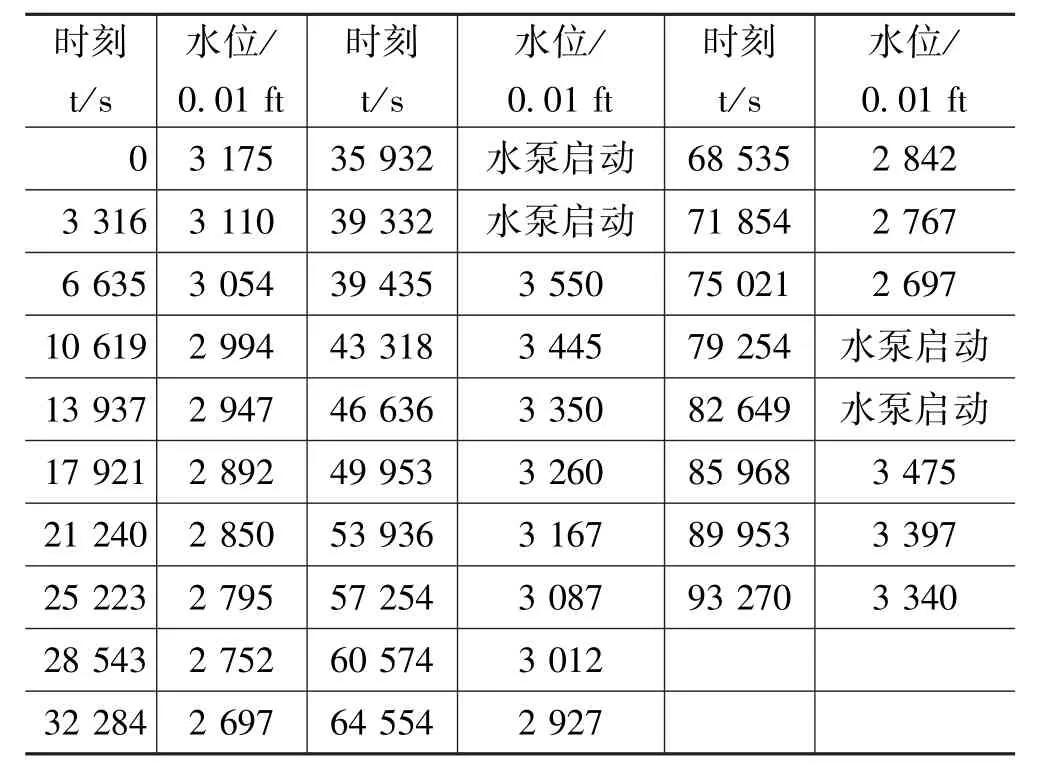
表1 某地某天水塔水位测量记录

求解该问题,首先需要建立水位对于时间的函数,随后根据离散点的公式得到各时间点的流速,再利用3 次样条插值得到流速与时间的关系,对流速函数作数值积分,进而估计出问题给定时间内的总用水量,最后得到一天的总用水量。

2 Python 扩展库

2.1 Numpy 库

Numpy 是Python 中的科学计算库,是Python 可以高效处理数组并进行矢量运算的保障。 Numpy 库使得运算效率比用户手动作数组运算要高许多[3]。

2.2 Scipy 库

Scipy 在NumPy 的基础上增加了许多科学计算、工程计算的模块,例如线性代数、微分方程和曲线拟合等[4],利用这些功能可以更高效地作数值分析。

2.3 Matplotlib 库

Matplotlib 是Python 中最著名的绘图库,可以绘制各种精美的图表、快速生成柱状图、散点图、饼状图、折线图、等值线图和三角网格等[5],配合Numpy模块使用,可以实现科学计算结果的可视化显示。

3 模型的建立与求解

为了简化模型的复杂程度,但凡是本文未提及的细节,一切都视作理想情况。 如假定水泵抽水的速度是均匀的,水流速度是连续变化的。

3.1 数值微分

除去水泵启动的4 个时刻点,还有24 个时刻点可供用于数值微分。 将水泵工作看作是每两段时间的分隔标识,即将第0 s 到第32 284 s 这段时间记为第一段,第39 435 s 到第75 021 s 这段时间记为第二段,第85 968 s 到第93 270 s 这段时间记为第三段。

利用多点数值微分公式即可算出流速,具体如下。

这不需要手动计算,以第一段为例,可以利用如下的Python 代码快速得到结果。

n1=9

for i in range(0,n1+1):

if i<=1:进行计算;

f[i] = abs((-3×v[i] + 4×v[i+1]-v[i+2])/(2×(t[i+1]-t[i])))

elif i<=n1-3:

f[i] = abs((-v[i+2]+8×v[i+1]-8×v[i-1]+v[i-2])/(12×(t[i+1]-t[i])))

elif i>=n1-2:

f[i] = abs((3×v[i]-4×v[i-1]+v[i-2])/(2×(t[i]-t[i-1])))

第二段与第三段按类似的操作进行即可。

这样便得到了24 个点,每个点在x 轴上的值对应时间,y 轴上的值对应流速。

3.2 三次样条插值

样条(Spline)一词来源于绘图技术,在绘图中常用一根窄的、柔软的条子画出一条经过一组已知点的平滑曲线,这根条子就是样条。 在所有的样条插值方法中,最常用的是三次样条插值法,将一个函数分为若干小区间,在每一个小区间上都有一个三次多项式。

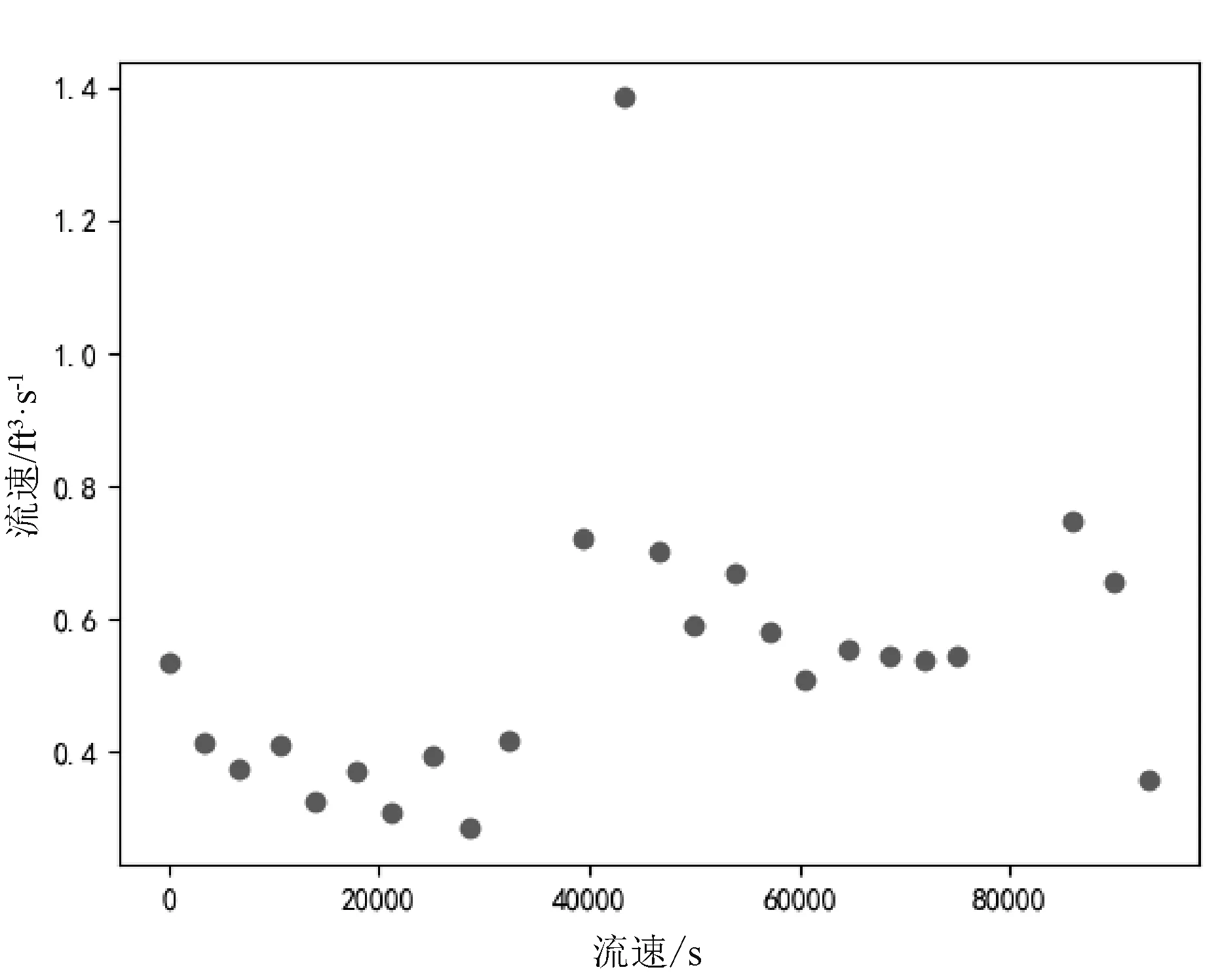
图1 流速-时间图像

前面已经得到了24 个点的水流速f(t)的值,故只需根据这24 个值作三次样条插值即可。 三次样条插值的基本思想如下[6]。

(1) 输入节点个数n,节点x0,x1,x2…xn,对应函数值y0,y1,y2…yn。

(2) 计算步长hi及差商f[xi-1,xi],i = 0,1,2…n。

hi= xi- xi-1

(3) 计算参数λi,μi,di,i=0,1,2…n。

μi= 1 - λi

di= 6f[xi-1,xi,xi+1]

(4) 得到各参数后,可将待解式写作如下的矩阵形式。

(5) 解上式得到:M0,M1,M2…Mn-1。

通过手动计算或编程来实现三次样条插值十分复杂烦琐,可以借助Python 中的Scipy 库为接下来的数值计算研究节省时间。 利用如下的Python 代码即可求解。

tck=interpolate.splrep(x,f)

xx=np.linspace(min(x),max(x),360)

yy=interpolate.splev(xx,tck,der=0)

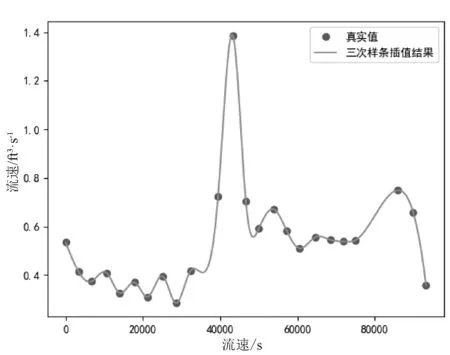
图2 三次样条插值结果

3.3 数值积分

正如人们所熟知的牛顿-莱布尼茨公式,若F(x)是f(x)的原函数,则有积分式I=∫baf(x)dx=F(b)-F(a)。

但实际上这是有困难的,如本问题:计算流速f(x) 的原函数F(x) 很困难,甚至是无法实现的。 数值积分方法由此被提出。

3.3.1 整体积分

在得到f(x)之后,再对其整体进行一次数值积分——以0 为积分下限,96 270 为积分上限,180 为步长。 这样便得到了测量时间内的总水流量,进而也就可以得到一天(86 400 s)内水的总流量。

复合梯形公式是常用的数值积分方法,为:

利用如下的Python 代码进行计算。

tck=interpolate.splrep(x,f)

t2=np.linspace(start = 0, stop = 96 270, num =510)

nn=len(t2)

f2=interpolate.splev(t2,tck,der=0)dt=180

s=(f2[0]+f2[nn-1]+2×sum(f2[np. arange(1,nn-2)]))×dt/(2×3 600)

最终得到测量时间内水的总流量为49 155.641 6 ft3,进而得到一天时间内水的总流量为44 586.333 0 ft3。

3.3.2 分段积分

鉴于水塔水泵一共工作了两次,故可使用数值积分分别计算3 段时间内的流量,再将各段流量相加得到总流量。 换言之,就是将原本的一次整体数值积分改成了3 次分段数值积分,并将各段结果相加。 此操作细节与整体积分类似,不再赘述。

计算得到:测量时间内水的总流量为 48 121.033 9 ft3,进而一天内水的总流量为43 647.898 3 ft3。

4 结语

本文讨论了使用Python 进行数值计算的优势和应用。 Python 语言语法简单,其可读性和可维护性使其成为一种理想的工具,且配备有极其强大的第三方库,可以满足各种数值计算需求。 本文以一道现实生活问题为背景,介绍了诸多数值计算领域中的经典方法,使用Python 语言将这些方法依次实现,并串联起来,希望能为读者在相关问题上的研究提供一定的参考及帮助。