基于强化学习的跳频抗干扰系统设计

邹雯雯

(河南农业大学 机电工程学院,河南 郑州 450003)

0 引言

在移动互联网时代,无线通信成为日常工作和学习的重要工具。 但信号在传输过程中有可能被窃听、截获,甚至受到人为攻击。 干扰机可向信号接收方发送干扰信号,进而引起较高的误码率,降低通信质量和用户体验。 传统的跳频抗干扰系统面临较为严峻的技术挑战,其主要问题在于缺乏主动规避干扰信号的能力,因此优化跳频抗干扰系统的算法成为解决问题的关键。

1 跳频抗干扰系统的应用场景、通信模式及缺点

1.1 跳频抗干扰系统的应用场景

跳频抗干扰通信系统的应用场景可简化为如图1 所示,正常情况下由发射机向接收机发送无线通信信号,但干扰机也能接收同类信号,同时向接收方发送干扰信号,接收机获取信号后需进行解码处理,干扰信号会导致其误码率上升。 此处的干扰机用于代表各类人工干扰方式,如主动攻击、窃听等。

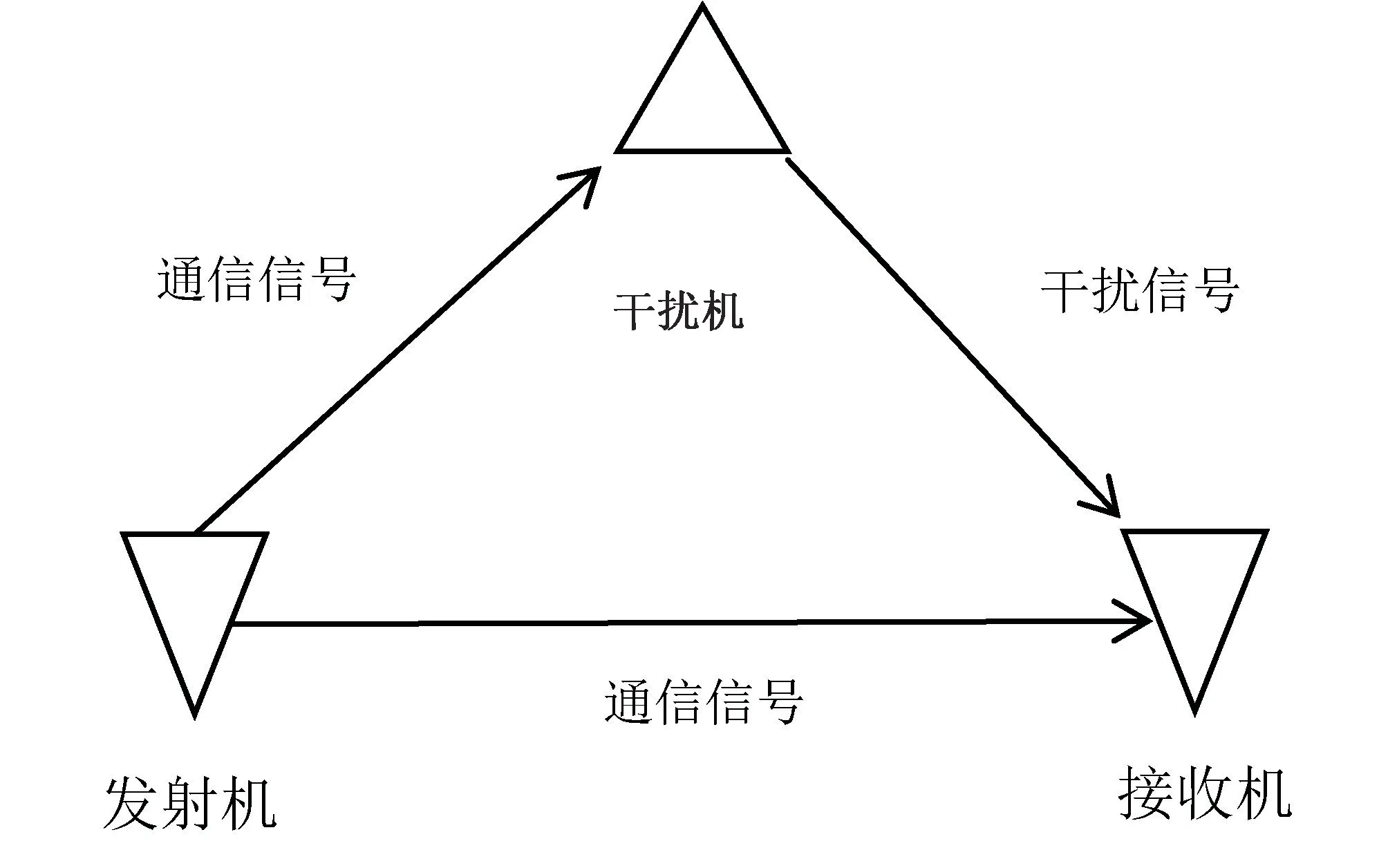
图1 跳频抗干扰系统的通信应用场景

1.2 跳频抗干扰系统的通信模式及缺点

1.2.1 通信模式

跳频通信是指发射方和接收方按照相同的频点序列发送和接收信息,频点之间呈正交关系。 进入通信模式后,双方必须同时选择同一个频点,经过时间τ 后,跳转至另一个频点(也可以继续在原频点通信)。 跳频技术的应用显著地提高了通信抗干扰能力,但这种通信技术不能完全避免外部干扰,仍然有部分干扰方式能够对其发挥作用。

1.2.2 缺点分析

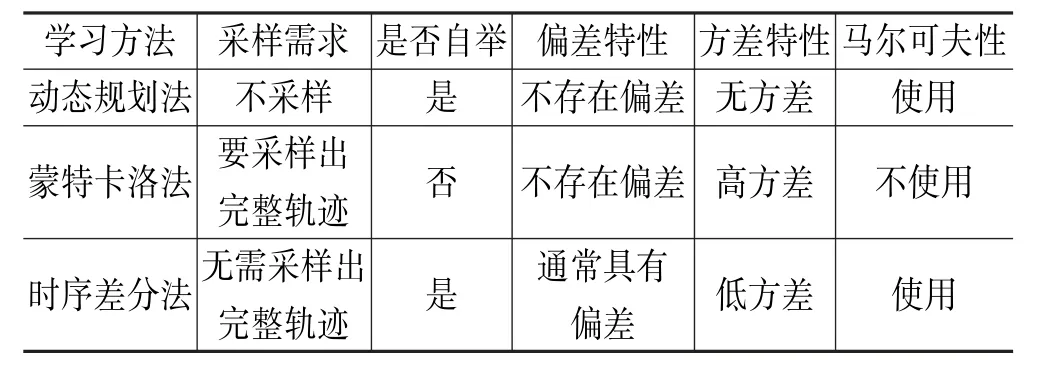
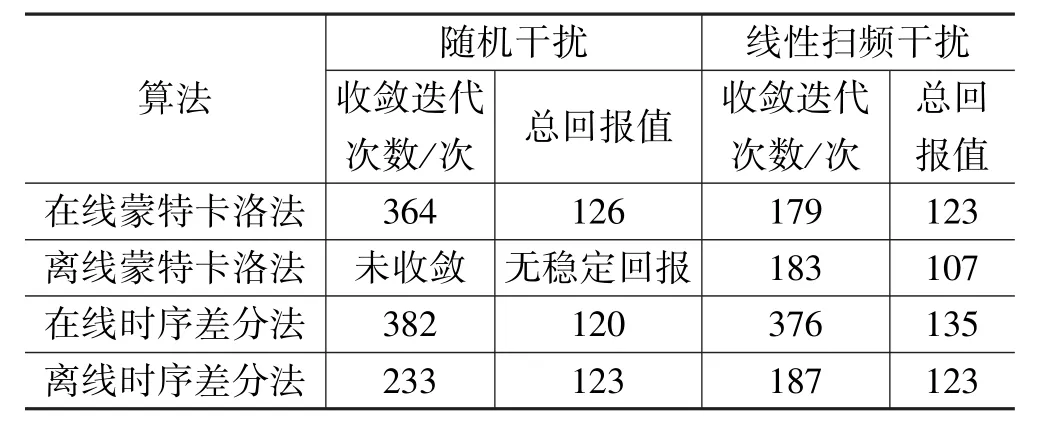
假设发射机和接收机在K 个频点上进行跳频通信,将频点编号为0,1,2…(K-1)。 线性扫频干扰方式能够在0~(K-1)随机选择一个频点实施干扰,每经过时长τ 后,增加一个新的干扰频点,扩大干扰范围,这一过程称为线性扫频。 随机周期干扰也能影响跳频通信技术的性能,这种干扰方式在K 个频点范围内随机选择G 个频点(G

2 基于强化学习的跳频抗干扰系统优化设计方法

2.1 强化学习的理论基础

2.1.1 基于马尔可夫性的强化学习模型基础

马尔可夫性在概率论中具有重要的应用,其含义为一个随机过程在未来状态的概率分布情况仅取决于当前状态,随机过程中已经产生的历史状态不影响未来的概率分布。 基于强化学习的跳频抗干扰系统符合这一特点,将跳频抗干扰模型的通信状态表示为si,j,其中i 表示发射机和接收机的通信时隙,j 表示通信时的频点,此时马尔可夫性可表示为:

式中,St=si,j。 从表达式可知,概率分布P 与通信状态St和St+1有关。

研究中提出的跳频抗干扰模型基于马尔可夫性原理进行通信决策,其中包括5 个参量,可记为M=R,A,P,S,γ,参量的含义按照M 中的顺序分别为收益函数、选择下一个通信频点的决策行为、通信频点发生迁移的概率、当前的通信状态信息、衰减系数[2]。

2.1.2 强化学习的实现机制

强化学习的根本目标是解决传统跳频抗干扰通信模式缺乏干扰识别能力和应变能力的问题,因此其实现机制的核心工作是形成具有识别能力的跳频通信决策(记为π),以当前的通信状态s 为根据,在决策π 的作用下,产生通信决策行为a,这一过程可表示如下:

式中,s 和a 分别表示S 和A 在时刻t 的取值。显然,a 和s 能够显著地影响决策π,可通过状态值函数Vπ(S)和行为值函数Qπ(s,a)迭代计算π,s,a 之间的关系。

2.2 蒙特卡洛法优化跳频抗干扰系统

蒙特卡洛法利用统计学原理模拟复杂问题,其特点为通过反复抽样,逐渐逼近实际情况,反映客观规律。 该方法能够提高跳频抗干扰系统通信模型的精确度,在具体实施过程中对历史通信数据进行采样,再实施统计学模拟,最终形成通信轨迹,该轨迹反映了信息发射方、接收方在各个通信时隙的决策动作。蒙特卡洛法的实施不依赖通信模型,而是利用贝尔曼期望方程进行模拟和近似,进而实现通信决策的收益最大化。

2.2.1 蒙特卡洛法优化跳频抗干扰系统的基本原理

当跳频抗干扰系统采取决策π 时,当前时刻t 的状态为s,将对应的期望回报记为Gt,状态值函数Vπ(S)可描述这一过程。 同样的,在决策π 背景下,行为值函数Qπ(s,a)表示状态s 对应决策行为a 的期望回报。

式中,Gt表示期望回报。 蒙特卡洛法的主要作用是代替以上两个函数中的期望计算过程,以大量的统计学模拟获得各个通信状态的平均值,形成多种通信轨迹。 在蒙特卡洛法的支持下,每个状态对应的行为值函数均可计算出具体的结果,通过对比即可确定最优的通信策略。 为了达到全局层面的最优决策,就要使用强化学习,探索各种通信状态。 此时,经过蒙特卡洛法优化的跳频抗干扰决策可表示为:

式中,M 表示决策动作的数量,ε 代表选择某个决策动作的概率。

2.2.2 基于蒙特卡洛法的两种强化学习模型

基于蒙特卡洛法的强化学习对数据提出了较高的要求,根据数据的来源,可将强化学习分为在线和离线两种模式。

(1)在线蒙特卡洛强化学习。

在线强化学习中,将干扰信号表示为时频矩阵,记为J,以便开展数学运算;将通信状态表示为集合S,决策动作形成的空间记为A。 对行为值函数和策略π 进行初始化,利用蒙特卡洛法实施迭代运算,策略π 每做出一次跳频选择,即可得到一个确定的决策动作,记为ai,所有动作形成决策轨迹T,则有T={a1,a2…aT}。在过程中对每个时隙τt对应的收益Gt、行为值函数Q(s,a)以及决策π进行同步更新,最终得到最优决策π∗[3]。 在这种学习模式下,决策π负责在线数据采集,因而数据采集策略也同步得到更新。

(2)离线蒙特卡洛强化学习。

离线蒙特卡洛法的实施过程与在线法基本一致,主要区别为数据采集策略与算法中优化的决策π 不同。 这种学习模型为数据采集设计了专门的行为策略,而蒙特卡洛法持续优化的策略称为原始策略,两种策略可分别记为π 和π′。 相比于在线蒙特卡洛法,离线方式存在一定的性能优势,降低了策略选择的随机性,其每次优化的决策π′都是对应状态的最优策略。

2.3 时序差分法优化跳频抗干扰系统

2.3.1 不同强化学习方式的对比

为了获得最佳的强化学习方法,研究中需对比不同学习路径的优劣性。 除了利用蒙特卡洛法开展强化学习外,还可使用动态规划法和时序差分法。 表1总结了3 种学习方法的特点,既有共性,也有差异,其根本原因在于3 种方法的值函数计算方式不同。 蒙特卡洛法在值函数原始定义的基础上,通过大量的采样和模拟进行更新,且只有采样获得完整的轨迹后才能更新。 动态规划法和时序差分法在更新方式上类似,都采用了自举。 另外,3 种学习算法对马尔可夫性的适用性有所差异,蒙特卡洛法可用于处理无马尔科夫特性的问题,另外两种算法则适用于存在马尔科夫特性的问题[4]。

表1 3 种强化学习算法的特点

2.3.2 基于在线时序差分法的强化学习

假设跳频抗干扰系统当前的状态为S,按照策略π 做出选择,产生行为A,同时得到了状态行为值Q(S,A)和收益R。 完成第一次选择后状态发生了变化,将新的状态记为S′,继续进行决策,于是产生了与S′对应的A′,R′及Q(S′,A′)。 基于在线时序差分法的强化学习能够以较高的频率更新策略,达到收敛的耗时比蒙特卡洛法更短。 该方法的优化路径如下[5],在算法中输入干扰时频矩阵J、动作空间A 以及状态集合S,对行为值函数Q(S,A)和原始策略π 进行初始化,利用在线时序差分法开展迭代计算,在策略π的作用下产生第一个动作a,形成行为状态对(s,a),持续按照这一模式进行更新迭代,产生最优策略π∗。

2.3.3 基于离线时序差分化的强化学习

离线时序差分法的实施步骤与在线时序差分法基本相同,区别在于状态行为值函数的更新公式,Qlearning 算法可用于离线时序差分中的Q(st,at) 更新,该算法的公式如下:

式中,a′表示时刻t+1 时选择的行为,其对应的策略为π′。

2.4 仿真模拟

利用MATLAB 软件模拟上文设计的强化学习算法模型,对跳频抗干扰系统分别实施随机干扰和线性扫频干扰,如表2 所示为仿真模拟的数据。 在随机干扰模式下,基于离线蒙特卡洛法的强化学习算法未能完成收敛,另外3 种学习算法均能完成收敛,在线蒙特卡洛法的收益最高,但3 种可收敛算法的收益较为接近,离线时序差分法达到收敛所需的迭代次数最少,明显优于在线时序差分法和在线蒙特卡洛法,说明其在实际应用中具有更高的运行效率,有利于提高通信速度。 在线性扫频干扰模式下,4 种算法都能实现收敛,从最佳收益来看,在线时序差分法效果最佳,但达到收敛所需的迭代次数也最高,剩余3 种算法的迭代次数较为接近,都在180 次左右。

表2 算法仿真结果

为了提高算法模拟的可靠性,多次开展试验,将总迭代次数提升至8 万次。 在随机干扰模式下,离线时序差分法的平均收敛迭代次数为98 次,离线蒙特卡洛法为209 次,在线蒙特卡洛法为402 次,反映出离线时序差分法的效率优势。 在线性扫描模式下,同样开展多次仿真试验,总迭代次数达到8 万次,计算每种强化学习算法达到收敛的平均迭代次数,收敛最快的为离线蒙特卡洛法,迭代次数为204 次,剩余3 种算法的收敛迭代次数在400 次左右。 总体而言,利用蒙特卡洛法和时序拆分法能够提升跳频抗干扰系统的性能,使其能够主动规避随机干扰和线性扫描干扰。

3 结语

在跳频抗干扰系统中引入强化学习算法的目的是提高其对部分干扰信号的识别和规避能力,防范重点为随机干扰、线性扫描干扰。 研究过程以蒙特卡洛法和时序差分法为基础,分别构建在线蒙特卡洛强化学习算法、离线蒙特卡洛强化算法、在线时序差分强化学习算法以及离线时序差分强化学习算法。 对比分析4 种算法的特点,通过MATLAB 仿真试验对其抗干扰性能进行检验。 结果显示,在线性扫频干扰模式下,算法均能完成收敛,在线时序差分法性能表现最佳。 在随机干扰模式下,只有离线蒙特卡洛法未完成收敛,其余算法在性能上基本一致。 下一步需提高仿真检验的规模,取多次试验的平均值,观察算法性能表现上的差异性。