面向特征演变环境的标记噪声鲁棒学习算法

张震宇 姜 远

（南京大学计算机科学与技术系 南京 210023）（zhangzy@lamda.nju.edu.cn）

传统的机器学习任务通常假设学习环境稳定不变，并且收集的数据标记是高质量的.然而，在实际的应用场景中，数据在开放变化的环境中不断累积，而且数据标记往往是带有噪声的.具体而言，随着学习环境的变化，数据的特征空间可能发生演变.与此同时，数据的标记可能不准确.这类问题在现实应用中广泛存在，并且具有重要意义.以环境监测任务为例，研究者在野外部署传感器以监测种群信息.传感器不断收集数据，每个传感器收集的数值对应着一个特征，所有传感器收集的数据组合在一起形成了数据的特征空间.由于传感器使用寿命有限，因此研究人员需要用新的传感器替换损坏的传感器.随着时间的推移，新的特征（新传感器）出现，旧的特征（到达使用寿命的传感器）消失，学习要素发生了变化，即数据的特征空间发生了演变.与此同时，由于对数据样本的人工标注可能存在误差，数据标记可能存在噪声.因此使得学习系统具备应对开放环境下特征空间演变和数据标记带噪的能力变得至关重要[1-2].

随着数据特征空间的不断演变，学习模型需要具备处理新特征空间数据的能力，以建立具有泛化能力的学习模型.为此，建立新旧特征空间之间的关系，有效利用旧特征空间的历史数据是至关重要的.以往的研究通常考虑特征演变环境中的数据流存在特征演变阶段[3-4].研究者们通过该阶段的数据建立新旧特征空间之间的联系，从而利用历史数据帮助学习新特征空间下的分类器.以环境监测为例，如图1所示，在传感器到达使用寿命之前，研究者可以提前部署一批新的传感器用以替代即将失效的传感器.在此阶段，新旧传感器同时收集数据，因此此时的数据具有新旧特征空间的表示，形成了数据演变阶段.为了构建新特征空间上的分类器，研究者们提出了一种基于映射函数的解决思路[3].该方法利用演变阶段的数据学习映射函数，在新特征空间上学习分类器的同时，将数据映射回旧特征空间，并复用旧特征空间的模型，辅助构建新特征空间上的分类器.

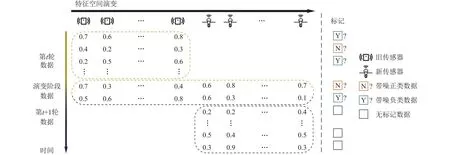
Fig.1 Learning with noisy labeled data in environments with evolving features图1 特征演变环境下的标记带噪数据学习

除了数据特征空间的演变外，由于标注过程中可能存在人为误差，数据的标记往往受到噪声的干扰[5-6].以野生动物种群监测为例，某些动物可能难以进行准确区分，如猎豹和美洲虎、狼和土狼等[7].当数据特征空间发生演变并且数据标记存在噪声时，仅仅叠加处理特征演变的算法和处理标记噪声的算法无法很好地解决这一问题，尤其是很难获得在理论上具有良好泛化性能保障的分类器.具体而言，为了应对这一难题，一种可行的方案是利用演变阶段的数据，首先学习新旧特征空间数据表示之间的映射方式，建立它们之间的联系.其次，模型可以通过旧特征空间的带噪标记数据进行鲁棒学习，得到分类器.最后，基于学习得到的映射函数，算法将新特征空间的数据映射到旧特征空间上进行预测.然而，由于演变阶段的数据较少，通过演变阶段数据学习得到的映射函数通常无法完美地还原新特征空间数据在旧特征空间上的表示，因此这种方法的效果会受到映射函数学习质量的制约.在对经过映射函数恢复出的特征表示进行预测时，算法会放大构建映射函数时所引入的误差，导致分类器性能下降.另外，通过映射函数进行学习的启发式算法缺乏理论理解，难以获得具有泛化性能保障的分类器.对于特征空间演变环境下的标记带噪数据流学习而言，目前还缺乏能够提供泛化性能保障的算法设计.因此，设计一种有效的算法，能够同时处理特征空间的演变和数据标记上的噪声，并在新特征空间上获得具备泛化性能保障的分类器，成为了当前重要的研究课题.

本文首先形式化了一种特征演变环境下的标记带噪数据学习问题.具体来说，本文考虑训练数据以流的形式不断累积的学习场景，数据特征空间发生演变，同时环境返回的数据标记存在噪声.在这种情况下，学习者需要不断对新到达的无标记数据进行预测，并期望在新特征空间上获得具有泛化能力的分类器.该问题在现实应用中经常遇到，但却没有得到深入的研究.针对这类问题，设计具有泛化性能保障的分类器十分重要且具有挑战性.为了应对这个问题，本文旨在提出一种基于数据差异最小化技术[8-10]的算法来刻画分类器在新特征空间上的泛化能力.然而，现有的数据差异最小化技术通常只考虑特征空间不变的数据，并且认为数据的标记是准确的，这在本文考虑的学习问题中并不适用.因此，为了学习具有泛化能力的分类器，学习者需要刻画特征空间演变环境下不同特征空间数据的差异度量，并设计相应的具有理论保障的学习算法.本文在数据标记存在噪声的情况下，利用演变阶段数据，建立了新旧特征空间之间的数据差异度量.基于所提出的容忍标记噪声的数据差异度量，本文进一步导出了相应的泛化误差分析结果，并提出了一种基于深度神经网络的学习算法LREDM（label-noise robust evolving discrepancy minimization）.

本文的主要贡献包括3个方面：

1） 引入并形式化了特征演变环境下标记带噪数据的学习问题，尽管这类问题在现实应用中广泛存在，但却缺乏深入的研究；

2） 定义了容忍标记噪声的数据差异度量，并基于此进行了模型泛化性能的分析，给出了模型泛化误差界的理论保障；

3） 基于提出的理论设计了相应的基于深度神经网络实现的学习算法LREDM，并且在现实应用的数据集上验证了所提算法的有效性.

1 相关工作

本文旨在研究特征演变环境下的弱监督学习.在实际应用场景中，训练数据通常来自于开放且带噪的环境，因此，学习系统具备适应学习要素变化和标记带噪数据的能力是至关重要的[1-2]，这也是稳健机器学习[11]和学件[12]的关键要求.本文主要关注2个方面：一是特征演变数据学习，二是标记带噪数据学习.接下来，本节将从这2个方面概述本文的相关工作.

1.1 特征演变数据学习

早期的工作主要研究增量属性学习[12]和梯形数据学习[13].这些研究考虑数据样本及其特征维度不断增加的情况，学习者需要不断更新模型以应对新增的数据特征.文献[14]提出了OLSF（online learning with streaming features）算法，以解决数量与特征维度随时间增加的梯形数据问题.当新特征维度到达时，OLSF算法对不同特征空间执行不同的在线更新规则，使分类器不断适应新特征维度.与这些研究不同的是，本文的研究问题考虑在新特征出现的同时旧特征可能消失，这为特征空间演变环境下的机器学习带来了新的挑战.为了处理特征空间演变的数据流，一系列前沿的研究工作考虑建立新旧特征空间的联系，进而复用历史信息辅助对新特征空间数据进行预测和学习.文献[3]的开创性工作考虑了数据演变阶段，其中新旧特征空间的数据同时存在.文献[3]提出了FESL（feature evolvable streaming learning）算法，通过演变阶段学习映射函数，恢复新特征空间上的数据在旧特征空间上的表示.FESL算法在新旧特征空间上构建了2个学习模型，通过在线集成的方式进行预测和学习.后续的工作对演变阶段映射方法的学习进行了拓展和探索[15].文献[4]进一步研究了这一问题，建立了新旧特征空间之间的演变差异，提出了EDM（evolving discrepancy minimization）算法，最小化了分类器在新特征空间数据上的泛化误差.文献[16]则考虑了特征继承性增减环境下的学习问题.其中，新特征空间与旧特征空间的数据存在若干重叠特征，即部分特征表示在旧特征空间和新特征空间内同时存在.文献[16]提出的OPID（onepass incremental and decremental learning）算法，通过将新特征空间数据映射回旧特征空间，使得旧特征空间数据得以复用进行学习.OFID（online classification algorithm with feature inheritably increasing and decreasing）算法在此基础上对特征继承性增减环境进行了深入研究[17].此外，一些研究者考虑了数据流中特征任意增减的情况.例如，文献[18]提出的OCDS（online learning from capricious data streams）算法和文献[19]提出的OLVF（online learning from varying features）算法，将数据映射到共享的特征空间中进行统一学习.除此以外，特征演变环境下的在线度量学习[20]、演变数据特征缺失学习[21]同样得到了研究者关注.然而，大多数特征演变数据学习算法假设数据的标记是准确的，因此难以适应弱监督学习场景，尤其是当数据标记存在噪声时.

1.2 标记带噪数据学习

标记带噪数据学习旨在利用标记带噪数据训练出潜在无噪声数据分布上具有良好泛化能力的分类器.自文献[22-23]的开创性研究，机器学习领域对标记带噪数据学习进行了深入广泛地研究.本文着重研究类别相关的标记噪声，即噪声标记的形成机制仅与其真实所属类别有关.

文献[6]的研究表明，当噪声率已知时，通过设置适当的凸代理损失函数，可以在标记噪声类别下进行经验风险最小化，从而得到与无噪声数据分布上最优分类器一致的分类器.文献[24]通过代理损失分解的方法，提出了样本标记中心平滑的方法，降低了标记噪声的负面影响.然而，在实际应用中，学习问题往往面对噪声率未知的场景.此时，估计噪声率或噪声转移矩阵是处理类别相关的均匀标记噪声的核心挑战之一.研究者们提出了一系列假设来估计噪声转移矩阵，例如锚词条件[25]、锚点[26-27]和不可约性[28-29].具体而言，文献[26]的研究考虑了噪声率未知的情况，通过估计噪声率上界的形式，给出了设计凸代理损失函数的方案，并在实验中验证了其有效性.文献[27]假设存在一些经过验证的准确数据，通过准确标记与无标记数据提取信息来估计噪声率.文献[28]对标记带噪数据做出不可约假设，即存在一些锚点.因此，学习者通过锚点从有噪声的标记数据中区分并恢复无噪声分布.通过对数据分布做出一定假设，学习者从数据中估计噪声率或噪声转移矩阵，进而恢复潜在无噪声数据分布，从而获得具有泛化性能的学习器.然而，大多数标记带噪数据学习方法集中在静态稳定环境中，一旦学习要素发生变化，例如特征空间的改变，导致这些方法往往无法直接适用.

2 预备知识

本节首先介绍特征演变环境下标记带噪数据学习的场景以及本文用到的符号和相关定义，然后对数据分布差异度量的基本概念及其应用进行回顾.

2.1 问题设定和相关符号

本节考虑特征空间演变环境中的标记带噪数据学习任务.首先介绍该场景下的数据特点，接着给出相关符号和定义，最后给出问题的形式化.

与文献[3]的先驱性工作相似，本文假设数据在特征空间演变的过程中存在数据演变阶段.如图1所示，学习者在旧传感器即将到达使用寿命之前可以提前部署一批新的传感器，防止发生旧传感器失灵后无法收集数据的问题.因此，在提前布置好新的传感器之后，学习者可以收到少量具有新旧2个特征空间表示的数据连接先后2批相邻但不同特征空间的数据块.与此同时，由于数据在收集过程中往往存在着噪声，数据的标记可能是错误的.

本文将上述场景形式化为在特征空间演变场景中的标记带噪数据的学习问题.令Xt⊆Rdt表示第t轮数据的特征空间，学习者每轮首先收到样本集合，其中∈Xt.本文考虑特征空间发生演变，因此有dt≠dt+1,t=1,2,…,T.依照传统在线学习的设置，算法首先需要对样本进行预测，随后环境返回样本的带噪标记.考虑本文的问题场景，研究二分类学习问题，即样本的类别空间Y={-1,+1}，但是观测到的样本标记存在标记噪声.对每个样本xi，本文将样本未被观测到的真实标记为yi，被观测到的噪声标记为.对于每个真实标记为yi的样本，它以一定概率以噪声标记被 观测到，这一概率根据噪声率ρ±1定义[6]，具体而言

值得注意的是，噪声率ρ±1对于算法而言是未知的.

在对t+1轮的数据进行预测时，算法具有第t轮的标记带噪数据和第t+1轮的待预测无标记数据.因此，根据本文研究场景中的数据特点，每一时刻学习者拥有的数据可以被划分成3个部分：噪声标记数据、演变阶段数据、待预测数据：

1）来自第t轮特征空间的噪声标记数据集合，记作

2） 演变阶段数据具有新旧2个特征空间Xt和Xt+1上的表示.令表示基于旧特征空间表示的演变阶段数据，表示基于新特征空间表示的演变阶段数据，其中，.

3） 来自第t+1轮的新特征空间的待预测数据，记作

值得注意的是，演变阶段并不会延续太久，因此有k≪nt和k≪nt+1.以环境监测任务为例，提前部署新传感器以替换旧传感器的过程形成了数据演变阶段，这一阶段的数据数量通常少于旧特征空间的数据.由于演变阶段样本较少，如果直接利用演变阶段数据的新特征空间上的表示进行学习，分类器会产生严重的过拟合现象.为了缓解t+1轮新特征空间上样本数量较少的问题，本文考虑利用第t轮旧特征空间的标记带噪样本辅助进行学习.表1总结了本文中使用到的主要符号及其定义.

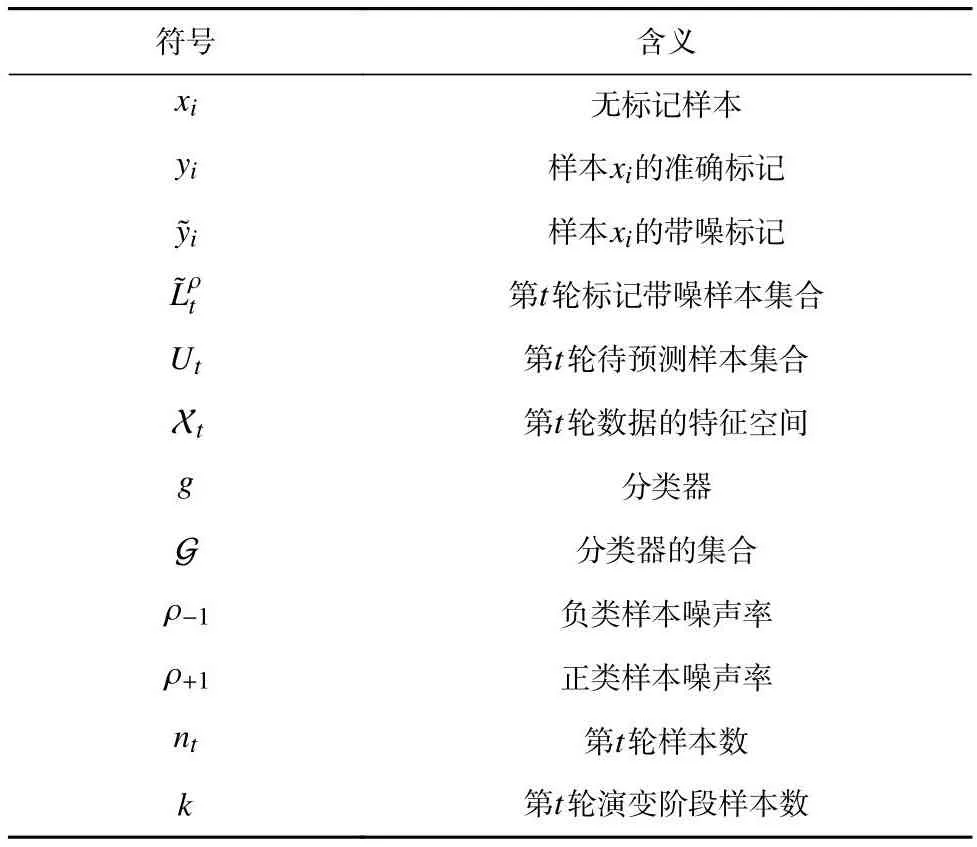
Table 1 Notations and Their Meaning表1 符号和对应含义

对于特征空间演变的标记带噪数据的学习问题，本文的目标是构建一个在新特征空间上具有泛化能力的分类器.令分类器属于给定函数族G，其中每个函数gt:Xt-→R.考虑损失函数ℓ:R×Y-→R+和函数g∈G，本文将RD(g)记作分类器的期望风险，记作分类器的经验风险，

因此，本文的学习目标是对于每一轮收集得到的样本，构建在新特征空间上具有泛化性能的分类器，即在新特征空间上获得一个期望风险较小的分类器.

2.2 数据分布差异度量

为了应对特征空间的演变，本文将借助差异最小化技术设计算法.本节回顾这一领域的相关研究内容.对于2个来自不同分布的数据集，研究者们提出了多种差异度量方式，用以刻画它们之间的差异.基于所提的差异度量，研究者们设计对应算法，将数据差异最小化，进而可以在源数据（source data）上学习分类器，并部署到另一个目标分布（target distribution）对应的数据上.例如，利用KL散度刻画分布差异的学习方法KLIEP（Kullback-Leibler importance estimation procedure）算法[30]，利用最大均值差异度量分布差异的学习方法KMM（kernel mean matching）算法[31]等.文献[8]基于所提的HΔH散度给出了一种广义的差异最小化算法的分析.后续由文献[9]拓展到了任意损失函数上.文献[32]进一步定义了Y散度，并基于此给出了更紧的泛化误差界.这些基于差异的泛化误差界启发了差异最小化算法[10].

对于训练数据集和测试数据集分布不同的问题，学习者希望利用有标记的训练数据集训练在无标记的测试数据集上具有良好泛化能力的模型.假设训练数据与测试数据属于同一个特征空间，对于一个固定的分类器g∈G 而言，它在2个不同分布P和Q上进行迁移部署的质量可以通过分类器期望损失的差异来度量.一个直观的差异度量方式就是可以通过对未知的分类器和目标函数的差异取最大值，定义为：

其中RP(·;g′)表示分类器在数据分布P上目标函数为g′的期望损失.

更进一步地，研究者们常会用Y散度[32]来衡量数据分布之间的差异最大值，其定义为：

这一定义依赖于已知的目标函数fP和fQ，它们是分布差异disc(P,Q)的一种推广.

值得注意的是，这些方法通常假设数据分布在同一个特征空间内，因此不适用于本文考虑的特征空间发生演变的学习场景.

3 理论与方法

本节为特征空间演变环境下的标记带噪数据学习问题建立理论与方法.为了获得具有泛化性能保障的分类器，首先重写了分类器在新特征空间上的泛化误差，而其中的关键要素是在标记存在噪声的情况下刻画2个不同特征空间数据之间的差异.基于对分类器泛化能力的分析，本节进行了对应的算法设计，并通过深度神经网络进行了具体实现.

3.1 容忍标记噪声的演变差异

对于特征空间演变环境中的学习问题，由于演变阶段数据量较少，仅依赖演变阶段的标记数据来训练模型会容易出现严重的过拟合现象.因此，在这种情况下，利用旧特征空间上的标记数据变得至关重要.然而，由于新旧特征空间的维度不同，固定特征空间上的数据分布差异度量不再适用.此外，由于数据标记存在噪声，算法无法直接利用，因此学习者亟需建立容忍标记噪声的异质特征空间数据差异度量.

为了应对标记噪声，本文采用样本加权的方法恢复分类器在潜在无噪声数据上的真实损失.具体而言，针对每一轮的标记带噪数据集合，本文定义其加权经验损失为

其中样本权重αi定义为

基于式（1）的权重定义，考虑分类器在标记带噪数据上的加权损失，有引理1成立[6,26].

引理1.对于假设空间中的任一函数g∈G，给定权重α，分类器在标记带噪数据上的加权期望损失等于该分类器在潜在无噪声数据上的真实损失，即

证明：根据对期望风险的概率拆分，有：

其中式（6）是根据定义展开的，式（7）是改变数据分布后的概率重加权，式（8）的成立是因为标记噪声不改变样本特征的边际分布，式（9）的成立是根据噪声率的定义.对于式（9），考虑噪声正类标记的后验概率，有：

同理，考虑噪声负类标记的后验概率，有：

结合噪声正类标记的后验概率结果，可得式（5）成立.

证毕.

引理1证明了标记带噪数据上的加权经验风险在期望意义上等于分类器在潜在无噪声数据上的真实风险.因此，研究者可以通过对权重进行有效估计，设计对标记噪声具备容忍性的学习算法.

在通过样本加权处理标记噪声后，本文进一步考虑复用旧特征空间的标记数据，以辅助构建在新特征空间上具有泛化能力的分类器.在进行针对特征空间演变环境的学习理论分析之前，本文对学习算法的损失函数进行一定的假设.本文考虑损失函数ℓ是非负凸函数，并且满足以下类似利普希茨的平滑条件.

定义1.损失函数的σ-admissible性质.如果存在σ∈R+使得对于任意2个分类器g,g′∈G和对于所有样本(x,y)∈X×Y 有式（10）成立，则称损失函数ℓ对假设空间G 是σ-admissible的.

值得注意的是，式（10）中定义的具有σ-admissible性质的损失函数是较为常见的，包括平方损失、二次损失和许多其他损失函数.具体而言，满足σ-admissible性质的损失函数具有条件：对于M∈R+： ∀g∈G和∀x∈X，有|g(x)|≤M成立，且∀y∈Y，有|y|≤M成立.式（11）证明有界的最小二乘损失函数是满足条件的，其他损失函数可以通过类似的证明技术来证明.对于(x,y)∈X×Y 和g,g′∈G，有不等式（11）成立：

其中式（11）的成立是因为损失函数的M有界性质.至此，本文证明了有界最小二乘损失函数是σ-admissible的，其中.

本文基于损失函数的σ-admissible性质，通过构建数据差异的方式，利用旧特征空间上的标记数据辅助构建新特征空间上的分类器.与面向特征演变环境的机器学习的相关前沿研究相似，本文假设数据流中存在数据演变阶段，这一阶段的数据具有新旧2个特征空间的表示.基于旧特征空间上的标记带噪数据、新特征空间上的待预测数据，以及演变阶段数据，本文提出了容忍标记噪声的演变差异，衡量了特征演变环境中2个异质特征空间数据分布之间的差异.

定义2.容忍标记噪声的演变差异.令权重α如式（4）定义所示，对于特征演变环境中的标记带噪数据流，存在演变阶段数据的2个连续数据块与Ut+1，它们之间的演变差异定义为

其中g′∈Gt，g∈Gt+1是对应的2个分类器，对应着旧特征空间上标记带噪数据块的数据分布.

容忍标记噪声的演变差异衡量了标记带噪环境中新旧2个不同特征空间的差异，其中关键要素在于标记存在噪声，且数据的特征空间是不同的.定义2中，式（12）中等号右侧第1项通过演变阶段的对齐数据对齐了分类器g′∈Gt和g∈Gt+1，右侧第2项则通过分类器衡量了演变阶段数据与新特征空间上数据的差异.直观地说，容忍标记噪声的演变差异通过演变阶段数据建立了标记带噪环境中2个不同特征空间数据块的联系.

可以看到，本文提出的容忍标记噪声的演变差异将文献[32]所提的Y散度差异度量的概念推广到了特征空间演变、标记存在噪声的场景，并在特征不发生演变、标记无噪声时恢复成Y差异度量.值得注意的是，本文所提差异度量没有使用演变阶段数据的标记，因此具有对演变阶段标记噪声的容忍度.

基于所提容忍标记噪声的演变差异，本文复用了旧特征空间的标记带噪数据，分析了分类器在新特征空间上的泛化误差上界.可以证明，通过本文定义的容忍标记噪声的演变差异，学习者可以直接约束分类器在新特征空间上的泛化误差.

定理1.泛化误差界.假设损失函数ℓ是L利普希茨连续和σ-admissible的.对于任何δ＞0，至少以1-δ的概率，有：

证明：对分类器在新特征空间上的期望风险进行考察，有不等式成立：

其中，式（14）是基于Rademacher复杂度分析的泛化误差上界，式（15）对新特征空间上的目标函数取了最大值.式（16）同样是基于Rademacher复杂度分析的泛化误差上界.式（16）由3项内容构成：RDt′(g′)表示分类器在t轮的演变阶段数据上的真实期望损失；通过演变阶段数据建立了第t轮旧特征空间上标记带噪数据与第t+1轮新特征空间上待预测无标记数据之间的联系；衡量了分类器在第t+1轮特征空间数据上，演变阶段数据与新特征空间所有数据之间的差异.

这3项可以依次被约束.对于第1项，根据引理1，分类器在标记带噪数据上的加权期望损失等于分类器在潜在无噪声数据上的真实期望损失，因此可以将演变阶段数据的真实损失通过第t轮的标记带噪数据的加权经验损失和复杂度项进行上界.因此，有式（17）成立:

对于式（16）不等号右侧中的第2项，算法利用损失函数的σ-admissible性质，对齐不同特征空间上的分类器g′和g.根据损失函数的σ-admissible性质，有式（18）成立：

结合式（16）～（18），可以得证：

定理1证明了第t+1轮新特征空间上分类器的泛化误差可以被旧特征空间上标记带噪数据的加权经验风险及本文所提容忍标记噪声的演变差异所约束.本文所提的容忍标记噪声的演变差异通过样本加权的方式对抗了标记噪声，通过在演变阶段进行分类器对齐的方式桥接了不同的特征空间.如果样本标记是准确的，则可将α设置为1.通过对标记带噪数据进行重新加权，本文提出的算法可以获得对潜在真实损失的无偏估计（见引理1）.相比之下，启发式的对抗标记噪声的方法，如梯度裁剪[33]和丢弃大损失值样本[34]等，难以具备这样的能力，因此无法约束分类器在新特征空间上的期望损失的上界.

在证明定理1时，损失函数的σ-admissible性质至关重要.如定义1及式（11）中的分析所述，这一性质十分常见，适用于二次损失函数或者具有有界假设空间的损失函数.通过利用损失函数的σ-admissible性质，算法可以利用演变阶段的数据，将异质特征空间上的分类器g′和g进行对齐.在对齐分类器之后，即使标记带噪数据来自不同的特征空间，算法也可以复用旧特征空间的历史数据对当前数据进行学习.

3.2 算法设计

通过本文所提容忍标记噪声的演变差异，本文分析了分类器在新特征空间上的泛化误差上界.这一理论分析启发了本文的算法设计.本节将提出对应的算法，直接优化分类器在新特征空间上的泛化误差，构建具有良好泛化性能的分类器.算法首先对权重α进行估计，用以处理标记噪声；然后，算法将最小化标记带噪数据上的加权经验风险和容忍标记噪声的演变差异用以建立具有泛化能力的分类器.

基于本文所提演变差异和定理1中的泛化误差界，本文利用深度神经网络的特征提取能力，设计了容忍标记噪声的演变差异最小化算法LREDM.本文主要关注特征空间演变的2个连续数据块的学习问题，因此下文仅详细叙述在特征演变发生时对应的学习方案.

针对标记噪声，算法估计权重α后进行加权经验风险最小化.根据式（4）中权重的定义

算法需要估计条件概率和噪声率ρ±1.本文采用密度比估计（density ratio estimation，DRE）的方法来估计条件概率.密度比估计是一种显著减少核密度估计维度灾难的方法，它可以精确地估计高维变量的密度比.常用的3种密度比估计方法包括矩匹配法、概率分类法和比值匹配法.由于概率分类方法可能引入较大的近似误差，因此研究者在实际算法应用中更多地采用矩匹配或者比值匹配方法[35].其中，密度通常通过线性或非线性函数进行建模.如果选择的再生核希尔伯特空间比较适当，那么矩匹配和比值匹配方法的近似误差可以很小.这些方法在实践中被广泛证明了有效性[36-37].

对于条件概率，本文采用比值匹配法中被广泛应用的KLIEP法[30]来估计.给定样本和对应的带噪标记，KLIEP返回其条件概率.在获得样本的条件概率后，依照文献[26]中的结论，噪声率满足：

因此，本文通过对应类别在标记带噪数据上取最小条件概率的方法

来估计噪声率ρ±1.

在对权重α进行估计后，算法最小化分类器在标记带噪数据上的加权经验风险和容忍标记噪声的演变差异.定理1中的泛化误差分析对应优化目标

观察式（19）和式（20）可以发现，优化问题可以看作是一个极小极大优化问题，其中最小化分类器g,g′∈G最小化泛化误差，而最大化分类器ft+1∈Gt+1搜索演变差异的最坏情况.这类学习问题在基于对抗生成的迁移学习中被广泛研究，具有成熟的优化算法[38-39].因此，本文通过对抗网络DANN[38]来优化分类器的加权损失和容忍标记噪声的演变差异.具体而言，算法交替优化式（21）和式（22），直到损失收敛.

通过最小化旧特征空间上标记带噪数据的加权经验风险以及容忍标记噪声的演变差异，算法可以在新特征空间数据上获得一个具有良好泛化能力的分类器.由于权重α的优化问题和分类器g′和g的优化问题不是联合凸的，因此算法首先求解权重α来缓解标记噪声问题，然后优化极小极大优化问题.

容忍标记噪声的演变差异最小化算法的流程如算法1所示.

算法1.容忍标记噪声的演变差异最小化算法.

输入：每轮数据Lρt和下一轮待预测数据Ut；

输出：分类器g∈Gt+1.

①遍历t=1,2,…,T；

② 通过KLIEP算法估计式（4）中权重α；

③ 收到无标记数据Ut+1；

④ 通过DANN算法优化式（21）和式（22）的极小极大优化问题；

⑤ 获得gt+1并预测Ut+1；

⑥ 收到标记带噪数据并存储；

⑦结束.

4 实验与结果

本节测试了所提算法LREDM在现实应用场景中的性能表现.本节实验在合成数据集和多个现实应用数据集上将所提算法与前沿的基准算法进行了对比.具体而言，本节实验旨在回答3个问题：

1）合成数据分析.所提算法是否在数据标记带噪的情况下，在特征空间演变的环境中有效地建立了2个异质特征空间的差异度量.

2）基准算法对比.所提算法在各类现实场景中的数据集上的表现是否优于其他前沿的基准算法.

3）消融实验研究.所提算法的每个模块是否都能够对算法性能带来提升.

本节实验采用基准数据集，并通过对其进行修改，模拟特征演变环境的标记带噪数据流.为了满足实验数据对于动态特征空间的要求，本节实验将所使用的数据集原始特征空间进行划分.在每个时刻，实验使用基准数据集中不同的特征空间，并在相邻时间段中插入少量全特征空间数据，以模拟演变阶段数据，在2个特征空间上都具有特征表示.针对类别相关的标记噪声，本节实验考虑二分类问题，对于某一类样本，以一定概率将其标记翻转为另一个类别.需要注意的是，2个类别的标记翻转概率可以不同.为了测试算法的有效性，本节实验通过随机采样的方式和通过基准数据集生成不同特征演变的标记带噪数据流，并在不同数据流上测试算法的平均表现结果.本节对每个数据集进行随机采样，生成10条数据流，并基于这10次结果的平均值和标准差来报告最终的实验结果.针对每条数据流，本节考虑发生1次特征空间演变，并在新特征空间上测试算法的实验结果.

本文在包括RFID，Amazon，Reuters数据集以及其中包含的子数据集的公开数据集上进行试验，这些数据集分布在多个现实应用领域.

1）RFID数据集[3].该数据集由传感器收集的物体RFID数据（特征）和物体的实际位置（标记）组成.由于物体不断到达，传感器收集的RFID数据形成了数据流.在传感器达到使用寿命之前，学习者会在旧传感器附近放置新的传感器，因此数据流的特征空间发生了演变.在本节实验中，位置索引被分为2类以生成相应的标记.对于旧特征空间数据标记，本节实验将其标记以10%的概率进行均匀翻转以模拟标记噪声.根据数据的时间戳信息，数据流的前40%是旧特征空间数据，接下来的20%是演变阶段数据，最后40%是新特征空间数据.

2） Amazon数据集[40].该数据集包含用户在2006—2008年对亚马逊上产品的评价和对应用户的质量评分.本节实验采用了该数据集中的3个子数据集，分别是Books，Movies和CDs.学习者希望根据用户的评价（特征）判断用户的质量（标记）.用户不断使用这个平台，形成了数据流.随着时间的推移，旧的产品下架，新的产品上架，因此数据流的特征空间发生了演变.本节实验将部分活跃用户对历史商品和当前商品的评分作为特征空间演变数据流中的数据演变阶段.实验根据用户评价的质量将用户分为2类，从而生成了一个二分类任务，并添加了10%的均匀标记噪声.根据数据的时间戳信息，数据流的前40%为旧特征空间数据，接下来的20%是演变阶段数据，最后40%是新特征空间数据.

3） Reuters多语言数据集[41].该数据集包含5种语言的约一万篇文档.由于每种语言特征表示不同，因此同一文档的不同翻译版本对应着不同的特征空间，本节实验以此模拟特征空间演变的数据流.本节实验将旧特征空间数据的20%设置为演变阶段数据，并在新特征空间找到其对应表示.对旧特征空间数据标记，本节实验将文本标签分为2类，并将标记以10%的概率均匀翻转，用以模拟标记噪声.所有文档都使用TF-IDF特征表示，本节实验基于文档的TF-IDF特征进行主成分分析（PCA），提取了文档的主要特征.实验部分所用数据集的相关统计信息如表2所示.

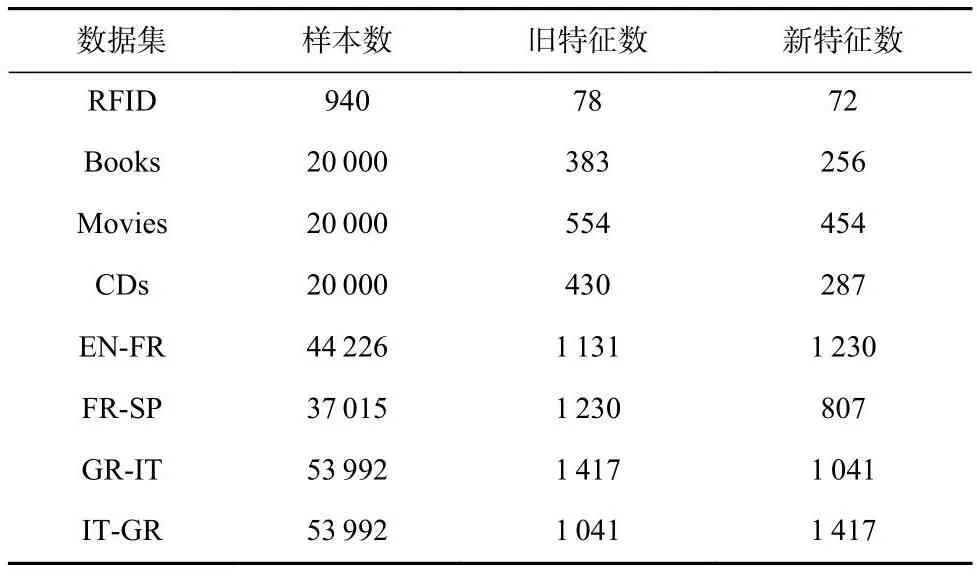
Table 2 Statistics of the Datasets表2 数据集的统计信息

对于LREDM算法的实现，本节实验将采用2个神经网络分别作为最小化分类器和最大化分类器，每个网络都包含5层全连接层，并以ReLU函数作为激活函数.本节实验将使用衰减学习率的在线随机梯度下降（SGD）对模型进行训练，学习率设置为0.004，正则化权重衰减为0.005.

4.1 合成数据分析

本节首先在合成数据上对所提算法进行分析，测试容忍标记噪声的演变差异在度量异质特征空间的标记带噪数据块上的度量性能.

在本节实验中，采用高斯分布生成数据，可以通过调整均值和方差来控制数据的差异度.因此，可以通过对比算法对不同差异度的数据集的处理效果，来评估算法的差异度量能力.直观上来看，算法的差异度量能力越强，就越能够准确反映数据之间的真实差异.因此，本节实验将通过对合成数据进行分析，测试所提算法在度量异质特征空间的标记带噪数据块上的度量性能.

本节实验通过对高斯分布进行采样生成数据，合成了3组数据集.每组数据集都包括2个不同特征空间的数据集合：一个是三维的数据集合，另一个是二维的数据集合.为了模拟特征空间的演变，本节实验将二维数据作为旧特征空间数据，将三维数据作为新特征空间数据.同时，二维数据和三维数据分别从不同均值的标准高斯分布中进行采样，以模拟不同差异度的学习任务.

1）任务1：二维数据中（旧特征空间），正类数据从Nx([1,1])中生成，负类数据从Nx([-1,-1])中生成；三维数据中（新特征空间），正类数据从Nx([1,1,1])中生成，负类数据从Nx([-1,-1,-1])中生成；

2）任务2：二维数据中（旧特征空间），正类数据从Nx([1,1])中生成，负类数据从Nx([-1,-1])中生成；三维数据中（新特征空间），正类数据从Nx([1,-1,1])中生成，负类数据从Nx([-1,1,-1])中生成；

3） 任务3：二维数据中（旧特征空间），正类数据从Nx([1,1])中生成，负类数据从Nx([-1,-1])中生成；三维数据（新特征空间），正类从Nx([-1,-1,-1])中生成，负类数据从Nx([1,1,1])中生成；

通过计算，可以发现在三维特征空间中，从任务1到任务3，同类数据的类中心距离不断增大，因此可以认为数据的差异度在一定程度上是不断增大的.对于每个任务，本节实验生成了1 000个旧特征空间上的三维样本和800个新特征空间上的二维样本，并随机选择了200个样本作为演变阶段的数据.

下文将对比不同算法的数据差异度量能力.当数据特征空间发生演变时，一个自然的做法是通过演变阶段数据建立2个特征空间之间的映射，以复用旧特征空间上的数据和学习模型[3].直观上来说，如果新旧特征空间上的数据十分相似，那么映射误差应该很小，即算法可以通过映射矩阵将新旧特征空间上的数据接近无损地转换.为了与本文所提演变差异进行对比，下文将基于映射方法建立的新旧特征空间数据之间的重构误差称为映射误差.记学习后的映射函数为M，映射误差可表示为：

映射误差衡量了映射函数的数据恢复能力.假设存在一个完美的映射函数，它可以将新旧特征空间之间的表示一一映射，那么通过这个映射函数，算法可以完美恢复出新特征空间数据在旧特征空间上的表示，即映射误差为零.与演变差异的度量方式类似，当数据越相似时，映射误差越小.对于本文提出的基于演变差异最小化的算法，本文直接采用演变差异作为衡量指标，度量所提算法所构建的新旧特征空间之间的数据差异.

本节针对3个合成任务测试了LREDM算法和FESL算法的性能.由于数据存在噪声，本文统一采用IW算法对标记带噪数据进行加权处理后提交对比算法.由于这2个衡量方式的量纲不同，无法直接比较，因此本节将所有结果进行归一化后，通过图2展示它们在这3个任务上的差异.

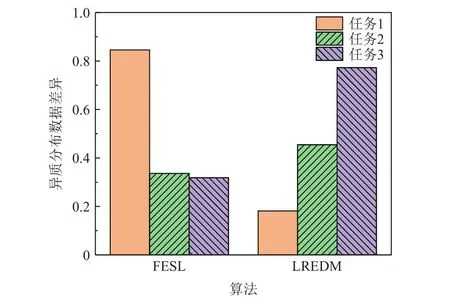
Fig.2 Date relative discrepancy exhibited by FESL and LREDM图2 FESL和LREDM展示的数据相对差异

总体而言，本文提出的LREDM算法表现更加准确.具体来说，任务1是3个学习任务中最简单的，因为新特征空间数据只是旧特征空间数据的边际分布.图2表明任务1的演变差异明显小于任务2和任务3，这符合直觉.相比之下，FESL算法在任务1中报告了最大的映射误差.对合成数据的分析表明，LREDM的演变差异能够在数据标记存在噪声的情况下恢复异质特征空间数据块之间的差异，并为特征空间演变环境下的标记带噪数据学习问题提供了更准确的差异度量方法.

4.2 基准算法对比

本节对所提的LREDM算法在现实应用中的表现进行了测试，主要考虑标记带噪数据和特征空间演变的情况.与此同时，本节还将LREDM算法与前沿算法的性能进行了比较.

本节实验在3个数据集上模拟了8个标记带噪数据学习任务，并与6种前沿基准算法进行了比较.这些任务都涉及特征空间的演变.其中，FESL，EDM和OLVF算法是在特征空间演变环境下的前沿学习算法，能够有效处理特征空间变化下的学习任务.然而，这些算法并未考虑标记噪声对学习的负面影响.因此，本节实验添加了额外的标记噪声校正机制，以进行公平比较.具体而言，本文采用重要性加权（Importance weighting, IW）机制和使用高置信度（high confidence, HC）样本机制对基于映射的代表性算法FESL算法进行了调整，并将这2种算法分别命名为FESL+IW和FESL+HC.对于FESL+IW算法，本节实验首先对旧特征空间的标记带噪样本进行重加权，然后使用FESL算法进行学习；对于FESL+HC算法，本节实验首先在旧特征空间上训练一个分类器，清除置信度低于阈值的标记样本，然后使用FESL算法进行学习.除了这2种算法外，本节实验还引入了另一个基准算法IWTS进行两阶段学习.与LREDM算法相同，IWTS算法采用了分块学习预测的方法，并直接结合了特征演变数据学习和标记带噪数据学习的方法作为本文研究问题的基准算法.IWTS算法首先使用IW在旧特征空间数据上训练模型，然后为演变阶段数据赋予伪标记，基于演变阶段的伪标记数据训练第2阶段模型，并对新特征空间样本进行预测.

表3中展示了LREDM算法与对比算法在各个实际应用数据集上的平均准确率比较.实验结果表明，LREDM算法在8个学习任务中均取得了最高的平均准确率，这表明LREDM算法是在特征空间演变环境中针对标记带噪数据学习任务的一种可行方案.相比于基于映射的算法，LREDM算法具有更好的性能，因为它更准确刻画了异质特征空间中标记带噪数据块之间的差异，并且直接最小化期望风险的上界.此外，实验结果还表明，LREDM算法总是优于TSIW算法.这是因为在现实世界场景中，演变阶段的数据通常较少，很难学到准确的映射函数.

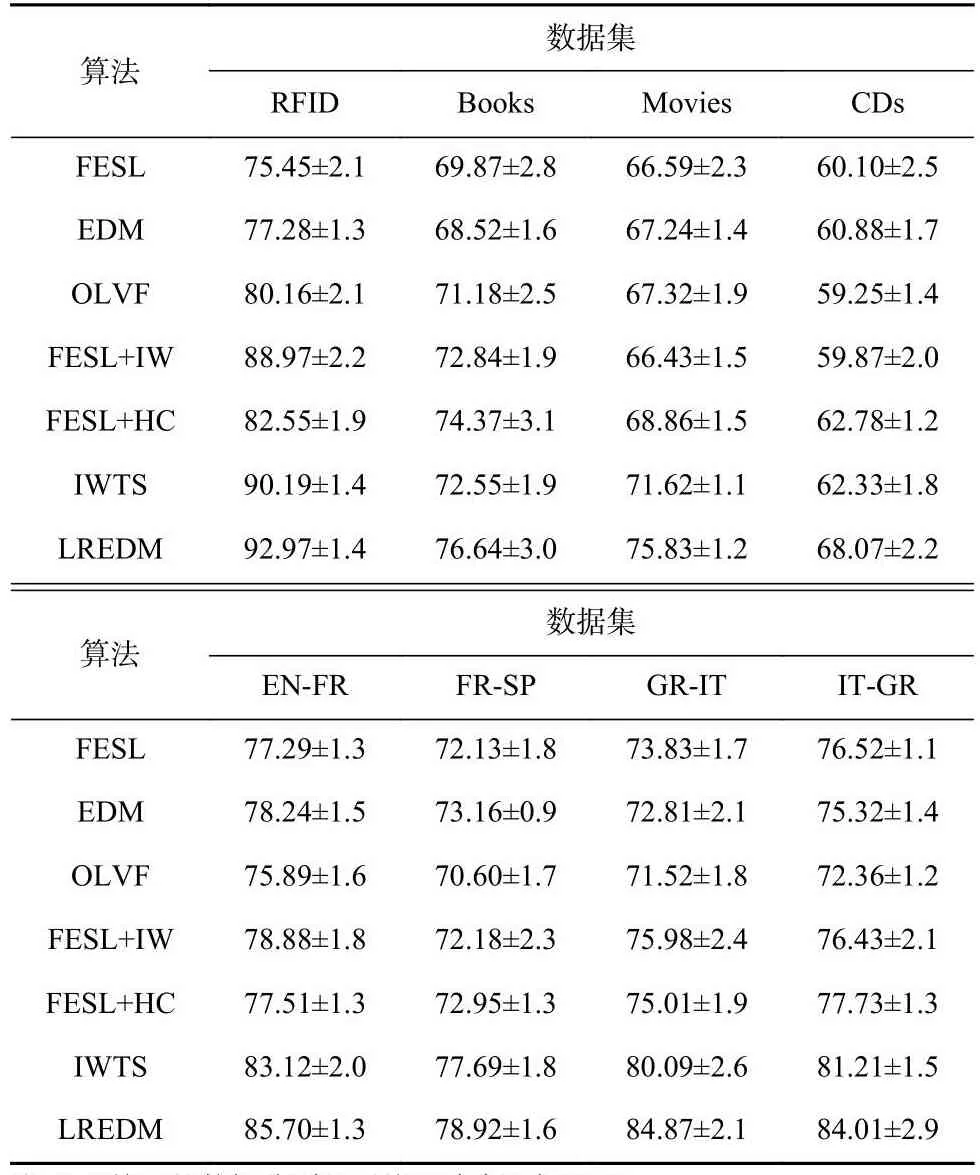
Table 3 Average Accuracy and Standard Deviation of Seven Algorithms on Different Datasets表3 7种算法在不同数据集上的平均准确率与标准差%

本节实验还在语言数据集上进行了实验，测试了LREDM算法在文本分类场景中的性能.表3中EN-FR，FR-SP，GR-IT，IT-GR这4个数据集展示了LREDM算法与前沿对比算法在文本数据模拟的学习任务上的实验结果.实验结果显示，在4个文本分类任务中，LREDM算法取得了最高的平均准确性，验证了该算法在文本类现实应用中的有效性.

本节实验同样测试了LREDM算法在不同噪声率下的有效性.该实验在Movies数据集和EN-FR数据集上进行，并采用不同的噪声率来评估LREDM算法的性能.表4展示了LREDM算法和IWTS算法在4种不同噪声率下的平均准确率和标准差.例如，“0.3/0.1”表示将正类数据以30%的概率错误地标记为负类，同时将负类数据以10%的概率错误地标记为正类.IWTS算法作为对比算法在基准对比实验中表现出色，因此也在表4中列出.如表4所示，LREDM算法在不同噪声率下均取得了更好的实验效果，验证了LREDM算法在不同噪声率环境下的鲁棒性.

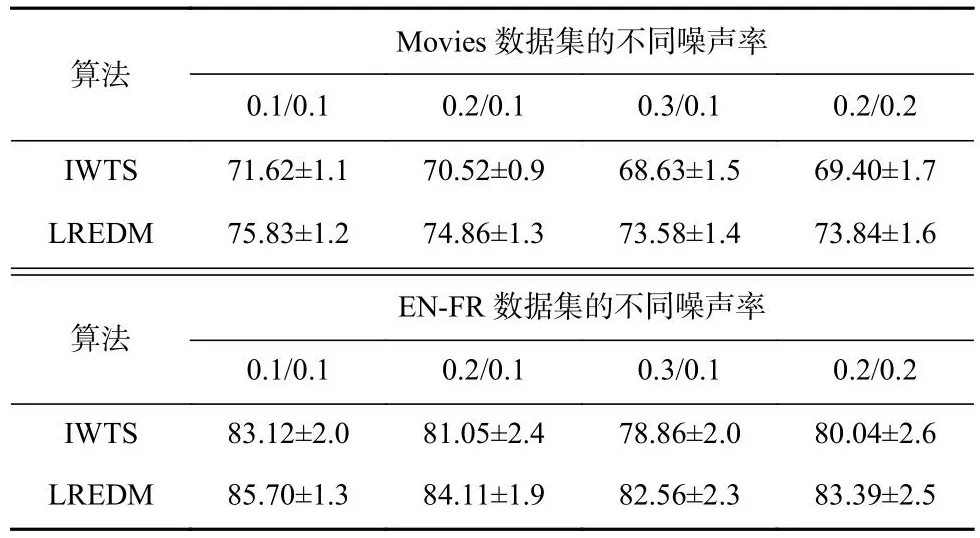
Table 4 Average Accuracy and Standard Deviation of Two Algorithm on Datasets with Varying Noise Rates表4 2种算法在2种数据集上不同噪声率下的平均准确率与标准差%

4.3 消融实验

本节实验在Reuters多语言数据集上对LREDM算法的每个组成部分进行了有效性测试.LREDM算法中的关键模块包括对标记带噪数据权重的估计（即噪声率估计）、对标记带噪数据上的加权经验风险和容忍标记噪声的演变差异的最小化.其中，与权重估计相关的模块是IW算法，没有加入IW算法的对比方案将标记带噪数据的标记视为准确的，并直接进行优化.在消融实验中，本文所提算法被记作LREDM（加权）；而不加入IW模块（不对标记噪声进行特殊处理）的对比方案被记作LREDM（不加权）.

本节实验测试了LREDM算法在Reuters多语言数据集上6对不同语言之间进行特征空间演变的标记带噪数据学习.图3展示了LREDM算法在这些任务中的加权经验风险、容忍标记噪声的演变差异和平均准确率随迭代次数的变化情况.实验结果表明，随着演变差异的减少，LREDM算法在这6项任务中的平均准确率均有所提高，这验证了最小化容忍标记噪声的演变差异对于特征空间演变环境中标记带噪数据学习问题的重要性.LREDM（加权）算法通过学习权重对标记带噪数据进行去噪，然后通过最小化容忍标记噪声的演变差异来减小异质特征空间的数据差异.实验结果显示，与不带标记噪声进行处理的对比方案LREDM（不加权）相比，通过应用IW算法学习权重的LREDM（加权）算法获得了具备更好泛化性能的分类器.对于存在标记噪声的学习问题，IW算法可以缓解标记噪声带来的影响.因此，消融实验的结果验证了本文所提的容忍标记噪声的演变差异度量的有效性，并验证了LREDM算法中每个组件的有效性.

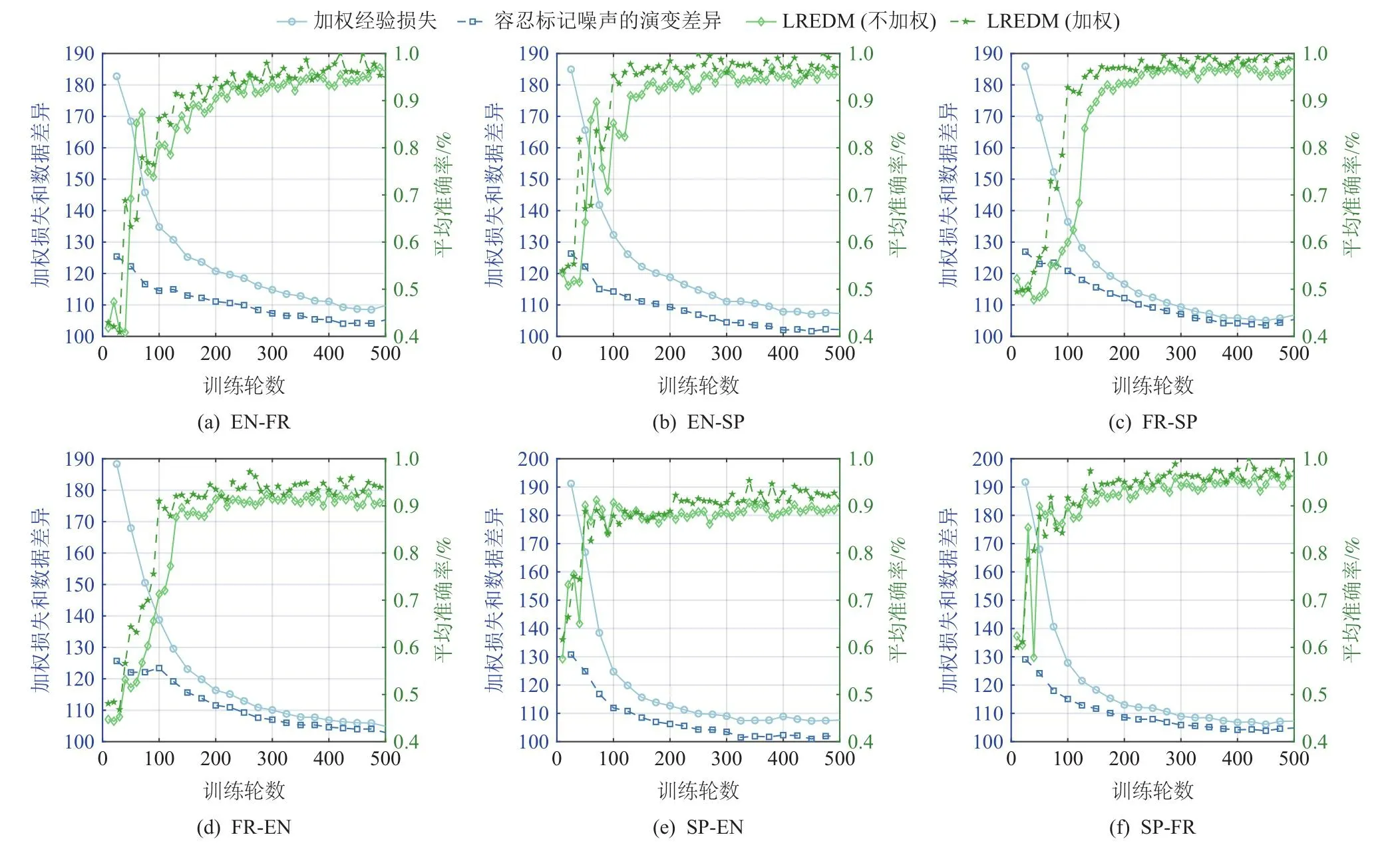
Fig.3 Weighted empirical risk, label noise robust evolving discrepancy and average accuracy of LREDM algorithm on six groups of experiment simulated by Reuters dataset图3 LREDM算法在Reuters数据集模拟的6组实验上的标记带噪数据的加权经验风险、容忍标记噪声的演变差异和平均准确率

因此，通过对LREDM算法在Reuters新闻分类任务上的消融实验，本节验证了LREDM算法中每个组件的有效性.

5 结 论

本文研究了在特征空间演变环境下的标记带噪数据学习问题，这个问题在实际应用中非常重要且普遍存在.由于数据标记存在噪声并且特征空间可能演变，如何设计学习算法，有效利用旧特征空间中的标记带噪数据，使得分类器在新特征空间上具有良好的泛化能力，是一个极具挑战性的问题.为了应对这一挑战，本文提出了容忍标记噪声的演变差异来建立具有不同特征空间的连续数据块的差异度量，并且分析了分类器在特征空间演变的标记带噪数据流上的泛化误差.基于所提理论，本文设计了一种名为LREDM的演变差异最小化算法，并使用深度神经网络进行实现.通过对合成数据的分析研究，本文验证了所提出的容忍标记噪声的演变差异可以建立异质特征空间的标记带噪数据块之间的差异度量.同时，多个实际应用数据的实验表明了本文所提出的算法在性能和稳健性方面的优越性.

本文未来的工作主要集中在2个方面：首先，当前所提出的算法在每一轮中需要求解一个极小极大化的优化问题，这一求解过程耗时较多.因此，如何进一步降低算法的运行时间，以更好地适应数据流学习是下一步重要的研究方向.其次，本文考虑了与样本无关的均匀标记噪声，但现实应用中的标记噪声往往更为复杂.因此，如何建立更加有效的求解算法以应对现实应用中复杂的标记噪声，是未来的重要研究课题.

作者贡献声明：张震宇负责提出模型，完成实验、初稿写作和论文修改；姜远负责写作指导和修改审定.