基于多轮修正噪声标签的神经网络分类框架

王学刚,王玉峰

(南京邮电大学 通信与信息工程学院,江苏 南京 210003)

0 引 言

最近,基于监督学习的深度神经网络在诸多领域取得了巨大的成功[1],但是带噪声标签的训练样本,对其性能产生很大影响[2-4]。噪声标签在数据收集和标注过程中是自然存在的。雇佣专业人员来标注数据其成本非常高,因此实际中更多采用的做法是使用众包平台来完成标注工作[5],如此虽降低了成本,但标注质量通常较差[6-7];另外在一些特殊领域(如医学成像),其数据标注工作非常复杂,即使专家标注也可能因为标注者的主观性或缺乏经验而产生噪声标签[8]。

对噪声标签对网络的消极影响问题,目前的解决方案包括建模标签转移模型和清除带噪数据等,其在相应的实验仿真中都展现出了一定的抗噪声性能,同时也暴露出了一定的局限性。基于建模标签转移模型的方法往往通过增加额外网络层来建模标签转移关系或利用标签转移矩阵来矫正损失函数,该类方法依赖于对标签转移关系的准确建模或标签转移矩阵的高精度估计,该工作通常存在一定的挑战;其次,基于清除带噪数据的方法是将带噪数据进行剔除或给予较小的权重,然而这样的操作不但减小了数据集的规模,并且可能忽略掉一些重要数据、破坏数据集的完整性。

针对已有方法存在的问题,该文提出了一种基于多轮修正对抗噪声标签的神经网络分类框架MCNN。具体而言,贡献主要在以下3个方面:

首先,提出了一种估计数据集标签转移矩阵和噪声率的方法。与之前的工作相比,该方法不需要引入额外的人工标注成本。

其次,根据“小损失”准则提出了一种筛选带噪数据的方法,同时还提出了一种有效的方法来修正噪声标签。与之前的工作相比,提出的筛选带噪数据方法不依赖于特定的系统或网络,同时对筛选出的噪声标签进行修正,保留了数据集的完整性。

最后,在多个真实数据集上对所提出的MCNN进行了训练测试,表明MCNN能够有效地对抗噪声标签,提升模型的分类性能。

1 相关工作

近年来,缓解噪声标签对神经网络影响的方法有很多。Reed等[9]提出了一种样本重标注的方法Bootstrapping,使用神经网络预测值和原始标签的线性组合对全体样本进行重标注,然后进行反向传播训练网络,缺点在于在大噪声率情况下效果不佳。余等[10]也提出了一种基于重标注样本来对抗噪声标签的方法,然而局限性在于其主要适用于“二元分类”任务。

Jindal等[11]采用增加“噪声适应层”来构建标签转移模型。通过在基本网络的softmax层后面增加一个K*K维的线性约束层来建模标签转移模型,并使用正则化来惩罚线性约束层的迹以使线性约束层逼近于实际标签转移模型,然而该方法的缺点是对数据的噪声类型有一定限制。

与在基本网络后附加“噪声适应层”的方案不同,文献[12-14]将建模标签转移模型和训练分类器解耦,代表性的工作有:Patrini等[12]提出了“前向纠正”法F-correction来矫正损失函数。首先,利用估计的标签转移矩阵与数据样本的网络预测值做矩阵乘积,然后,将所得结果与标签值计算交叉熵损失以此达到矫正损失的目的,但估计标签转移矩阵通常存在误差,数据量较大时存在误差累积问题。

Malach等[15]在观察利用带噪声标签数据训练网络时发现,在整个训练过程中网络倾向于在拟合带噪声标签的数据之前先拟合带正确标签的数据,因此在网络的整个训练过程中平均损失较大的数据更大概率是带噪声标签的数据,该训练特性称作“小损失”原则。

之后利用“小损失”原则产生了一系列对抗噪声标签的方法[16-18],代表性的工作有:Han等[16]提出了一种名为Co-teacher的联合学习方法,该方法同时训练两个不同的网络,两个网络都基于本网络中样本的损失值移除可能的带噪声标签数据,然后将去噪后的数据传给另一个网络做下一次迭代更新,然而该方法在训练后期存在网络“靠拢”问题,另外将含噪数据移除有可能意外地去除一些有用样本,同时假设数据集的噪声率是已知的不符合真实的任务场景。

2 MCNN框架和组成部分

2.1 MCNN基本模型结构

如图1所示,MCNN网络框架在每轮修正中包括4个步骤:估计标签转移矩阵、估计数据集的噪声率、筛选可能的带噪数据和自适应修正带噪数据中的标签。注意,在每一轮修正中,MCNN都更新所训练的DNN网络以及所使用的数据集。

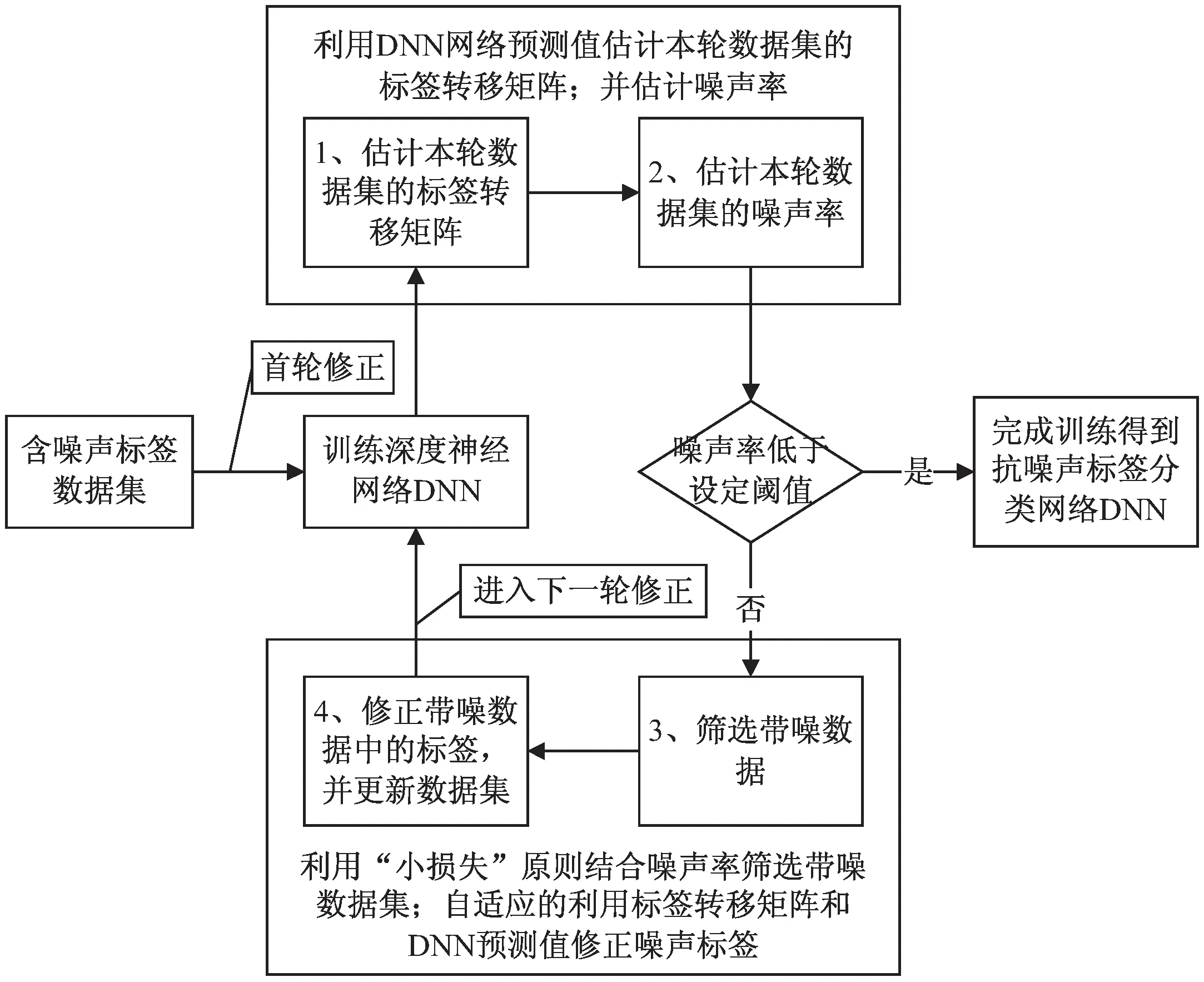
图1 MCNN基本结构

下面详细描述了MCNN的各个主要组成部分。

2.2 估计标签转移矩阵

标签i的“锚点样本”xi本质上为该标签的“完美样本”,即神经网络对“锚点样本”xi的输出预测值满足如下条件:

p(y=i|xi)→1,xi∈X,X∈D

p(y=j|xi)→0,i≠j

其中,D={X,Y}代表训练数据集,X代表数据集中的全体样本。因此,该文将数据集所有样本中最大概率标注为某类标签的样本近似看作该类标签的“锚点样本”,即:

在获取到各类标签的“锚点样本”后,标签转移概率可估计如下:

相应的标签转移矩阵估计如下:

在MCNN的多轮修正过程中,每一轮都估计当前训练数据集Dt的标签转移矩阵Pt,其中t表示当前训练的轮数。

2.3 计算加权平均噪声率

带数据集的噪声率在诸多任务场景中通常是未知量,然而清除带噪数据需要噪声率作为指标。现有的方案[18]中利用专业人员标注小批量数据并进行专家比对计算噪声率。进而根据小批量数据的噪声率估计整体数据集的噪声率,估计的质量取决于小批量数据的抽样和选择方法,且专业人员的引入增加了任务的额外代价。

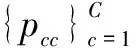
B=A×P

rw=W•R

多轮修正过程中,针对第t轮的训练数据集Dt,其加权平均噪声率rw, t可利用其标签转移矩阵Pt求得。

2.4 筛选带噪数据

“小损失”准则表明利用各数据在训练过程中的损失值可以帮助筛选带噪数据。依赖单一网络的数据损失存在“意外记忆”问题。Han等[16]提出了一种双网络联合学习的方法,然而该方法的缺点在于网络结构比较复杂。

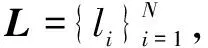
在多轮修正的第t轮修正中,依据上述方法将本轮的训练数据集Dt按照加权平均噪声率rw, t划分为带正确标签的数据集Dt,l和带噪声标签的数据集Dt,n,其计算公式如下:

Dt,l=Dt*(1-rw, t)

Dt,n=Dt*rw,t

考虑到筛选存在的误差,在Dt,n中包含的数据包括真实带噪数据量St和意外筛选数据量Ut,且有:

Dt,n=St+Ut

此时,数据集中实际的带正确标签的数据量可记作Dt,r,有:

Dt,r=Dt,l+Ut

2.5 联合修正噪声标签

基于清除带噪数据的方法采取将带噪声标签的数据从训练数据集中清除或给予较小的权重[18],然而该操作有可能意外地去除或忽略一些有用样本[6],从而影响网络的最终性能。为此,结合标签转移矩阵和神经网络的输出预测值,该文提出了一种针对噪声标签的联合修正方法。

在大噪声率下有:

在小噪声率下有:

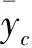
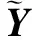
其中,a为超参数,其值的选取依赖于数据集的噪声类型。权重因子满足在数据集的噪声率较大时,使修正值主要依赖于标签转移矩阵修正值;在噪声率较小时,使修正值主要依赖于网络预测修正值。根据数据集的噪声率变化自适应地调整两个修正值的贡献度以提高修正的准确性。

在多轮修正的第t轮修正中,利用上述方法对筛选出的带噪声标签数据集Dt,n进行标签修正,其中对于真实带噪数据量St,若假设修正准确率为λt,则该轮正确修正的数据量为λt*St;同理针对意外筛选数据量Ut,若假设意外改错率为μt,则意外纠错数据量为μt*Ut。

因此,由上述可求得第t+1轮修正中的训练数据集Dt+1中实际的带正确标签的数据量,记作Dt+1,r,其中:

Dt+1,r=Dt,r+λt*St-μt*Ut

且在标签修正过程中正确修正的数据量通常远大于意外纠错数据量,即:λt*St>μt*Ut,所以有:

Dt+1,r>Dt,r

综上所述,MCNN的修正算法能够有效地逐轮增加训练数据集中的带正确标签数据量,符合网络设计预期。

2.6 多轮修正的截止条件

该文采取了多轮修正的策略,以尽可能地改善数据集的标签质量水平。多轮修正截止条件的设定可以有多种方法。

实验发现当数据集的噪声率低于10%时,继续降低噪声率,训练的网络性能无显著提升。因此,将截止条件设置为:估计所得数据集的噪声率低于10%时截止训练。

需要明确指出的是:提出的MCNN是一种通用的基于多轮修正使用噪声标签数据进行分类的网络架构,不依赖于所使用的多轮修正截止条件。

3 实 验

3.1 数据集说明

为了验证MCNN的性能,在多个数据集上进行了实验,包括MNIST、FASHION_MNIST和CIFAR-10。

3.2 人工加噪

为了获得相应的带噪数据,该文采取了三种广泛使用的加噪方式对数据集进行人工加噪。

(1)对称噪声(Symmetric Noise)[8]:每一类标签以相同概率转换为其他可能的标签。

(2)成对翻转噪声(Pair-flip Noise)[19]:将某一类标签按照某个概率随机替换为其他某一类标签。

(3)模拟真实世界噪声(Simulated Real-words Noise)[20]:考虑数据集的样本特征选取其中最有可能混淆的类别并在它们之间进行替换。

注意在对称噪声(Symmetric Noise)中,每一类标签以相同概率转换为其他可能的标签,转换概率和为噪声率;针对成对翻转噪声(Pair-flip Noise)和模拟真实噪声(Simulated Real-world Noise),如果人工加噪率超过50%即噪声标签的数目超过正确标签的数目,则网络将无法学习到数据集的有效信息[16]。因此,针对不同的噪声类型,该文选取了不同的噪声率进行实验,具体如表1所示。

表1 人工加噪过程中各类型噪声的噪声率

3.3 对比方案

在对比实验中,将MCNN和多种最新的基于噪声标签训练分类神经网络的方案进行了全面深入的对比。对比方案描述如下:

Direct-Training:直接利用带噪数据集训练神经网络,是最基本的对比标准,同时可以直观地看到噪声标签对神经网络性能的影响。

Bootstrapping[9]:使用网络的预测值和原始标签的加权组合作为样本的新标签,然后进行反向传播训练网络。

F-Correction[12]:估计带噪数据集的标签转移矩阵,然后利用该矩阵修改基本分类网络的输出,之后利用修改后结果和噪声标签构成的损失函数训练分类器来达到抗噪声标签的效果。

Co-Teacher[16]:训练两个神经网络。每个网络指导另一个网络在训练中筛除掉可能附有噪声标签的数据,以减小噪声标签对网络参数的影响。

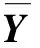
在F-Correction中,该文利用估计所得的标签转移矩阵P修改分类网络的输出预测值,具体地:

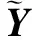
其只利用矩阵元素的相对大小而不做矩阵乘法,误差容限较大,所以具有一定的优越性。

在Co-Teacher方案中,将原始训练数据集Dt中的带噪声标签数据Dt,n依据“小损失”准则筛选出来并去除,并利用剩余的带正确标签的数据集Dt,l训练网络,其缺点在于将Dt,n去除的做法严重削减了样本数量,在大噪声率条件下表现较差。该文提出的网络框架则是将带噪声标签数据Dt,n逐轮修正,有效地扩大了带正确标签的数据集Dt,l,因此在大噪声率条件下具有一定的优势。

综上所述,提出的MCNN网络框架较现有的方法具有一定的优势。

3.4 实验设置

(1)针对不同的数据集,选取了不同神经网络模型进行训练,具体信息如表2所示。

表2 数据集训练所用分类网络

(2)关于筛选带噪数据步骤中周期性改变网络的学习率参数的相关设置:循环训练可解决网络的“意外记忆”问题,然而循环次数过多会增加训练时长,平衡之下选取循环次数为3。

(3)关于修正策略的权重因子中参数的选取,其依赖于数据集的噪声类型。鉴于在相同噪声率条件下,在对称噪声的数据集上训练的网络具有较好的分类性能,而利用带有成对翻转噪声和模拟真实噪声的数据集训练的网络分类性能则较差,因此在对抗对称噪声时a选取2;在成对翻转噪声和模拟真实噪声时a选取0.7。

3.5 性能比较指标

从分类精度上将提出的方案和各种对比方案进行了比较和评估。模型在测试集上的分类精度定义为:

表3给出了各种方案在MNIST、FASHION-MNIST和CIFAR-10的测试集上的分类精度比较,其中S代表对称噪声,P代表成对翻转噪声,S-R代表模拟真实噪声,相应的数字代表人工加噪的噪声率。

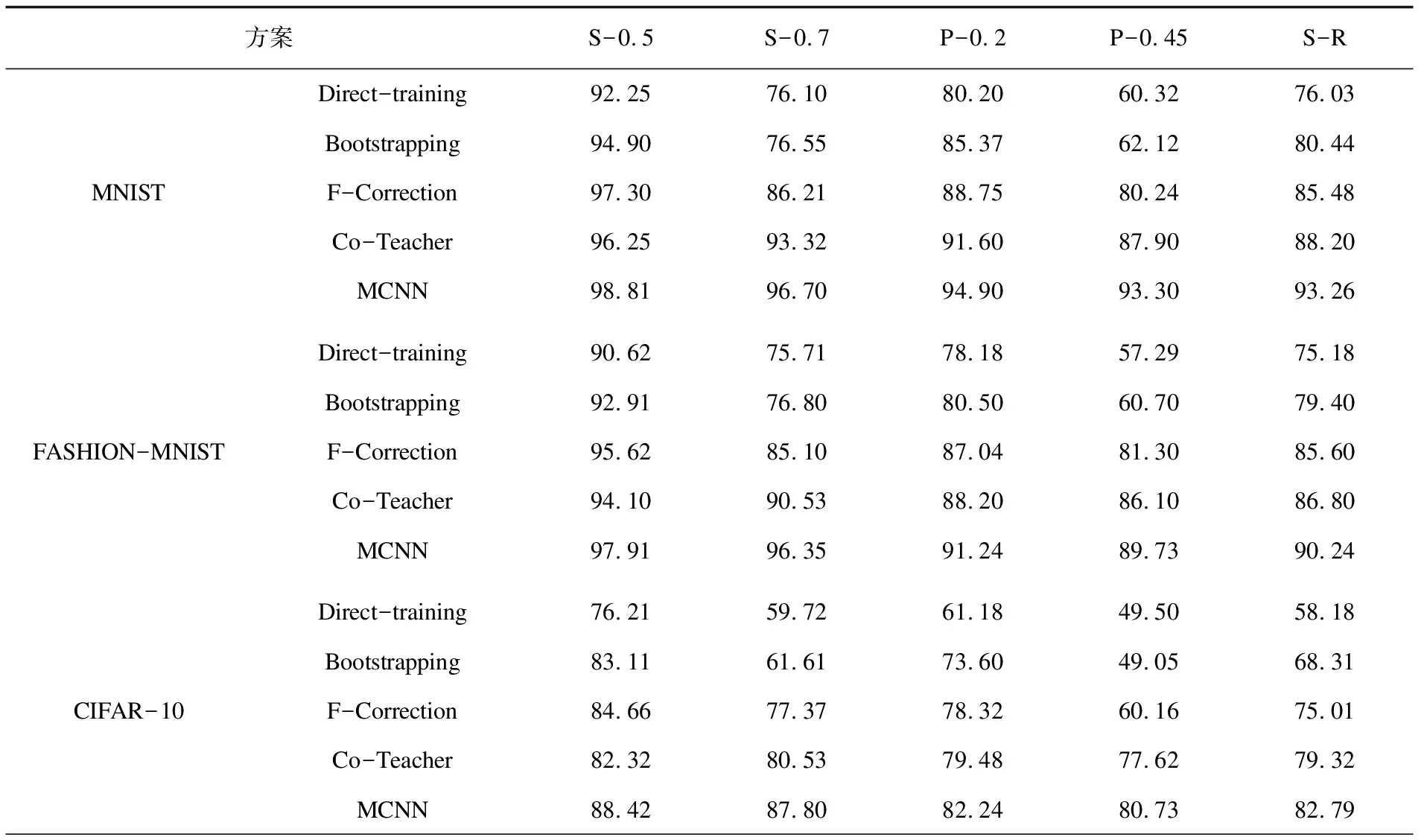
表3 各种方案在MNIST、FASHION-MNIST和CIFAR-10的测试集上的分类精度比较 %

3.6 实验结果与分析

从表3中可以得出如下结论:

(1)MCNN在多种不同的噪声类型和DNN网络结构下都取得了最好的分类性能,充分说明了该方案的优越性和健壮性。

(2)由表3可以看出,Bootstrapping[9]在小噪声率情况下如S-0.5和P-0.2表现良好,而在大噪声率情况如S-0.7和P-0.45则表现较差,原因在于在大噪声率下,网络的预测值可信度较低,Bootstrapping将其与噪声标签相组合不仅无法改善标签质量,甚至还可能污染原本正确的标签。提出的MCNN只对筛选出的错误标签进行处理,有效避免了污染正确标签的问题,因此最终的模型性能优于前者,针对各类数据集在S-0.7和P-0.45上,MCNN最终的模型在分类精度上有超过20%的提升。

(3)相比于F-Correction[12],前者利用标签转移矩阵与数据样本的网络预测值做矩阵乘积,然而标签转移矩阵在估计时通常存在误差,在数据集数据量较大时,存在误差积累。该文提出的MCNN只单次利用标签转移矩阵推测加权平均噪声率误差累积较小;同时,在标签修正阶段,该文只利用矩阵元素的相对大小来提供一个噪声标签修正值而不做矩阵乘法,误差容限较大。因此,最终训练的模型在各类型噪声下分类精度都有一定的提升。

(4)Co-Teacher[16]通过清洁数据集来对抗噪声标签,在小噪声率条件下,Co-Teacher和MCNN大体上性能相同,都实现了较好的抗噪声性能,例如在MNIST和FASHION-MNIST上针对S-0.5都达到了超过90%的分类精度。而在大噪声率条件下,MCNN的性能优于Co-Teacher,原因在于Co-Teacher采用将带噪数据清除,在大噪声率条件下严重削减了样本数量,而MCNN则采取将噪声数据修正减少了数据量的损失,因此在大噪声率下模型的性能优于前者,例如在CIFAR-10数据集上针对S-0.7在分类精度上有接近7%的提升。

3.7 MCNN的可行性分析

提出的MCNN能够改善数据集质量的因素主要在于两点:错误标签筛选和多轮修正。关键之处在于以下两个方面:

(1)MCNN能够实现对数据集标签转移矩阵的准确估计,同时可以精确地估计数据集的噪声率用以为筛选带噪数据提供基准。

(2)MCNN能够实现对带噪数据的准确筛选即具有较高的带噪数据筛选精度,并且提出的修正方法可以实现对标签的“正向修正”。

3.7.1 仿真结果

选取MCNN在MNIST数据上针对模拟真实噪声(S-R)的实验结果详细阐述MCNN的可行性。为此,采用如下5个MCNN运行过程中的中间性能量度来定量展示MCNN提升数据集质量的两个关键方面。

(1)标签转移矩阵估计误差。定义如下:

(2)噪声率估计误差。定义如下:

‖噪声率实际值-加权平均噪声率‖1

(3)带噪数据筛选精度。定义如下:

(4)修正准确率。定义如下:

(5)意外改错率。定义如下:

图2和图3给出了在MNIST数据集上,MCNN在对抗模拟真实噪声(S-R)时的实验情况,经过两轮修正(第三轮截止训练)数据集噪声率下降至设定阈值。

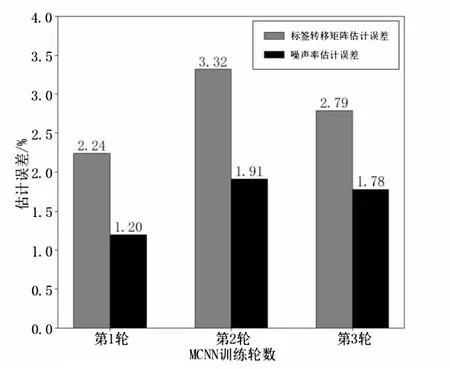
图2 MCNN对抗S-R时标签转移矩阵和噪声率的估计误差

图3 MCNN对抗S-R时的带噪数据筛选精度、修正准确率和意外改错率

3.7.2 标签转移矩阵和噪声率的估计情况

图2中结果表明,MCNN能够实现对数据集标签转移矩阵的准确估计,在两轮修正过程中标签转移矩阵的估计误差波动在2.24%～3.32%之间。同样地,MCNN提出的加权平均噪声率可以较准确地估计数据集的噪声率,由图2可以看出在3轮训练过程中估计误差波动在1.20%～1.91%之间。

3.7.3 筛选带噪数据和修正情况

MCNN在处理模拟真实噪声(S-R)时的筛选带噪数据和标签修正情况如图3所示。由图中数据可得:在筛选带噪数据上MCNN表现良好,带噪数据筛选精度波动在81.64%左右;在噪声标签修正方面,可以看出MCNN虽无法实现对筛选出的全部的噪声标签进行正确修正,但是在两次修正过程中修正准确率均远大于意外改错率,即MCNN在各轮训练上均可实现对标签的“正向修正”。

综上所述,提出的网络框架MCNN能够实现数据集质量提升的两个关键方面,因此在经过多轮修正后数据集质量水平可达到预期目标,训练所得分类网络能够实现较理想的分类性能。

4 结束语

提出了一种通用的基于多轮修正的抗噪声标签神经网络框架MCNN,以解决分类任务中噪声标签对网络性能的影响。MCNN首先基于神经网络的学习特性将带噪声标签数据按噪声率比例筛选出来,之后利用修正方案修正噪声标签逐轮提高数据集质量,最后利用高质量的数据集训练网络。在多个真实数据集和多种噪声类型下与其他基准方案进行了比较,结果表明提出的MCNN有较好的抗噪声标签能力。利用多轮修正的方法对数据集中的噪声标签进行尽可能的修正,然而对于筛选出的带噪数据可能不必要全部进行修正,转而利用选择策略[21]选取其中对网络参数有显著影响的样本进行修正,则可优化多轮修正的轮数和代价。之后的工作将是发掘、设计一些可行的选择策略来选取数据,这是文中工作的一个后续展望。