基于卷积注意力和对比学习的多视图聚类

倪团雄,洪智勇,余文华,张 昕

(1.五邑大学 智能制造学部,广东 江门 529020;2.粤港澳工业大数据协同创新中心,广东 江门 529020)

0 引 言

随着信息社会的发展,数据的表示形式更加丰富,单一数据形式往往难以充分表达数据的完整信息,而多视图数据可以弥补样本特征单一的缺点,更加全面地表征数据。多视图数据是指从同一数据源提取的不同特征集或者多个来源的数据[1]。例如,传感器信号的时域和频域特征、图像的颜色和纹理等特征、三维物体不同角度的成像特征等等。然而,实际应用中很难获取经过有效标注的数据样本,而无监督学习只需要关注数据本身,数据之间的映射关系存在很大的研究空间。聚类作为无监督学习重要的算法之一,可解释较强,学习参数少,因此无监督的多视图聚类学习吸引了学者们的广泛关注。多视图聚类根据数据本身的特征,综合不同视图的互补信息,通过学习共识函数,将具有相似结构的数据划分到不同的类簇中,已经在数据分析[2]、生物信息[3]、自然语言处理[4]、社交网络[5]等领域得到关注和应用。因此,多视图聚类学习具有重要的研究意义和应用场景。

现有的多视图聚类方法主要分为两类:传统机器学习方法和深度学习方法。在传统算法中,一些机器学习方法[6-7]将特征表示和聚类过程互相分离,这种方式不利于后续的聚类优化。为了改进这种缺陷,基于子空间学习的方法[8-14]假设所有的视图数据共享一个潜在的公共子空间,通过探索多视图的互补信息将多视图数据投影得到共同的低维映射。如Zhang等[12]直接通过多视图学习子空间表示,分别沿着交替方向最小化和广义拉格朗日乘子优化模型,使得每个视图的信息更加互补。基于协同训练的聚类算法[15-16]则根据先验知识充分地学习促进不同视图的信息,达到最大限度的共识聚类。如Kumar等[5]较先提出具有协同训练思维的多视图谱聚类,比如成对共正则谱聚类。算法假设一对数据点之间的关系在所有视图中保持一致的类簇,使得两个点在所有视图内要么都出现在同一簇中,要么都属于不同的簇。受到相同启发,Zhao等人[16]基于协同训练框架,提出了联合K-均值聚类和线性判别分析[17]的多视图聚类算法,利用在一个视图学习的标签引导其他视图的判别子空间。其他主流算法如基于图[18-22]和多核学习方法[23-27],它们都假设多视图数据可以用一个或多个核矩阵构成特征空间。以上这些传统方法虽然解释性较强,但受限于浅层和线性的学习函数,难以表达数据特征的深层信息,从而影响聚类效果。基于深度学习方法的聚类工作原理与上述方法类似,只是表征学习采用深度神经网络。例如,基于深度图学习的方法[28-31]使用图神经网络结合亲和度矩阵对多视图数据进行聚类。类似地,深度子空间方法[32-33]与上述都有相同的子空间假设,但需要计算深度神经网络中间表示的自表示矩阵。另外,对抗性方法[34-35]通过生成器和判别器对齐不同视图中隐藏特征表示的分布。如Li等[34]通过深度自动编码器学习各个视图共享的潜在表示,同时利用对抗训练来进一步捕获数据分布和分解潜在的空间。这些深度模型虽然能学习到视图的深层信息,但卷积运算主要作用在图像的局部近邻上,往往会丢失全局的关键信息,难以合理分配特定视图的权重。

针对这些问题,笔者认为,基于深度学习的多视图聚类方法关键在于如何提取关键的视图信息及如何融合不同视图特征从而引导聚类过程。受卷积注意力算法[36]的启发,该文提出一种基于卷积注意力和对比学习的深度多视图聚类网络(AEMC)。主要贡献在于:首先,该模型结合卷积层和卷积注意力模块,构造编码器网络,通过两个维度的注意力模块,提取每个视图的高层次细节特征,其次,为了引导聚类的优化方向,使用对比学习策略,通过构造正负样本间接引导模型的聚类效果。

1 基于卷积注意力的深度多视图聚类

1.1 卷积注意力模块

卷积注意力模块(CBAM)[36]是一种沿着两个维度(通道和空间)计算注意力图的深度网络模块。假设给定一个特征图F,CBAM模块将依次通过通道和空间注意模块,分别在两个维度上学习关键信息和位置,然后将注意力权重和特征图相乘,输出特征图的维度保持不变。卷积注意力模块的具体结构如图1,具体实现步骤如下:

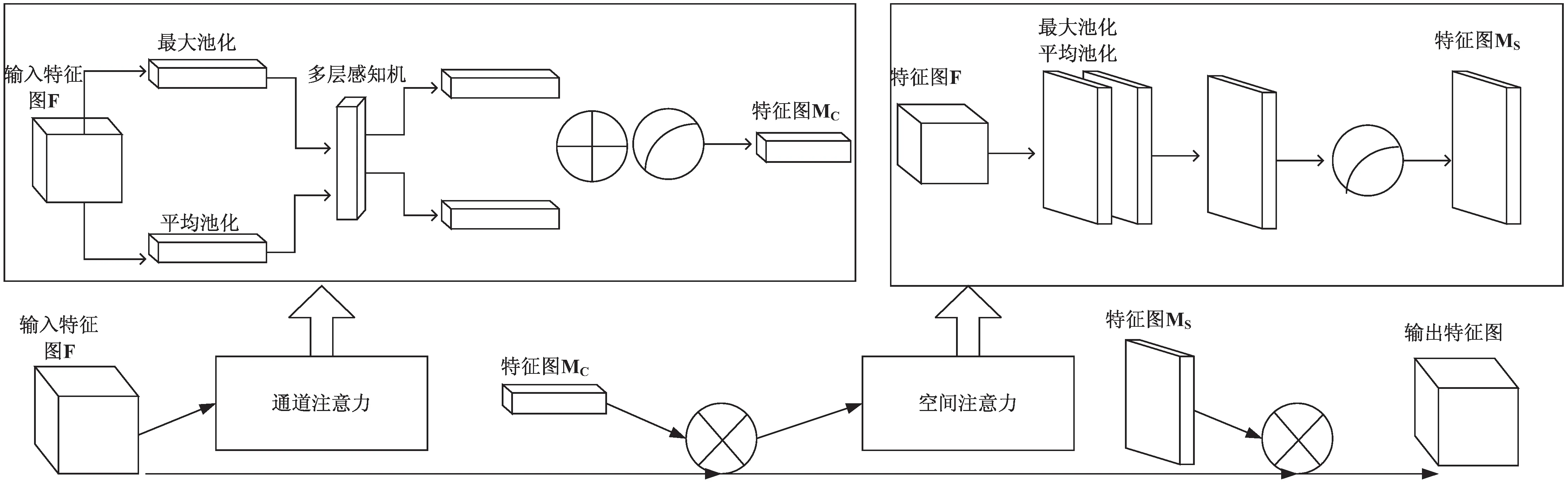
图1 卷积注意力模块

Mc(F)=σ(MLP(AvgPool(F))+

MLP(MaxPool(F)))=

(1)

其中,σ、φ0、φ1分别是激活函数和多层感知器的参数。

Ms(F)=σ(f(7×7)([AvgPool(F');

MaxPool(F')]))=

(2)

将该模块融入设计的深度多视图聚类模型中,通过提取通道和空间多维度的特征信息,平衡全局和局部注意力特征,从而影响后续的多视图聚类效果。

1.2 模型结构

假设给定样本总数为n的多视图数据集

图2 聚类模型(主要由编码器模块和聚类模块组成:编码器用于提取视图的关键信息,聚类模块通过对比方法和深度发散聚类引导聚类过程)

(1)编码器网络e(i)。在编码器模型结构中,将卷积注意力模块分别嵌入3层卷积神经网络中,构成编码器网络,每一层的结构如图3,其中卷积层采用3×3的卷积核,激活函数使用Relu ,池化层选择窗口为2×2,步长为2的最大池化。

图3 编码器结构

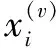
(3)

接着,将不同视图的特征进行融合,得到公共表示zi:

(4)

其中,wi是初始化视图的权重。

最后,将公共表示zi通过带softmax激活函数的全连接层进行降维,从而得到k维的输出向量ai。

1.3 损失函数

损失函数用于衡量模型的预测值和真实值的差异程度。该文选择基于深度发散的聚类(DDC)[37]损失作为基准聚类损失,该聚类损失由三部分组成:多密度泛化的柯西—施瓦茨发散项,其公式为:

(5)

其中,k表示聚类簇的数量,kab为高斯核函数,表示为:

(6)

其中,θ是超参数。

第二项为不同数据样本之间的正交聚类分配:

(7)

最后一项则将聚类分配向量逼近标准单纯形:

(8)

其中,mbj=exp(-‖ab-ej‖2),总的聚类损失Lc由式(5)(7)(8)组成,即 :

Lc=L1+L2+L3

(9)

然而聚类过程还缺乏一定的引导方向,同时为避免模型过拟合以及优化模型,该文在聚类损失中融入对比损失函数,共同优化总的损失函数。受对比学习方法SimClr[38]的启发,将其重构并融入模型的聚类模块中。文中模型将SimClr的损失函数重构表示如下:

(10)

其中,exp()函数表示以自然数e为底的指数函数,p()采用1层隐藏层的多层感知器,将其映射到对比空间,sim()表示余弦相似度,τ为温度超参数。在该模型中,选择经过dropout[39]数据增强后的视图样本和融合后的样本作为正样本,其他的样本作为负样本,对比损失目标在于增加正样本间的相似度,减少和负样本的相似度。因此,最后模型总的优化损失函数L表示为:

L=Lc+ρLs

(11)

其中,ρ为对比损失参数。

2 实 验

2.1 数据集

在四组公共多视图数据集上评估所提出的模型(AEMC),并将其与其他主流模型进行比较。四个数据集分别是:

(1)E-MNIST:E-MNIST是一组公共基准数据集,由28×28像素的60 000个手写数字图像(10个类别)组成。在实验中使用由文献[26]提供的版本(包含60 000个样本),包含原始的灰色图像视图和数字边缘视图。

(2)E-FMNIST:这是手写数据集MNIST的另一个版本,数据视图同样包括原始数字和边缘检测双视图。

(3)PASCAL VOC2007(VOC):采用由文献[40]提供的数据集,总共20种类别,数据集包含人工标注的自然图像GIST特征和词频计数特征。

(4)SentencesNYU v2(RGB-D),由1 449张经过标注的室内场景的图像以及它们的相关描述信息组成。具体如表1所示。

表1 数据集概述

2.2 实验设置

实验系统环境为Red Hat 4.8.5,硬件环境:GPU为16 GB显存的NVIDIA Quadro P500,CPU为Intel Xeon的GOLD 5118处理器,软件环境:cuda10.02和python3.7,采用Pytorch深度学习框架搭建模型。

在公开的基准数据集上验证模型的效果,主要的超参数设置如下:实验的训练批次epoch设置为100,使用默认参数的ADAM优化器优化模型,CBAM模块使用文献[31]中的默认参数,超参数θ设置为0.2,多视图权重wi初始化为均值0.5,温度超参数τ采用文献[33]推荐的τ=0.1,学习率lr设置为0.01,对比损失参数ρ设置为0.05。为了降低实验结果的随机性干扰,在每组数据集重复训练5次并取其平均值作为实验评估结果。并和当前几种经典深度模型进行对比,同时,将深度发散聚类模型(DDC)作为独立参考模型,并通过消融实验对模型的组成部分进行分析对比。

评估指标:

为更精准地评价聚类算法,采用聚类准确率(ACC)和标准互信息(NMI)来评价深度聚类算法的性能。其中ACC表示正确聚类的样本占总样本的比例,NMI则是基于信息论思想,用于度量两组样本之间的相似度,两组评价指标的值越大代表聚类效果越好。假设y和y'分别表示模型的聚类标签和数据集的真实标签,ACC计算公式如下:

(12)

假设n个数据样本聚类得到的类别C=c1,c2,…,ck,真实聚类为L=l1,l2,…,lj,NMI表达式为:

(13)

其中,I(l,c)=H(l)-H(l|c)表示互信息,H(X)为信息熵。

2.3 对比模型

为了评估模型的性能,将提出的基于卷积注意力编码器的多视图聚类模型(AEMC)同当前主流的多视图聚类模型进行对比,对比模型包括:

(1)深度多模态子空间聚类(DMSC)[32];

(2)基于端到端对抗性注意力网络的多模态聚类(EAMC)[35];

(3)深度典型相关性分析(DCCA)[41];

(4)深度对抗多视图聚类(DAMC)[34];

(5)对比多视图聚类(CoMVC)[42]。

另外,为了检验改进后的模型整体结构相对基准聚类是否提高聚类效果,从而证明模型的卷积注意力编码器模型和对比学习策略的优势,将基准深度发散聚类模型(DDC)作为独立对比组。

2.4 结果与分析

2.4.1 模型对比结果分析

定量研究了E-MNIST、E-FMNIST、VOC、RGB-D四组数据集在卷积注意力编码器模型上的表现,结果见表2。从表中对比结果可知,文中模型在手写数据集E-MNIST和E-FMNIST上的聚类准确率,标准互信息优于大多数模型,聚类准确率分别领先文献[42]中的对比聚类方法(CoMVC)0.7百分点和1.3百分点,在E-MNIST上的标准互信息高于对比聚类方法(CoMVC)1.2百分点;在VOC和RGB-D数据集上则优于大多数主流模型,但略低于对比聚类方法。

表2 不同数据集上不同模型的对比结果 %

另外,在独立对比实验中,进一步探索了模型(AEMC)和深度发散聚类基准模型(DDC)在4组数据集上的聚类效果,具体见表3。从表中数据可知,该模型在4组数据集上较深度发散基准模型都有明显的改善,特别是在E-MNIST公共数据集上,聚类准确率和标准互信息分别提高了10.2百分点和8.1百分点。

表3 不同数据集上AEMC和DDC模型的对比结果 %

综合以上分析,将卷积注意力模块嵌入编码器网络中以及聚类优化中使用对比学习策略,能够提取视图的更多关键特征,引导模型的聚类方向,从而提高聚类效果。聚类结果表明,多视图融合表征的质量有助于对比学习策略的使用,两者又相互促进聚类的效果。因此说明该模型具备一定的有效性和鲁棒性。

2.4.2 损失函数研究

为更直观地观察基准损失和模型损失函数的变化,以数据集VOC为例,将数据集的基准聚类损失和总的损失函数进行可视化。模型在训练过程中Loss曲线随迭代批次epoch的变化如图4所示,其中,依次选择每10次迭代的Loss值构成散点。从图中曲线变化得知,模型经100次训练后逐渐收敛,基准模型和文中模型在训练100批次后损失函数也趋于稳定,因此epoch的设置合理,模型训练足够充分。

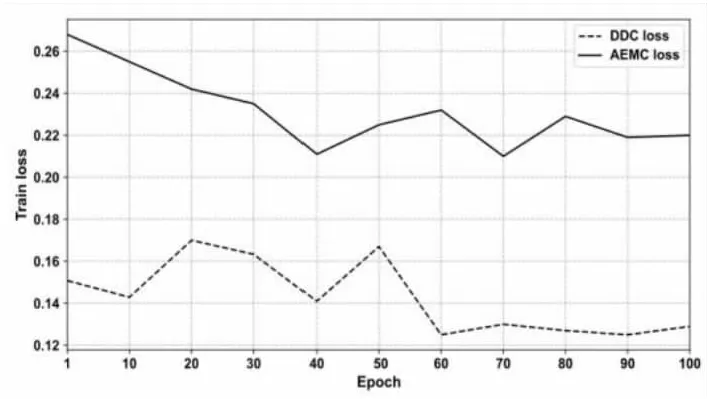
图4 模型Loss变化曲线

2.4.3 消融实验

前面的实验初步证明模型具有一定的效果,然而模型的具体结构对聚类结果的影响程度还不清楚。因此,为了进一步探索模型具体结构的实际聚类效果,对模型不同结构组合的聚类结果进行消融对比实验。如表4,实验分别设置无CBAM和正负对比样本,有CBAM模块但无正负对比样本,无CBAM模块但有正负对比样本三组对比参照组。

表4 在E-MNIST,VOC数据集上的消融结果 %

从表中结果可以发现,当模型缺少卷积注意力模块(CBAM)和对比损失优化函数Ls后,该模型在E-MNIST,VOC数据集上的聚类精度分别下降了6.5百分点、7百分点,同理,无卷积注意力模块(CBAM)和对比损失优化函数Ls,标准互信息值分别下降了1.7百分点和12.6百分点,由此可知卷积注意力模块和对比策略相对模型有所改进。

此外,以E-MNIST数据集为例,分别可视化其在训练过程中文中模型和深度发散基准模型的曲线变化结果,如图5所示。其中图5(a)是E-MNIST数据集训练聚类精度随训练迭代次数的变化曲线,模型的精度随着训练次数增加逐渐收敛,并在95%附近趋于稳定,且精度高于基准聚类模型。同理,图5(b)为E-MNIST数据集标准互信息随训练批次的变化曲线,在92%附近逐渐平缓,同样高于基准聚类模型。因此,消融实验表明模型的卷积模块和对比学习模块促进聚类的效率,提高了聚类的准确率和标准互信息值。

(a)聚类精度

3 结束语

针对传统多视图聚类算法浅层学习的限制和深度学习方法多维度特征学习的局限问题,提出一种基于卷积注意力机制的深度多视图聚类网络,将卷积注意力模块结合卷积模块构成编码器网络,提取每个视图的通道和空间关键特征,提高多维度特征的关注度。此外,在优化聚类模型时使用对比学习策略,防止过拟合及引导模型的聚类方向。实验结果表明,模型的聚类准确率较高,聚类效果明显。

然而,该研究也存在诸多不足,比如数据集形式单一、模型训练参数较多、训练内存和时间消耗大等等。未来的研究将会关注复杂的多视图数据及网络改进,如图像和文本数据的结合,数据缺失的多视图数据的处理,以及预训练网络,探索更多类型的数据集是否有利于注意力参数的优化和网络的兼容性。