改进HS算法在码垛机器人轨迹规划中的应用

崔迎超，汪志锋，徐洁，任明

改进HS算法在码垛机器人轨迹规划中的应用

崔迎超，汪志锋，徐洁，任明

（上海第二工业大学，上海 201209）

解决码垛机器人在抓取目标物时需要满足最大速度约束条件、较短运行时间以及运行平稳性等问题。以Func200id六轴工业机器人为研究对象，通过机器人的各关节尺寸关系计算其DH参数，并建立仿真模型。对改进的HS算法通过增加变异因子VF来改变算法的搜索策略，使得算法中的每个个体不但有机会参与到迭代的过程之中，而且有概率向最优个体学习，加快算法的收敛速度。通过对4种算法在6种不同测试函数下分别运行30次的对比实验可知，改进后的HS算法相较于其他3种算法的寻优能力更强，收敛速度更快。改进后的HS算法能够明显缩短码垛机器人的工作时间，且运行连续平稳，在其他工业场景下也具有一定的应用价值。

码垛机器人；轨迹规划；HS算法；时间优化；3-5-3多项式插值

在工业生产过程中，码垛机器人的自动化、高效化的优点已逐渐替换传统的人力操作。码垛型关节式机器人由于其具有结构简单、操作精度高以及工作场景适应性强的特点，已广泛应用在产品包装、设备制造、仓库储存等众多场景中[1]。在对机器人运动规划过程中，研究其时间优化方法，对提高工业制造过程中的生产效率具有显著意义。

在机械臂轨迹规划中，根据规划的位置不同，分为笛卡尔空间规划和关节空间规划2种类型。由于笛卡尔空间规划针对机器人末端执行器，需要对位姿实时逆向求解，计算量庞大，且存在机械臂奇异的现象[2]，所以本文采用关节空间规划进行实验研究。

在拟合机械臂运动曲线的方法中，多项式插值算法计算简单，使用范围最广，但是单一的多项式函数不能区分分段点的速度或加速度[3]。B样条插值算法虽然具有局部性和连续性的特点，但是无法保证运动曲线的光滑性[4]。样条插值算法是将运动曲线分为若干段，每段的运动曲线都使用多项式进行拟合。由于多项式系数是在分段点前后相同状态下得出，故而能够保证分段点处各分段的连续性和平滑性。徐鹏飞等[5]使用4-3-4分段多项式对工业码垛机器人进行轨迹规划，提高了码放货物过程的流畅性、稳定性和连续性。郭鑫鑫等[2]使用3-5-3分段多项式对改进的萤火虫算法进行优化轨迹设计，缩短了机械臂的运行时间。

启发式算法通常是模拟现实世界的物理规则，因其结构简单的特点，已广泛应用于工业机器人。Wang等[6]利用改进鲸鱼优化算法，杨星涛等[7]使用改进遗传算法进行最优时间计算。为解决蚁群算法的不确定搜索、搜索效率较低的问题，魏立新等[8]提出了将蚁群算法与DWA算法相结合的融合算法。米根锁等[9]通过改变步长因子来提高布谷鸟算法寻优效率，使工业机器人具有更好的鲁棒性。

1 关节空间规划问题

1.1 3-5-3多项式插值函数

在机械臂轨迹规划过程中，若使用单一的多项式插值函数，会使得机械臂在运行过程中，某些路径点会出现速度和加速度突然变化的现象。若使用单一的高次多项式，随着次数的增加，除了计算成本的提高，插值的过程中还会引起“龙格现象”，影响机械臂运行的稳定性和使用寿命。采用分段低次插值的思想，不仅可以避免插值曲线突变的现象，也可以在满足计算要求的情况下，获得高次插值的效果。本文采用3-5-3多项式插值函数来拟合曲线，该多项式第1段为三次多项式，第2段为五次多项式，第3段为三次多项式。具体公式见式（1）—（3）。

第1段曲线：

第2段曲线：

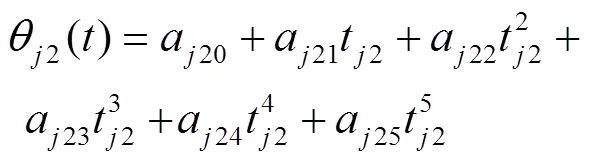
第3段曲线：

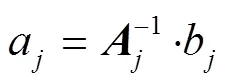
其中：

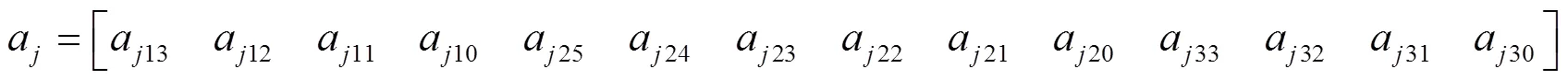
1.2 优化目标函数的选取

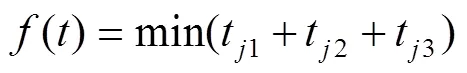
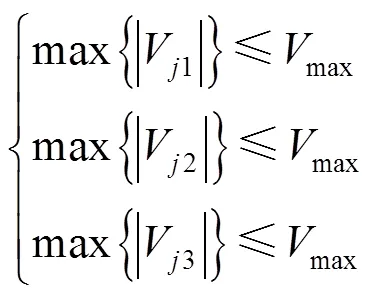
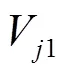
2 改进HS算法后的轨迹规划

2.1 HS算法的基本思想

韩国学者Geem等[11]于2001年根据音乐剧场中乐师不断调节手中乐器的音调来实现优美的和声提出了HS算法。该算法将不同乐器的音调作为变量，改变变量的过程来模拟乐师利用经验来调节音调的过程，最终使乐曲达到完美和声状态来找到最优解[12]。HS算法相较于其他传统的启发式优化算法，其操作简单、参数较少、易实现寻优策略等优点被大量应用在多目标求解的应用场景[13]。

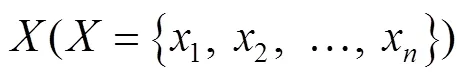
2.2 改进的HS算法

在标准的HS算法中，每次即兴创作只是修改群体中某个个体的信息，忽略了其他个体对群体的影响，尤其是较差的和声个体，因此算法在迭代过程中极其依赖初始库中最优和声代表。文献[14]中提出将适应度低的和声与适应度高的和声在对称区间内生成新和声的方法。虽然可以使和声能够更快地向好的和声收敛，但是求解结果容易产生局部最优值。

为了增加其他和声与最优和声的关联度，提高算法的全局搜索能力。改进HS算法采用每个和声都有机会参与迭代的策略，增加变异因子VF（Variation Factor）。参数VF用来判断是否对和声进行修改，VF值较高时有利于加快算法的收敛速度，但是会增加程序的运行时间；VF值较低时虽然会提高和声修改的轮空次数，但是不利于算法的快速收缩。

基本和声算法中参数HMCR用来判断被选中的和声是扰动调节还是整体修改，在改进HS算法中HMCR被用来区分和声修改范围的大小，即一部分用于和声整体修改的策略，可增加全局搜索的概率。一部分用于和声中单个变量的修改，提高收敛速度。整体修改策略下新生成的和声变量见式（10）。

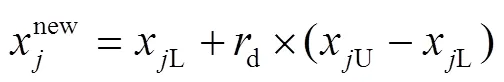
当HMCR值设置较小时，单个和声从解析空间中随机生成新的和声概率提高，虽然有利于避免局部最优解的现象发生，但是不利于提高算法的运行时间。当设置的值较大时，最优解可以在已有的和声搜索库中迅速收敛，但是可能会陷入局部最优。

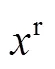
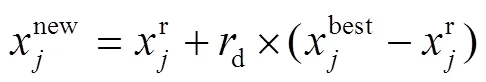
新变量扰动调节公式见式（12）。

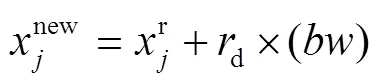
参数PAR值的更改使得所有和声都有机会向最优和声学习，能够提高算法的收敛能力。但是如果PAR值设置得较大，会提高求得局部最优的风险。如果值设置的较小，单个和声变量只能以带宽（BW）的步长向最优解移动，会增加算法的迭代次数。

改进的HS算法的操作步骤如下：

1）初始化参数。设置和声记忆库大小（HMS）、最大迭代次数max、变异因子（VF）、和声记忆库取值范围概率（HMCR）、音调微调方式概率（PAR）以及音调微调带宽（BW）。

2）初始化种群HM。在可行域内生成初始种群HM，其矩阵见式（13）。

3）即兴创作产生新和声，伪代码如下所示：

for j=1:Tmax %即兴创作开始

if rand < VF %对和声记忆库进行操作

if rand < HMCR %区分是否整体调节

if rand < PAR %选择调节方式

xjnew= xjr+ rand×(xjbest–xjr)

end if

xjnew=xjr± rand × bw %扰动调节

end if

xjnew=xjL+ rand×(xjU–xjL)

end if

end for

改进HS算法的流程如图1所示。

图1 改进HS算法流程

图1中自生成随机数0开始到是否满足停止条件为止，为步骤3即兴创作产生新和声的迭代过程。其中0、1和2均为随机数，分别与VF值、HMCR值和PAR值进行比较，用来更新和声库。当生成一组新的和声成员后，将该和声成员的优化目标函数值与现有和声库中最差成员进行对比，若优于最差成员，将其替换，若弱于最差成员，则原有和声库不变。

3 仿真模型的建立

3.1 模型的建立

表1 Func200id机器人D-H参数

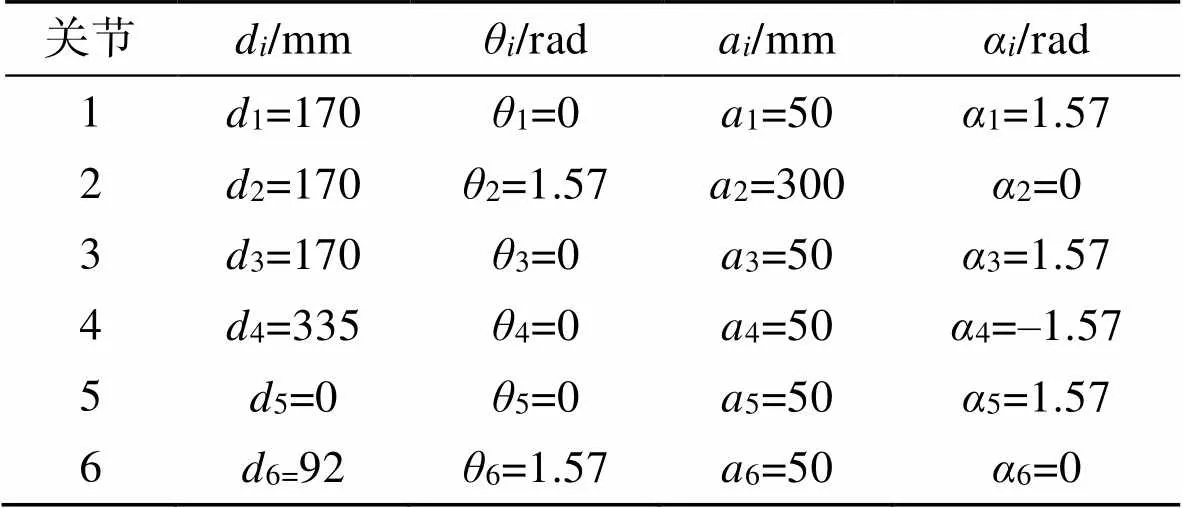
Tab.1 D-H parameters of Func200id robot

表2 各关节约束

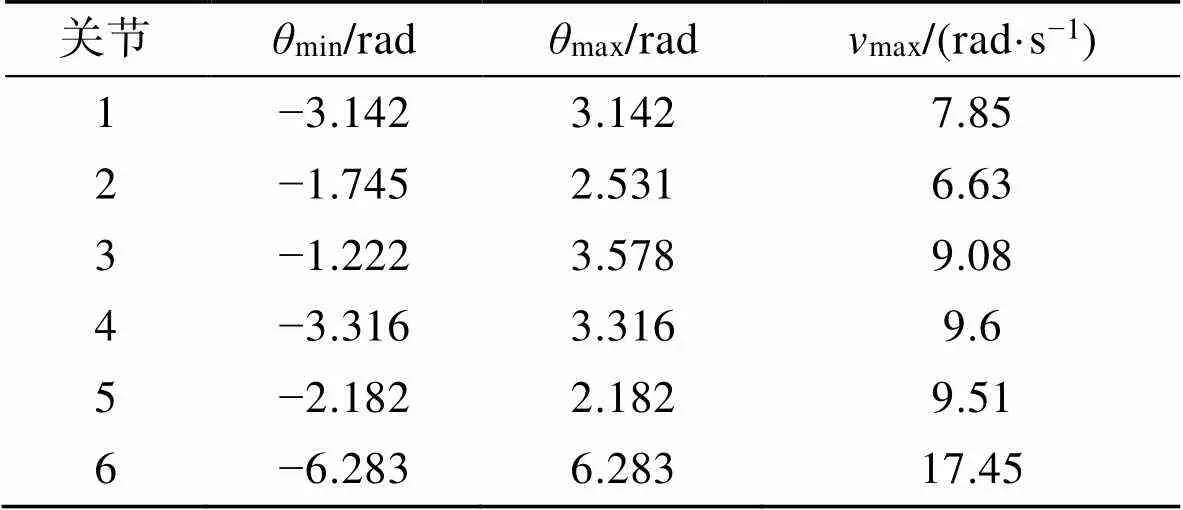
Tab.2 Each joint constraint

表3 各关节运行路径插值点

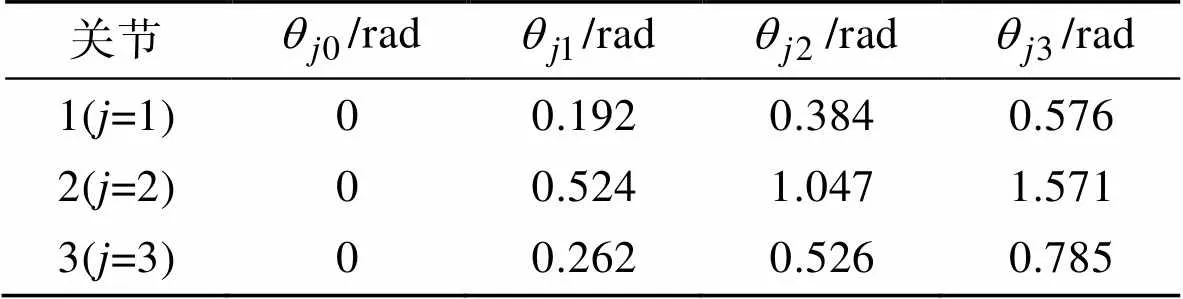
Tab.3 Interpolation points for each joint running path

根据上述条件，在Matlab中构建机器人运动模型。设置改进HS算法的初始个体数HMS值为5，乐器数量为3，创作的次数max为200，HMCR值设置为0.95，PAR值为0.7，BW值为0.2，max范围为[3, 3, 3]，min范围为[0, 0, 0]。

3.2 VF值选取

由于VF值决定了程序的运行速度和函数的收敛速度，合适的VF值设定有助于系统更快地求解合适时间。考虑到计算机的配置、运行环境以及随机数生成的随机性等因素，本文对不同VF值分别进行了10次求解的对比性实验，其参数设置参考3.1节，对VF值求平均值，结果如表4所示。

表4 不同VF值求解结果平均值

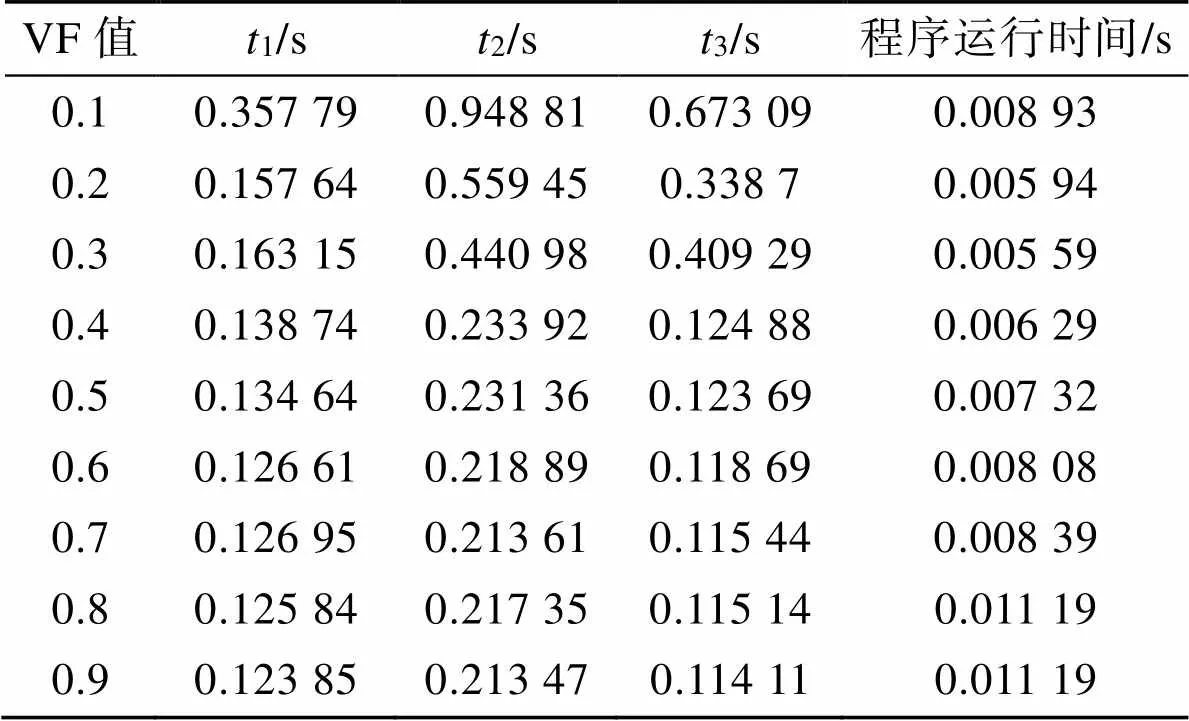
Tab.4 Average solution results of different VF values

表4中，从整体来看，当VF取值增大时，程序的运行时间也会增加。当VF取值为0.1～0.5时，其程序的运行时间虽然较短，但所求解的变量并不是最优解。当VF值取0.8和0.9时程序的运行时间高于VF值取0.6和0.7时程序的运行时间，但所求解的变量值并非最优解。从求解结果来看，VF值取0.7是优于0.6的，故本文中VF值确定为0.7。

4 仿真结果与分析

4.1 改进HS算法仿真结果分析

为验证改进HS算法的鲁棒性和有效性，本文将HS、IHS、改进GA[7]等3种算法在约束函数（式（8）—（9））和5种经典测试函数下优化求解。表5中给出了5个经典测试函数的表达式、搜索范围、维度和最优值。其中F1和F2为单峰函数，F3和F4为多峰函数，F5函数为二维的定维函数。

表5 5种经典测试函数

Tab.5 Five classic test functions

5个经典测试函数对应的参数设置如表6所示。其中算法搜索范围和变量数量参考表5，迭代次数统一设定200次，运行环境为Matlab2020a。

表6 4种算法参数设置

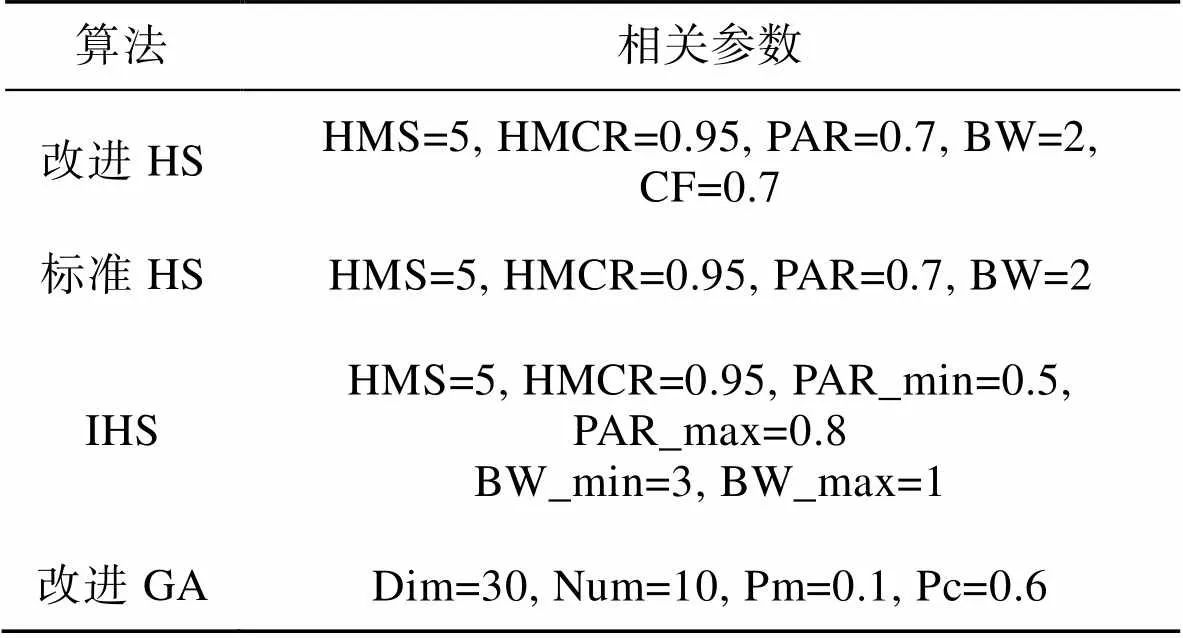
Tab.6 Parameter setting of four algorithms

在6个不同函数情况下，4种算法的寻优曲线对比见图2—7，其求解结果精度越高，曲线收敛速度越快，表示该算法的性能越好。

图2为4种算法在本文机械臂时间优化轨迹规划过程中的优化曲线。图3—7为表5所对应的测试函数优化曲线。从图2—7中可以看出，改进HS算法相较于其他2种HS算法，具有更优秀的全局寻优能力和更快的收敛速度；相较于改进GA算法，虽然改进GA算法的收敛速度更快，但是其求解结果常在最优值附近徘徊，精度难以保证。在较大的目标值时，如图3和图4所示，改进的HS算法和改进GA算法的性能明显优于其他2种算法。在较小的目标值时，如图5和图7所示，4种算法都能较快地求解最优值，但是改进HS算法和改进GA算法的速度更快。

图2 式（8）—（9）的函数优化曲线

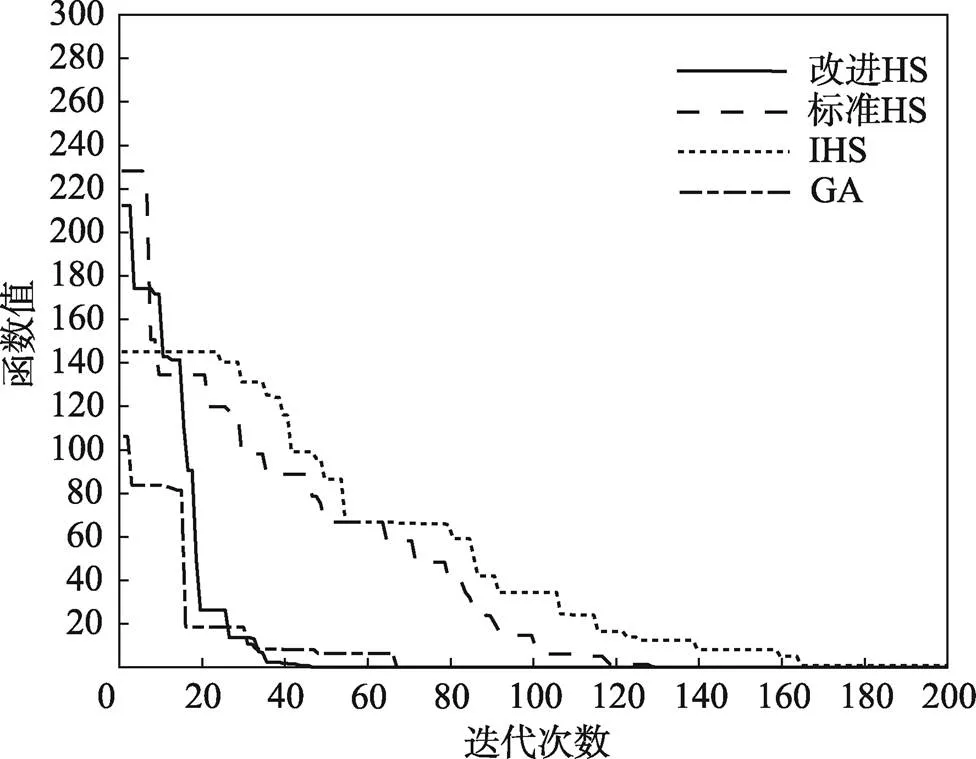
图3 F1函数优化曲线

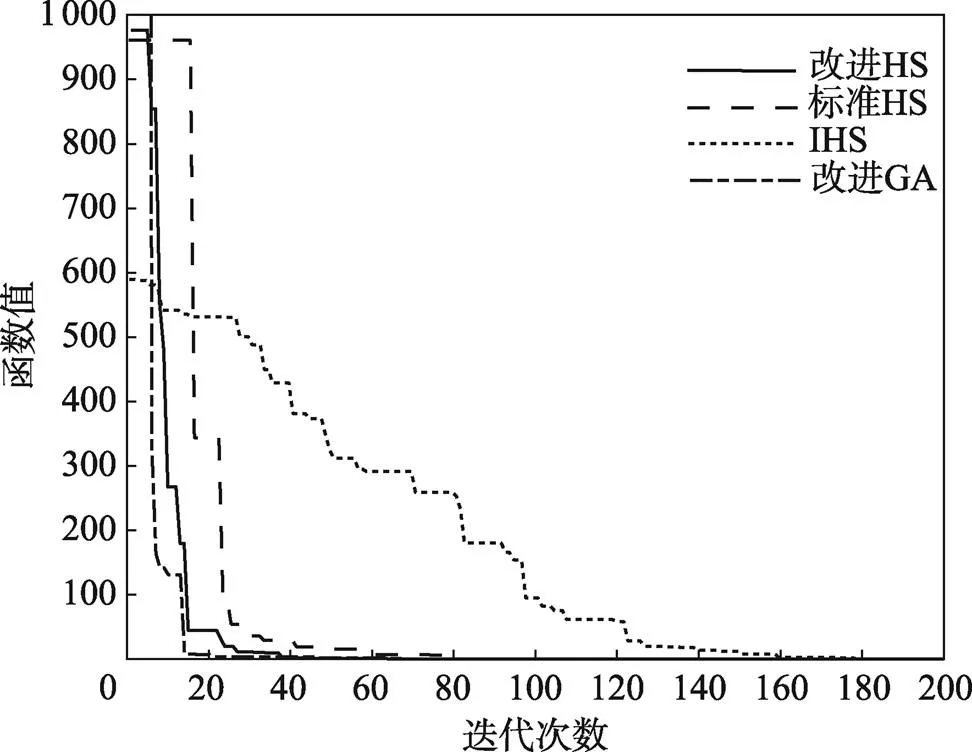
图4 F2函数优化曲线

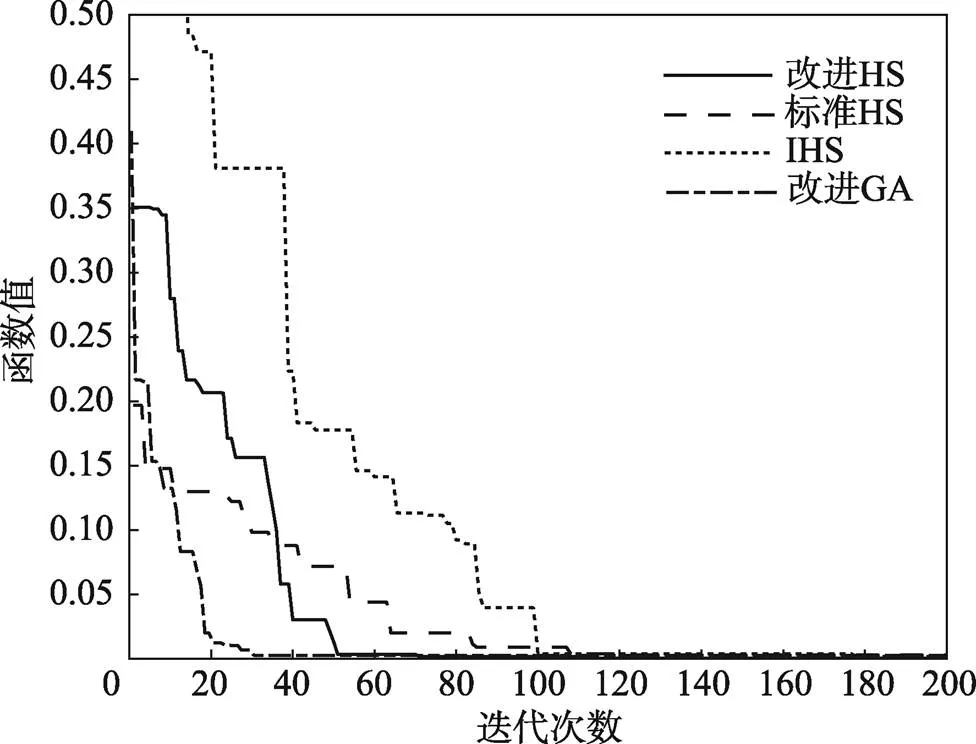
图5 F3函数优化曲线

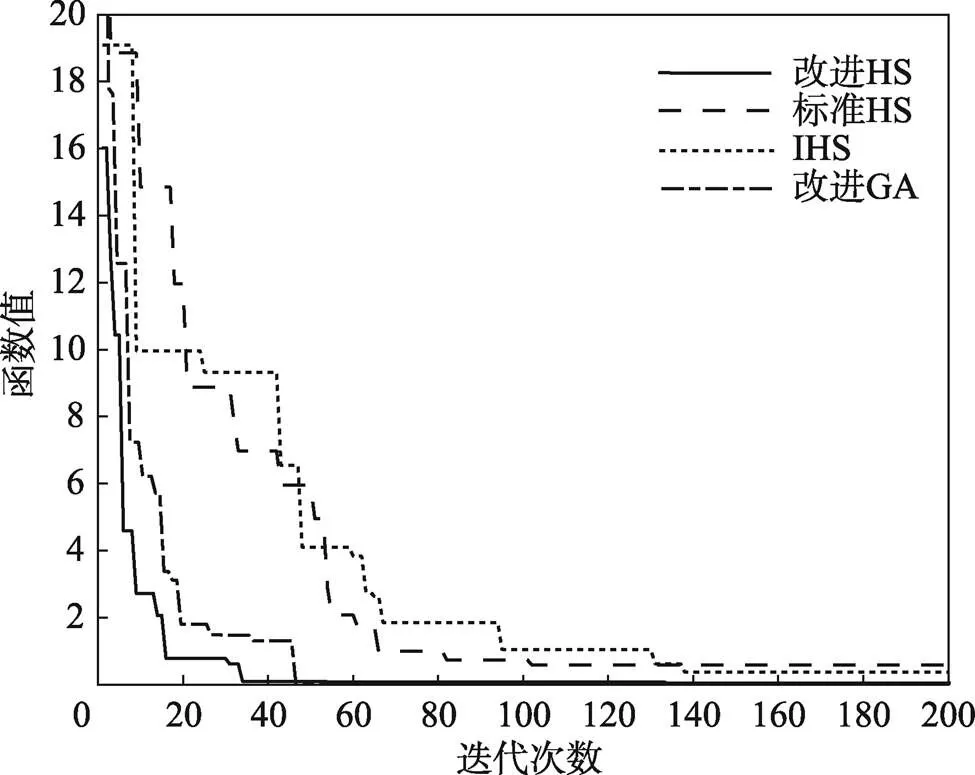
图6 F4函数优化曲线

为更好地理解实验数据、更准确地对改进HS算法和改进GA算法的性能进行对比，在保持表5和表6中参数不变的条件下，对4种算法在6个函数下，分别运行30次。对比30次结果的离散程度来判断算法的稳定性，结果如表7所示。其中MEAN表示30次运行最优值的平均值，SD表示30次运行的标准差。

图7 F5函数优化曲线

从表7中可以看出，改进HS算法相较于改进GA算法，求解结果精度更高，且标准差更低，算法的稳定性优于改进GA算法。但是在维度较低的F5函数中，改进GA算法的性能明显优于改进HS算法的，表现出了更好的稳定性和收敛性。相较于其余2种HS算法，改进HS算法的性能在6个函数中都表现得更优秀，其精度值均控制在2位小数点以上，且标准差也在2位小数以上，而其余算法求解的结果离散程度较高，系统稳定性较差。从总体上来看，改进HS算法收敛速度较快，算法稳定性较高，能够提高系统的鲁棒性。

4.2 3-5-3多项式插值函数结果分析

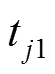
表7 4种算法运行30次结果

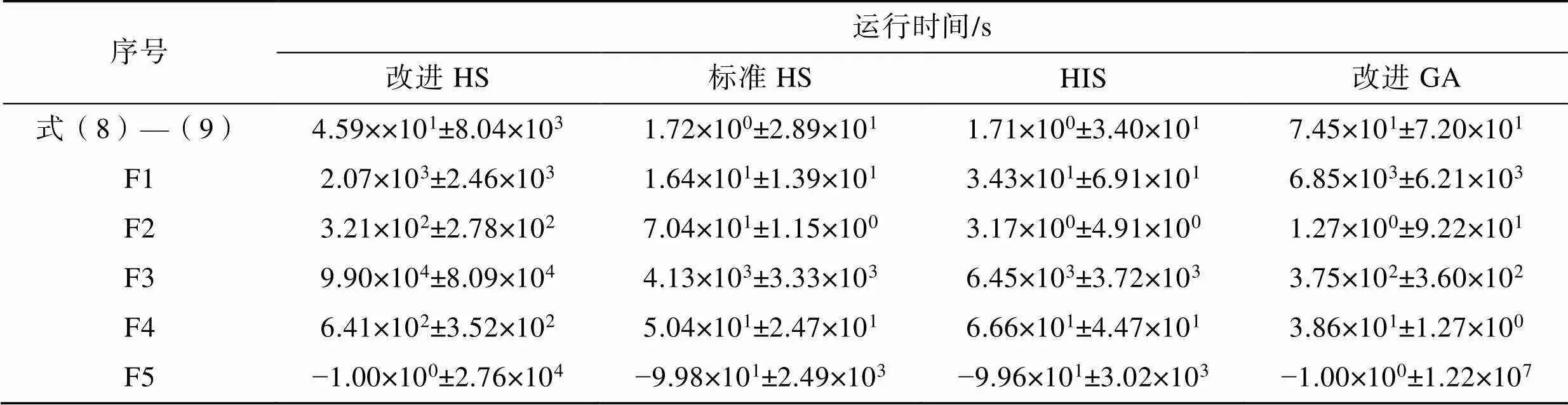
Tab.7 Results of 4 algorithms running for 30 times

注：表中数据为MEAN±SD。

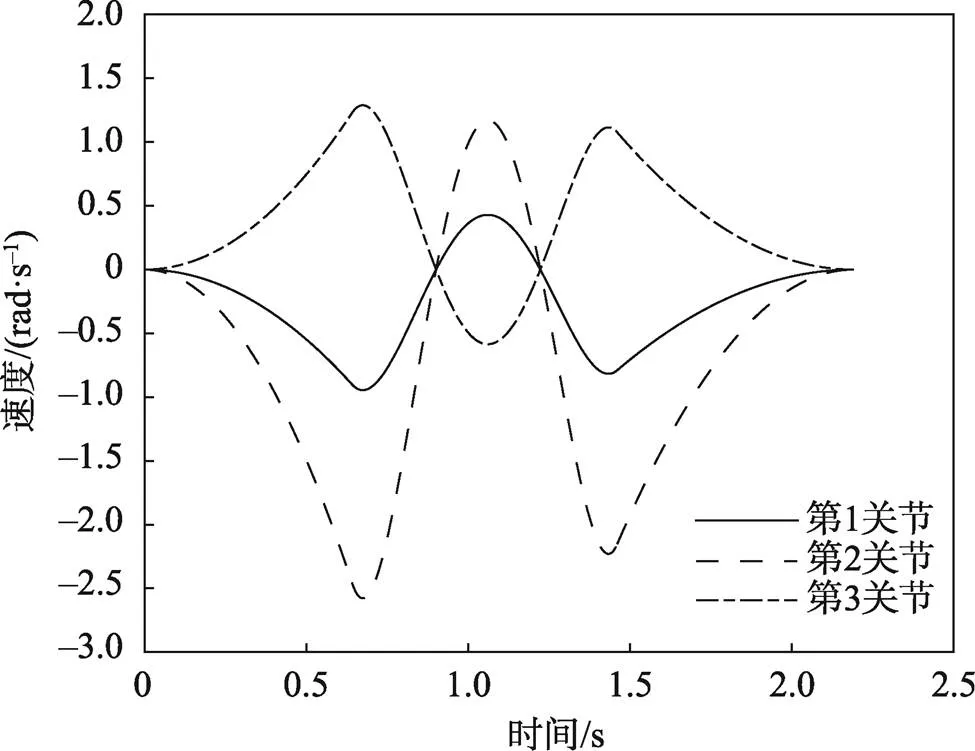
图8 未优化的3-5-3多项式插值的各关节速度曲线

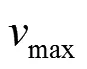
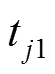
图9 改进HS算法优化后的各关节位置曲线

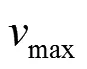
图10 改进HS算法优化后的各关节速度曲线

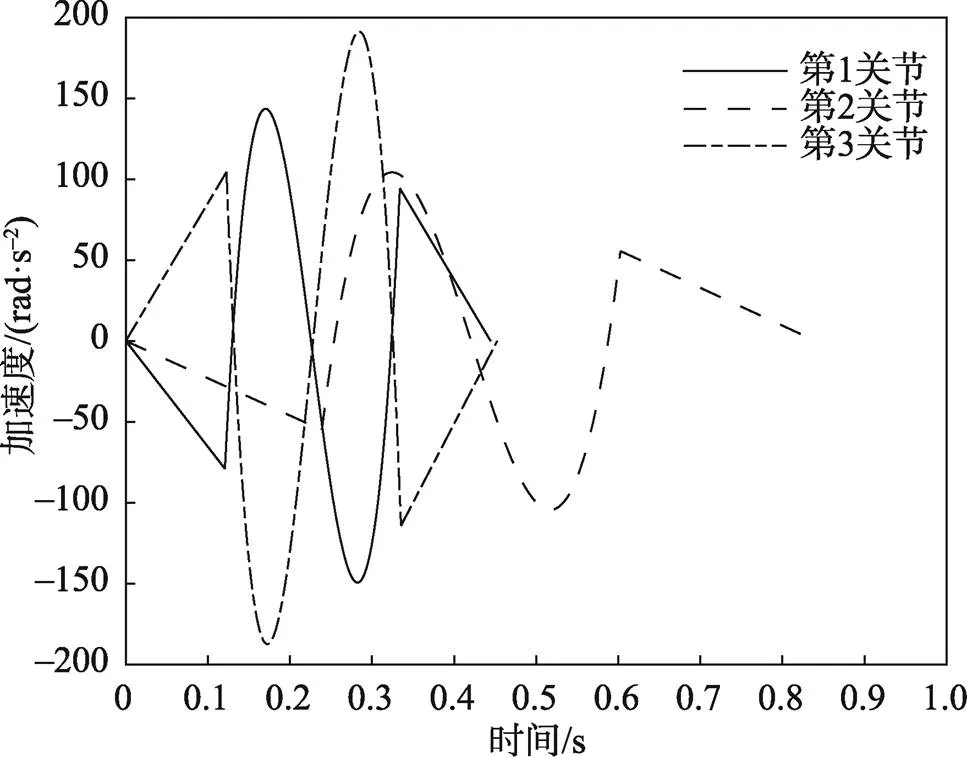
图11 改进HS算法优化后的各关节加速度曲线

5 结语

本文以Func200id机器人为研究对象，在满足机器人运动学各项约束的条件下，提出基于改进HS算法的3-5-3样条多项式插值函数的时间优化轨迹规划。通过增加变异因子VF来提高HS算法的全局搜索能力，改进HS算法的搜索策略能够在较少的迭代次数中更快地收敛，从而获得最优解。经过对照试验，改进HS算法相较于标准HS算法、IHS算法和改进GA算法具有更优秀的求解效率，并且规划出来的机器人各关节位置曲线、速度曲线和加速度曲线均具有连续性和平滑性的特点，能够降低机器人的工作时间，提高机器人运行中的系统性能。在后续的规划中，除了针对时间优化的轨迹方法外，对冲击、能量或综合能力的优化设计依旧是码垛机器人轨迹规划的重点。

[1] 胡春生, 魏红星, 闫小鹏, 等. 码垛机器人的研究与应用[J]. 计算机工程与应用, 2022, 58(2): 57-77.

HU Chun-sheng, WEI Hong-xing, YAN Xiao-peng, et al. Research and Application of Palletizing Robot[J]. Computer Engineering and Applications, 2022, 58(2): 57-77.

[2] 郭鑫鑫, 薄瑞峰, 贾竣臣, 等. 基于改进萤火虫算法的机械臂时间最优轨迹规划[J]. 机械设计与研究, 2021, 37(3): 55-59.

GUO Xin-xin, BO Rui-feng, JIA Jun-chen, et al. Time Optimal Trajectory Planning of Manipulator Based on Improved Firefly Algorithm[J]. Machine Design & Research, 2021, 37(3): 55-59.

[3] YU Xiu-li, DONG Ming-shuai, YIN Wei-ming. Time- Optimal Trajectory Planning of Manipulator with Simultaneously Searching the Opti-Mal Path[J]. Computer Communications, 2022, 181: 446-453.

[4] 任重, 杨灿军, 陈鹰. 轨迹规划中的B样条插值算法[J]. 机电工程, 2001, 18(5): 38-39.

REN Zhong, YANG Can-jun, CHEN Ying. B-Spline Interpolation Algorithm in Motion Planning[J]. Mechanical & Electrical Engineering Magazine, 2001, 18(5): 38-39.

[5] 徐鹏飞, 罗庆生, 韩宝玲, 等. 新型工业码垛机器人轨迹规划研究[J]. 组合机床与自动化加工技术, 2012(5): 70-73.

XU Peng-fei, LUO Qing-sheng, HAN Bao-ling, et al.Research on Trajectory Planning of New Industrial Palletizing Robot[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2012(5): 70-73.

[6] WANG Ting, XIN Zhi-jie, MIAO Hong-bin, et al. Optimal Trajectory Planning of Grinding Robot Based on Improved Whale Optimization Algorithm[J]. Mathematical Problems in Engineering, 2020(4): 1-8.

[7] 杨星涛, 库祥臣, 赵欢乐, 等. 基于改进遗传算法的时间最优轨迹规划[J]. 制造技术与机床, 2022(3): 74-79.

YANG Xing-tao, KU Xiang-chen, ZHAO Huan-le, et al. Time-Optimal Trajectory Planning Based on Improved Genetic Algorithm[J]. Manufacturing Technology & Machine Tool, 2022(3): 74-79.

[8] 魏立新, 张钰锟, 孙浩, 等. 基于改进蚁群和DWA算法的机器人动态路径规划[J]. 控制与决策, 2022, 37(9): 2211-2216.

WEI Li-xin, ZHANG Yu-kun, SUN Hao, et al. Robot Dynamic Path Planning Based on Improved Ant Colony and DWA Algorithm[J]. Control and Decision, 2022, 37(9): 2211-2216.

[9] 米根锁, 李明. 布谷鸟搜索算法在空间机械臂轨迹规划中的应用研究[J]. 机械科学与技术, 2018, 37(12): 1805-1810.

MI Gen-suo, LI Ming. Research on the Application of Cuckoo Search in Trajectory Planning of Space Manipulator[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1805-1810.

[10] 徐向荣, 秦锋, 毕文昌. 利用样条函数规划机器人运动轨迹[J]. 华东冶金学院学报, 1996(3): 203-208.

XU Xiang-rong, QIN Feng, BI Wen-chang. Trajectory Planning of Robot Manipulators Using Spline Function[J]. Journal of East China Institute of Metallurgy, 1996(3): 203-208.

[11] GEEM Z W, KIM J H, LOGANATHAN G V. A New Heuristic Optimization Algorithm: Harmony Search[J]. simulation, Sage Publications Sage CA: Thousand Oaks, CA, 2001, 76(2): 60–68.

[12] 王丽萍, 吴月秋, 张验科, 等. 改进和声搜索算法在梯级水库群优化调度中的应用[J]. 人民长江, 2021, 52(2): 192-196.

WANG Li-ping, WU Yue-qiu, ZHANG Yan-ke, et al. Improved Harmony Search Algorithm and Its Application in Optimal Operation of Cascade Reservoir Groups[J]. Yangtze River, 2021, 52(2): 192-196.

[13] 李敬花, 闫恒山, 杨博歆, 等. 改进遗传—和声搜索算法求解海工装备制造车间调度问题[J]. 计算机集成制造系统, 2022, 28(12): 3923-3936.

LI Jing-hua, YAN Heng-shan, YANG Bo-xin, et al. Improved Genetic-Harmony Search Algorithm for Solving Workshop Scheduling Problem of Marine Equipment[J]. Computer Integrated Manufacturing Systems, 2022, 28(12): 3923-3936.

[14] AKINTAYO A, SARKAR S. A Symbolic Dynamic Filtering Approach to Unsupervised Hierarchical Feature Extraction from Time-Series Data[C]// Proceedings of the American Control Conference, 2015: 5824-5829.

[15] ABDERRAHMANE M, DJURIC A, CHEN Wen, et al. Study and Validation of Singularities for a Fanuc LR Mate 200iC Robot[C]// IEEE International Conference on Electro/Information Technology, IEEE, 2014: 432-437.

Application of Improved HS Algorithm in Trajectory Planning of Palletizing Robot

CUI Ying-chao, WANG Zhi-feng, XU Jie, RENG Ming

(Shanghai Polytechnic University, Shanghai 201209, China)

The work aims to solve the problems of maximum speed constraint, short running time, and poor operation smoothness of palletizing robots when grasping target objects. With a Func200id six-axis industrial robot as the research object, its DH parameters were calculated by the relationship of each joint size of the robot, and a simulation model was established. The improved HS algorithm changed the search strategy of the algorithm by increasing the variation factor VF so that each individual in the algorithm not only had the opportunity to participate in the iterative process but also had the chance to learn from the optimal individual, which accelerated the convergence of the algorithm. Through a comparison experiment of the four algorithms running 30 times under six different test functions, the improved HS algorithm had stronger search capability and faster convergence than the remaining three algorithms. It can significantly shorten the working hours of the palletizing robot and run continuously and smoothly, which has certain application value in other industrial scenarios as well.

palletizing robot; trajectory planning; harmony search (HS) algorithm; time optimization; 3-5-3 polynomial interpolation

TP242

A

1001-3563(2023)15-0137-09

10.19554/j.cnki.1001-3563.2023.15.018

2022–08–29

崔迎超（1994—），男，硕士生，主攻基于视觉的工业机器人。

汪志锋（1970—），男，博士，教授，主要研究方向为工业过程控制、电子与通信工程。

责任编辑：曾钰婵