考虑微推力器输出特性的引力波探测卫星分数阶PID控制

周俊杰，庞爱平，周鸿博，孟范伟，刘 辉

（1.贵州大学 电气工程学院，贵阳 550025；2.东北大学 秦皇岛分校控制工程学院，秦皇岛 066004；3.哈尔滨工业大学 能源科学与工程学院，哈尔滨 150001）

引 言

空间引力波探测对卫星平台提出了超“静稳”需求，其关键技术之一是无拖曳控制。高精度无拖曳控制指标实现前提是微牛级推力器的精稳输出。相对卫星所受空间环境的外部扰动，微牛级推力器产生的输出扰动是严重影响系统性能的“低频扰动”[1-2]，忽略推力器的无拖曳控制设计明显不符合实际，必须进行微推进系统和卫星平台无拖曳控制的“一体化”研究，从而提升引力波探测指标实现的可能[3-7]。

随着空间精密测量任务的深入研究，目前多种无拖曳控制方法已经得到了在轨验证。首颗无拖曳卫星“TRIAD I”采用的是On-off开关控制方法[8]。GP-B卫星利用PID控制方法设计了无拖曳控制器[9-10]。GOCE卫星采用了嵌入式模型控制方法EMC（Embedded Mode Control）设计无拖曳控制器，嵌入式模型是由高精度的非线性模型适当简化获得，但是仍然保留了扰动模型和不确定性。将外界扰动当作是扩张状态加以估计，使用极点配置的方法设计控制器以调节控制器带宽及其频域性能，以保证控制指标的实现[11]。LISA Pathfinder在设计无拖曳控制器时首先将卫星动态模型进行解耦处理，再将每一个解耦回路的频域性能指标转化为对闭环系统灵敏度函数的要求，然后利用H∞回路成形技术进行鲁棒控制器设计[12]。“太极一号”卫星基于EMC理论设计无拖曳控制器，通过在轨实验性能分析，验证了“太极一号”卫星无拖曳控制系统的抗干扰能力[13]。“天琴一号”卫星着眼于工程实际问题的挖掘与解决，仅采用了简单的单积分控制器，对无拖曳控制技术进行了在轨试验，实现了10–9m/s2/Hz1/2量级的无拖曳控制水平[14]。

此外，国内外众多学者采用定量反馈理论（QFT）[15-16]、LMI（Linear Matrix Inequalities）方法[17]、频率分离控制[18]、自抗扰控制[19]、最优控制[20]、自适应变域模糊PID[21]等诸多方法开展了无拖曳控制器设计、系统分析与仿真，而上述无拖曳控制理论研究多数未考虑执行机构的实际特性，将其理想化或添加高斯白噪声，实际上微牛级推力器的输出特性直接约束无拖曳控制的设计过程及最终精度上限。

本文以微波离子推力器为执行机构展开无拖曳控制研究，其具备比冲高、推力范围广、推力估计准确度高、调节速率快等众多优点，但也存在非预期电击穿（打火）问题，在控制角度上，会导致瞬时推力波动，使得预定的正常工作被临时中断、连续稳定推力状态被破坏等情况。离子推力器在地面或空间实验环境下都会出现打火现象[22-24]，通过各种防护措施可以将打火的频次及影响降低，但打火问题还是难以完全解决，其源于离子推力器内在工作特性及多种因素的复杂耦合[25-28]。

引力波探测卫星处于空间环境，需利用微牛级推力器产生推力抵消外部非保守力，但也带来较严重的低频输出扰动，同时静电耦合力、电容传感器量测噪声的存在也会影响控制精度，因此对无拖曳控制系统的鲁棒性与噪声抑制能力提出极高要求。

此外，为了避免卫星实际应用中存在的通信延时、推进系统响应延时、惯性传感器测量与计算延时等诸多因素带来的影响，对无拖曳控制系统提出超低带宽要求，本文将带宽定于0.1 Hz，从而使系统具备极强的延时包容性。

然而，在超低带宽约束下，一般线性控制器难以同时兼顾强鲁棒性与噪声抑制能力，难以完全实现控制精度要求。

因此，本文研究采取分数阶PID作为无拖曳控制器，分数阶PID的优势在于能够选择合适的分数阶积分和微分参数来实现更加精确的控制性能，在同带宽、稳定裕度约束下能够实现更强的鲁棒性与稳态精度。

1 无拖曳卫星动力学建模

1.1 参考坐标系

地心惯性坐标系（Exeyeze）：其坐标原点位于地心E；ze轴指向J2000历元地球北极的平均位置处；xe轴在赤道平面内，指向J2000历元的春分点；ye轴在赤道平面内与xe轴垂直，且与xe轴、ze轴构成右手正交坐标系。

卫星质心轨道坐标系（Ox0y0z0）：其坐标原点位于卫星质心O；z0轴由地心E指向卫星质心O；x0轴在轨道平面内与z0轴垂直；y0轴与轨道平面正法线方向一致，且与x0轴、z0轴构成右手正交坐标系。卫星空腔坐标系（Oixiyizi，i=1,2）：这两个坐标系用于对无拖曳指标的评测，其坐标原点Oi位于检验质量所处的空腔中心；xi轴指向激光干涉方向即为敏感轴；yi轴与轨道平面正法线方向一致，zi轴与xi轴、yi轴构成右手正交坐标系。

参考坐标系示意图如图1所示：

图1 参考坐标系Fig.1 Reference coordinate system

1.2 动力学模型

本文研究了包含两个检验质量（Test Mass）的无拖曳卫星，其敏感轴夹角呈60°，当卫星和两个检验质量处于标称位置时，它们的质心位于一条直线。在惯性坐标系（Exeyeze）中，考虑扰动的影响，卫星和检验质量的动力学模型分别如下

其中：rsc=[xsc,ysc,zsc]T是地球质心到卫星质心的位置矢量；rtmi=[xtmi,ytmi,ztmi]T是地球质心到检验质量；TMi(i=1,2)为质心的位置矢量；µ=GM是标准重力参数；msc=250kg是卫星平台的质量；mtmi=2.45 kg是检验质量的质量；usc=[uscx,uscy,uscz]T、utmi=[utmix,utmiy,utmiz]T分别是针对卫星和检验质量的控制力矢量；fsc=[fscx,fscy,fscz]T、ftmi=[ftmix,ftmiy,ftmiz]T分别是卫星和检验质量受到的扰动力矢量。

将式（1）减去式（2）得出相对动力学模型

将式（3）转换到卫星质心轨道坐标系（Ox0y0z0）中可得式（4）速度。

其中：ωe、分别为卫星质心轨道坐标系（Ox0y0z0）相对于地心惯性坐标系（Exeyeze）的角速度矢量、角加速度矢量。

将式（4）展开，可得非线性公式（5）

为了方便控制器的设计，将其简化并转换成状态方程如式（6）

根据式（6）得出被控对象的传递函数

式（7）中各自由度存在相互耦合的情况，通常将目标矩阵的逆矩阵引入到控制回路中，以实现解耦[29]。

2 推力器输出特性及扰动分析

2.1 微波离子推力器输出特性

微波离子推力器实验装置如图2所示，推力器有三大调控部件：电压源、微波源、贮供单元，其中用于工质电离的4.2 GHz微波源输出功率为0.5～5 W，提供离子引出电场的屏栅电压为200～1 000 V、加速栅电压为–40～–200 V，作为推进剂的氙气流量设定为6～20 μg/s。

图2 微波离子推力器实验装置Fig.2 Microwave ion thruster experimental setup

目前，微波源自身响应时间约1 ms，电压源约50 ms，而贮供单元的调控响应时间则长达数秒之久，为实现50 ms推力器响应时间指标，需将微波源调控输出推力作为主要手段，通过微波源开环调节推力器输出推力的响应曲线如图3（a）所示，响应时间约为5 ms，控制系统设计时可视其具备理想的动态特性。因微波离子推力器由微波主导放电，即工质流量固定时，引出电流大小主要由微波功率决定。10 μg/s氙气流量下不同微波功率及电压对应的输出推力值如图3（b）所示，当选取适中的电压值时，通过快速调节微波功率便能实现几十μN的推力输出范围。

图3 推力器响应速度及调控范围Fig.3 Thrust response speed and control range

对于本文研究的双栅离子推力器，电击穿主要存在于屏栅与加速栅之间，当推力器工作不稳定时会出现如图4（a）所示的屏栅、加速栅短路打火（存在于1 503 s、1 775 s ），此时推力下降至0 μN。推力器短路打火带来的噪声如图4（b）红色部分所示，蓝色部分是将打火尖刺滤除后的推力噪声，其在0.01～1 Hz频段下降了一个数量级，说明打火带来的噪声影响主要分布在0.01～1 Hz频段。

图4 推力器打火现象及噪声分析Fig.4 Analysis of fire phenomenon and noise of thruster

如图5（a）所示，推力器输出推力因实验环境温度变化产生漂移，推力温漂噪声如图5（b），其在1 mHz～0.01 Hz频段超出0.1 μN/Hz1/2推力噪声指标需求，上述噪声特性和输出约束是控制器设计时必须考虑之处。

图5 推力输出噪声特性Fig.5 Thrust output noise characteristics

2.2 扰动分析

本文研究中，主要考虑卫星内外部两个影响较大的扰动力。

1）静电耦合力

卫星内部的两个检验质量位于电容腔室之中，主要受到静电耦合力的影响

其中，ke=−2.3×10−7N·m−1为电容传感器自身产生的负静电寄生刚度[30]。

2）太阳光压辐射扰动

卫星编队处于约十万km的地球轨道高度，不可避免的受到各种外部扰动的影响，其中太阳光压fsc的影响较大，是无拖曳控制系统需要主要抵消的扰动之一，其时域、频域分析如图6所示，从图6（a）可以看出敏感轴X1上的光压水平达到了46 μN，从图6（b）可以看出，太阳光压夹杂的噪声水平在0.1 mHz超过0.1 μN/Hz1/2。

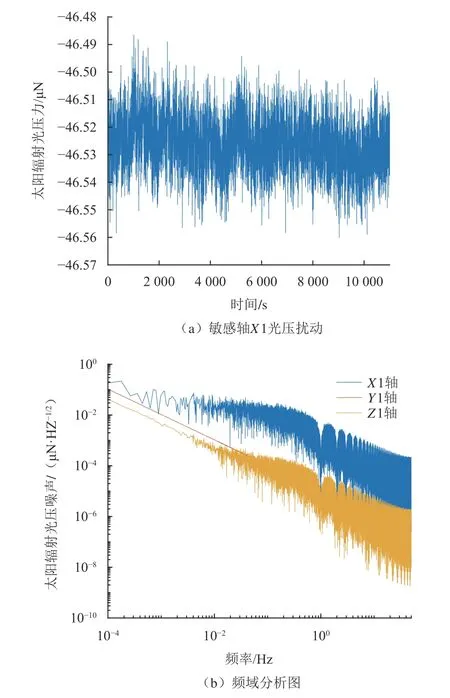
图6 太阳光压辐射扰动Fig.6 Solar radiation perturbation

3 控制系统设计

3.1 无拖曳控制策略

无拖曳卫星在绕地心轨道运动时，会受到太阳光压、地球引力、非球体扰动、以及内部静电干扰等影响，若不采取控制补偿或补偿裕度不足时，会使得卫星、检验质量发生碰撞，造成无法修复的机械损伤。

实际中，卫星无法同时跟踪两个检验质量来保持相对位移，故提出一种新的控制模式，如图7所示，期望保持检验质量1在纯引力状态下运动，故不对其施加任何控制力，此时利用微推力器推动卫星跟踪检验质量1来维持它们的相对距离。同时也为了避免控制力的引入而影响到检验质量2在无拖曳控制指标要求0.1 mHz到1 Hz频段的残余加速度水平，需要在0.1 mHz静电力控制系统带宽约束下通过施加静电力到检验质量2上从而实现其对卫星的跟踪，此方案最终能够实现三者的高微重力水平。

图7 双检验质量卫星控制方法Fig.7 Dual test mass satellite control method

3.2 控制器设计

空间引力波探测“天琴计划”要求在0.1 mHz～1 Hz频段内，卫星与检验质量的相对位移ei(i=1,2)低于1 nm/Hz1/2及检验质量的残余加速度ai(i=1,2)低于10–15m/s2/Hz1/2，其定义如下

其中

本文决定采用分数阶PID控制器来实现目标，控制框架如图8所示：

图8 双检验质量无拖曳控制框图Fig.8 Dual test mass drag-free control block diagram

分数阶PID控制器[31-32]的传递函数如式（10）所示，由于引入了 λ、µ 两个指数变量，使得控制器在同系统约束下能够实现更优的控制性能。

令s=jω，代入式（10）得

其中：r为实部，s为虚部，根据棣莫弗定理

得出

将式（13）代入式（10）得到最终分数阶PID控制器的频域传递函数

假设推力器工作状况稳定，推力噪声低于推进系统0.1 μN/Hz1/2指标要求，则推力输出usc到相对位移r1的闭环传递函数PS(jω)在0.1 mHz到1 Hz频段的任意幅值需要低于–40 dB，才能实现低于1 nm/Hz1/2的相对位移指标，同时为了兼顾控制系统0.1 Hz超低带宽要求、稳定裕度需求、噪声抑制能力，对无拖曳控制回路提出相应频域约束：

i.穿越频率

ii.相位裕度

iii.高频噪声抑制约束

iv.扰动抑制约束

以式（15～17）作为约束条件，式（18）为目标函数通过遗传算法求解出微推进系统最优分数阶PID控制器参数，其传递函数如下

根据上述设计可以得到无拖曳控制回路开环Bode图及闭环控制系统的混合灵敏度函数如图9所示，从图9（a）可以看出无拖曳控制回路带宽满足0.1 Hz要求，相位裕度满足45°，满足稳定性能要求。从图9（b）可以看出其扰动抑制能力在全频段基本实现至–40 dB以下，可对推力器打火噪声、光压扰动具备较高抑制能力，高频噪声抑制约束也在1 Hz实现至–20 dB以下，具备对电容传感器高频量测噪声的抑制能力。

图9 无拖曳控制回路频域特性图Fig.9 Drag-free control loop frequency domain characteristic diagram

同样设计得出静电力控制器K2(s)传递函数如式（20），其频域分析如图10所示。从图10（a）可以看出静电力控制系统带宽满足0.1 mHz要求，相位裕度满足45°。从图10（b）卫星控制器在0.1 mHz以下具有较强的输出干扰抑制，在0.1 mHz以上具有较好的噪声抑制能力。

图10 静电悬浮控制回路频域特性图Fig.10 Frequency domain characteristic diagram of electrostatic suspension control loop

4 性能仿真及对比分析

4.1 分数阶PID控制性能

本节将进行无拖曳控制系统性能仿真验证，实验环境如表1所示，在固定推力器电压及工质流量的条件下，通过开环调节离子推力器微波源来实现推力输出的变化，进而推动卫星跟踪检验质量1。

表1 实验环境Table 1 Experimental environment

为了体现推力器打火及固有噪声同时带来的影响，绘制了一万s无拖曳模式工作下的推力输出曲线如图11（a）所示，一共打火80次，其中最大的推力打火波动出现在1 111.54 s，离稳态输出的46.5 μN瞬间下降了7～39.5 μN，从图11（b）的功率谱密度可以看出推力器输出推力噪声在1 mHz～0.1 Hz频段低于0.1 μN/Hz1/2，其余频段略微超出0.1 μN/Hz1/2，势必会给控制精度带来影响。

图11 无拖曳控制推力噪声分析Fig.11 Drag-free control thrust noise analysis

敏感轴X1的控制精度指标如图12（a）、（b）中的蓝色部分所示，相对位移精度在全频段优于1 nm/Hz1/2及检验质量的残余加速度低于10–16m/s2/Hz1/2，满足指标要求。具体可以看出在0.1 Hz附近的相对位移稍微高一点接近1 nm/Hz1/2，原因在于前面所示的推力噪声从0.1 Hz开始超出了0.1 μN/Hz1/2，同时分数阶控制系统的扰动抑制幅值jPS(jω)j在0.1 Hz附近频段处于最大值约–40 dB（图10（b）)，即对推力噪声的抑制能力最弱。同时1 mHz以下频段的扰动抑制幅值从–50 dB并往下一直降低，即系统对推力噪声的抑制能力在低频段逐渐增强，解释了推力器噪声在1 mHz以下超出0.1 μN/Hz1/2，相对位移精度却能实现10–10m/Hz1/2这一现象。

图12 分数阶PID无拖曳控制结果Fig.12 Fractional-order PID drag-free control results

从图12（c）、（d）可以看出，检验质量2的3个自由度X2、Y2、Z2方向上的无拖曳控制精度都满足了指标要求，前文将静电力控制系统带宽设置在0.1 mHz，是为了避免检验质量2在耦合力的长期影响下与卫星发生碰撞，同时也避免在指标0.1 mHz-1 Hz频段引入的控制信号干扰到检验质量2的残余加速度水平，所以检验质量2的无拖曳实现精度很大程度上取决于卫星的微重力水平，即卫星跟踪检验质量1的无拖曳水平。

当实验环境温度产生变化时，会使推力器稳态输出推力产生漂移，导致推力输出准确度下降。但通过外环无拖曳系统控制器自动上调推力指令使得推力器实际输出推力达到所需稳定值，如图13所示，可见控制器能够有效抑制推进系统温漂带来的扰动影响。

图13 推力温漂及控制抑制效果Fig.13 Thrust temperature drift and control suppression effect

4.2 对比分析

为了对比控制性能，本文也在相同频域约束下设计了线性PID微推进控制器C1(s)及静电力控制器C2(s)，其传递函数如式（21）、（22），频域分析如图14所示。为了兼顾控制系统的稳定性及鲁棒性，将微推进控制系统带宽做到0.1 Hz、相位裕度做到45°的时候，系统扰动抑制能力最高实现至–30 dB，比分数阶PID控制系统高了10 dB，即扰动抑制约束能力要弱一些。

图14 PID控制系统频域特性图Fig.14 Frequency domain characteristic diagram of PID control system

PID无拖曳控制系统仿真结果如图15所示，从图15（a）可以看出敏感轴X1的相对位移精度在0.05 Hz附近超出了指标，从图15（c）、（d）可以看出在0.1 mHz频段检验质量2的相对位移与残余加速度均有超出指标的情况，主要原因还是线性PID受限于整数阶系统传递函数特性，在相同系统约束下能够实现的综合性能上限低于分数阶PID，即系统的扰动抑制能力不足，导致其无法完全抑制推力器噪声及各种扰动，最终卫星与检验质量间微重力水平遭到破坏。

图15 PID无拖曳系统控制结果Fig.15 PID drag-free system control results

5 结 论

本文针对微波离子推力器输出特性展开了分析，将推力器打火、温漂带来的低频噪声影响转化为控制器频域上的约束，并设计了分数阶PID控制器。仿真结果表明，本文设计的分数阶PID控制器可以兼顾无拖曳控制系统超低带宽、强鲁棒性、高频噪声抑制能力等多重性能要求，在反馈控制框架下，相较于线性PID控制器具有更好的抗扰动能力、实现了更高的精度指标。