基于EEMD-KELM 的淮安市二河溶氧量预测研究

陈 肖，张 强，姚年春

（江苏财经职业技术学院智能工程技术学院，淮安 223300）

0 引言

淮安市二河位于洪泽湖东侧，其水量主要来自于洪泽湖的补给。作为淮安市重要的河流型水源地，已经被纳入了水利部公布的第二批《全国重要饮用水水源地名录》［1］。二河支撑着淮安市城南区域灌溉、养殖、供水等活动，近年来，洪泽湖透明度降低，湖体富营养化严重，因二河主要由洪泽湖通过二河闸供水，二河水质也不断恶化［2］。溶氧量（dissolved oxygen, DO）作为一项重要的水质参数，随着季节的变化有规律的波动。DO 可以指示河流的受污染程度，也能从中分析得出鱼、虾等水生生物的生存条件［3］。因此，对于DO 发展趋势的精确预测，对水源地的水质管理以及淮安市的经济及社会可持续发展具有重要意义，同时也能为二河的饮用水源地保护提供一种新的思路。

基于上述分析，本文将集合经验模态分解（ensemble empirical mode decomposition, EEMD）与核极限学习机（kernel extreme learning machine, KELM）组合，运用在淮安市二河溶氧量的预测中。将EEMD 分解得出每个分量的KELM预测结果叠加，作为整个组合模型的最终预测结果。与其他预测模型相比，本文提出的模型预测精度高、泛化性强，可以实现对二河水质的高精度预测。

1 EEMD-KELM 预测模型的构建

1.1 EEMD

EEMD 基于经验模态分解（empirical mode decomposition, EMD），在EMD 的基础上将数个高斯白噪声加入到待分解的信号中，再将所有的分解结果相加取均值以得出最终的本征模态函数（intrinsic mode function, IMF），以此优化EMD 中的模态混叠问题，具有良好的分解效果［4］。IMF 分量利用三次样条插值法，可以实现对原始序列的筛分，第一个被筛分出来的IMF分量通常频率最高，之后的IMF 分量频率依次降低。当分解达到终止条件时，剩余未被筛分的序列称之为残差。EEMD的分解步骤如下：

（1）将数个高斯白噪声信号εi(t)加入到原始信号序列x(t)中，得到加噪信号xi(t)：

式中：i表示加入的高斯白噪声的个数。

（2）将加噪信号xi(t)按照EMD 分解的步骤分解，分解过程参照文献［5］，得到i个加噪信号的IMF 分量cn,i(t)，然后对cn,i(t)进行整体平均，得出的第n个IMF分量可表示为

式中，n为IMF 分量的个数。对残差的处理同样参照上式，此处不再赘述。

对于白噪声的添加，根据EEMD 算法提出者的要求，应满足：

式中，εn为IMF 重构信号与初始信号的误差，经过查阅其他文献与实验验证，本文将i的取值设置为100，ε的取值为0.1 时有较好的分解效果，可以有效避免模态混叠的发生。

1.2 KELM模型

1.2.1 极限学习机

ELM算法是Huang等［5］提出的一种单隐层前馈神经网络算法，其输入层与隐含层的权值阈值随机产生，只需要设置好隐含层节点数即可直接得到隐含层到输出层的权值，其数学模型为

式中：H为隐含层输出矩阵；Y为输出矩阵；β为隐含到输出层的连接权值矩阵。求解式（4）的最小二乘解：

解出β=H+Y。H+为隐含层输出矩阵的摩尔彭罗斯广义逆矩阵。

1.2.2 核极限学习机

KELM 是基于ELM 发展而来，传统的ELM算法为了实现高效快速的训练效果牺牲了一定的稳定性与泛化性。因此，Huang 等［5］提出采用核函数h(x)来代替随机映射H，由此将样本从复杂的低维度空间问题映射到高维空间转化为内积问题［6］。在此基础上，引入正则化系数C以提高模型的稳定性与泛化性，解决模型的系统性风险，进一步提升了模型的预测能力［7］。引入正则化系数C后，ELM 学习过程由最小二乘最优解转变为求解二次规划问题，利用拉格朗日乘数法求解得出：

式中，C为正则化系数，根据Mercer’s 条件［8］，将核矩阵定义为

式中，K(*) 为核函数，本文选择高斯核函数，因此：

式中，g为核参数，KELM的预测输出为可以看出，核参数g以及正则化系数C的选取十分重要，可以决定KELM的预测性能。

1.3 EEMD-KELM组合模型

EEMD-KELM 二河水质DO 值组合预测模型的整体预测流程如图1所示。

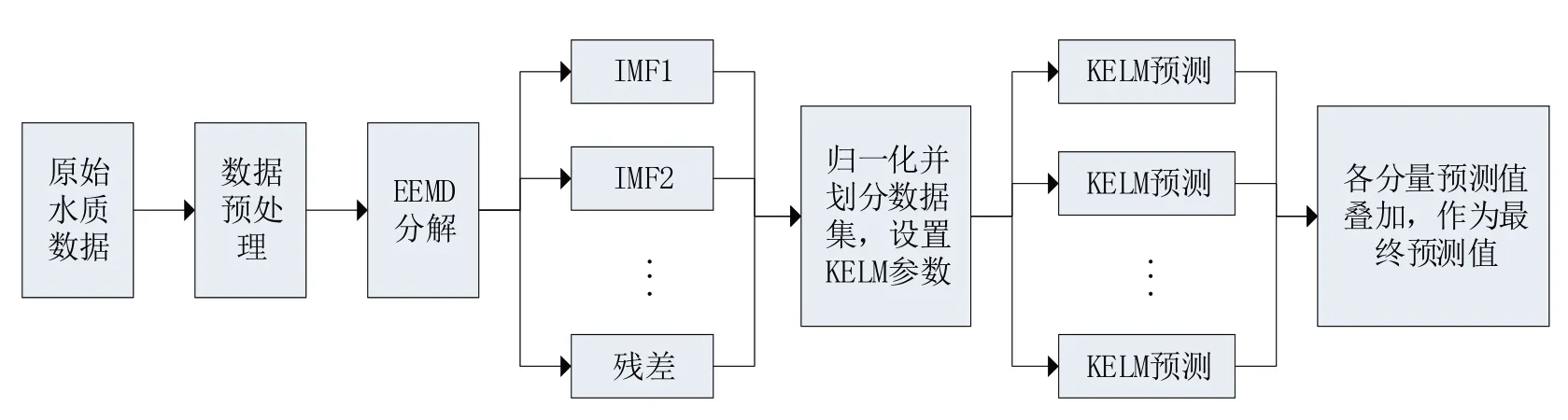
图1 EEMD-KELM预测模型整体流程

2 二河水质DO值的组合模型预测

2.1 水质数据处理

数据集使用淮安市环境局提供的2010 年第1 周至2020 年第50 周共537 周的水质DO 数据。利用箱线图法对水质DO 值数据集中的异常值进行剔除。利用均值平滑法对异常值和缺省值进行修复，如果需要修复的数据连续分布，则基于相似日的方法，通过查询缺失数据所在周的气象信息与水文信息，寻找相似周数的水质数据的均值作为最终的修复值［9］。

利用EEMD 算法对二河的DO 序列进行分解，利用1.1 的数据设置好EEMD 的相关参数，分解的结果如图2所示。

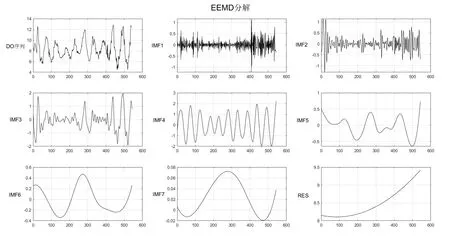
图2 二河DO序列EEMD分解结果

由图2 可知，二河的DO 序列被分解成7 个IMF 分量和一个残差，这些分量反映出了二河DO 值的变化情况，使得原来难以预测的DO 序列有规律可循。在这些分量中，IMF1与IMF2的频率最高，表现出的特征类似噪声，该分量反映出了二河DO 值的随机变化，可以称之为随机分量。IMF3、IMF4 与IMF5 反映的是二河DO 序列有规律的变化细节，易于拟合与掌握，统称为细节分量。IMF6、IMF7 以及残差Res 反映的是二河DO 序列的整体变化趋势，称之为趋势分量。由于IMF6 与IMF7 的量纲较小，为了提升算法的运行效率，本文选择叠加趋势分量，将叠加后的分量作为一个新的分量带入模型预测，简化模型预测过程。

这里以IMF1 为例，利用分布式取值法构建数据集，即每10 个为一组，一组内的前9 个作为输入，第10 个作为输出。因此，543 个数据可以创建534 组数据，取前510 组作为训练集，剩下的24 组为测试集。剩余的其它分量都以此方式创建数据集并按统一的标准设定训练集和测试集。

2.2 二河DO值预测对比分析

依然以IMF1 为例，本文参照文献［10］，利用麻雀搜索算法对KELM 的g、C、以及隐含层节点数进行寻优。设定麻雀搜索算法的最大迭代次数是100，种群大小是30，其中隐含层节点数的寻优范围设定为［10，250］，正则化系数C的范围设定在［0.001，10］，核参数g的范围设定在［0.001，10］。最终将IMF1 分量的KELM 参数设定为：107 个隐含层节点，核参数g设定为2.054，正则化系数C设定为1.685。其它分量的设置方法与IMF1 分量设置方法类似，此处不再赘述。使用KELM 对各分量进行预测，为降低偶然性因数的影响，取预测结果30 次的平均值作为最终预测结果，将各分量预测结果叠加，作为最终的预测结果。

为验证EEMD-KELM 模型预测效果，将其与支持向量机（support vector machine, SVM）、KELM 以及长短时记忆网络（long short time memory, LSTM）进行对比。为了保证结果的客观，在计算预测结果时同样采用30 次实验的平均值作为最终结果。本次研究的评价指标选择均方根误差（root mean square error, RMSE）与平均绝对百分误差（mean absolute percentage error,MAPE）。EEMD-KELM 与其他模型的预测数据比较结果如图3所示。为了直观地比较和分析各模型的预测性能，各个预测模型的RMSE 及MAPE如表1所示。

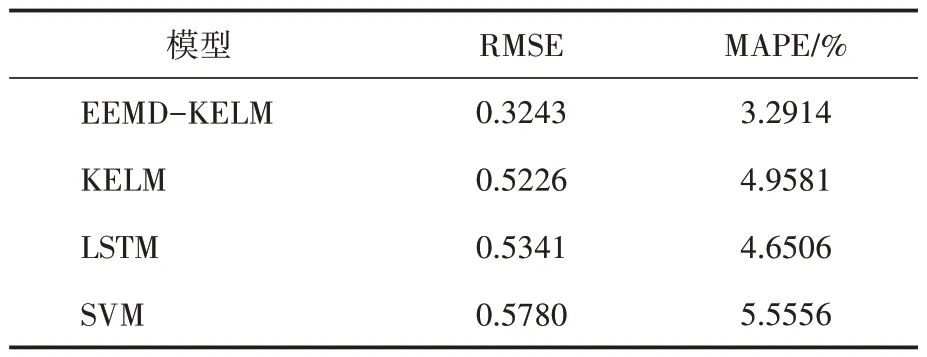
表1 二河DO值预各测模型参数评价对比

图3 二河DO值各预测模型预测值与真实值对比

从图3可以看出，EEMD-KELM 模型预测性能良好，能够以较高拟合度与精度对二河DO 值进行预测。因此，“分解—预测—结合”的预测思路是十分有效的，EEMD 有效地解耦了二河的水质DO 值数据，使得KELM 能够高效地实现对每个分量的预测，组合预测模型极大地提高了二河DO值的预测精度。

由表1可知，EEMD-KELM 模型具有最高的预测精度。在与其他模型的比较中，EEMDKELM 模型的RMSE 比SVM 降低了43.89%；比KELM 降低了37.94%；比LSTM 降低了39.28%。其MAPE 比SVM 降低了40.76%；比KELM 降低了33.62%；比LSTM 降低了29.23%。由此得出，EEMD-KELM模型预测精度高、泛化性强。能够较为准确地预测二河水质DO 值的变化，可以为二河的水环境保护与治理等活动提供决策依据。

3 结语

本文将核函数与正则化系数引入极限学习机，提高了极限学习机的泛化性与预测稳定性。利用EEMD 解耦二河水质数据，并将解耦所得分量分别代入KELM 模型进行预测，将各分量预测结果叠加作为最终预测结果。结果表明，与其他预测模型相比，本文所提模型能够对二河DO值进行准确预测，泛化性强、预测精度高。

在水环境保护呼声渐涨的当下，如何实现对流域环境的高效治理与保护正逐渐成为一项重要的研究工作，而水质预测作为上述工作的基础，应具有较好的预测能力和稳定性，以此为从业人员提供参考。本文提出的模型能够实现上述目标，因此具有一定的使用前景。

在后续的研究中，可以将其他的水质参数与天气因素考虑在内，实现多因素的预测方法。另外，还可对解耦算法进行改进，提高随机分量的预测能力，从而进一步提高水质预测模型的预测精度和稳定性。