基于改进差分进化的Hammerstein系统辨识
刘梦茹 李俊红 徐珊玲
(南通大学电气工程学院 江苏 南通 226019)
0 引 言
系统辨识是研究建立系统数学模型的理论与方法。近几十年来,系统辨识已经成为控制理论的一个十分活跃而又重要的分支[1]。在非线性系统辨识方面,一些智能辨识算法如遗传算法、粒子群优化算法和神经网络算法取得了较好的结果[2]。
大部分非线性系统可以用Hammerstein或者Wiener模型来描述。Narendra等[3]最早于1966年提出关于此类模型的辨识方法,他们将Hammerstein模型分成线性的动态子系统和非线性的静态子系统。目前为止,许多研究人员已经提出一些算法用于辨识Hammerstein非线性系统,比如最小二乘算法、随机梯度算法等[4]。由于传统辨识算法对于Hammerstein系统辨识往往存在辨识精度不够高、收敛速度较慢等问题,尤其是针对含有有色噪声的Hammerstein模型。近年来,启发式群智能优化算法成为解决复杂问题的热门选择,受到广泛关注。其中,DE算法是一种典型的启发式算法,最早由Storn等[5]提出,目的是求解切比雪夫多项式问题。DE算法自提出以来,因其控制参数少、鲁棒性强等优点,已经成为进化计算领域的研究热点之一。
然而,基本DE算法存在局部最优的问题。针对这一现象,许多研究者对DE算法进行了改进。Fan等[6]提出了ZEPDE算法,用于控制参数且分区自适应变异策略。Tvrdik等[7]提出将DE算法和K均值算法结合的新算法,通过聚类中心加快搜索速度。Wang等[8]提出一种基于搜索数据分析的自适应差分进化算法用于解决多目标优化问题,采用多个子种群协同进化。卢峰等[9]为解决DE算法中存在的过早收敛和搜索停滞的问题,根据个体适应度值的大小将种群分成三个不同的子种群,采取不同的变异策略,加快了算法的收敛速度。Biswas等[10]为减少选择阶段的计算提出了LoINDE算法。
针对Hammerstein受控自回归滑动平均(CARMA)模型,本文利用改进DE算法对该模型进行参数辨识,为了证明改进算法的有效性和可行性,本文还推导了递推最小二乘(Recursive Least Squares,RLS)算法,在仿真实验中将改进DE算法与RLS算法、基本DE算法和粒子群(PSO)算法对比,验证了改进DE算法的有效性。
1 系统描述
Hammerstein CARMA模型如图1所示。其中:u(t)是模型输入信号;y(t)是模型输出信号;v(t)是白噪声;w(t)是有色噪声。

图1 Hammerstein CARMA模型
假设y(t)=0,u(t)=0,m(t)=0且v(t)=0(t≤0)。非线性部分方程为:
m(t)=f(u(t))=γ1f1(u(t))+γ2f2(u(t))+
…+γmfm(u(t))=f(u(t))γ
(1)
f(u(t))=[f1(u(t)),f2(u(t)),…,fm(u(t))]∈R1×m
(2)
式(2)是基函数构成的行向量。而非线性部分的参数向量γ可以表示为:
γ=[γ1,γ2,…,γm]T∈Rm
(3)
线性部分的方程为:
A(z-1)y(t)=B(z-1)m(t)+D(z-1)v(t)
(4)
其中:
噪声部分为:
式中:z-1是单位后移算子。
z-1y(t)=y(t-1)
(7)
式中:A(z-1)、B(z-1)和D(z-1)是z-1的常数系数时不变多项式,可以定义为:
A(z-1)=1+a1z-1+a2z-2+…+anz-na=
B(z-1)=b0+b1z-1+b2z-2+…+bnz-nb=
D(z-1)=1+d1z-1+d2z-2+…+dnz-nd=
式中:aj、bj、dj和γj是要估计模型的未知参数,并且阶数na、nb、nd和m是已知的[11]。我们假定多项式B(z-1)的首项b0=1,定义参数向量η和信息向量φ(t)如下:
η=[a1,a2,…,ana,b1,b2,…,bnb,γ1,γ2,…,
γm,d1,d2,…,dnd]T∈Rn
(11)
n=na+nb+nd+m
φ(t)=[-y(t-1),-y(t-2),…,-y(t-na),
m(t-1),m(t-2),…,m(t-nb),
f1(u(t)),f2(u(t)),…,fm(u(t)),
v(t-1),v(t-2),…,v(t-nd)]T∈Rn
(12)
则Hammerstein CARMA系统可以表示为:
通过式(11)-式(13),可以得到如下辨识模型:
y(t)=φT(t)η+v(t)
(14)
定义目标函数:
(15)
式中:l是数据的长度;J1(k)表示DE算法适应度函数。下面用改进DE算法和RLS算法分别对Hammerstein CARMA模型进行辨识。
2 差分进化算法
2.1 基本差分进化算法
DE算法是基于群体智能理论的优化算法,通过种群内个体间的合作竞争产生的群体智能指导优化搜索[12]。DE算法的核心步骤是变异操作、交叉操作和选择操作。
2.1.1生成初始群体
在初始化阶段,需要在n维空间里确定算法的基本参数,包括种群大小M、变异因子F、交叉因子ω和最大迭代次数G,具体措施设置如下:
i=1,2,3,…,M
(16)
j=1,2,3,…,n
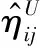
2.1.2变异操作
变异操作是种群中随机选择3个个体,任取两个个体的向量差加权后按一定的规则与第三个个体求和而产生变异个体[13]。基本的变异操作可表示为:

2.1.3交叉操作
交叉操作是为了增加群体的多样性[14]。变异个体与某个预先决定的目标个体进行比较,生成实验个体,将交叉因子定义为ω,具体操作如下:

2.1.4选择操作

(19)

2.2 改进差分进化算法
相比传统算法,基本DE算法具有收敛速度快和鲁棒性强的特点,但算法中仍然存在许多值得进一步研究的问题。种群的大小将影响计算的复杂性,而变异因子F和交叉因子ω是控制种群多样性和收敛性的重要参数[16]。
变异操作和交叉操作两个过程是相辅相成,互相影响的,因此对DE算法的变异过程和交叉过程进行改变,将变异因子F和交叉因子ω从固定值变成自适应动态值,以提高算法的精度和有效性。
2.2.1改进的变异操作
变异因子F在算法中起调节作用[17],为了使算法最有效地逼近最优解,在变异操作中引入了自适应算子α,具体改进策略如下:
F=F0×2α
(21)
式中:F0是初始变异系数;自适应算子α为周期函数;G为最大迭代次数;k为当前迭代次数(1≤k≤T)。在基本DE算法中,变异因子F取常数值,难以确定最优值,而引入具有周期性质的自适应算子,以动态值来代替基本算法的静态固定值,让变异因子的搜索范围始终处在一个合理的范围内,随着迭代次数不断地增加,变异因子F也在不断改变寻找最优值,在初期可以保持多样性,防止过早收敛。
2.2.2改进的交叉操作
为了提高算法的优化性能,交叉运算自适应调整策略可以更好地平衡全局和局部搜索能力,算法可以更快地搜索最优解。具体的改进策略为:
ω=0.6×(1+rand())
(23)
式中:rand()是[0,1]之间的随机数。
改进DE算法用于估计参数向量η的公式总结如下:
(24)
F=F0×2α
(27)
ω=0.6×(1+rand())
(29)

(31)
改进DE算法估计参数η的步骤如下:
1) 初始化种群,设置初始参数,包括种群大小M、参数个数D、最大迭代次数G和初始变异因子F0。
2) 设置当前种群的最优个体,通过式(25)进行初始化。
3) 根据式(24)计算群体中每个个体的适应值。
4) 根据式(26)-式(28)执行变异操作。
5) 根据式(29)-式(30)执行交叉操作。
7) 确定是否满足终止条件k>G,如果满足此条件,则产生最优个体,否则返回步骤3)。
改进DE算法的流程如图2所示。

图2 改进DE算法流程
3 递推最小二乘算法

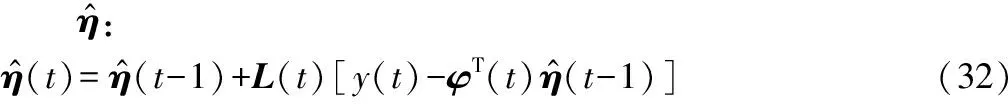
L(t)=P(t-1)φ(t)[1+φT(t)P(t-1)φ(t)]-1
(33)
P(t)=[I-L(t)φT(t)]P(t-1),P(0)=p0I
(34)
式中:L(t)为增益向量,P(t)为协方差矩阵。
L(t)=P(t)φ(t)∈Rn×n
(35)
4 仿真分析与结果
考虑以下Hammerstein CARMA系统:
A(z-1)y(t)=B(z-1)m(t)+D(z-1)v(t)
A(z-1)=1+a1z-1+a2z-2=1-1.132z-1+1.1z-2
B(z-1)=1+b1z-1+b2z-2=1+z-1-1.14z-2
m(t)=f(u(t))=γ1f1(u(t))+γ2f2(u(t))=
0.091u(t)-0.148u2(t)
D(z-1)=1+d1z-1+d2z-2=1+0.98z-1-1.5z-2

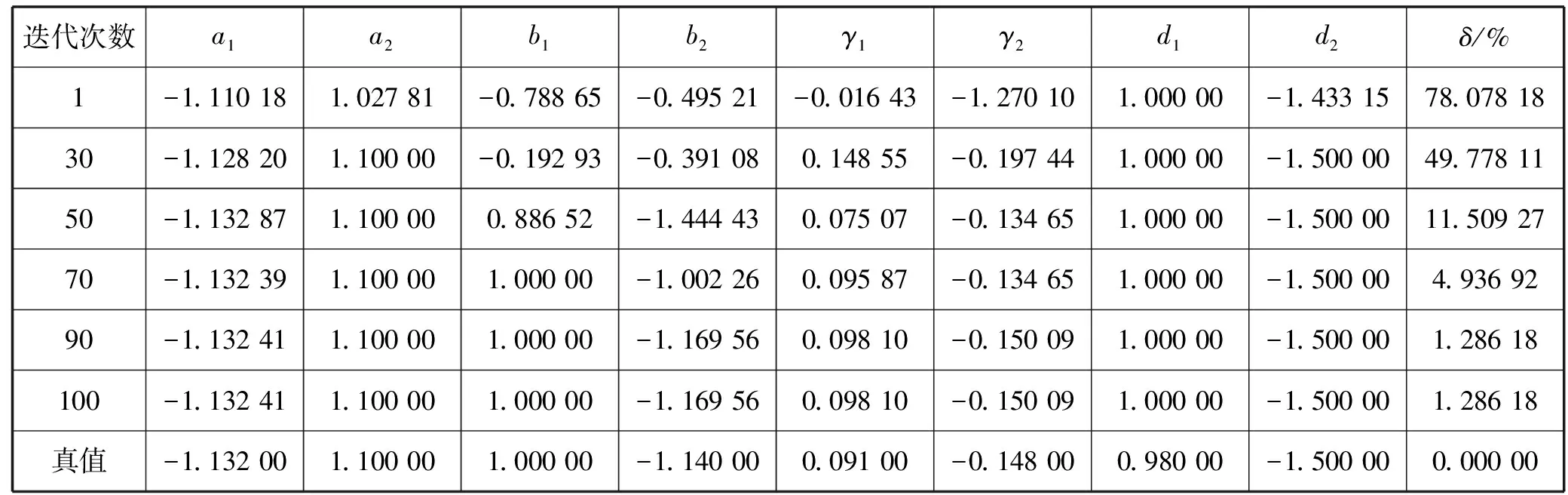
表3 DE算法参数估计与误差

表4 PSO参数估计与误差

图3 改进DE算法估计误差曲线

图4 改进DE算法适应度演化曲线

图6 DE算法估计误差曲线

图7 PSO估计误差曲线
可以看出,在噪声方差为σ2=0.102的情况下,改进DE算法和RLS算法的估计误差越来越小,改进DE算法比RLS算法、基本DE算法和PSO具有更高的辨识精度和更快的收敛速度。
5 应用实例
控制反应器的反应物浓度一直以来都是化工过程控制领域的研究热点,连续搅拌反应釜是工业过程中广泛应用的一类反应器[20],如图8所示,反应釜工作时,搅拌器快速搅拌,容积内部浓度相等。反应釜夹套冷却水带走反应产生的热量,保持釜器内各处温度相等和稳定[21]。
连续搅拌反应釜可以建模为Hammerstein模型结构[22]。在图8展示的连续搅拌反应釜中,非线性部分为多项式函数,线性部分为CARMA结构,模型为:
A(z-1)=1+a1z-1+a2z-2=1-0.918z-1+0.286z-2
B(z-1)=1+b1z-1+b2z-2=1+z-1-1.5z-2
m(t)=f(u(t))=γ1f1(u(t))+γ2f2(u(t))=
-0.07u(t)+0.383u2(t)
D(z-1)=1+d1z-1+d2z-2+d3z-3=
1+0.56z-1-0.925z-2+0.46z-3
模型的线性部分参数为:
a=[-0.918,0.286],b=[1,-1.5],d=[0.56,-0.925,0.46]
多项式函数的系数为:
γ=[-0.07,0.383]
将改进DE算法用于连续搅拌反应釜的辨识,辨识误差曲线结果如图9所示,适应度演化曲线如图10所示。

图9 连续搅拌反应釜辨识误差曲线
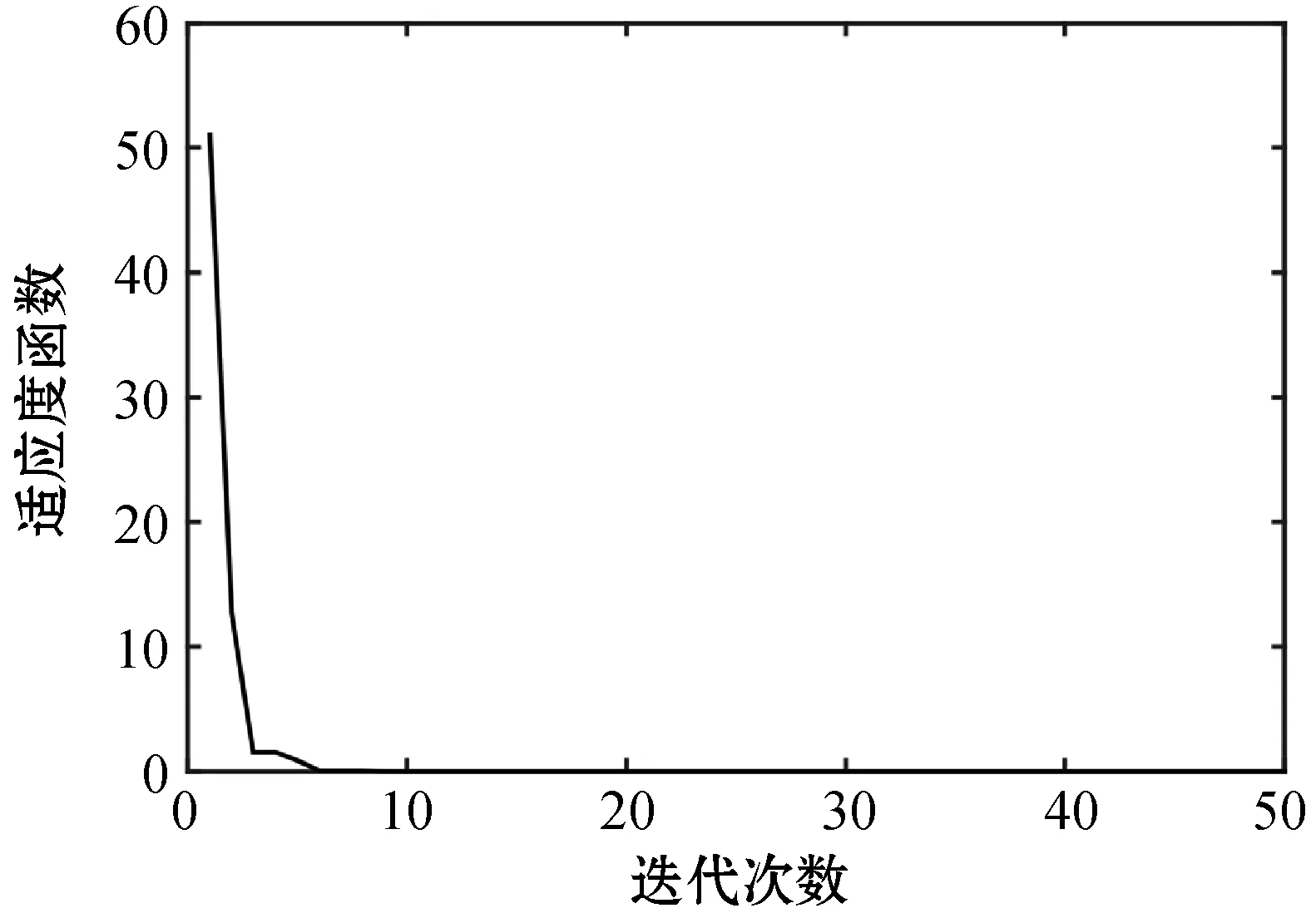
图10 连续搅拌反应釜辨识适应度演化曲线
可以看出,随着迭代次数的增加,连续搅拌反应釜辨识的参数估计误差越来越小,而且适应度演化曲线趋于0,说明辨识算法是有效的。
6 结 语
本文提出改进DE算法来辨识Hammerstein CARMA系统,并且与RLS算法、基本DE算法和PSO进行对比。仿真结果表明,改进DE算法相对于RLS算法、基本DE算法和PSO可以更有效地辨识Hammerstein CARMA系统的参数,其参数估计精度更高,收敛速度更快。将改进DE算法应用在连续搅拌反应釜中,取得了较好的应用效果。

