基于VMD-DenseNet的短期电力负荷预测
余 珊 温 蜜 顾春华 陈禹帆
1(上海电力大学计算机科学与技术学院 上海 201306) 2(上海理工大学光电信息与计算机工程学院 上海 200093)
0 引 言
短期电力负荷预测对于电力系统的能源管理、可靠性分析、安全风险评估和降低用电成本等方面都具有重要的意义[1]。随着电力系统的不断发展和日益精细化的管理需求,准确的短期负荷预测已经变得越来越重要和具有技术挑战性。电力负荷的变化主要受社会、经济及环境等多方面的影响,因此,基于电力负荷复杂的变化特性,研究新的短期负荷预测方法以提取数据中的潜在特征,对于进一步提升预测精度有着重要的意义。
短期负荷预测的研究方法主要包括时间序列模型和机器学习方法等。时间序列模型主要以线性模型为基础,考虑了数据的时序性关系,但对于温度、天气类型等非线性特征难以捕捉[2]。机器学习方法主要有支持向量机[3](Support Vector Machines,SVM)和神经网络[4]算法等。SVM方法在处理小样本和高维数据集上具有优势,但在大规模样本下训练效率较低。
随着深度学习的迅速发展,许多研究者将神经网络算法运用于时间序列预测领域[5-6]。文献[7]基于深度神经网络(Deep Neural Networks,DNN)对工业园区负荷进行预测,很好地捕捉了输入数据的非线性特征,但当网络层数较多时,模型易导致参数数量膨胀和产生梯度消失问题。文献[8]建立了电力市场中基于长短期记忆网络(Long Short-Term Memory,LSTM)的短期负荷进行预测模型,很好地捕捉输入数据长期和短期的相关特征。然而,当输入序列较长时,LSTM会出现丢失历史关键信息的问题,且其不能进行并行计算,影响了模型的准确率和效率。卷积神经网络(Convolutional Neural Network,CNN)具有提取数据细节特征的优势,因此逐步运用于负荷预测领域[10-11]。为加强CNN的表达能力,一些改进模型如Inception、ResNet和密集连接卷积网络[9](Densely Connected Convolutional Network,DenseNet)被提出,在计算机视觉领域表现出卓越的性能,但较少运用于负荷预测领域。DenseNet采用独特的密集连接方式以更好地实现特征重用,有效解决深层神经网络易产生的梯度消失问题,提升模型的准确性。文献[12]通过构建二维输入特征图,将DenseNet运用于日前光伏出力预测,取得了较为理想的效果。
由于信号的非平稳性,单一预测模型通常不能取得令人满意的预测结果,因此基于信号分解和数据挖掘等方法与预测模型相结合的组合预测模型得到广泛地运用[13]。一些实验结果表明,信号分解技术如小波分解[14]和经验模式分解[15](Empirical Mode Decomposition,EMD),给模型的预测精度带来了显著的改进。相比于小波分解,EMD不受小波基函数的选择、分解层数等影响,它可以用于分析非线性、非平稳的信号序列,具有良好的时频聚焦性。但EMD存在模态混叠现象,且不能自主选择分解的模态函数个数,因此建模复杂度较高。
为提升短期电力负荷的预测精度,本文针对上述文献中存在的问题,提出了一种基于VMD-DenseNet的短期电力负荷预测方法。为了减少预测模型的训练难度并使模型顺利收敛,利用变分模态分解(Variational Mode Decomposition,VMD)方法分解原始负荷,通过VMD识别输入负荷序列中的潜在特征,将数据分解为三个频率各异的分量:趋势分量、细节分量和随机分量。对各分量和特征变量进行最大信息系数(Maximal Information Coefficient,MIC)相关性分析,选取影响较大的特征变量作为输入变量。采用一维DenseNet网络模型对各分量输入序列进行建模,以加强特征重用,更加充分地提取数据中隐藏的丰富特征。以欧洲某电网的负荷数据集为算例进行实验,对负荷进行提前1 h和提前6 h预测,所提出的模型相比其他模型具有更高的预测精度。
1 相关原理
1.1 最大信息系数
MIC[16]是2011年提出的一种变量相关性分析方法,常被用于输入变量的选择。该方法能较好地衡量两个变量之间线性或非线性的关联程度。具体描述如下:
设X,Y为数据集D中的两个随机变量,其中X={xi,i=1,2,…,n},Y={yi,i=1,2,…,n},n为样本数。定义X与Y之间的互信息为:
式中:p(x,y)为X和Y的联合概率密度;p(x)和p(y)分别为X和Y的边缘概率密度。
将数据集D中两个随机变量X和Y离散在二维空间中,并把二维空间沿x和y方向划分,形成一个网格G=(a,b),a、b分别为在x、y方向上划分的网格数,然后查看两个变量组成的散点在网格中的分布情况,则最大互信息可定义为:
式中:D|G为数据集D在网格G下的划分。X与Y的最大信息系数为:
式中:n为样本集的数量,B为变量,通常情况下,B=n0.6。MIC将不同划分下得到的最大互信息值归一化,取值范围为[0,1]。若某两个变量具有较高的MIC值,表明两个变量之间的相关性较强,相反,较低的MIC值则表明两者相关性较弱。
1.2 变分模态分解
VMD是一种新的信号分解方法,它可以有效地识别非线性和非平稳信号中的周期性特征,并且能够避免产生EMD存在的端点效应和模态混叠问题,对于噪声具有较强的鲁棒性,因此可获得较为理想的信号分析结果,在信号分解中表现出良好的性能[17]。该方法可以人为设置本征模态函数的个数k,通过合理地设置k值,可以降低模型的建模复杂度。
VMD方法主要通过获取最优解的方式来自适应地将输入序列f(t)分解为k个不同频率的模态函数uk,并且通过不断地确定每个模态函数的中心频率和带宽,以使估计带宽的总和达到最小值,从而获得最优的分解结果。具体步骤如下:
1) 通过Hilbert变换可以获得每个模态函数uk的有限边际谱,预估每个模态函数相应的中心频率,调制其频谱到模态函数相应的基频带,然后通过H1高斯平滑法估计每个模态函数的带宽。带约束条件的变分问题的目标函数如下:
式中:{uk}={u1,u2,…,uk}和{ωk}={ω1,ω2,…,ωk}是模态函数集和中心频率集;δ(t)是单位脉冲函数。
2) 通过引入二次惩罚因子α和拉格朗日算子λ(t)这两个参数,以消除约束变分问题的约束条件,使其变为非约束性变分问题,扩展的Lagrange函数表达式如下:
3) 通过采用交替方向乘子法(ADMM)更新uk和ωk,寻求式(5)的鞍点,以解决原始最小化问题。最终,求解得到uk和ωk的表达式如式(6)和式(7)所示。
4) 依据式(8)更新Lagrange惩罚算子:
式中:τ为更新参数。
5) 判断是否满足迭代结束条件,若满足,则根据模态函数个数k得到相应的分解子序列。
1.3 密集连接卷积网络
一般来说,更深的网络可以带来更高的预测精度,但对于深度神经网络而言,随着网络深度的进一步加深,梯度消失问题会愈加明显[18]。
DenseNet提出了一个密集连接机制:通过添加多个跳跃连接,将每个层与之前所有层的输入进行拼接,作为其额外的输入,从而将所有层都相互连接起来。一个密集块的结构图如图1所示。
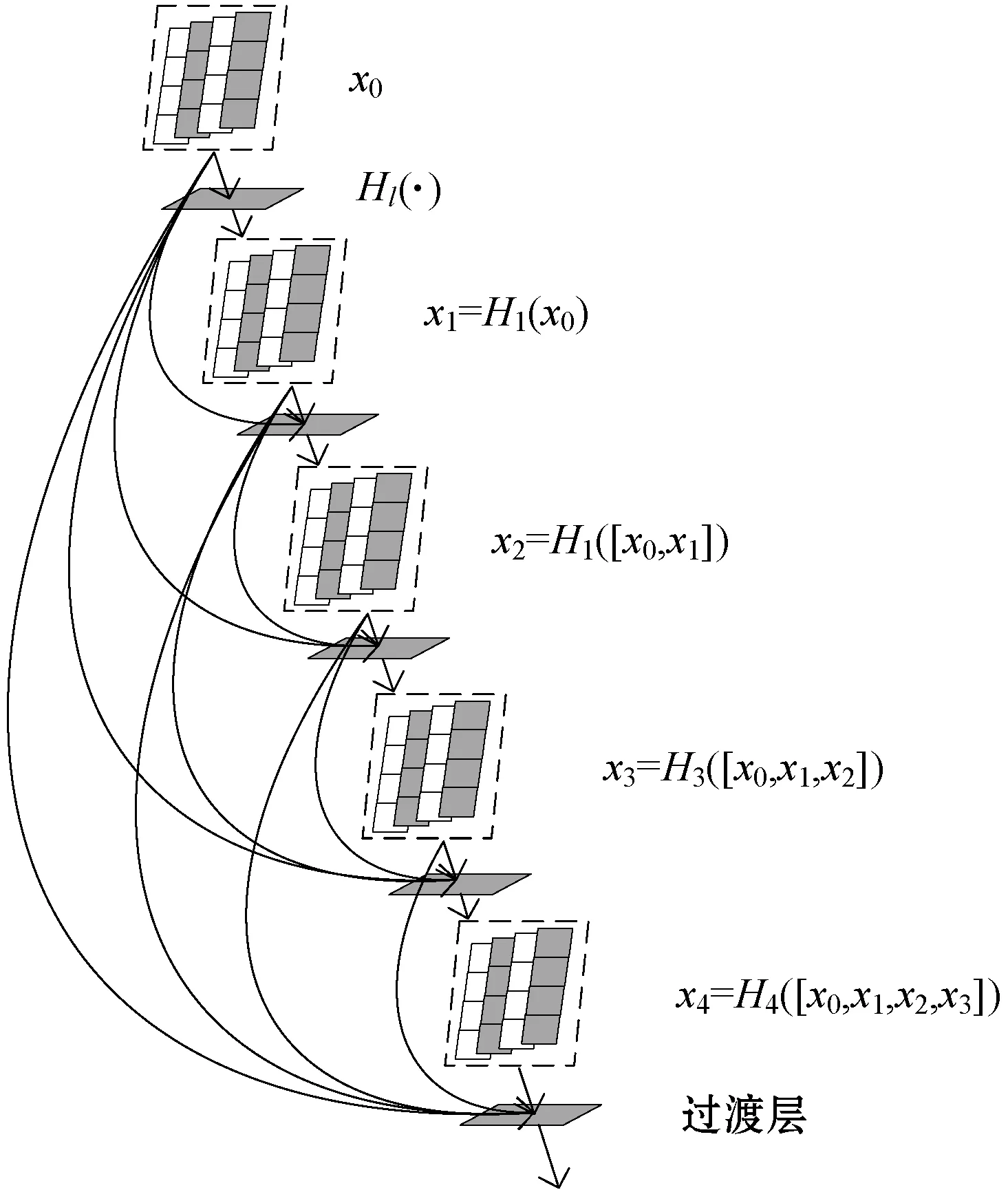
图1 密集块结构图
对于一个l层的网络,传统的CNN每层仅有1个输入,连接个数共l个。而DenseNet第l层网络有l个输入,连接个数共l(l+1)/2个,网络在l层的输出为:
xl=Hl([x0,x1,…,xl-1])
(9)
式中:[x0,x1,…,xl-1]表示第0,1,…,l-1层的输出在特征维度上的拼接,Hl(·)代表第l层包含卷积在内的非线性转化复合函数。拼接操作将卷积层提取的特征信息进行融合,使得网络中每一层的输入均为该层前面所有层输出特征图的并集,且当前层的特征图也直接传递给之后的所有层作为输入,从而增加数据训练时的原始特征。
DenseNet网络可以由n个密集块和n-1个过渡层组成,其密集块独特的密集连接机制,最大程度地增加了网络中各层之间的信息流,从而有助于神经网络模型训练过程中梯度的反向传播,使得训练深层网络变得更加容易;过渡层位于两个密集块之间,用以减少特征输出的维度。相比于其他深层神经网络,DenseNet不仅缓解了梯度消失问题,还增强了神经网络中各层之间特征的传递,通过特征的连接来实现特征重用,更有效地利用了特征,使模型在参数和计算成本更少的情形下,达到更优的性能。
2 模型构建
本文主要关注对未来某时刻的电力负荷进行预测,通过获取负荷序列中蕴含的丰富特征,利用深层神经网络模型加强对数据中的特征的提取,以获得较高的预测精度。因此,提出一种基于VMD-DenseNet的短期负荷预测模型(以下简称VDSN),模型结构如图2所示。首先采用VMD分解方法将原始负荷序列分解为3个分量,并为各分量选择合适的特征变量;其次,采用一维DenseNet预测模型预测各分量负荷;最后,重构各分量预测结果得到最终的负荷预测值。

图2 VDSN短期负荷预测模型
2.1 VMD分解原始负荷序列及各分量变量选择
通过VMD分解方法可以将原始输入负荷序列分解k个特征互异的模态函数,但过多的模态函数个数会增加预测模型的复杂度和训练时间,因此本文选取k=3,得到3个频率互不相同的分量。
以欧洲某电网的负荷数据为例,原始负荷及其分解得到的三个分量曲线图如图3所示。根据各分量曲线图和电力负荷数据的趋势性、周期性和随机性等特点,定义三个分量分别为趋势分量、细节分量和随机分量。其中,趋势分量代表负荷数据整体变化的趋势性,细节分量具有一定的周期性,幅度受节假日、时间类型等因素的影响,随机分量由经济因素、用户的用电行为等变化而引起,具有较大的波动性和不确定性。通过使用VMD,识别了隐藏在原始负荷序列中的潜在特征,并获得分解后的各分量序列,与原始信号相比,这三个分量清晰地体现了电力负荷的变化性特点。

图3 VMD分解原始负荷序列结果图
输入变量是影响短期负荷的重要因素,由于影响因素的差异性,通常会选择与负荷序列相关性较强的因素作为特征变量,构建输入变量集合。因此对由VMD分解出的各分量进行影响因素相关性分析,针对历史负荷、温度、天气类型(晴、多云和雨)、时间类型(小时、星期、月份、季节和节假日)等数据,通过MIC相关性分析方法筛选出与各分量具有较强相关性的影响因素,作为各变量的输入特征变量集合,具体参数见表1。

表1 各分量输入变量选择结果
2.2 一维DenseNet预测模型结构
二维CNN善于处理较为复杂的信息和结构数据,因此多用于计算机视觉、图像处理等领域。而一维CNN能够较好地用于序列类数据的分析处理,比如电力负荷时间序列数据。为了更加充分地利用一维时间序列中的特征,以及准确地预测未来某时刻的负荷,文中采用一维DenseNet进行负荷预测。
对各分量的输入序列,利用DenseNet模型有效地提取数据中蕴含的趋势性、周期性和随机性等特征,最大限度地保留这些特征对负荷序列的影响,学习这些特征与负荷之间的关系,提升预测精度。模型采用三维数据进行输入,且模型中的卷积层均采用一维卷积,具体层结构如图4所示。
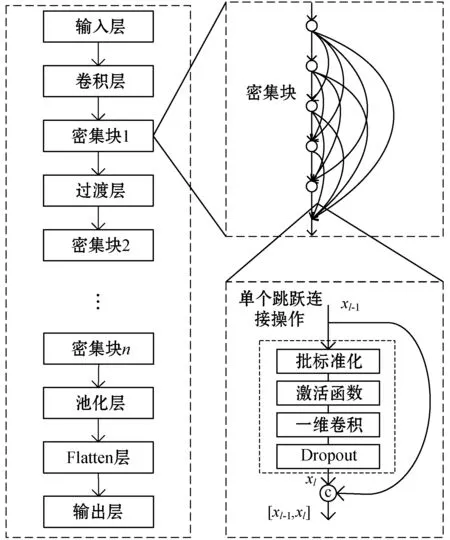
图4 一维DenseNet模型结构图
(1) 输入层。采用滑动窗口方式输入数据,设置窗口大小为24,时间步长为1,假设当前分量的输入变量个数为n,则模型输入为24×n,其中n维特征向量分别代表当前时刻的负荷值及由MIC筛选出的历史负荷、天气数据和时间类型数据。
(2) 卷积层。对输入数据进行一维卷积化操作以初步提取数据中隐藏的细节特征,卷积核个数为128。
(3) 密集块。首先,将密集块中的复合函数Hl(·)设计为一个组合操作,包括批标准化、ReLU激活函数、一维卷积层及Dropout正则化。其中,批标准化用于降低样本间的差异,对每一层的输入作标准化处理,激活函数用于提升神经网络模型的非线性表达能力,卷积层用于提取数据中蕴含的丰富特征。另外,在Hl(·)中添加Dropout层,以防止模型过拟合,并且增强模型的抗噪能力。
将卷积后的数据输入到密集块中,模型中共包含n个密集块,每个密集块均采用密集连接,并且包含4个卷积层。其中第一个卷积层选择大小为1的卷积核,以减少输入特征的数量,提升计算效率。其余卷积层均选择大小为3的卷积核,以对数据中的特征进行提取,所有卷积层的卷积核数目均为8。
(4) 过渡层。为连接两个相邻的密集块并减少特征数量,在每两个密集块之间加入一个大小为1,卷积核数为64的卷积层。
(5) 池化层。对密集连接后的特征进行尺寸为5的最大池化操作,以降低网络复杂度,减小输出维度大小。
(6) Flatten层。将二维向量数组进行切片,形成一维向量数组,作为全局特征提取。
(7) 输出层。通过全连接层对数据进行回归输出,得到预测后的负荷数据。
2.3 各分量预测结果重构
将由趋势分量、细节分量和随机分量三个分量预测得到的预测分量Pi(i=1,2,3)进行叠加式重构,如式(10)所示,P为最终的负荷预测结果,然后将其与真实负荷值进行对比。
3 算例分析
3.1 实验数据集
采用欧洲某电网2016年的负荷数据集作为研究对象,数据来源于欧洲互联电网(ENTSO-E)。选取2016年1月至2016年11月的数据作为训练集,2016年12月的数据作为测试集,数据时间间隔为1小时。同时收集当地气象站采集的温度、天气类型数据及当地节假日等数据。
图5为某一周的负荷数据曲线图,起始时刻为周一的零点。可以看出,日负荷值在白天达到峰值,在夜间达到低谷,且用电高峰期具有一定的波动性。在一周时间内,负荷具有较强的周期性,并且幅值会根据日期类型等特点而发生不同程度的变化。在工作日,负荷幅值较大;在非工作日,负荷幅值相比于工作日明显减小。
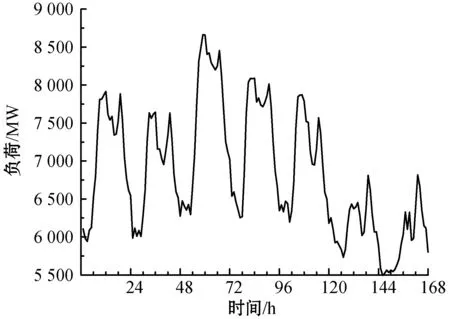
图5 某一周的负荷曲线图
3.2 数据预处理及评价指标
为便于模型的训练,首先对所有数据集进行数据预处理,将标志性数据进行编码处理,并对选择的历史输入数据进行归一化处理,将数据映射到[0,1]范围内。公式如下:
式中:xmin、xmax是各输入变量的最小值和最大值,xi是当前变量的输入值。
为较好地评估模型的性能,使用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)两种性能评价指标对预测结果进行分析。MAPE和RMSE的计算公式分别为:

3.3 实验对比分析
为验证文中所提出的VDSN模型的性能,本文分别与基于DNN、LSTM、DenseNet、VMD-DNN和EMD-LSTM的五种预测模型进行实验对比。模型均可以在不同的时间范围内对未来负荷进行点预测,包括提前1 h和提前6 h。实验均在装有GeForce RTX 2080Ti GPU的服务器上进行,模型开发基于Python和Keras框架。
实验中DenseNet采用3个密集块,相对应的,DNN和LSTM分别设置为效果较好的3层结构,隐藏层神经元个数分别设置为128、64、64,并且在每个隐藏层中加入0.2的Dropout率以防止过拟合,所有模型采用早停法进行实验。
表2为6种不同模型对负荷进行提前1 h预测和提前6 h预测的连续一周(12月12日—12月18日)的预测结果对比。可以看出,无论是工作日(12月12日—12月16日)还是非工作日12月17日—12月18日),VDSN模型的每日预测误差MAPE和RMSE值相对于其他模型基本都较小,表明该模型的预测精度较为理想,预测精度较高。

表2 12月12日—12月18日提前1 h负荷预测的结果比较
为探究模型的通用性,本文对提前1 h预测和提前6 h预测两种不同尺度的预测结果进行了分析。图6为提前1 h预测的某日结果对比图,图7为提前6 h预测的某日结果对比图。
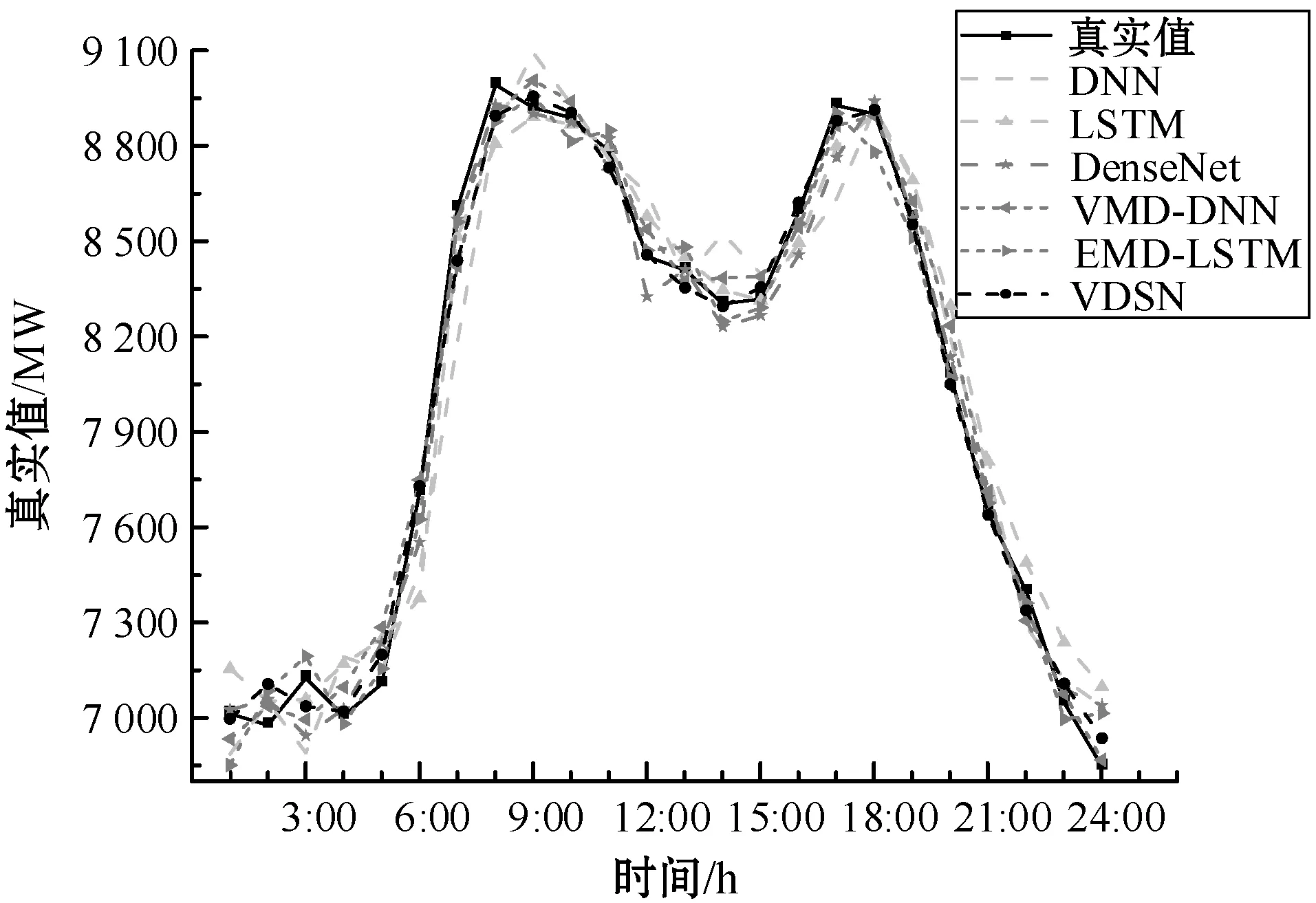
图6 提前1 h预测的某日结果对比

图7 提前6 h预测的某日结果对比
由图6和图7可以看出,VDSN模型的预测结果更加接近真实值,因此预测精度最高,其他模型预测结果均次于该模型。对于单个模型,DNN和LSTM的预测效果相比DenseNet模型预测精度要差,对于组合模型,VMD-DNN和EMD-LSTM模型的预测误差相比于VDSN模型都较大。特别地,对于提前6 h预测,单个模型的预测精度明显低于组合模型的预测精度,模型稳定性相比提前1 h预测较差。
表3为两种不同时间尺度的12月份整体情况对比。由表3的分析结果可知,提前1 h的预测精度整体优于提前6 h的预测精度。从模型预测角度来说,加入VMD或EMD的组合模型预测效果比单一预测模型得到明显提升。另外,LSTM和DNN模型在预测不同时间尺度的负荷数据时各有优缺点,但两者预测精度都次于DenseNet模型。在两种不同的预测时间尺度下,本文提出的组合模型VDSN都具有更高的预测精度。对于提前1 h预测,VDSN模型相比于VMD-DNN、EMD-LSTM模型MAPE值分别提升了17.82%和15.31%,RMSE值分别提升了15.37%和21.90%;对于提前6 h预测,VDSN模型相比于VMD-DNN、EMD-LSTM模型MAPE值分别提升了13.49%和29.55%,RMSE值分别提升了13.23%和34.25%。综上,基于VMD和DenseNet的混合模型VDSN提高了特征的利用率,能够获得更好的预测效果,提升了预测精度。
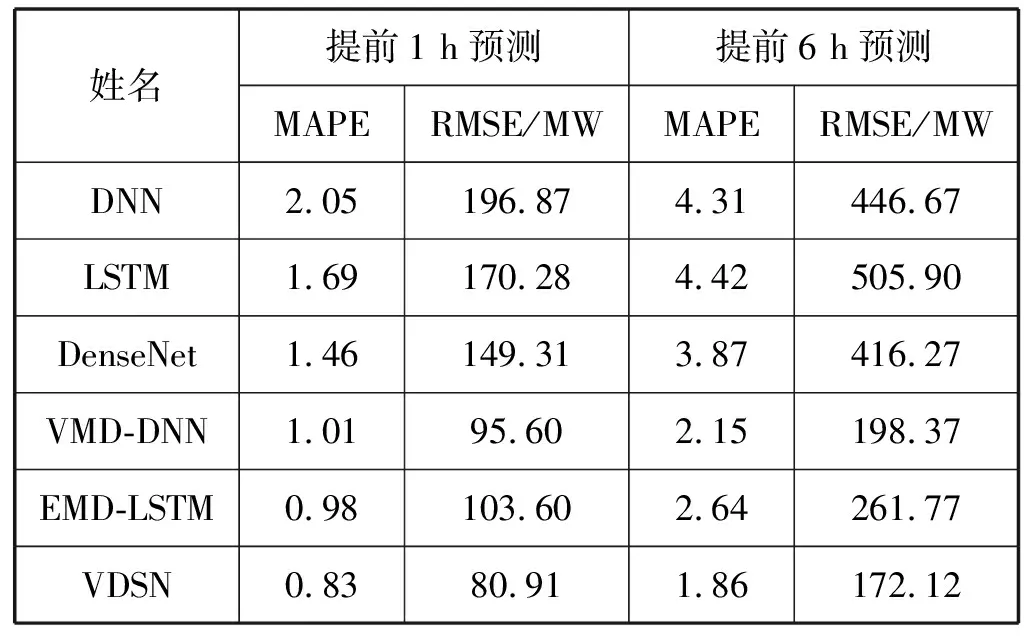
表3 两种不同时间尺度的12月份预测精度比较
4 结 语
本文结合人工智能领域热点研究方向,提出了一种基于VMD-DenseNet的方法对短期电力负荷进行预测。VMD方法能够避免发生模态混叠问题,获得较好的负荷序列分解效果,掌握负荷的趋势性、周期性和随机性等特点。利用MIC对每个分量的输入变量(历史负荷、环境和时间特性等)进行相关性分析,加强了重要特征对模型的影响并降低了数据冗余。借助DenseNet复杂的网络结构进行深度负荷预测,既有效地避免了梯度消失问题,也加强了对各分量数据的特征提取。实验结果表明所提出的模型,能够获得更高的预测精度,具有更优的性能。
未来的研究中,我们考虑进一步将DenseNet网络运用于负荷预测领域,比如概率预测、多尺度预测等,并且通过优化其连接方式,加强其特征提取能力,提升模型的普适性。

