密集结构改进双通道神经网络的遥感图像配准

王东振 陈 颖 李文举 李绩鹏

(上海应用技术大学计算机科学与信息工程学院 上海 201418)

0 引 言

遥感图像是指由航空器或卫星上成像系统获得的具有地面目标特征的图像,遥感图像配准是寻找在不同的时间或不同的传感器捕获的图像对间最佳对齐的过程,目前遥感图像配准技术已被广泛应用于地面目标识别、城市和地理变化评价等军事和民用领域。

目前图像配准两类主流的趋势方法是基于区域或特征的算法。基于区域的配准算法,如Rosenfeld等[1]提出了交叉相关的概念,此类方法是以模板的形式来比较灰度区域间的相似性程度,从而判断配准位置。基于特征的算法一般采用表示高级信息的特征描述符来实现配准,因此预期在图像外观发生变化的配准中更可取。所以在此对现有的一些基于特征的方法进行了介绍和讨论。由Lowe等[2-3]提出的SIFT算法运用到图像配准中所得到的配准结果具有较好的鲁棒性,并且该算法对于图像的旋转、缩放、尺度变换都具有良好的不变性[4],因此现有的基于特征的图像配准方法大部分都采用SIFT或其改进算法来检测特征点。然而若待配准的图像对之间在外观上存在显著地貌上的差异,采用传统算法检测出的特征点可能存在较多的外点或检测到的特征点数量不足,这些问题则限制了传统算法在具有显著地貌差异的遥感图像配准中的应用。

近年来,在计算机视觉等领域对深度学习的运用越来越广泛起来。针对传统算法检测特征点不足问题,由Hamester等[5]在2015年提出了一种新的网络架构即双通道卷积神经网络,其中的一个通道设计为卷积式自动编码器(CAE),另外一个为CNN的通道将保持不变,最后将来自两个不同通道所得到的图像信息融合汇聚在同一个全连接层中,该算法实现了图像多尺度特征的融合。Liu等[6]提出的双通道卷积神经网络(CNN),用于SAR图像变化检测,这个网络模型包含两个并行的CNN结构,可以从两个不同时间段的SAR图像中提取特征,丰富了网络的提取特征。Gu等[7]提出了由SCNN(单通道卷积神经网络)和SBNN(单通道二值神经网络)组成的双通道卷积神经网络,该算法实现了不同通道的卷积神经网络对于图像提取的局部与全局特征的融合,对于之后的图像处理如(目标检测或图像配准)都会有较好的结果。Bai等[8]基于以往的双通道卷积神经网络架构的基础上,参考稠密网络结构对双通道卷积神经网络各个卷积层的连接方式做出了改变,由之前的顺序连接修改为跨连接,增加了特征的重利用率,减少了局部的特征缺失。针对外点问题,提出了一种鲁棒点集匹配算法是由Myronenko等[9]提出的一致性点漂移算法(Coherent Point Drift,CPD),该算法对于由于出格点或缺失点等问题所得出的非刚体的配准结果具有较强的鲁棒性。

针对传统算法检测的特征点不足或具有较多无效的特征点的问题,本文提出对输入的图像采用密集结构改进的双通道卷积神经网络进行特征提取,生成各自的特征点。然后利用粒子群算法对CPD算法进行改进,对生成的特征点集进行匹配,从而实现图像配准。通过实验数据对比表明,本文算法的配准精度比传统算法的更高。

1 本文配准系统框架

1.1 网络模型

为了实现图像配准,本文提出了基于双通道卷积神经网络的模型架构,具体的功能结构图如图1所示:

图1 系统功能框架模型图

(1) 将大小为224×224参考图像与待配准图像输入到由VGG16和VGG19共同组成的特征提取网络。

(2) 经过特征提取网络的两个卷积块后,进入VGG16和VGG19的第3个卷积块的卷积层,输出维度为256,卷积核大小为3×3,步长为1,填充的方式采用“same”,类似操作再重复2-3次,进入VGG16和VGG19的第3个卷积块的池化层,输出维度同样为256,步长为2,采用最大池化,填充方式同样采用“same”。

(3) 以此类推,分别进入VGG16和VGG19的第4和第5个卷积块的卷积层和池化层,除了输出维度均修改成512,卷积层和池化层中各个参数的设置均与步骤2中的相同。

(4) 将参考图像和待配准图像在不同通道中的后3个卷积块得到的相应的特征图大小28×28×256、14×14×512、7×7×512进行特征融合,并生成相应的特征点集。

(5) 通过使用随机优化算法改进的CPD,来增加确定参数的可靠的特征点的数量,从而提高特征匹配的精度。最后待配准图像根据特征匹配得到的仿射变换参数完成配准。

1.2 密集结构改进双通道网络

1.2.1双通道卷积神经网络

对于传统采用单通道的卷积神经网络来说,随着网络层数深度的增加,会造成提取的图像局部特征的缺失,从而影响最终的配准结果。本文提出用VGG16和VGG19构成双通道卷积神经网络完成对图像特征的提取,通过对VGG16包含的第三、四、五卷积块提取的图像特征和VGG19相对应的卷积块提取的特征进行特征融合,实现了网络提取特征多尺度的融合,丰富了网络提取的特征,最终图像配准的效果也越好。

VGG16是其中的一个通道,它所包含的网络结构和部分参数如下所示:VGG16网络总共包含五个卷积块blocki(i=1,2,3,4,5),每个卷积块中包含若干个卷积层和1个池化层。其中,前两个的卷积块(称为卷积块A)的结构相同而后3个卷积块(称为卷积块B)的结构也相同,它们之间的连接方式采用依次顺序连接。blockiconvi和pooli(i=1,2,3,4,5)分别代表VGG16网络中不同卷积块中所包含卷积层和池化层。其中,各个卷积层的卷积核的大小为3×3,步长为1×1,各个卷积块中卷积核的个数分别为64、128、256、512、512。池化层的步长2×2,池化方式采用最大池化。

VGG19网络是双通道网络模型的另一个通道,它的网络结构与VGG16区别在于VGG19网络模型后三个卷积块中比VGG16网络各多了1个卷积层。其中,各个卷积层的卷积核的大小、步长、各个卷积块卷积核的个数、池化层的步长等参数均与VGG16网络设置相同,池化方式也采用最大池化。

双通道卷积网络由Hamester等提出,它的基本思想是特征融合。传统的单通道卷积神经网络直接把第n层最后一层的输出用来完成对于图像的配准、目标识别和场景分类等。假设双通道卷积神经网络中的两个网络通道中各包含N层,其中各个通道中的每一层分别都包含一个非线性变换Hn=(*)和非线性变换Gn=(*),n表示网络中的第n层,Hn=(*)和Gn=(*)代表各种网络作用,如卷积或池化、归一化。将第n层的输出记为Xn,最终的输出记为Yn,双通道卷积神经网络实现了不同通道的多尺度的特征的融合,相关公式如下:

Yn=Hn(Xn-1)+Gn(Xn-1)

(1)

双通道卷积神经网络利用对不同通道对图像提取的特征进行融合,使最终得到的图像特征更加具有多样性。本文的双通道网络模型是由改进后的VGG16和VGG19两个通道组成的网络架构,具体结构如图2所示。可以看出,VGG16和VGG19网络都是由2个卷积块A和3个卷积块B组成。

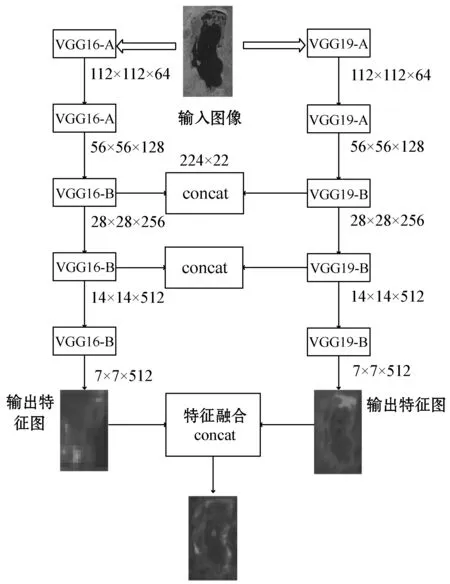
图2 双通道网络结构示意图

使用不同的特征融合网络结构会得到不同的融合结果,原因在于不同的网络结构的特征提取能力不同。一般的双通道网络模型均采用最后一层融合后的图像特征做图像的配准、识别或分类等,但仅采用最后一层提取的图像特征会造成网络浅层提取的部分局部特征没有得到充分的利用。由于两个VGG网络相应层采用的卷积核大小及个数均相同,有利于它们之后的特征融合。本文采用将各个通道后3层池化层融合后的特征作为最终的输出,其建立了不同通道之间的紧密连接,相关公式如下:

A3=H10(X9)+G11(Z10)

B4=H14(X13)+G16(Z15)

C5=H18(X17)+G21(Z20)

(2)

式中:A3、B4、C5分别代表双通道网络模型中相应的第3、4和5卷积块融合后的特征输出;H(*)和G(*)分别代表VGG16和VGG19网络中各个层所包含的非线性变换,如卷积和池化等;Xi(i=1,2,…,18)和Zj(j=1,2,…,21)分别表示VGG16和VGG19网络中第i和j层的输出。

使用Python、TensorFlow完成VGG16和VGG19提取的特征融合,代码如下:

def register(self,IX,IY):

#定义图像配准函数,输入为参考图像与待配准图像

# set parameters

tolerance=self.tolerance

#允许容忍的最小误差

freq=self.freq

#用于记录节点的使用频率

epsilon=self.epsilon

#被定义为最小的数

omega=self.omega

#加权平均数中的权值

beta=self.beta#

lambd=self.lambd#

# resize image

Xscale=1.0*np.array(IX.shape[:2])/self.shape

#计算参考图像与图像缩放后的权重比值大小

Yscale=1.0*np.array(IY.shape[:2])/self.shape

#计算待配准图像与图像缩放后的权重比值大小

IX=cv2.resize(IX,(self.height,self.width))

#将参考图像IX的宽和高缩到已经给出的参数大小

IY=cv2.resize(IY,(self.height,self.width))

#将待配准图像IY的宽和高同样缩放到已经给出的参数大小

# CNN feature

# propagate the images through VGG16

IX=np.expand_dims(IX,axis=0)

#在IX的第一个

#维度上增加一个新的维度,以使数组维度相匹配

IY=np.expand_dims(IY,axis=0)

#在IY的第一个

#维度上增加一个新的维度,以使数组维度相匹配

cnn_input=np.concatenate((IX,IY),axis=0)

#能够一次完成多个数组的拼接,即对参考图像和

#待配准图像的特征进行融合

with tf.Session() as sess:

#使用with tf.Session()创建

#上下文(Context)来执行,当上下文退出时自动释放

feed_dict={self.cnnph:cnn_input}

#用feed_dict以字典的方式填充占位

D1,D2,D3=sess.run([

self.vgg.pool3+self.vgg1.pool3,self.vgg.pool4+self.vgg1.pool4,self.vgg.pool5+self.vgg1.pool5_1],feed_dict=feed_dict)

#分别将vgg和vgg1对应的VGG16和VGG19后

#3个卷积块提取的特征进行融合

图2中还给出若输入的图像为224×224,则各个通道中各个卷积块相应的输出特征图的大小。

1.2.2密集网络

密集连接卷积网络由Huang等提出,它的基本思想是采用“全跨链”的连接方式。后面每一层的输入是其之前所有层所得到的特征图的融合,其建立了高层与之前所有层的紧密连接。

传统的神经网络需要将第n层的输出作为结果输入到下一层第n+1层。假设神经网络总共包含N层,其中网络中的每一层都包含一个非线性变换Hn=(*),n表示网络中的第n层。Hn=(*)代表各种网络作用,如卷积或池化,归一化。将第n层的输出记为Xn。那么传统网络的转换就可以表示为:

Xn=Hn(Xn-1)

(3)

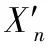
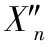
式中:[X0,X1,…,Xn]为第0,1,…,n-1层网络层输出的特征图。密集连接网络通过增强提取特征的传播和重利用,能够有效地解决由于网络深度增加造成梯度消失的问题。

1.2.3对Vgg网络模块的优化

VGG16是由两种类型的卷积块A和卷积块B组成,图3和图4分别为密集网络改进VGG16单个卷积块的结构示意图。改进后的卷积块仍然由若干个卷积层和一个池化层组成,实现对图像的特征提取。但是其中前面每一个卷积块单元最后的输出结果都与下一个卷积块单元中的多个卷积层的输出建立连接,增加了信息的重复利用率。

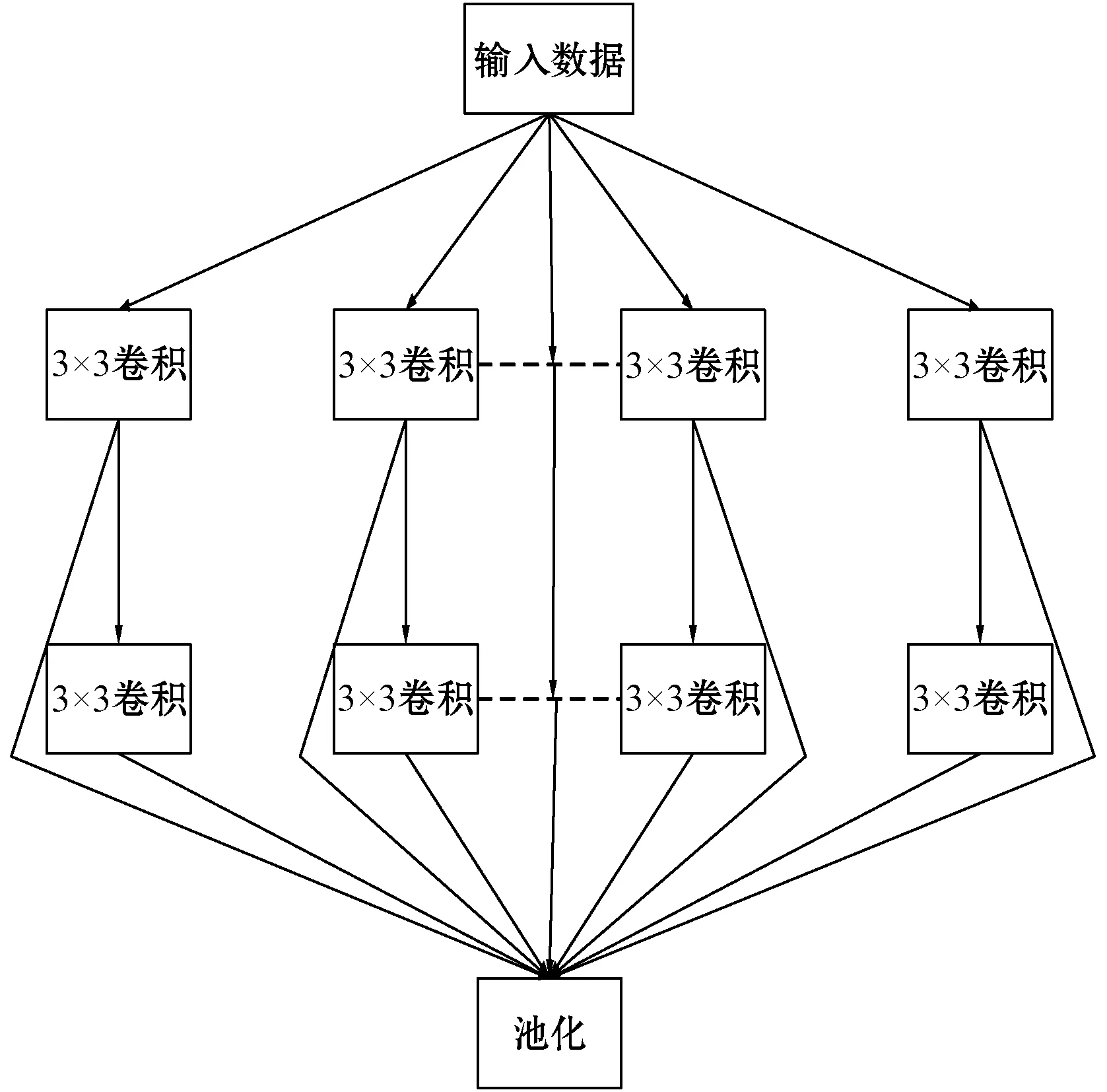
图3 VGG16单个卷积块A的连接示意图

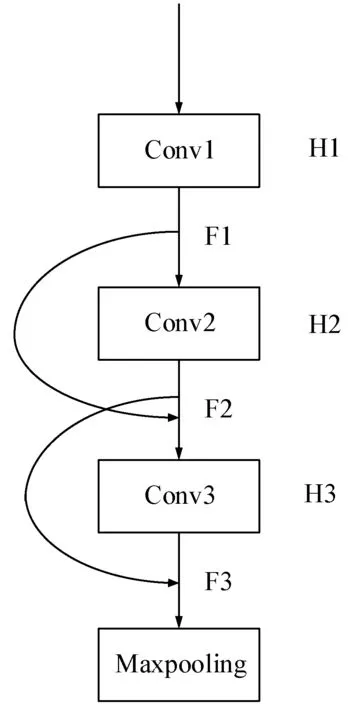
图4 VGG16单个卷积块B的连接示意图

图3为密集网络改进后的卷积块A模块,包括2个卷积分支(从上到下依次为第1和第2卷积分支)和一个池化分支,2个卷积分支的卷积核大小和个数均为3×3和64(图中虚线部分表示省略的卷积核)。可以看出,在池化分支部分使用密集网络重复利用第一卷积分支所提取到的图像特征,增加了特征的利用率。

图4为优化后的卷积块B模块,采用部分跨链的连接方式将卷积块中第一层与第二层的特征图F1、F2结合作为第三层的输入F3,并将第二、三层得到的特征图再次结合作为池化层的输入F4,最后对剩余的卷积块B做同样的处理。这样使网络能充分利用每一层特征图的信息,实现提取特征的重复利用,同时这些特征图的结合并没有增加网络的复杂度,相关公式如下:

F1=H(x0)=x1

F2=H(x1)=x2

F3=H(x0)+H(x1)

F4=H(x1)+H(F3)=

H(x1)+H(H(x0)+H(x1))

(6)

式中:Fi(i=1,2,3,4)分别代表第i个卷积层所得到的特征图的输入或输出,H(*)代表该卷积层的非线性操作,包括卷积或归一化等。xi(i=0,1,2,3)代表第i个卷积层的输出(i=0时表示上一个卷积块的输出)。

使用Python、TensorFlow完成VGG16结构的构建和改进,改进VGG16结构代码如下:

# 开始构建卷积层

# vgg16的网络结构

# 第一层:2个卷积层1个pooling层

# 第二层:2个卷积层1个pooling层

# 第三层:3个卷积层1个pooling层

# 第四层:3个卷积层1个pooling层

# 第五层:3个卷积层1个pooling层

# 这些变量名称不能乱取,必须要和vgg16模型保持一致

# 另外,将这些卷积层用self.的形式,方便以后取用方便

self.conv1_1=self.conv_layer(x_bgr,′conv1_1′)

#第一个卷积块的第一个卷积层,输入为原始图片,

#输出为卷积操作后的特征图F1。

self.conv1_2=self.conv_layer(self.conv1_1,′conv1_2′)

#第一个卷积块的第二个卷积层,输入为特征图F1,

#输出为卷积操作后的特征图F2。

self.pool1=self.pooling_layer(self.conv1_2+self.conv1_1,′pool1′)

#第一个卷积块的池化层,输入为F1和F2

#融合后的特征,输出为池化操作后的特征图F3。

self.conv3_1=self.conv_layer(self.pool2,′conv3_1′)

#第三个卷积块的第一个卷积层,输入特征图F6,

#输出为卷积操作后的特征图F7。

self.conv3_2=self.conv_layer(self.conv3_1,′conv3_2′)

#第三个卷积块的第二个卷积层,输入为特征图F7,

#输出为卷积操作后的特征图F8。

self.conv3_3=self.conv_layer(self.conv3_2+self.conv3_1,′conv3_3′)

#第三个卷积块的第三个卷积层,输入为

#F7和F8融合后的特征,输出为卷积操作后的特征图F9。

self.pool3=self.pooling_layer(self.conv3_3+self.conv3_2,′pool3′)

#第三个卷积块的池化层,输入为F8和F9融合后的

#特征,输出为池化操作后的特征图F10。

VGG19同样是由两种类型的卷积块A和B组成。其中,VGG19卷积块A的结构和改进方式同VGG16的卷积块A完全相同。VGG19网络中的卷积块B,同样采用部分跨链的连接方式将网络卷积块中第一层与第二层特征图F1、F2结合作为第三层的输入F3,并将第二、三层得到的特征图再次结合,将得到的结果作为下一层的输入F4,最后将第三、四层得到的特征图融合后作为池化层的输入F5,最后对剩余的卷积块B做同样的处理。其中,卷积块B中前三个卷积层的连接方式与VGG16相同,所以F1到F4公式的表达方式与上一个公式的表达方式相同。特征图F5的表达公式如下:

F5=H(x0)+H(x1)+H(F4)=

H(x0)+H(x1)+H(H(x1)+H(H(x0)+H(x1)))

(7)

式中:Fi(i=1,2,3,4,5)分别代表第i个卷积层所得到的特征图的输入或输出,H(*)代表该卷积层的非线性操作,包括卷积或归一化等。xi(i=0,1,2,3,4)代表第i个卷积层的输出(i=0时表示上一个卷积块的输出)。

1.3 基于改进CPD算法的配准

1.3.1CPD算法的介绍

CPD算法是将参考图像与待配准图像生成的两个点集之间的对齐匹配问题转化为一种求解概率密度估计问题,该算法的基本原理是通过对一个确定点GMM(高斯混合模型)的后验概率进行求解,使其最大化,从而完成匹配。

在点集匹配中,一般是由两个点集构成,其中一个是参考点集XN×D(x1,x2,…,xN)T是由参考图像Ix生成的;另外的一个点集是高斯混合模型的中心点集YM×D(y1,y2,…,yM)T,需要将其向参考点集逐渐逼近。其中,N、M、D分别是参考图像和待配准图像生成相对应点集所包含特征点的数量和点集的维数。同时我们将一个均匀分布引入到了高斯混合模型中,是为了消除噪声等其他相关因素的影响。因此本文最后模型的高斯混合分量总和包含有协方差和混合概率,公式如下:

式中:ρ(x|m)一般是概率密度函数中所包含的基函数,ω(0≤ω≤1)是一个权重参数,m是根据待配准图像生成相应点集中的第m个特征点,x和y分别代表参考和待配准图像生成相应点集中的特征点。

高斯混合模型的质心位置可以通过对变换参数θ进行一系列调整从而实现变换,实际上是通过对下面公式中的负对数似然函数进行求解实现最小化,从而完成对这些参数进行估计,公式如下:

式中:θ为待估参数,实际意义为GMM质心位置的变换参数,σ2表示协方差,n是根据参考图像生成相应点集中第n个特征点。用期望值最大化(EM)算法来得到θ和σ2。

可以看出,权重参数ω在该算法中同样十分重要,一般来说它的数值是由人工进行随机给定的,但是如果给定的数值设计不合理,最终将会影响配准结果。本文为了得到合理的ω值,从而提高图像配准的精度,引入了粒子群算法(PSO)优化算法对ω进行自动寻找最优解。

1.3.2PSO优化的策略

为了解决上述ω值设定不合理的问题,本文首先设计一个准则函数用来对得到的ω值进行判定看是否合理,如果数值并不是十分合理,然后利用粒子群优化算法针对给定的ω值自动寻优。

粒子群算法[10-12]同随机优化算法中的遗传算法类似,算法主要步骤如下:首先给定一组随机解,然后通过迭代运算得到最优解,最后通过准则函数对最终得到的结果进行评价分析。其优势与遗传算法相比体现在,没有遗传算法的“交叉”和“变异”操作,比较简单,精度较高,收敛快,并且有较强的局部搜索能力。

为了权重参数ω能够实现自动迭代寻优,准则函数的选取必须是与ω相关的。这里选用距离误差作为度量标准,即把两个点集中对应点的欧氏距离作为准则函数。在实际情况中,点集的匹配过程中可能存在多对一的情况,如果准则函数还对每一个相关的点对做相同的处理,则会造成最后的配准误差较大,针对这一问题,本文提出按照距离的远近进行反比例的分配权重。换句话说,距离远权重小,反之权重大,准则函数公式如下:

式中:N为参考图像生成点集的特征点数量,i是第几个特征点,W是权重函数,x是两个点集中其中一个点集中特征点,Tx是另一个点集中与之相对应的特征点,d是两个点集中相关对应点对之间的欧氏距离。

式中:Dmax是对应点欧氏距离的最大值。

使用权重参数优化后的CPD算法进行特征点精确匹配,并根据最终的正确匹配特征点求出最终的仿射变换系数,待配准图像根据该系数进行仿射变换,从而完成对遥感图像的精确配准。

2 图像配准过程

本文提出的遥感图像配准算法的具体步骤如下:

(1) 特征提取。对输入的图像对利用训练好的双通道卷积神经网络模型进行特征提取。

(2) 特征融合。将来自两个不同通道提取的图像特征进行融合,利用融合后的特征生成相应的特征点集。

(3) 特征匹配。利用一致性点漂移算法对参考图像和待配准图像的特征点进行匹配,用来求解最佳转换参数。

(4) 求解变换模型。计算图像变换矩阵,待配准图像根据该仿射系数进行变换,完成遥感图像配准。具体流程如图5所示。

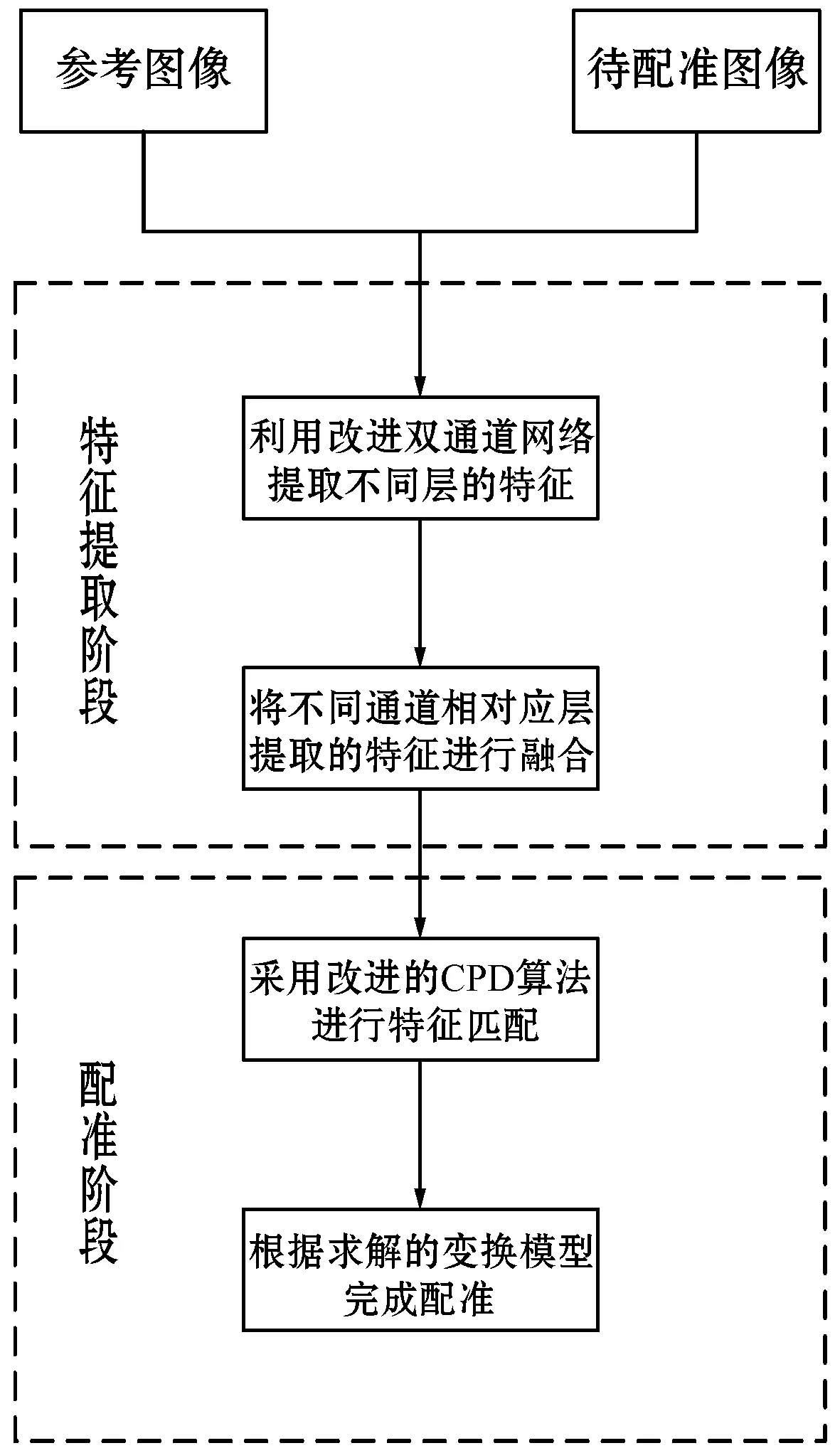
图5 本文方法配准流程

3 实验与结果分析

本文实验编译环境、实验测试环境和实验训练设备条件如表1所示。

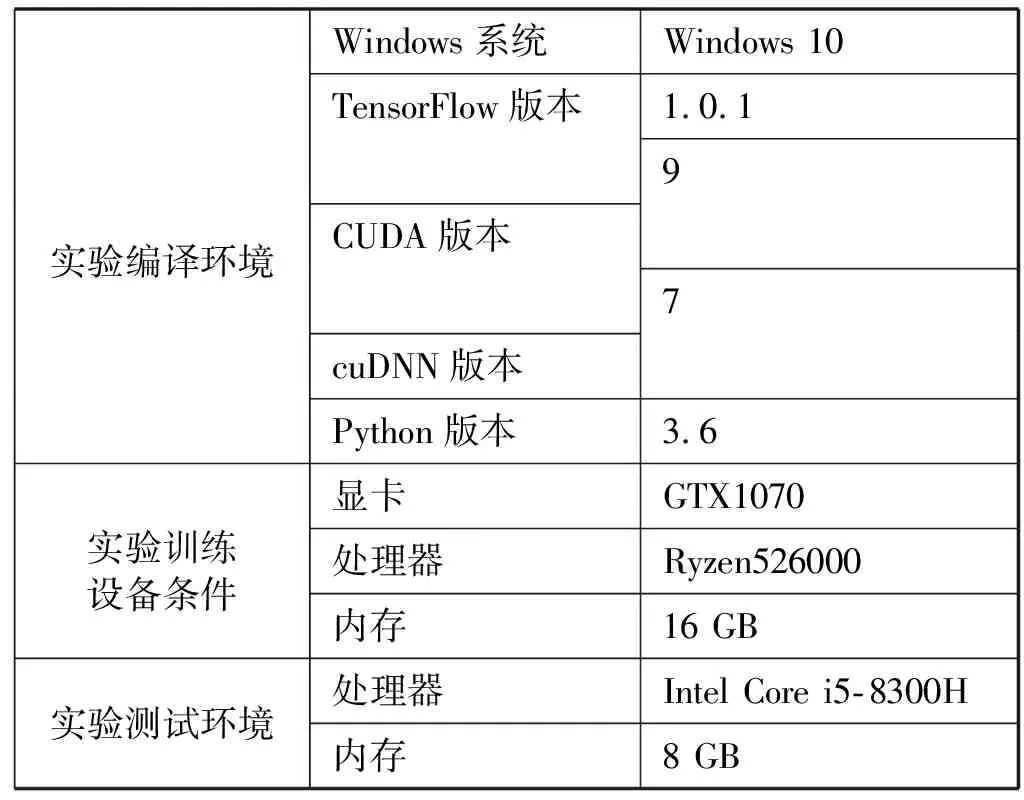
表1 各种实验操作的环境和设备条件

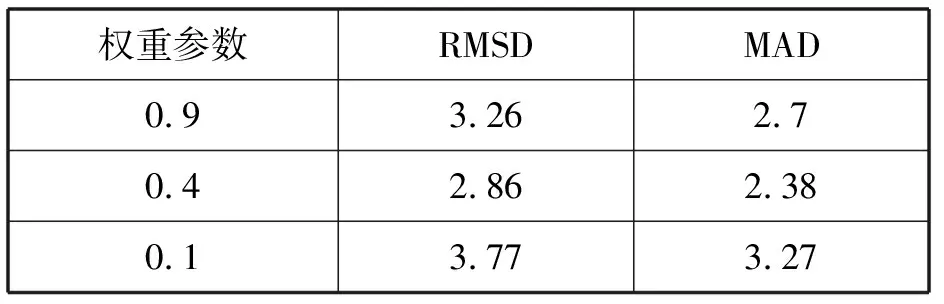
表2 各种权值参数下的误差值

3.1 数据集和参数设置

首先将预先训练好的VGG模型在ImageNet数据集上完成对参数进行初始化,然后使用自制的遥感图像数据集对搭建好的双通道模型进行训练,从而得到具有更好配准属性的多层融合特征。本文数据集构建使用AID数据集中59组多时相遥感图像对。根据图像类别可分为如下几类:野外遥感图像、城市遥感图像和景观图像。占比最大的是第一类,其余两类占比小且数量大致相同。其中野外遥感图像以界限分明的湖泊、河流遥感图像为主。在59对图像上分别选择Z个匹配“种子”图像块,其大小为32×32像素。这些“种子”图像块对中的每一个都被声明为代表它自己的类。为了扩展这些类,将K=210个随机变换应用于每个“种子”图像块对。每个变换是多个随机基本变换的组合,主要包括旋转、平移、缩放和亮度等。因此,本文构建的自定义数据集共有Z类,每个类包含2K个样本,并将生成的数据集按照4∶1的比例随机分成为训练集和测试数据集。

本文用均方根误差(Root Mean Square Distance,RMSD)、平均绝对误差(Mean Absolute Distance,MAD)、均方误差(Mean Square Error,MSE)等参数数据对图像配准精度做客观的评价。所有数据结果均是越小越好,单位是像素。

本文中的实验参数设置如下:根据经验得出学习速率一般设置为0.000 9,系统默认动量值和权重衰减值分别为0.9和0.000 5,一般不作修改。双通道网络多层特征融合模型在本文构建的数据集上的训练精度和测试精度如图6所示。

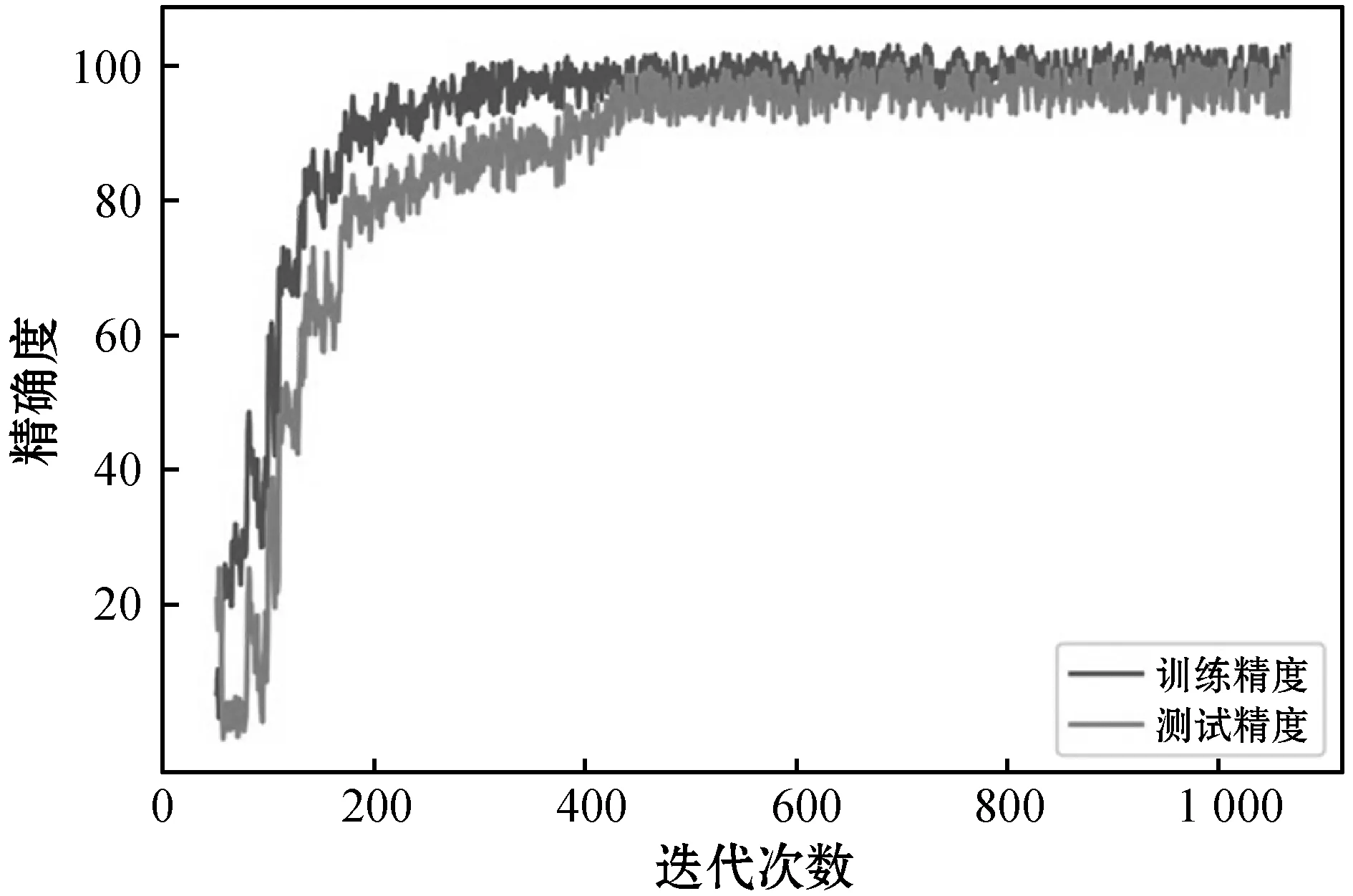
图6 数据集训练精度和测试精度

根据对权重参数ω自动寻优,得出当ω=0.4时效果最好。选取由数据来源GoogleEarth制作成的AID遥感数据集中分辨率均为600×600的湖泊、森林、山峦三种类型的测试图像对本文的算法的可行性进行验证,并且选取初始、最佳和最小权重参数进行实验对比,结果如图7所示。

(a) 参考图像

ω=0.9

可以看出,当权重参数ω=0.4时,对应的各个误差值均取得最小;比初始权重ω=0.9时,RMSD和MAD的误差损失率分别下降了12.1%和12%;比最小权重ω=0.1时,RMSD和MAD的误差损失率分别下降了24.1%和27.4%。因此权重参数ω=0.4时,配准效果最好。

3.2 本文实验结果

为了客观比较分析,本文通过对比其他三种传统配准算法和一种深度学习图像配准方法,并在三组不同地貌差异性的实验测试图像对条件下进行对比分析。

图8展示了三组测试图像利用本文方法与SIFT算法、文献[13]、文献[14]及文献[15]四种方法的对比试验,总共三组图像对的配准结果,其中第一组的图像对的差异性较小,第二和三组的图像对在外观上存在显著差异。

(a) 参考图像

3.3 实验结果分析

第一组来自GoogleEarth的图像的分辨率大小为600×600且图像的差异性较小、图像无亮度和视觉方面的变换,SIFT算法、文献[13]和文献[14]采用的是传统的配准算法,而文献[15]和本文采用的是通过深度学习完成对图像特征的提取,根据得到的特征生成相应的特征点之后完成图像配准。对于上述的4种算法都可以比较不错的配准结果。对于后两组的图像对分别来自高分2号制作的DOTA数据集中分辨率大小为953×1 094和高分3号制作的SAR-Ship数据集中分辨率大小为256×256的图像且在外观上存在较大差异。SIFT算法、文献[13]和文献[14]等传统算法在提取特征时可能有较多外点或特征点不足,所以配准效果明显劣于深度学习算法。文献[15]仅采用的是VGG单通道网络对图像进行配准,本文方法通过密集网络增加图像的特征重复利用率,同时使用双通道网络结构丰富了提取的图像特征。通过比较可以看出采用本文的方法所得到的配准效果在局部地区比其他方法的配准效果较好。

本文在所测试图像上均匀,随机地选择10组点用作配准误差测试,通过计算得出各组的实验数据如表3所示。

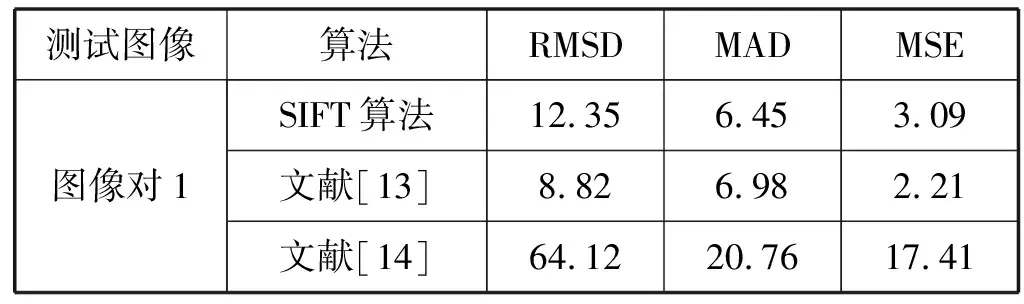
表3 与其他方法定量对比

五种方法的RMSD、MAD、MSE的平均值结果如图9所示。

图9 图像定量分析平均值

通过对上面五组的数据对比得出,本文对比实验数据RMSD、MAD、MSE三者的均值分别比各种对比实验中最好的数值平均降低了49%、25%、55%,可以看出传统算法和采用单通道的卷积神经网络的配准效果同样也不如本文的方法。因此,本文的算法具有更好的普适性,采用本文的方法对于具有显著地貌差异的遥感图像配准,可以得到较好的配准结果。

4 应用前景

随着科技的进步,遥感对地观测技术不断提高,其已广泛应用于测绘、水文、气象、国防、能源、交通等领域。遥感图像配准导航以其分辨率高、被动工作方式以及机载设备体积小、重量轻等显著优点在飞行器精确导航领域受到越来越多的重视,成为未来自主导航飞行器的主要方式之一。遥感图像配准技术是飞行器导航系统的核心,决定了导航系统的总体性能。遥感图像配准算法的适应性、可靠性、实时性以及定位精度是衡量遥感图像配准算法的主要技术指标。遥感图像匹配辅助导航系统中,参考图是在地面事先制备的卫星遥感图像或航拍图像,而实时图像是飞行器在运动过程中实时获取的地物景象,由于成像的天气、时间等自然条件、成像传感器性能和成像传感器的姿态差异、地面纹理特征等方面的不同,使得参考图与实时图像之间存在着较大的差异。面对飞行器如此复杂的工作环境,研究鲁棒性好、实时性高的遥感图像配准算法,满足飞行器导航的实际需要,是遥感图像配准技术研究的核心问题。

对于一艘航行中的船舶而言,最为基础也最为重要的就是船舶周边的视景获取,它能增强船舶对环境的感知能力,对于预判航行轨迹、海事分析、规避碰撞、地貌科学研究以及航海人员的培训等具有重大意义。船舶图像系统属于船舶安全驾驶辅助系统的一种,主要利用图像处理技术,经过畸变还原、视角转化、图像配准、图像增强等流程实时获取船舶周边景象,生成全景图或视野盲区景象图,再结合目标识别、检测和定位等计算机视觉领域的先进技术,形成一套可以辅助航海人员安全驾驶、加强船舶信息化建设的系统。其中,全景图像配准在船舶图像系统中有着举足轻重的地位,它是指将多幅具有部分重叠区域的窄视角图像进行无缝拼接,生成超宽视场的高分辨率图像的技术,该技术能够弥补常规相机的不足,解决人眼视角窄、盲区等问题。

5 结 语

本文提出的遥感图像配准改进算法主要体现在图像的特征提取及匹配。算法利用密集结构改进的双通道卷积神经网络进行特征提取,丰富了图像提取特征的同时提高了特征的重复利用率。同时采用随机优化算法改进的一致性点漂移算法进行特征匹配,提高了特征匹配的精度。实验表明,所提方法的配准结果具有比其他方法更好的效果。此外,本文方法对发生较大变化的遥感图像的配准具有更好的鲁棒性。