基于几何感知双流网络的无监督域自适应模型
韩彦净 马米米 张淑莉
1(郑州工商学院工学院 河南 郑州 450000)2(河南工业大学 河南 郑州 450000)
0 引 言
随着深度学习研究和应用,大数据领域中的数据挖掘算法也得到了飞速发展,其中训练数据集和测试数据集之间的认知偏差是数据挖掘的一个关键问题[1]。因此,如何实现源域与目标域之间的域自适应成为了研究的热点之一。
近年来,学者们研究提出了许多无监督领域自适应方法。它们可以归纳为三类:实例选择、模型精化和表示自适应[2]。实例选择是解决目标域中缺少标签问题的一种传统方法,文献[3]以高置信度选择目标实例指导无监督域自适应,迭代降低目标域标签预测的不确定性。文献[4]针对由于类不平衡导致模型泛化性能差的问题,提出了一种基于平衡概率分布和实例的迁移学习算法。实例选择方法虽然准确率较好,但其计算代价高,应用条件较为苛刻。模型精化是通过假设目标模型是源模型的移位,从而在无监督域自适应中使用一些标记的数据精化源模型来获得目标模型。文献[5]通过对目标数据的软标签分配,源域深度学习网络的迭代细化,从而实现了无监督域自适应。虽然上述方法取得了一定效果,但模型精化方法的灵活性较差,因为在域更新期间,模型体系结构在源域和目标域中都是固定的。另外,这些方法假设源域和目标域共享相似的底层流形,但上述假设在实践中难以保证。
表示自适应通过对齐跨域的数据分布来学习域不变特征,这样由对齐的源特征训练的模型可以应用于对齐的特征空间中的目标域。文献[6]将跨域分布对齐建模为流形中子空间的移动,子空间也被建模为主成分分析的特征向量或字典学习模型,源域和目标域分布通过在源和目标域之间插入子空间来对齐。文献[7]通过使用对抗性学习技术实现分布对齐,提出了对抗性适应网络来学习域之间的不可区分特征。文献[8]没有在每个域中保留几何结构,而是应用最大平均偏差(Maximum Mean Discrepancy,MMD)标准来匹配源域和目标域中的几何结构。然而当各域之间的几何图形不一致时源数据和目标数据依赖于不同的流形,源域和目标域几何体是不变的,这样就会导致源数据和目标数据无法对齐。即几何体保留会导致较差的自适应性能。另外,反映数据关系的几何信息不够具有代表性和可区分性,尤其是在没有标签的目标域中,因此,这种跨域几何体的直接对齐仅限于域自适应。
为了解决上述问题,提出一种基于几何感知双流网络的无监督域自适应模型。提出的几何感知双流网络用于学习相似表示和统一几何结构分布的源域目标域特征。在该网络中,统一准则被设计为源域和目标域几何的差异损失。最后实验结果验证了本文模型的有效性。
1 本文方法
1.1 问题描述
将源样本和目标样本分别表示为Xs∈Rp×ns和Xt∈Rp×nt。p表示每个源/目标样本的维度,ns和nt分别表示源和目标样本的总数。待学习的源特征和目标特征分别表示为Zs∈Rq×ns和Zt∈Rp×nt。通常,特征维数q远低于原始源/目标样本的维数,即q< 式中:Lf和Lg分别是特征对齐和几何对齐的损失函数;Θ表示模型中要学习的一组参数;γ表示平衡参数。 在式(1)中,在许多无监督域自适应方法中研究了用于特征对齐的损失函数Lf。因此,本文着重于几何对齐建模,并使用先进的对抗式学习技术来实现特征对齐。 1.2.1特征空间中的几何建模 式中:Nc(·)是一种列规范化操作,用于规范化每个源特征。 1.2.2数据几何的流形学习 式中:Dd是流形核的对角矩阵;Nc(·)表示列规范化。 在获得源域和目标域中的几何体后,本文目标是对齐εfs和εft以进行域自适应。但是目标标签不可用,因此源几何体和目标几何体之间的对应关系是未知的。假设几何体在域之间是一致的,即εs~εt,跨域对齐几何体的一种方法是几何体匹配,它学习对应关系,同时保留每个域中的几何体信息。优化过程表达式为: 式中:F是一个0-1矩阵,表示Xt和Xs之间的对应关系;Lps和Lpt分别是源域和目标域中的几何不变项。 然而,这种一致几何形状的假设在实践中是无效的,因此,式(5)无法在实际场景中实现几何对齐。为了处理跨域几何不一致的问题,对每对源和目标数据之间的对应概率进行估计,并将目标几何与源域对齐。在数学上,通过以下方法优化目标特征的几何结构εft: (7) 式中:Qdc∈Rnd×K记录了属于每个类别的样本的概率;k、k1和k2为类别索引;K为类别总数。 在式(7)中,Qdc指的是式(6)中的对应概率矩阵Q更容易估计的标签概率,但式(7)可能不收敛,因为它最小化了负平方项。为了避免不收敛,将式(7)改写为: (8) 将源特征Zs聚类为K组,同一组中的源要素具有相同的标签,并且分布紧密。相反,来自不同组的源要素具有不同的标签,并且来自不同组的源要素之间的几何距离统一为。 与源域不同,标签在目标域中不可用,因此无法直接获取Qtc。在本文中,通过限制目标特征位于一组源特征的邻域来近似学习目标域中的自适应几何。换言之,每个目标特征对于一个类别具有高概率。结合式(9)的约束,每个目标特征分布在靠近某个类别k的源样本的位置,而远离其他类别的样本的位置,固定距离为。这意味着εft中的值最小化或优化为。对于每个目标特征最小化两个不同类别的高概率即其中k1≠k2。求所有样品和类别的和通过最小化Lgt=Q′tcQtc-tr(Q′tcQtc)学习目标域自适应几何。 但如果没有目标标签的约束,每个目标样本的特征将任意接近随机类的源特征。为了避免任意对齐并使自适应几何学习更加可靠,本文为目标域几何集成了一致性损失。然后,目标域几何体的优化更新为: 式中:Lpt(εt,εft)是几何保持项,它约束目标特征和目标数据之间的几何一致性。 结合式(9)-式(10),研究了几何对齐的自适应几何学习优化问题: Q′tcQtc-tr(Q′tcQtc)+Lpt(εt,εft) (11) 为了实现式(1)中的总体目标函数,本文搭建了一个几何感知的双流网络,优化了Lf和Lg。几何感知双流网络由源CNN、目标CNN、域鉴别器和分类器组成。在训练阶段,给定带标签的源图像和未标记的目标图像,对网络进行特征和几何对齐的损失训练。在源域中,采用分类损失来进行特征识别。为了获得对齐特征,引入了对抗性学习算法,并使用域损失来区分目标特征和源样本特征。对于无监督几何对齐,设计了具有统一几何标准的几何一致性损失和差异损失,以满足式(11)中自适应几何学习的目标。训练后,利用训练后的源CNN提取源图像的特征。在测试阶段,使用训练的目标CNN将目标图像映射到对齐的特征空间。然后,通过训练的分类器对目标特征进行分类以预测类别标签,或者与源特征匹配以进行重新识别。整体结构如图1所示。 图1 整体结构 1.4.1源域中的分类丢失 本文将源CNN和目标CNN的映射分别表示为Ms和Mt,即Zs=Ms(Xs),Zt=Mt(Xt)。分类器表示为C,源域分类损失表示为: (12) 式中:ys表示源标签;k表示类的索引;C(Ms(Xs))∈Rns×K是概率矩阵;1[ys=k]是第k个元素中非零值的单位向量。 1.4.2非鉴别域损失 基于非鉴别域的思想,本文引入了域鉴别器D来对齐源和目标特征。如果D不能正确预测源和目标特征Z={Zs,Zt}的域标签,则将源特征Zs和目标特征Zt视为对齐。域不区分损失表示为交叉熵损失函数: LfM(Xs,Xt,Ms,Mt,D)=-EXt[logD(Mt(Xt))]- EXs[log(1-D(Ms(Xs)))] (13) 式中:源样本和目标样本的域标签分别为1和0。另外,将域鉴别器D设计为对抗网络,以确保其在分配期间的鉴别。域鉴别器D的损失函数为: LfD(Xs,Xt,Ms,Mt,D)=-EXs[logD(Ms(Xs))]- EXt[log(1-D(Mt(Xt)))] (14) 同时更新源CNN、目标CNN和域鉴别器的参数,忽略式(14)的情况下学习判别鉴别器。受式(13)的约束,即使是判别式鉴别器也无法正确预测源和目标特征的域标签。换言之,源特征Zs和目标特征Zt是对齐的。 1.4.3无监督几何对齐损失 式(11)优化以学习用于无监督几何对齐的自适应几何,优化分为两个损失:1) 达到域自适应几何统一标准的差异损失;2) 保留目标域几何信息的几何一致性损失。在源域中,本文将差异损失设为式(9)中的Lgs。为了计算目标域中的差异损失,引入式(12)中的分类器C来估计概率矩阵Qtc,即Qtc=C(Mt(Xt))∈Rnt×K。目标域差异损失公式如下: LgDt(Xt,Mt,C)=v′(C(Mt(Xt)))′C(Mt(Xt))v- tr((C(Mt(Xt)))′C(Mt(Xt))) (15) 式中:v∈RK×1是一个全为1的列向量;因此v′Av表示矩阵A中所有元素的总和。几何一致性损失是式(11)中的几何保留项Lpt,其计算公式为: 式中:H(ε,μ)=1/(1+e-(ε-μ))是一个具有Sigmoid函数中点μ的Logistic函数;μt和μft分别是εt和εft的平均值。利用式(16),相似的目标样本保持在特征空间中近的位置。因此,在对齐的目标特征之间保留目标域中的几何信息。 总之,几何感知双流网络需要解决以下优化问题: -EXs[log(1-D(Ms(Xs)))]- -EXt[log(D(Mt(Xt)))]+ γ(v′(C(Mt(Xt)))′C(Mt(Xt))v- tr((C(Mt(Xt)))′C(Mt(Xt)))) (18) EXt[log(1-D(Mt(Xt)))] (19) γ(v′(C(Mt(Xt)))′C(Mt(Xt))v- tr((C(Mt(Xt)))′C(Mt(Xt)))) (20) 将源CNN、目标CNN、域鉴别器和分类器的参数分别表示为θs、θt、θD和θC。为了解决上述优化问题,通过保持其他模块不变来优化θs、θt、θD和θC。在每次迭代中,计算参数的梯度,并使用小批量随机梯度下降(SGD)通过反向传播更新参数。 1.5.1θD和θC的梯度 式(19)和式(20)是可推导的,因为LfD和LC是典型的交叉熵损失,而LgDt是二次损失。通过简单地计算θD和θC的导数,得到了θD和θC的梯度∂LfD/∂θD和∂(LC+γLgDt)/∂θC,如下: 1.5.2θs的梯度 (24) 其中: (25) 总之,式(17)中θs的梯度是LfM、LC和Lgs梯度的总和: 1.5.3θt的梯度 类似地,采用无偏估计来降低式(18)中Lpt的复杂度,将Lpt的无偏估计表示为: (29) 式(18)的梯度是LfM、LgDt和Lpt梯度的组合: 算法1域自适应算法 输入:原始域Xs∈Rp×ns;目标域Xt∈Rp×nt,源标签ys,概率矩阵C(Ms(Xs))∈Rns×K,邻接矩阵εs∈Rns×ns和εt∈Rnt×nt,权衡系数γ。 输出:分类器C和域鉴别器D。 2.forido 3.forjdo 5.根据式(19)最小化LfD; 6.end for 7.end for 8.forido 9.forjdo 11.根据式(18)最小化LfM(Xt,Mt,D)+γLgDt(Xt,Mt,C)+γLpt(εft,εt); 12.end for 13.end for 14.forido 15.forjdo 17.根据式(17)最小化LfM(Xs,Ms,D)+LC(Xs,Ms,D)+γLgs(εfs); 18.end for 19.end for 20.forido 21.forjdo 23.根据式(20)最小化LC+γLgDt; 24.end for 25.end for 1) 跨数据集数字识别:MNIST、USPS和SVHN数据集包含十类数字的图像。简而言之,M、U和S字符分别用于表示MNIST、USPS和SVHN数据集[9]。根据文献[10]无监督域自适应模型中的设置,在四个自适应方向上对所提出的模型进行评估:M→U、M→S、U→M和S→M。 2) 跨数据集对象识别:本文方法也在Office Home数据集上进行了评估。该数据集由四个领域组成:Art(Ar)、Clipart(Cl)、Product(Pr)和Real-World(Rw)。每个域都有65种常见的图像。通过所有12项适应任务来评估本文方法。 3) 跨模态行人再识别:本文在RegDB数据集上验证了本文方法,该数据集包含由双摄像头系统捕获的412位人的图像。RegDB数据集中包含两个子数据集:(1) 可见数据集(V),每个人有10个可见光图像;(2) 热成像数据集(T),每个人有10个不同的热图像。按照文献[11]中的实验方案,将可见光图数据集和热成像数据集随机分成两份,用于训练和测试。通过重新识别训练和测试数据集中的人员来评估几何对齐特征。 4) 合成数据图像分类:Syn2Real是视觉领域适应的数据集。该数据集由从三维对象模型渲染的合成数据集和具有相同对象类别的真实图像数据集组成,从合成和真实数据集中选择12类对象进行实验,合成数据集和真实数据集分别是源域和目标域。 对于跨数据集数字识别实验,源CNN和目标CNN由LeNet实现。在跨数据集对象识别中,ResNet-50用于特征提取。在其他识别任务中,选择由五个卷积层和三个全连接层组成的AlexNet来实现源和目标CNN。按照文献[12]中搭建的神经网络,将域鉴别器D设计为具有3个全连接层、500个隐藏层和输出层的深度学习网络。用于标签预测的分类器C是一个全连接层,其输出是类标签的概率向量。在本实验中,平衡参数γ设为1。本文所有实验均在MATLAB2016上进行,计算机的配置为2.5 GHz处理器和8 GB内存。 将本文方法与各种无监督域自适应模型进行了比较,包括:深度自适应网络(DAN)[2]、加权最大平均差异(WMMD)[7]、区分域自适应(ADDA)[4]、联合几何和统计对齐(JGSA)[13]、分层对抗性深域自适应(HAND)[14]、最大分类器差异(MCD)[15]、条件对抗域自适应(CDAN)[9]、随机邻域嵌入(d-SNE)[10]和切片Wasserstein差异(SWD)[11]模型等。为了公平起见,实验过程中,这些方法采用相同的深度学习模型骨干网络,源CNN的结果也作为基准方法进行比较分析。 2.3.1跨数据集数字识别 跨数据集数字识别的实验结果如表1所示。实验结果表明,与其他模型相比,该模型在四位数字识别实验中表现良好。该模型的平均准确率为80.0%,是所有无监督域自适应模型中准确性最高的。 表1 跨数据集的数字识别性能(%) 2.3.2跨数据集对象识别 表2总结了跨Office Home数据集的对象识别结果。结果表明,该模型在目标域的识别性能提高了17.1百分点。对于大多数自适应任务,本文方法也优于其他无监督域自适应模型。得到的平均准确率为63.2%,高于表2中列出的其他无监督适应模型。 表2 Office Home数据集上跨数据集对象识别性能(%) 2.3.3跨模态行人再识别 如3.1节所述,可视和热数据集中的人员随机分成两半进行训练和测试。在训练阶段,将带有标签的模态的训练图像(源域)和另一个没有标签的模态的训练图像(目标域)作为网络中的输入。在测试阶段,目标域中的图像用作测试集,而源域中的图像用作库集,对目标域训练和测试数据集都进行了验证,进行了十次实验。在每次训练中,都会挑选不同的人员进行训练。表3总结了每个实验的平均准确率(mAP)结果。本文方法在目标域训练和测试数据集的所有实验中都取得了最好的结果,在目标域训练和测试数据集中,分别改善了16.0%和7.3%。 表3 RegDB数据集上跨模式人员重新识别的mAP(%) 表4中总结了Top20的匹配分数。结果表明,在目标域训练数据集中,AlexNet特征比人工特征(HOG和mLBP)获得了更好的性能。但是,目标域测试数据集中AlexNet的性能与人工制作的性能一样差。相比之下,该模型在目标域的训练数据集和测试数据集上都达到了最高的平均准确率,这表明所提出的几何对齐特征具有更好的泛化能力。此外,标准累积匹配特性(CMC)曲线如图2所示,以进一步说明几何对齐特征的性能。与每个实验中的其他模型相比,本文模型在几乎所有级别上都获得了最高的匹配分数。 表4 RegDB数据集上跨模态行人重识别的性能(%) (a) 源:可视,目标:热 (b) 源:可视,目标:热 (c) 源:热,目标:可视 2.3.4合成图像分类 在十次实验中也包含了合成图像的分类实验,并计算了平均结果。在每个实验中,从Syn2Real数据集中随机选择十分之一的合成图像和真实图像进行实验。图3说明了真实图像数据集中(目标域)每个类别的识别准确率。结果表明,本文方法不仅提高了平均准确率,而且提高了目标域中大多数图像类别(12个类别中的9个)的识别性能。 图3 算法在真实图像分类中的性能 2.4.1消融研究 无监督几何对齐通过三种损失获得:源域和目标域差异损失(Lgs和LgDt)和几何一致性损失(Lpt)。为了分析这些损失对性能的影响,消融实验通过在几何感知双流网络中部分应用这些损失来完成。表5总结了跨数据集对象识别的结果,以供分析。源域CNN作为基线模型,从这些表中,可以发现本文方法通过仅使用源域差异损失(Lgs)来提高性能。这是因为在Lgs约束下,特征对类标签更具区分性。通过应用参考自适应几何体统一标准的Lgs和LgDt,可以实现更大的准确率提高。本文方法的平均结果从56.2%进一步提高到59.5%。结合目标域几何一致性损失(Lpt),本文方法的性能得到进一步提高,平均准确率达到63.2%。 表5 交叉数据集识别中消融实验的性能(%) 2.4.2稳定性分析 本节分析十次实验的准确率方差,以证明本文方法的稳定性。交叉数据集数字识别的结果与表6中现有的无监督方法进行了比较。对于每对数据集,最高方差以加粗显示。结果表明,本文方法的方差不是最大的,这表明该模型的方差是可以接受的。此外,与同样由对抗网络组成的ADDA相比,本文方法获得了更低的方差。因此,本文方法的性能相对稳定。 表6 数据集之间数字识别的准确度误差(%) 2.4.3参数灵敏度 本文模型的总体目标函数如式(1)所示,包括一个超参数γ,用于平衡表示和几何对齐。本节分析了参数敏感性实验的结果,以说明本文模型中参数γ对性能的影响。参数敏感性实验在数字数据集(MNIST、USPS和SVHN数据集)上进行。取不同的γ值,并保持其他实验参数值不变。γ值是通过指数函数选择的,范围为10-3至103,随γ值变化的跨域识别准确率如图4所示。结果表明,在大多数成对数据集中,当γ值从10开始增加时,本文方法的性能逐渐从10-3提高至10-1,这验证了学习自适应几何在提高域自适应性能方面的有效性。当γ>1时,本文方法的准确性降低,这意味着不需要对几何对齐(Lg)赋予较大的权重。特别是如果γ太大(γ>102),几何对齐(Lg)会损害表示对齐(Lf)。可以在图4中发现,当γ设置为103时,跨数据集识别准确率显著下降。 图4 随γ值变化的跨域识别准确率比较 本文重点解决闭集域适配问题,其中源域和目标域的标签空间相同。为了说明域共享标签数量的影响,在标签移位设置下进一步评估了本文模型。实验在数字数据集上进行,借鉴开放集合域适配的实验设置,其中源域和目标域的标签空间部分重叠。非重叠标签在源域和目标域中用作“未知”类。测试了不同域标签的不同重叠率(20%、40%、60%和80%)。实验中选择数字0-1、0-3、0-5和0-7作为域共享标签,重叠率分别为20%、40%、60%和80%。源域和目标域都包含域共享标签的示例。除重叠标签外,其余标签的一半样本包含在源域中,而另一半标签的样本包含在目标域中,具有不同标签重叠率(LOR)的开放集域适配结果如表7所示。表7中报告了域共享类的准确率、目标域“未知”类的结果、目标域中所有类的平均结果,还总结了源模型(表示为CNN)的结果以供比较。 表7 数字数据集的开放集域自适应结果(%) 表7中的结果表明,一般而言,随着域共享标签数量的增加(LOR的增加),源模型(CNN)在识别域共享类方面的性能降低。这是因为在大型LOR的情况下,需要识别更多的域共享类,这增加了目标域中数字识别的难度。目标域“未知”类别上的源模型性能(CNN)也随着LOR的增加而降低。原因可能是,随着域共享标签数量的增加,“未知”类的目标样本可能更容易错误分类到某个域共享类中。 可以发现,与源模型(CNN)的结果相比,当LOR大于20%时,本文模型在大多数开放集域自适应实验中提高了跨域识别性能。但在LOR为20%的某些情况下,本文方法对于域共享类的准确率较低,例如,当M→S,仅为2.9%。这是因为当LOR较小时,目标域包含许多带有新标签的样本。因此,域共享类的样本很可能通过跨域的几何对齐被误分类为“未知”类的样本。虽然本文方法的性能不如在闭集域自适应实验中稳定,但在某些情况下,本文方法表现较好。例如,当LOR为80%、U→M时,本文方法将平均准确度提高了34.1百分点。这一结果表明了学习自适应几何在开放集域自适应中的有效性。 本节通过可视化几何对齐的特征并在特征空间中列出目标样本的最近邻域源来考察本文方法的性能。 2.6.1特征可视化 使用图5中的t-SNE可视化本文方法的源和目标特征。选择数据集U→M和M→U作为图示。原始像素值的数据分布作为基线,图5中还说明了从LeNet[16]和ADDA中提取的特征进行比较。符号∘和+分别用于标记源域和目标域中的数据/要素。 (a) U→M原始特征 在图5(a)、图5(e)中,独立分布源数据集和目标数据集的样本,可见源数据域和目标数据域之间存在较大的域偏移。图5(b)、图5(f)为LeNet特征的分布。结果表明,LeNet特征对于类别标签更容易区分,因为这些特征是从源图像及其标签中学习的。但源特征和目标特征仍然没有很好地匹配,这意味着深度学习特征中仍然存在数据集偏差问题。因此,一些目标样本会被源模型使用深度学习特征错误分类。 与LeNet特征相比,来自源数据集和目标数据集的ADDA特征的边缘分布的一致性更强,如图5(c)-图5(g)所示。这反映了对抗性适应的特征对齐效果。然而,可以发现每个目标样本都是任意对齐到一个源样本簇。因此,源数据集和目标数据集的几何形状(邻域关系)是不同的。另外,来自不同类别的一些目标样本在ADDA特征空间中紧密分布,导致这些类别的样本分类困难。 相比之下,本文模型在源域和目标域之间对齐表示和几何体,如图5(d)、图5(h)所示,源与目标的几何对齐特征具有相似的分布。此外,在统一几何准则的约束下,同一类的样本以小方差聚类,分别单独分布不同类的样本。结果表明,由于目标样本的映射受到几何一致性约束的指导,目标样本映射到错误类的可能性较小。因此,目标数据集的几何对齐特征对类标签的区别更大。 2.6.2最近邻域源的可视化 本文将一些目标样本及其五个最近邻域源进行可视化,从而说明了特征空间中的邻域关系。如图5所示,选取跨模态行人再识别(V→T,T→V)的结果进行说明。可以看出,目标样本与其邻域中的源图像具有相似的特征。 (a) T→V 为了克服几何信息不具有代表性和可区分性等缺点,提出一种基于几何感知双流网络的无监督域自适应模型。最后分析实验结果可以得出如下结论: (1) 提出的域自适应模型能够在跨数据集对象识别、跨模态行人再识别、开放集合域自适应中均表现出较好的识别准确率,证明了几何对齐有效提高了识别模型在目标域的泛化能力。 (2) 提出的模型获得了更低的方差,因此验证了该模型具有相对稳定的识别性能。另外由于目标样本的映射受到几何一致性约束的指导,目标样本映射到错误类的可能性较小。因此,目标数据集的几何对齐特征对类标签的区别更大。 (3) 随着域共享标签数量的增加,源模型在识别域共享类方面的性能降低。目标域“未知”类别上的源模型性能也随着域共享标签数量的增加而降低。1.2 几何理论



1.3 用于无监督几何对齐的自适应几何学习




1.4 几何感知双流网络

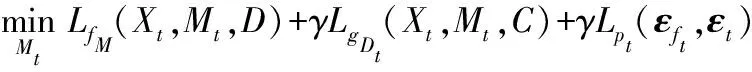
1.5 优化过程
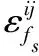

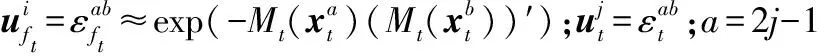


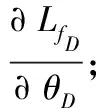
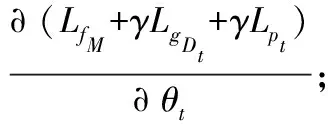

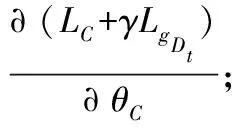
2 实验与结果分析
2.1 数据集
2.2 实验设置
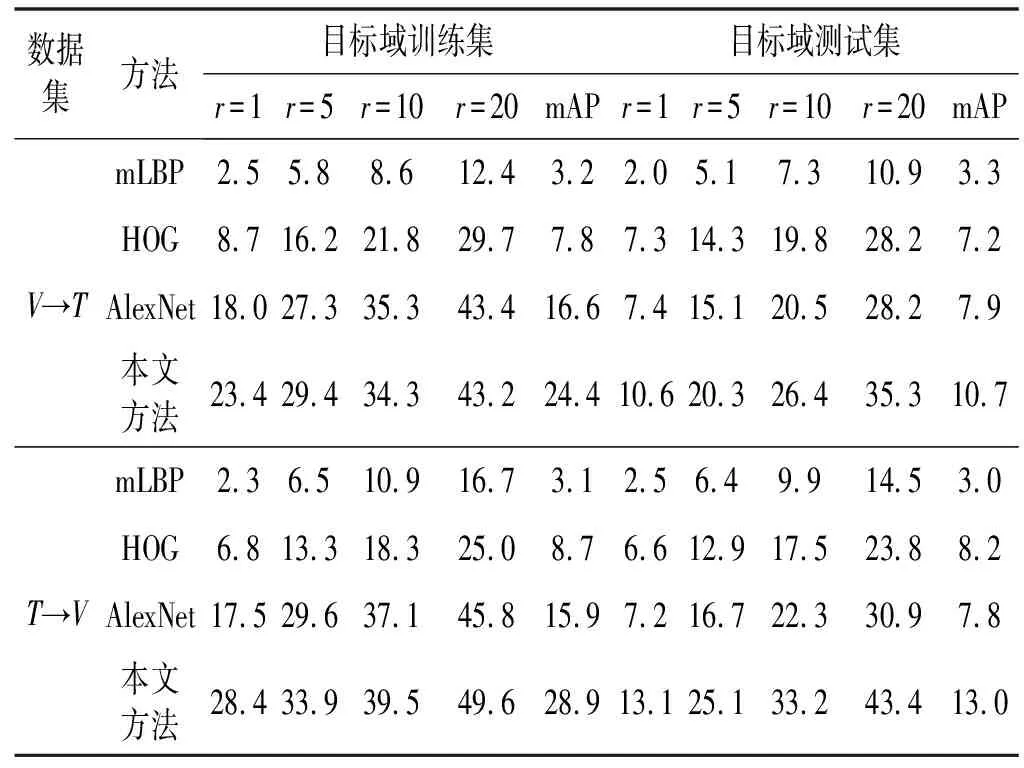
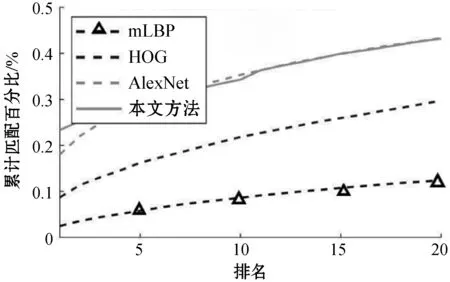
2.3 实验结果






2.4 性能分析



2.5 开放集合域自适应

2.6 可视化


3 结 语

