三维折射修正模型在土样变形测量中的应用

叶锴 夏燚 牟春梅

摘要：

三轴试验的摄影测量中，压力室和不同介质产生的折射放大效应对测量结果影响很大。为探寻工程特性完全不同的土对折射效应的敏感程度，基于光线追踪技术建立了三维折射修正模型，选取具有代表性的桂林红黏土与一般砂土作为试验材料进行研究。试验中以摄影测量法直接得到土样变形值作为折射修正前值，以消除折射影响的土样变形值作为折射修正后值，选择轴向变形值和径向变形值作为考虑折射效应的影响指标。试验结果表明：① 折射效应的影响对两种土样的轴向变形可以忽略不计，但对径向变形起到了放大作用，红黏土在径向上放大1.25倍，砂土在径向上放大1.32倍；② 摄影测量法应用于三轴试验变形测量时，不能通过一个固定的修正系数实现对所有不同土样的折射修正，而是要针对不同土样的工程特性给出不同的折射修正系数。

关 键 词：

三轴试验； 折射放大效应； 光线追踪； 三维折射修正模型； 摄影测量法

中图法分类号： TU411

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.07.025

0 引 言

三轴试验作为测量土体应力、强度、弹性模量等物理力学性质的有效方法，其通过三轴体变管排水量的换算得出饱和土的体积变化［1］。受试验仪器和土样变形计算方法的限制，上述测量方式仍存在一些不足［2-5］：① 透水石、基座、试样帽、轴向位移传感器与三轴土样之间存在间隙，测量的轴向变形包含了端部空隙和土样变形；② 常规测量方法得到的径向变形是假定相等的，并不能够反映土样的实际径向变形；③ 传统三轴试验测量结果通常只能得到土样在试验过程中的总体积变化量，无法反映土样各部分的体积变化；④ 传统三轴试验仅能得到饱和试样的平均体积变化，对非饱和土的测量存在困难。

目前土样变形测量的方法主要分为接触式测量和非接触式测量。如陈超斌等［6］利用安装有 LVDT［7］（Linear Variable Differential Transformer）位移传感器的三轴仪对上海软土土样的局部变形进行测量（属于接触式），取得了良好的测量结果且有较高的精度保障，但对于试验环境敏感且对土样会产生一定的约束作用［8］。随着非接触式测量的发展，一种根据二维图像获得目标物体的三维空间坐标，借助计算机视觉技术重构出物体的三维空间模型，完成被摄物体几何、位移变形测量的技术正迅速发展［9-10］，具有非接触、无干扰、适用性广等优点。

在非接触式测量中，为消除折射效应的影响，Bhandari［11］、Zhang［12］等通过折射定律计算光线偏移角度，根据相机与压力室距离、土样初始半径、压力室内外半径等参数建立二维平面校正模型，用以消除折射效应对图像测量结果的影响；Bhandari等［13］通过线性函数修正法抵消折射产生的变形。Rechenmacher等［14］在图像测量过程中，采用真空加压的方法来消除常规三轴仪上由于折射引起的图像变形问题；邵龙潭团队［15-16］研发的三轴土样全表面变形数字图像测量系统，通过改造压力室将弧形观测面更换为平面观测面以减小折射效应的影响。上述修正仍有不少缺陷，如线性函数的使用条件需要土样变形过程中折射效应的影响不变，且外界因素的不确定性也使修正系数法并不能完全适用于土样全变形过程；使用真空加压或改制压力室罩虽然能够有效消除折射，但并不适合多数三轴试验。

为探究工程特性完全不同的土对折射效应的敏感程度，本文使用单镜头相机进行图像采集，并在常规三轴仪的压力室表面和荷载架上粘贴编码点来获取压力室变形参数，构建压力室变形数学模型，以此确定折射面。再结合光线追踪原理建立三维折射修正模型消除压力室壁和不同介质造成的折射影响。通过对比红黏土不固结不排水试验和砂土固结排水试验中经过折射修正前后的轴向和径向土样变形，得出三维折射修正模型对不同土样变形测量结果的影响。

2 三轴数字化测量

2.1 编码点设置

数字化测量需在压力室表面、荷载架上和特制的橡皮膜上粘贴编码点。首先在包裹土樣的橡皮膜表面上以10 mm的间隔粘贴8行×16列共128个编码点（0.9 mm）；在压力室表面粘贴180个编码点，上下各两圈和3个垂直列，用于构造压力室表面参数模型，如图7所示。

2.2 图像采集方式

编码点设置完成后，安装三轴土样。在确保外部光源充足的情况下，使用相机以不同距离、不同方位对土样进行环绕拍摄，总计拍摄45～50张图片。为确保图片具有足够的重叠率，使重构出来的土样模型数据满足试验要求，需保证连续3张不同方位的拍摄图片至少出现同一编码点。具体的图像采集方式如图8所示。

2.3 建立修正模型

以三轴仪两侧粘贴的编码点作为数据源建立世界坐标系（O-XYZ）。用游标卡尺（0.02 mm）测量两加载杆的距离，输入PM软件获得世界坐标系的比例尺。通过1.4节建立的压力室变形数学模型确定折射面。依据式（7）算得入射角和折射率。借助Snell定律，确定入射光线在不同介质面的交点及折射方向［19］。如图9所示，建立三维折射修正模型，至少需要3条折射光线作为数据源：

n1sinI1=n2sinI2n2sinI2=n3sinI3（7）

式中：n1、n2为折射率，I1、I2为其入射角。

2.4 图像数据处理

将图片导入PhotoModeler Scanner软件中进行识别处理。每次图像采集与前一次图像采集保证85%以上的图像重叠率。运行软件提取每次拍摄的相机方位、编码点在图片中的像素坐标、压力室表面的三维世界坐标。但由于压力室壁和密闭介质的折射放大效应，提取的数据须经过三维折射修正模型进行修正，使用Matlab编写相应的计算程序进行计算，得到试样实际三维空间坐标。

3 测量精度分析

三轴试验的摄影测量中，光线穿越不同介质（空气→压力室罩→水）而产生的折射放大效应，会使压力室中的土样在成像过程中也同步被放大。本文使用质地均匀的硬圆柱体作为三轴试样模型，并在其表面粘贴RAD编码点进行标识便于结果分析，具体如图10所示。在空气中，分別使用游标卡尺和摄影测量对三轴模型的竖向高度进行10次测量，其结果详见表2。

由表2可以得出，摄影测量法在空气中平均绝对误差为-0.038 mm，平均相对误差为-0.063%，误差值非常小，测量精度满足要求。

4 三维折射修正试验

4.1 土样参数

不固结不排水试验（试验1）采用的土样是广西桂林市某工地的红黏土，取土深度约1～2 m，颜色呈红褐色，硬塑状态。通过室内土工试验得到其部分基本物理力学指标如表3所列。依据GB/T 50123-2019《土工试验方法标准》规程，制备含水率为23%，干密度为1.6 g/cm3的三轴试样（直径39.1 mm，高度80 mm）。

三轴试验（试验2）采用的是石英砂土，粒径在0.3～0.6 mm范围内，依据GB/T 50123-2019《土工试验方法标准》对石英砂土进行物理性质试验，得到其部分基本物理力学指标如表4所列。基于此，采用干密度为1.6 g/cm3配比进行砂土的三轴土样制作（直径39.1 mm，高度为80 mm）。

4.2 试验方案

通过控制加载杆的轴向位移来进行试验，即在施加轴向力前先对土样进行拍摄，达到不同的位移值时暂停加载并再次拍摄图像，当土样轴向位移达到12 mm时，整体轴向应变达15%，认为试样破坏。

为了方便对比将两种试验土样按照10 mm分为1～8段截面，并将土样划分为上部（6～8）、中部（3～6）、下部（1～3），如图11所示。

5 试验结果

运用摄影测量法对空气中的三轴土样进行测量，得到土样各截面编码点坐标，导入Matlab软件进行光线追踪的折射修正并拟合成圆，从而确定土样不同截面的半径。求得不同土样在不同围压下经三维折射模型修正后及未经修正的轴向及径向测量值。

5.1 轴向变形分析

由表5可知，两种土样在不同围压下的轴向高度基本都在78 mm以上，土样均能被编码点包裹。经折射修正模型校正后的轴向测量值与空气中测量值极为接近，不同围压下的红黏土和砂土轴向测量值平均误差分别为0.118，0.131 mm，最大误差分别为0.140，0.155 mm。红黏土的轴向测量平均放大倍数为1.010 4倍，砂土为1.001 0倍。其原因是：三轴压力室壁的轴向截面近似平面，并且由于水、有机玻璃压力室、空气的折射率相近，多种介质的折射对成像光线向量的竖直分量曲折效果很小。可以判断不同土样在不同围压下折射效应对于土样轴向位移的测量结果影响很小。

5.2 径向变形分析

由表6可知，两种土样经折射模型修正后的测量值在径向上和空气中测量的真值极为吻合。不同围压下红黏土和砂土各土段的径向测量值平均误差分别为0.117 mm和0.139 mm，最大误差分别为0.211 mm和0.243 mm。红黏土样平均放大倍数为1.226倍，砂土为1.33倍。由此发现两种土样在径向界面所受折射影响远大于轴向上所受的影响，故需对试验进一步分析。

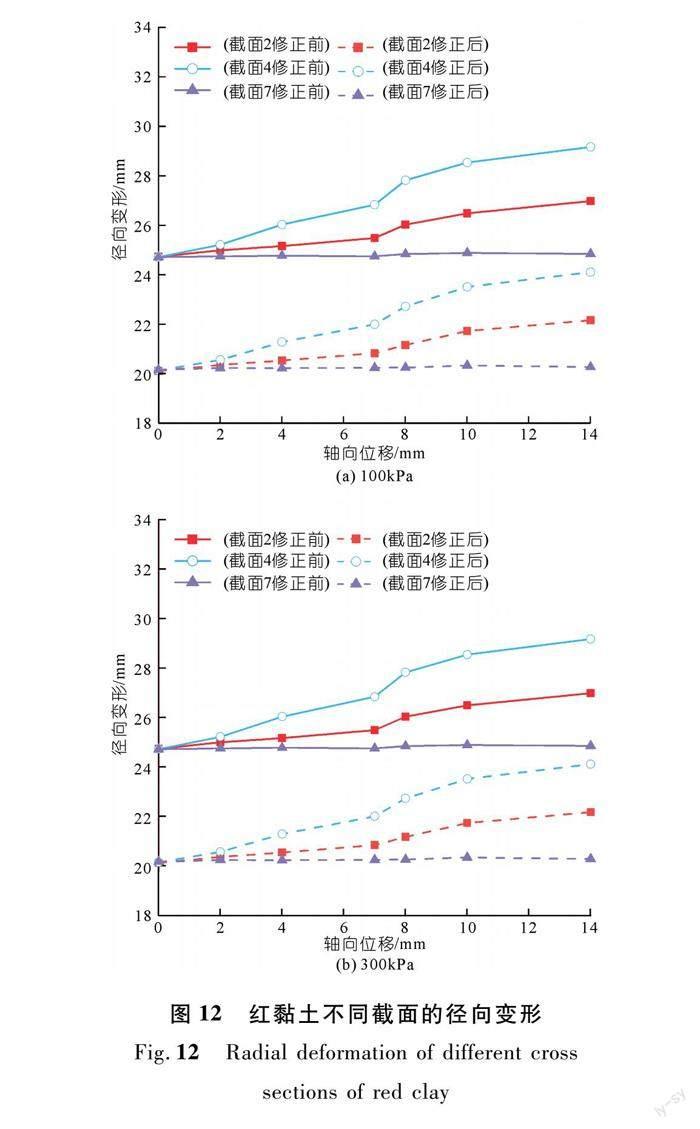
鉴于土样的不均匀性，按预先的土段划分选取截面7、截面4、截面2进行分析，如图12、13所示，以此突出土样的不均匀变形［20］。

由图12可知，100 kPa围压下截面2在试验1开始时修正前值是修正后值的1.28倍；试验结束时，实际数值被放大1.27倍；截面4和7也出现了相同的折射影响情况，即100 kPa下考虑折射影响的修正系数为1.27，而300 kPa下为1.23。

通过比较图13中不同围压下的曲线可得：① 试验初期，由于端部间隙和端部约束的影响，两种围压下的3个截面在轴向位移1 mm前的径向变形量几乎都为0。② 随着轴向位移的增加，100 kPa围压下截面7径向拟合圆的半径值出现下降，土样表现出体缩，截面4和2都表现为体胀，土样的不均匀变形开始出现。轴向位移达到一定加载阶段时，土样的上中下拟合圆半径均表现出增加，土样都表现为体胀。而300 kPa围压下的截面2、4的径向半径长度均为增值，表现为体胀。截面7折射修正前后的径向增量非常小，曲线类似于一条直线，说明土样上部在整个阶段几乎都没发生变化。③ 红黏土三轴不固结不排水试验中，土样的变形都表现出中间大两边小的鼓形破坏。④ 土样径向变形测量受折射影响比较大，利用光线追踪技术进行折射误差修正，得到修正系数为1.25。

由图13可知，以围压100 kPa下的截面4为例，试验2初始阶段，修正前半径长度是修正后的1.33倍；试验结束时，径向长度被放大1.35倍。通过对比截面2、 4的径向放大倍数，综合确定100 kPa围压下折射修正系数为1.34，300 kPa时为1.30。

通过比较图13中不同围压下的曲线可得：① 试验初期由于砂土样不够致密，围压100 kPa下的土样出现剪缩，围压300 kPa下的土样表现出体缩，导致各层变化都呈现截面径向长度减少；② 随着试验进行，不同围压下的砂样逐渐压密，土样3个部位均表现出剪胀现象，但截面2和截面7径向长度增大幅度较小，截面4径向长度增大幅度较大，猜测这是由于端部约束的影响导致整体表现出鼓状变形。③ 试验中后期，土样各部位变形曲线放缓，端部相比中部出现“平台”期，且随之各部位都出现变形曲线的反复直至表现出体胀现象，最终土样鼓状破坏。④ 折射对于土样径向变形的影响较大。但各截面修正前后曲线趋近平行，折射的影响一致，可以通过确定折射修正系数为1.32进行处理。

6 结 论

（1） 通过光线追踪原理建立的三维折射修正模型能有效消除压力室壁和密闭介质引起的折射放大效应。红黏土经修正后的轴向及径向测量值平均误差分别为0.118 mm和0.117 mm，砂土经修正后的轴向及径向测量值平均误差分别为0.131 mm和0.139 mm，满足试验所需。

（2） 通過对比红黏土和砂土的变形发现：折射效应对不同土样的轴向变形测量影响可忽略，但对不同土样的径向变形测量影响显著，红黏土样在径向上被放大1.25倍而砂土样被放大1.32倍。因此对不同土样不能做归一化处理，应考虑折射的实际影响，计算其相对应的折射修正系数。

（3） 经折射修正模型获取的土样变形值与实际值相吻合。本文修正方法可有效克服常规三轴试验的缺陷，为今后的三轴土样测量提供了一种新的思路。

参考文献：

［1］ 孙莉萍，杨玉春，刘槊.土工直接剪切试验和三轴剪切试验优缺点及适用范围［J］.水利水电工程设计，2013，32（4）：40-42，47.

［2］ 张克恭，刘松玉.土力学［M］.北京：中国建筑工业出版社，2010.

［3］ 姜朔.含软弱面膨胀土三轴试验结果的校正问题［J］.桂林理工大学学报，2013，33（2）：283-286.

［4］ 刘潇.三轴试验土样全表面变形测量方法及其应用［D］.大连：大连理工大学，2012.

［5］ LI L，LI P，YANG C，et al.Visualization of non-uniform soil deformation during triaxial testing［J］.Acta Geotechnica，2021，16：3439-3454.

［6］ 陈超斌，武朝军，叶冠林，等.小应变三轴试验方法及其在上海软土的初步应用［J］.岩土工程学报，2015，37（2）：37-40.

［7］ MALIK B，PIERRE D，SIAVASH G，et al.Drained triaxial tests in low-permeability shales：application to the Callovo-Oxfordian Claystone［J］.Rock Mechanics and Rock Engineering，2018，51（7）：1979-1993.

［8］ 刘港.基于全表面测量的三轴土样剪切破坏过程研究［D］.大连：大连理工大学，2017.

［9］ 黄永诚.数字图像测量方法在工程应用中的关键技术［J］.工程建设与设计，2017（5）：38-39.

［10］ 付玮.基于数字图像测量系统的标定与表面数据融合算法研究［D］.南昌：南昌大学，2018.

［11］ BHANDARI A R，POWRIE W，HARKNESS R M.A digital image-based deformatoion measurement system for triaxial test［J］.Geotechnical Testing Journal，2012，35（2）：209-226.

［12］ ZHANG X，LI L，CHEN G，et al.A photogrammetry-based method to measure total and local volume changes ofunsaturated soil during triaxial testing［J］.Acta Geotechnica，2015，10（1）：55-82.

［13］ HORMDEE D，KAIKEERATI N，JIRAWATTANA P.Application of image processing for volume measurement in multistage triaxial tests［J］.Advanced Materials Research，2014，931-932：501-505.

［14］ RECHENMACHER A L，MEDINA-CETINA Z.Calibration of soil constitutive models with spatially varying parameters［J］.Journal of Geotechnical and Geoenvironmental Engineering，2007，133（12）：1567-1576.

［15］ 王鹏鹏，郭晓霞，桑勇，等.基于数字图像相关技术的砂土全场变形测量及其DEM数值模拟［J］.工程力学，2020，37（1）：239-247.

［16］ 邵龙潭，阎崇超，曾飞涛.土工平面应变仪压力室的改进［J］.岩土力学，2017，38（5）：1251-1266.

［17］ 卢官明，陈浩，肖鲁宁，等.全景视图泊车辅助系统中的多视点视频拼接［J］.南京邮电大学学报，2016，36（3）：10-17

［18］ 李佳莹，罗哉，江文松，等.基于交比不变性的分区域相机畸变矫正［J］.中国测试，2020，46（9）：125-130.

［19］ 周子良.基于摄影测量的三轴土样变形特征研究［D］.桂林：桂林理工大学，2020.

［20］ 牟春梅，杨警，等.基于图像技术的三轴土样径向变形测量［J］.科学技术与工程，2021，21（27）：11712-11718.

（编辑：郑 毅）

Application of three-dimensional refraction correction model in soil sample deformation measurement

YE Kai1，XIA Yi，1 MOU Chunmei1，2

（1.College of Civil Engineering and Architectural，Guilin University of Technology，Guilin 541004，China； 2.Key Laboratory in Geotechnical Mechanics and Engineering，Guilin 541004，China）

Abstract：

With regard to the photogrammetry in triaxial tests，the refraction amplification effects from pressure chamber and different media exert great influences on the accuracy of photogrammetry results.In order to investigate the sensitivity of soils with completely different engineering properties to the refraction effect，this study selected the representative Guilin red clay and a general sandy soil as test materials，then a three-dimensional refraction correction model was established based on ray tracing technology.The deformation value of the soil sample directly obtained by photogrammetry was taken as a pre-corrected value of refraction，while the eliminated-refraction deformation value of the soil sample was taken as a post-corrected value of refraction.The axial deformation value and radial deformation value were incorporated as the influencing indexes to study the effect of refraction.By examining the deformation values of the two soil samples，the following results were obtained：① The influence of refraction effect on the axial deformation of the two soil samples was slight，yet the radial deformation played an amplifying role，making the red clay deformation amplified 1.25 times in the radial direction，and the sandy soil deformation amplified 1.32 times；②When the photogrammetry method was applied to the triaxial test deformation measurement，the refraction for different soil samples cannot be corrected by a fixed correction factor.In this case，the engineering characteristics of different soil samples should be considered，and different refractive correction coefficients should be given.

Key words：

triaxial test；refraction amplification effect； ray tracing；three-dimensional refraction correction model；photogrammetry