考虑建基面的沥青混凝土心墙坝竣工期沉降计算

杜成斌 王作彤 黎亚生 曹庆明 江守燕 杜乐

摘要：

为探究不同建基面形状对沥青混凝土心墙坝竣工期沉降的影响，采用邓肯-张非线性模型对轿子山沥青混凝土心墙坝的竣工期坝体沉降进行了计算。对比依据轿子山大坝实际剖面简化而来的理想算例以及不同坝高的其他典型工程计算结果，发现在数值模拟中计算大坝的最大沉降占比时，应该使用修正后的坝高，即总坝高减去心墙向下延伸的高度，且坝高90～140 m范围内最大沉降比与坝高之间为线性关系。为了进一步验证上述发现的普遍性，又对理想坝型研究了不同坝体建基面形状与心墙及过渡层（向下）延伸段对坝体沉降的影响。结果表明：在相同坝高下，坝体与基岩的交界面与水平方向的夹角越大，坝体最大沉降越小，从基岩受力变形角度初步解释了坝体沉降变化的原因，即是侧向分担了部分坝体自重；心墙及过渡层延伸段的存在会使坝体最大沉降略有减小，但延伸段高度及倾角的变化对坝体沉降的变化影响不明显。建议在坝基开挖的过程中，尽量使上下游建基面与水平面间保持一个尽可能大的夹角，同时将心墙及过渡层向坝基深处延伸一段距离。研究成果可供沥青混凝土心墙坝工程设计和施工参考。

关 键 词：

沥青混凝土心墙坝； 建基面形状； 坝体最大沉降； 邓肯-张模型

中图法分类号： TV 314

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.07.018

0 引 言

沥青混凝土心墙堆石坝作为典型的土石坝坝型，因其具有诸多优点而受到坝工界的青睐。它与同属于土石坝的混凝土面板堆石坝和黏土心墙堆石坝相比，适应坝基和坝体变形的能力更强，受气候环境和海拔高度等施工条件影响也更小。沥青混凝土心墙具有良好的防渗性、抗老化性、耐久性、自愈性、抗震性、延展性和温敏性等特点，而且可充分利用当地材料作为上下游坝体的坝壳料，具有很好的经济性［1-3］。截至目前，一批具有代表性的百米级高沥青混凝土心墙堆石坝在国内已建成使用：2003 年建成的坝高104 m的三峡工程茅坪溪沥青混凝土坝［4］，2005年四川建成的高124.5 m的冶勒沥青混凝土坝［5］，2013年新疆建成的坝高106 m的石门沥青混凝土坝等［6］，这些大坝至今运行良好，发挥了巨大的经济效益和社会效益。

竣工期坝体的沉降及其分布规律一直是沥青混凝土心墙坝研究过程中的关键问题之一［7］。通常情况下坝体的最大沉降比是衡量堆石坝施工期变形的重要参数。对于百米级坝而言，竣工期的坝体沉降一般表现为上下游整体对称，最大沉降出现在坝高1/2～1/3的坝轴线（一般为心墙）附近，占最大坝高的1%左右［7-10］。但对不同的坝高，合理数值究竟多少，以及大坝建基面形状对坝体沉降的影响等方面，很少有相关研究。本文针对这些问题，以轿子山水库沥青混凝土心墙坝以及国内其他典型沥青混凝土心墙为例展开探讨。

1 材料计算模型

现有沥青混凝土心墙坝的计算大多采用邓肯-张模型，尽管它不能描述粗粒料的剪胀性和剪缩性，但因其能较好地反映坝体材料和沥青混凝土的非线性状态，且概念清楚，使用方便，因此在沥青混凝土心墙坝的计算分析中一直得到广泛的应用［11-14］。

2 轿子山大坝峻工期沉降计算

2.1 工程概况

轿子山水库地处昆明市东川区红土地镇境内，位于金沙江流域小江左岸一级支流小清河中游，属金沙江水系二级支流。拦河大坝为沥青混凝土心墙风化料坝，其基本剖面见图1。坝顶轴线长320 m，最大坝高99.0 m，坝顶高程2 204.00 m，坝顶宽10.0 m；水库正常蓄水位2 201.50 m，死库容315万m3，兴利库容1 635万m3，总库容2 033万m3。依据地震安全评价的结果，坝址场地地震基本烈度8度，水平地震动峰值加速度0.26g。尽管河谷形状对大坝的变形会有影响，但本文主要研究竣工期心墙坝的最大沉降比规律，因而选择大坝的最大断面位置（此处一般也是沉降最大的断面）作为研究对象。

2.2 施工模拟

本次计算中，坝基沿着上下游及深度方向各延伸约3倍坝高的长度，对大坝采用逐级加载的形式模拟施工过程，第1级为坝基，2～5级为上游度汛坝体，6～15级为筑坝过程。研究表明，对于百米级土石坝，当分层数达到10层左右时，可满足计算精度要求［15］，故对轿子山大坝计算模型取约10 m一级的高度進行逐级加载，具体过程如图2。计算采用的有关参数见表1，其中堆石料和沥青混凝土的有关参数根据相关试验确定，过渡料的参数是根据施工期实测的心墙变形、坝基沉降反复试算获得的。地基视为线弹性，弹性模量E=20 GPa，泊松比ν=0.3。

2.3 坝体沉降计算结果

轿子山坝典型断面竣工期的坝体沉降分布如图3所示，上下游坝体沉降整体对称，最大沉降出现在坝高1/2～1/3的心墙附近，规律上符合一般百米级沥青混凝土心墙坝的特点，而最大沉降与坝高的比值为0.47%。下文将对该比值的合理性进行分析，并提出建议修正计算方法。

3 理想算例及不同坝高的沉降计算规律

3.1 理想算例设计

参考国内类似典型大坝的典型断面［7，9，10，16］，将轿子山大坝的基本剖面进行简化，坝顶宽度取10 m，心墙厚度为1 m，两侧过渡层厚度3 m，上下游坡比为1∶2的理想模型。计算模型如图4所示，有限元网格剖分详见图5。不同坝高的理想算例上、下游坡比均为1∶2。

3.2 不同坝高的沉降计算规律

算例1（100 m坝高）沉降计算结果见图6。由图可知，坝体沉降分布情况合理，符合一般规律，最大沉降出现在坝高1/2～1/3处，值为65.35 cm，沉降约占坝高的0.65%。后续分别对90，110，120，130，140 m的算例进行计算，发现不同坝高下，坝体的沉降分布规律基本与算例1一致，但最大沉降与坝高的比值随坝高增大而增大，坝高140 m时达到1.05%，具体结果见表2。

3.3 理想算例计算与国内实际工程对比

因理想算例的计算结果中最大沉降与坝高的比值与坝高之间近似为线性关系（表2），故将其拟合为直线，拟合后的直线方程为y=0.0101x-0.3815，其中y为最大沉降比，x为坝高（m）。将之与国内典型百米级沥青混凝土心墙坝已有的沉降计算结果［7，9，10，16，17］（表3）进行对比。结果显示，工程实例计算结果的样本点半数贴近理想算例计算结果的拟合直线（图7），而轿子山、石门、官帽舟3个样本点离散较为明显；考虑到理想模型由轿子山实际剖面简化而来，主要差别在于理想模型“抹平”了心墙及过渡层向下延伸的一部分（12 m），如果将各样本中心墙及过渡层向下延伸的高度从总坝高中扣除，并重新计算最大沉降与修正后坝高的比值后发现，离散的样本点基本分布在拟合直线的两侧且较为贴合。这说明在数值模拟中计算最大沉降占比时，应该使用修正后的坝高，即总坝高减去心墙向下延伸的高度，同时也说明轿子山、石门、官帽舟计算结果同样合理，进而说明本次计算采用的计算模型也是合理的。

4 坝体基岩交界面与水平面间夹角对坝体沉降的影响

当大坝典型断面的坝体基岩交界面基本为一条水平线时，可将大坝断面近似为一个梯形断面。但实际上，如黄金坪［18］等工程的典型断面中，坝体与基岩的交界面相对于水平面间存在夹角（见图8），当该夹角较大时，断面便不能直接近似为一个梯形断面。所以，有必要进行同一坝高下不同夹角对坝体沉降影响情况的分析。

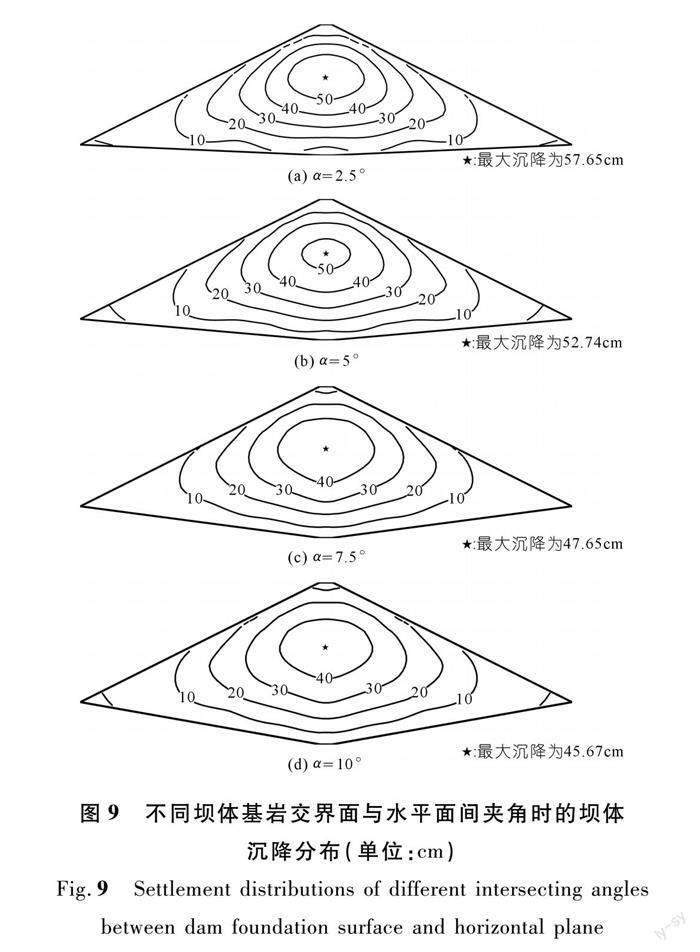
以算例1（α=0°）为参考，在保持坝高不变的情况下，分别取α=5°，10°，15°，20°进行坝体沉降的计算，结果如图9和表4所示。结果表明，坝体基岩交界面与水平面间夹角对坝体沉降的分布规律影响不明显，但对坝体最大沉降值有着较为明显的影响：随着夹角的增大，坝体的最大沉降值不断减小，且夹角越小时，坝体最大沉降减小得越快。从受力分析上来说（见图10），原先作用在水平面的重力G全部由基岩底部边界承受，但由于夹角α的存在，会产生一个垂直于建基面（侧向偏下）的力G cosα，而这部分力则由基岩侧向边界来分担，使得竖向沉降有所减小。

5 心墙及过渡层向地基延伸对坝体沉降的影响

许多实际工程的典型断面中，由于地质条件限制，常会出现心墙及过渡层底界比其他坝体部分多向下延伸一定高度的情况，暂称这一部分为延伸段，如图11所示。延伸段的倾角约在30°～70°，高度在几米到十几米不等［7，16，19，20］，且该部分的高度往往会被计入总坝高之内。先前的分析中，在考虑沉降占比的合理性时，将延伸段高度直接从最大坝高中扣除作为修正的坝高，未考虑延伸段具体尺寸变化带来的影响，故这里有必要对延伸段对坝体沉降的影响进行进一步的研究。

5.1 延伸段的高度对坝体沉降的影响

为研究延伸段的高度h对坝体沉降的影响，在取延伸段倾角β为60°的情况下，高度h分别取1，3，5，10，15 m进行计算。计算结果见表5。结果显示，随着延伸段的高度h增大，坝体最大沉降值随之增大，但影响不明显。

5.2 延伸段的倾角对坝体沉降的影响

为研究延伸段的倾角β对坝体沉降的影响，在取延伸段高度h为10 m的情况下，对倾角β分别取30°，40°，50°，60°，70°，80°进行计算，计算结果见表6。结果显示，随着倾角β增大，坝体最大沉降值随之减小，但影响同样不明显。

总之，当坝体心墙及过渡层部分存在向下的延伸段时，坝体的最大沉降值会有所减小，初步认为其减小的原因与图10中的坝体断面受力类似，且改变延伸段倾角或高度对结果影响不明显。

6 结 论

在不改变大坝断面整体形状的情况下，随着坝高的增大，坝体整体沉降规律不会发生明显变化，但最大沉降与坝高的比值会随之增大，且发现最大沉降比与坝高之间关系近似为一直线。在数值模拟中计算最大沉降占比时，应该使用修正后的坝高，即总坝高减去心墙延伸段高度；在同一坝高下，坝体与基岩的交界面相对于水平面间的夹角发生改变时，坝体沉降也会受到影响，具体表现为随着夹角的增大，坝体的最大沉降值不断减小，且夹角越小时，坝体最大沉降减小得越快，这种变化的主要原因是夹角的存在使得基岩侧向承受一定的坝体自重。当坝体心墙及过渡层部分存在向下的延伸段时，坝体的最大沉降值会略有减小，但延伸段傾角或高度的改变对坝体沉降的影响不明显。建议在坝基设计和施工中，在开挖量许可的条件下，上下游建基面与水平面间保持一个尽可能大的夹角，可减少坝体最大的沉降。

参考文献：

［1］ 李江，柳莹，何建新，等.新疆高沥青混凝土心墙坝建设关键技术与应用［J］.水利水电技术，2021，52（11）：85-97.

［2］ SEO J W，PARK D W，LE T H M.Development of an asphalt concrete mixture for Asphalt Core Rockfill Dam［J］.Construction and Building Materials，2017，140：301-309.

［3］ 杨启贵，孔凡辉，万云辉，等.卡洛特水电站枢纽布置设计［J］.人民长江，2022，53（2）：132-137.

［4］ 杜治华.三峡水利枢纽茅坪溪防护大坝应力与变形的分析和预测［D］.武汉：武汉理工大学，2002.

［5］ 曹学兴，何蕴龙，熊堃，等.汶川地震对冶勒大坝影响分析［J］.岩土力学，2010，31（11）：3542-3548.

［6］ 李江，柳莹，何建新.新疆碾压式沥青混凝土心墙坝筑坝技术进展［J］.水利水电科技进展，2019，39（1）：82-89.

［7］ 崔娟，沈振中，凌春海.官帽舟沥青混凝土心墙混合坝应力变形分析［J］.水电能源科学，2008（2）：78-81.

［8］ 朱晟，曹广晶，张超然，等.茅坪溪土石坝安全复核［J］.水利学报，2004，48（11）：124-128.

［9］ 汪明元，周欣华，包承纲，等.三峡茅坪溪高沥青混凝土心墙堆石坝运行性状研究［J］.岩石力学与工程学报，2007，26（7）：1470-1477.

［10］ 刁志明，邓弟平，廖秀峰.金佛山沥青混凝土心墙坝有限元应力变形分析［J］.水电能源科学，2013（5）：55-58.

［11］ 张芸芸，陈尧隆，吕琦，等.沥青混凝土心墙坝的应力及变形特性［J］.水资源与水工程学报，2009，20（3）：87-90.

［12］ BI Q T，DING S Y，JIA J C.Stress and deformation characteristics of asphalt concrete core dam on deep overburden layers［J］.Applied Mechanics & Materials，2013，438-439：1359-1362.

［13］ LIU C，ZHANG L，BAI B，et al.Nonlinear analysis of stress and strain for a clay core rock-fill dam with FEM［J］.Procedia Engineering，2012，31：497-501.

［14］ 王相峰，唐新軍，胡小虎.浇筑式沥青混凝土心墙坝心墙性态的有限元分析［J］.人民长江，2013，44（1）：82-85，93.

［15］ 江德军，黄会宝，柯虎，等.土石坝填筑数值模拟中分层数影响研究［J］.人民长江，2015，46（增1）：130-131，136.

［16］ 何顺宾，胡永胜，刘吉祥.冶勒水电站沥青混凝土心墙堆石坝［J］.水电站设计，2006，22（2）：46-53.

［17］ 程瑞林.新疆呼图壁河石门沥青混凝土心墙砂砾石坝设计［C］∥中国大坝协会.中国大坝协会2014学术年会论文集.北京：中国大坝协会，2014：153-160.

［18］ 嵇红刚.深厚覆盖层上沥青混凝土心墙堆石坝三维动力分析［D］.南京：河海大学，2006.

［19］ 张生财，霍礼锋，周亮.阿拉沟水库防渗体系设计与研究［J］.水利水电技术，2016，47（3）：16-20.

［20］ 吾提库尔·胡斯曼.浅谈强夯在吉尔格勒德水利枢纽工程坝基处理中的应用［J］.中国水运（下半月），2018，18（7）：166-167.

（编辑：郑 毅）

Settlement calculation of asphalt concrete core wall dams at end of construction period considering foundation plane shape

DU Chengbin1，WANG Zuotong1，LI Yasheng2，CAO Qingming2，JIANG Shouyan1，DU Le1

（1.Department of Engineering Mechanics，Hohai University，Nanjing 211100，China； 2.Yunan Provincial Investigation，Design & Research Institute of Water Conservancy & Electric Power，Kunming 650021，China）

Abstract：

In order to investigate the influence of dam foundation plane shape on dam settlement at the end of construction period of asphalt concrete core wall dams，Duncan-Chang nonlinear model was used to calculate the settlement of the Jiaozishan weathered asphalt concrete core wall dam based on ABAQUS platform.A benchmark model was designed according to practical profiles of Jiaozishan project.After comparing the calculation results of Jiaozishan dam with several similar projects with different dam heights，it was found that a modified dam height should be adopted when calculating the maximum settlement proportion of dams in numerical simulations，that is，the total dam height minus the height of the core wall extending downward，and the relationship between the maximum settlement ratio and the dam height is linear for dams heights of 90～140 m.Furthermore，the influence of foundation plane shape and the downward extension sections of core wall and the transition layer on the settlement of the dam body was studied.The results show that under the same dam height，the larger the angle between the interface of dam and foundation and the horizontal plane，the smaller the maximum settlement of a dam.This phenomenon is explained from the point of bedrock deformation，as part of the weight of dam body is laterally shared by bedrock.The downward extension sections of the core wall and the transition layer will reduce the maximum settlement of the dam slightly，but variation of height and inclination angle of the extension section has no obvious influence on the maximum settlement of the dam.It is suggested that in the excavation of dams foundation，the angle between upper and lower foundation planes and the horizontal plane should be as large as possible，while the extension sections of transition layer and core wall should extend downward for a certain distance，which can reduce the maximum settlement of the dam body.The results can be used as reference for engineering design and construction of asphalt concrete core wall dams.

Key words：

asphalt concrete core wall dam；foundation plane shape；maximum settlement of a dam；Duncan-Chang model