基于改进DIIM的洪涝灾害下供应链系统中断关联型损失评估研究
王 婷,仇 蕾,汪志强,支彦玲
(1.河海大学管理科学研究所,江苏 南京 211100; 2.浙江财经大学信息管理与人工智能学院,浙江 杭州 310058;3.常州大学商学院,江苏 常州 213159;)
近年来,极端天气频发,暴雨洪涝灾害给社会经济带来严重危机,全球的供应链网络面临着极大的挑战,如2022年西欧和中国河南的严重洪涝灾害对全球供应链构成威胁,极端洪水破坏了这两个区域的货物及原材料运输线路,严重损坏了工业区内的生产设施和仓库。2022年5月23日,中华人民共和国国务院常务会议强调:“疫情和洪涝灾害等对生产的连续性形成一定影响,各方须争分夺秒抓落实,尽可能缩短政策时滞,提升政策效能,为企业应对风险、抓住机遇争取更多主动”。由洪涝灾害造成的供应链中断问题层出不穷,给经济发展带来了极大的困扰,因此有必要对洪涝灾害下供应链系统的弹性及洪涝灾害造成的关联损失进行全面评估,以便为洪涝风险管理提供参考。
目前,洪涝灾害导致的供应链损失评估模型主要包括生产函数模型、一般均衡模型、投入产出及其扩展模型等,其中投入产出模型由于所需数据量小、计算方便,比其他模型得到了更广泛的普及和发展,主要有经典投入产出模型(input-output model, IOM)、非正常程度投入产出模型(inoperability input-output model,IIM)和动态非正常程度投入产出模型(dynamic inoperability input-output model, DIIM)。1952年,Leontief[1]采用经济数学模型方法研究了复杂系统中不同部门或产品数量上的关联关系。Ghosh[2]于1958年提出IOM的对偶模型,即供应驱动的IOM。随后,Jiang等[3]从美国经济分析管理局公布的投入产出表中选定了12个重要的投入产出行业,利用IOM展示了如何通过合理利用人力资源最优配置的方式来有效减少经济损失。Haimes等[4]对传统的IOM进行了改造,提出了需求驱动下的IIM,研究了基础设施系统间的经济关系。Lian等[5]提出供应驱动的静态IIM,之后Xu等[6]将供应驱动的静态IIM进一步发展,提出供应驱动的动态输入输出模型DIIM,并用于解决供应链方面的问题。在此基础上,Liu等[7]利用DIIM对COVID-19 中供应链复杂网络的欠载级联故障和缓解策略进行建模,Jabilles等[8]基于供给侧DIIM模拟了库存对供应链弹性的影响,郑德权等[9]构建两阶段动态IIM,评估危机事件发生后对经济系统中具有关联关系的各部门的经济影响。王娅楠等[10]以一个物流服务作为基础集成商,在多个功能型物流服务的共同作用下,利用DIIM建立了物流协调调度模型。综上所述,DIIM是IOM不断发展的产物,相比IOM,DIIM可以描述中断发生后几天至几个月内灾害对供应链的影响过程,便于分析洪涝灾害造成的影响在供应链系统上的传播情况,而这种影响在供应链系统中传播的根本原因就是供应链中各个节点之间存在着关联关系。因此,本文引入对关联系统有很强适应性的DIIM并对其进行改进,用于评估供应链系统的损失,以期为管理者制定减灾策略提供依据。
1 相关概念及基础理论
1.1 供应链非正常程度概念
非正常程度是DIIM模型的核心概念,是指由于受到某种干扰,使系统在无法达到自身期望功能水平时所表现出来的整个系统非正常运转的一种状态。由于各个供应链节点间复杂相互关联关系,扰动对任一企业节点的直接袭击都极有可能会致使初始非正常程度沿着整个供应链网络的方向传递到其他企业节点,从而对供应链产生影响,造成整个供应链系统非正常程度的上升,有可能会直接引发整个供应链系统瘫痪或崩溃。供应链DIIM是分析供应链系统复杂关系的有效参考工具,可模拟由洪涝灾害扰动导致供应链非正常程度随持续时间推移而变化的过程。
1.2 洪涝灾害对供应链非正常程度影响
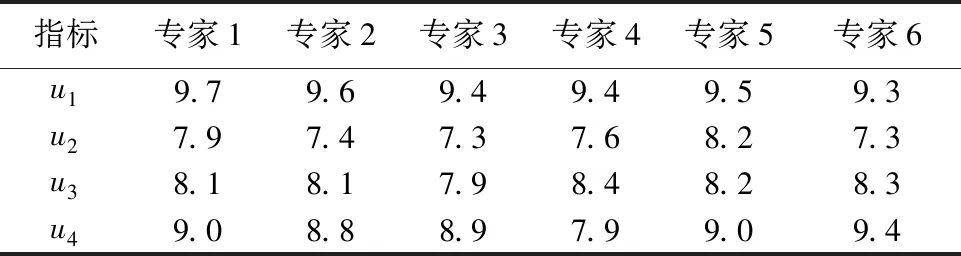
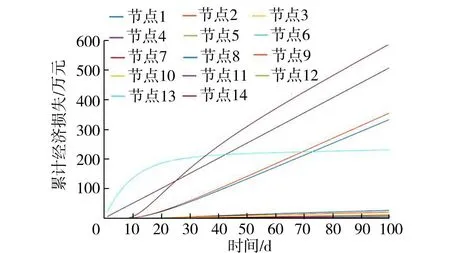
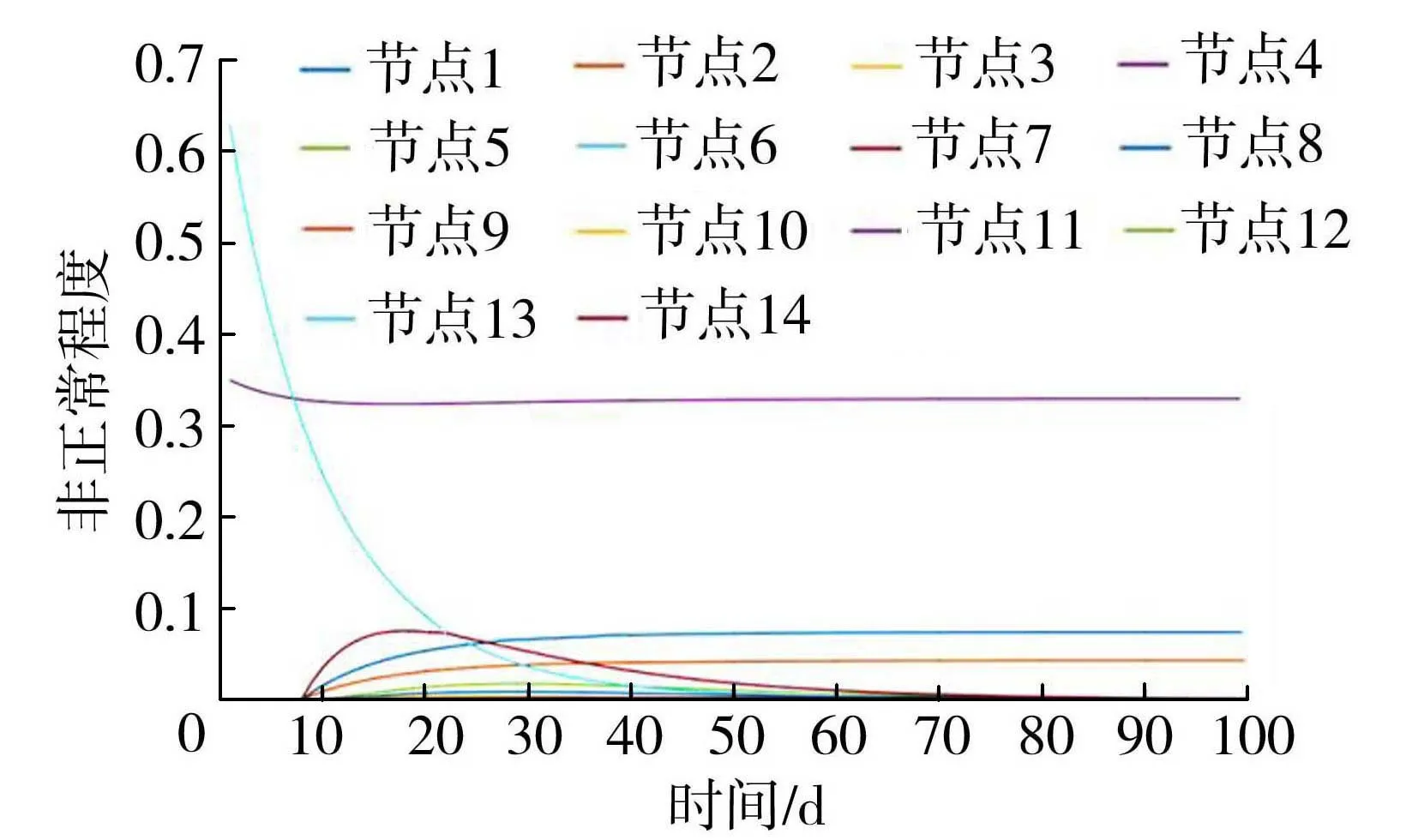
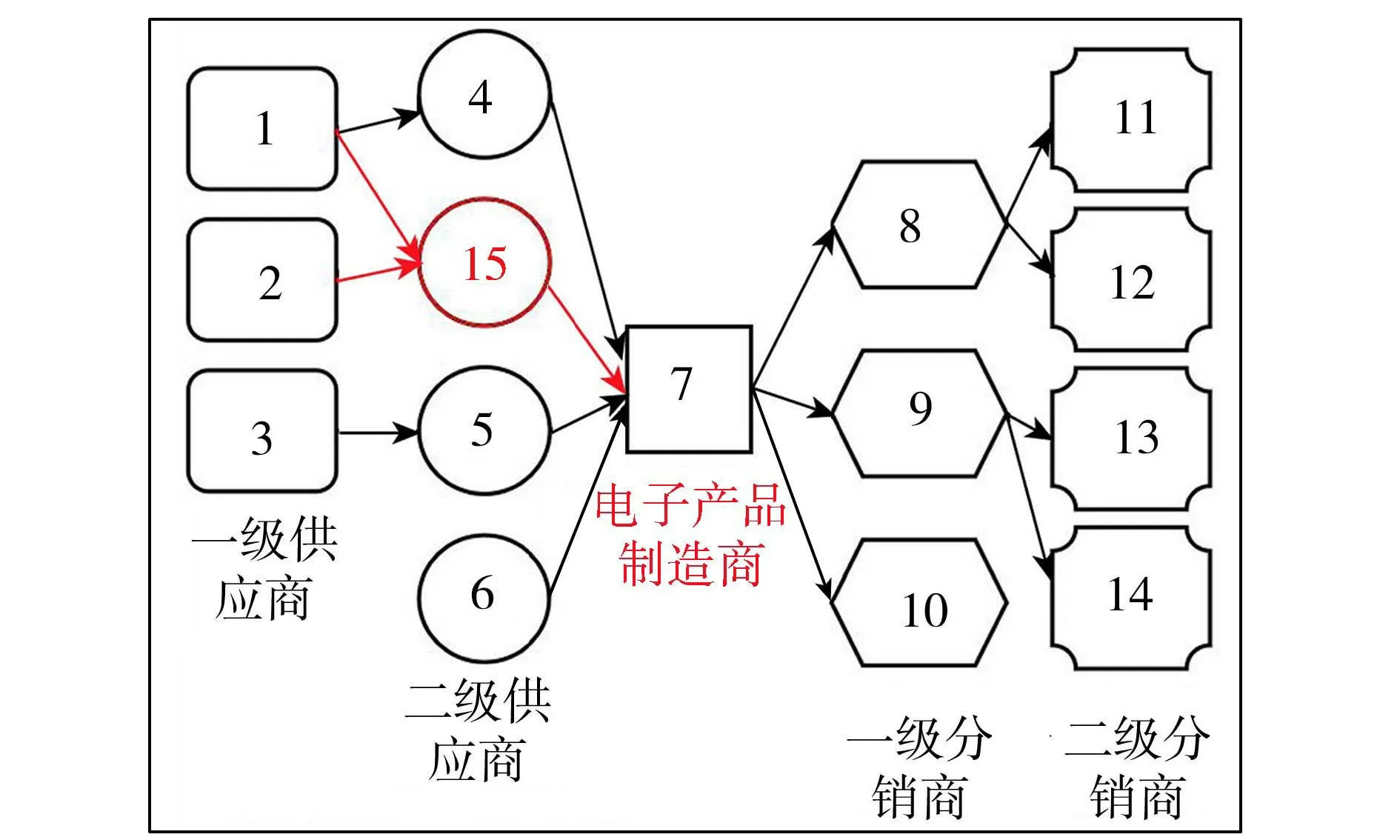
由于供应链节点之间存在着复杂的联系,洪涝灾害发生之后风险会在系统中快速传导,供应链系统功能下降,并给关联企业带来连带损失。供应链非正常程度变化曲线如图1所示,它的变化性往往经历了4个阶段: 0 图1 洪涝灾害下供应链非正常程度变化曲线 传统DIIM是一种可以用来动态分析宏观经济管理系统中各部门相互关联关系和计算投入产出的有效工具[11]。作为相对微观的经济系统,供应链的子系统是某个企业节点,而不是某一行业,因此,供应链DIIM较传统DIIM在参数的定义与数据获取方式等方面需要进行部分调整。本文以洪涝灾害为背景,根据供应链特点,设定相关假设和参数,将洪涝事件引发的扰动信息输入供应链DIIM中,由此建立起适用于供应链系统的DIIM损失评估模型。 DIIM是IIM的动态版本,DIIM的主要贡献是能够动态地对恢复轨迹进行建模,并说明在一个时期内的非正常程度如何影响下一个时期的生产。模型方程[12]为 (1) (2) pt+1=pt+K(A*pt+zt*-pt) (3) 式中pt+1为t+1时刻的非正常程度。将可获得的数据代入该公式中,由此可得到供应链各节点的非正常程度及其随时间的动态变化情况,各节点非正常程度可作为评估供应链中断情况的指标之一。 常见的计算供应链间相互关联矩阵的方法是有序加权平均算子法(ordered weighted averaging,OWA),但权重设定相对主观,本文运用灰色模糊法改进OWA[13],以某节点为例,具体步骤如下: 步骤1令U=(u1,u2,u3,u4)有n个待评价的节点,各指标的权重未知,但权重之和为1。节点i在指标ui下规范化的值为rij,rij为在论域[0,1]上的灰色梯形模糊数。 步骤2建立灰色模糊评价矩阵,根据梯形模糊数运算法则[14],采取比重变换法做规范化处理。 步骤3将准则值转化为实数。利用F-OWA算子和C-OWA算子[15]分别将矩阵中灰色模糊数的模部和灰部转化为实数,转化后的矩阵D=[qijdijFdijG]4×n,其中qij为rij的模部由F-OWA算子转化来的实数,dijF为rij的灰部由C-OWA算子转化来的实数,dijG为表示模糊程度的模糊数。 步骤4在灰色模糊矩阵的基础上利用OWA对各评价指标赋权,针对评价指标ui给出评价数据(a1,a2,…,ak)。对评价数据从大到小排序,用组合数对某数据cj赋权,进而得到评价指标ui对应的赋权向量: (4) 式中k为评价数据总量。 步骤5通过赋权向量对决策数据加权,得到指标ui的绝对权重wi,进而计算相对权重Wi: wi=∑eicj (5) (6) 步骤6利用式(7)(8)得到实数型评价值,再将实数型评价值加权得到各节点的综合评价值: Zij=qijdijF(1-dijG) (7) (8) 重复以上步骤得到相互关联系数矩阵A*,在遭受冲击后、采取措施前的这段较短的时间内,可认为相互关联系数保持稳定,因此这里假设当供应链中断发生时,节点间相互关联关系是稳定不变的。 设定企业节点非正常程度和供应链中断造成的经济损失之间的关系是线性的,由于供应链中断后各企业节点的非正常程度是一个动态变化的过程,则各节点每天所产生的经济损失也是动态变化的,考虑时间变量,在一定时期内,每个节点i的累计经济损失由下式给出: (9) 对于整个供应链而言,n个节点的总经济损失Qt的计算公式为 (10) 某电子产品制造商是全球知名的跨国企业集团,其供应链遍布全球,马来西亚的工厂提供了该企业所需的电子元件和半导体材料。2021年,马来西亚遭遇严重洪涝灾害,造成重大人员伤亡和经济损失。洪水导致该电子产品制造商遭受电子元件和半导体材料供应严重短缺。本文以该电子产品制造商的供应链为基础,进行了仿真分析。如图2所示,选取14个代表性节点,图中节点1~3为原材料供应商,即一级供应商;节点4为马来西亚半导体供应商;节点5为其他材料供应商;节点6为马来西亚电子元件材料供应商;节点7为该电子产品制造商;节点8~14为销售网络;供应链的中断发生在节点4和节点6。应用改进的DIIM来测算此次洪涝灾害所造成该供应链系统损失。 图2 某电子产品制造商供应链拓扑结构 当洪涝灾害发生时,从供需角度来讲,供应链遭受的扰动可能有两种情况,一是洪涝灾害发生时供应链需求端的扰动,即洪涝灾害下供应链末端对产品需求量的变动对供应链系统产生消极的影响;二是洪涝灾害发生时供应端的扰动,即受灾地区企业生产能力下降,供应不足而呈现的非正常程度增加。基于改进DIIM,节点4和节点6因受淹而产能下降,使得2条生产线直接受损,产能分别降低35%和63%; 节点中断致节点4无法给节点7正常供货超 3 个月,供应链末端需求能力下降,相当于节点4产品供给能力降低30%,将恢复系数设置为0.1,其余参数设置为0。马来西亚洪涝灾害造成工厂停工后,由于其他企业尚有多余的库存或者决策者已经采取了相关应对供应链中断的管理方案,使得在灾害发生后的几天里,其他节点尚未完全受到马来西亚洪涝灾害事件导致的断供因素影响,因此设置滞后时间为8d。根据仿真结果得到了随着时间的推移各节点非正常程度及损失的变化。 洪涝灾害导致供应链网络级联失效的原因是节点之间存在着复杂的联系,对节点的关联程度的衡量,需要根据洪涝灾害的特征,综合考虑节点在网络中的物理属性以及孕灾环境等多重因素。一方面,考虑到物流网络所具有的边权特征如物流节点间的运输距离差异会导致业务传输效率不同;另一方面,不同节点由于其服务功能和地理位置不同,洪涝灾害对其影响也有区别,如制造业比金融业更容易受到洪涝灾害的冲击。因此在研究洪涝灾害下供应链节点关联特征时,本文选取业务联系程度、业务可替代性、抗洪灾能力、备用库存水平4项指标。首先要求相关的供应链领域专家为与节点i直接相连的节点提供评估,包括确定每个定量因子的实际区间和每个定性因子的评级区间,评级从[1,10]中选择。业务联系程度指标为收益型属性指标,其他3个指标都为成本型属性指标,采用区间灰色模糊评价法来改进指标赋权方法[16],有效缓解了主观因素对结果的干扰,以此对物流节点的关联度进行综合度量。以节点7及其6个直接相关节点(4、5、6、8、9、10)为例,建立指标u1~u4对应的初始灰色模糊矩阵并规范化得到新的矩阵Mu1~Mu4:以指标u1的权重计算为例,首先对6个决策者的评价数据从大到小排序,即得到(9.7,9.6,9.4,9.4,9.5,9.3),根据式(4)得赋权向量ei=(0.03125,0.15625,0.31250,0.31250,0.15625,0.03125),根据式(5)得到绝对权重wi=(9.4531,7.5469,8.1969,8.9156),根据式(6)得到归一化的准则层权重向量Wi=(0.277 1,0.221 2,0.240 3,0.261 4)。由式(7)、式(8)循环运算得到节点7和其他直接关联节点4、5、6、8、9、10的相互关联系数为(0.183 4,0.1764,0.1256,0.1555,0.0766,0.0746)。对于存在竞争关系的节点,给定该节点在一段时间内与上一级供应商的供需数量,统计得出有相互竞争的节点和没有相互竞争的节点对供需数量的相互影响[17]。本文选取了6位专家,通过不断地重复以上步骤,便可以得到专家评级打分表(表1),以及该供应链中14个节点之间相互关联系数矩阵A*。 表1 针对评价指标的专家评级打分 (11) (12) (13) (14) 节点1~14的日均计划经济收益分别为53万、98万、79万、15万、28万、33万、103万、34万、72万、54万、58万、21万、62万、80万元,根据式(9)和式(10)可以算出各节点的每日累计经济损失以及供应链总经济损失。 如图3所示,由于洪涝灾害的影响,节点4和节点6生产失效并产生预期利润的损失,而供应链中其他节点正常的原料供应及产品生产活动受阻,也产生了关联损失。由于各节点最终的非正常程度由初始非正常程度和各节点初始增加值扰动共同决定,当节点6的生产能力恢复后,节点4引发的产品需求变动无法立刻回归原始水平,除与节点4无直接关联的节点6外,其他各节点的非正常程度持续增长到峰值后又稳定在某一固定水平,而不能完全恢复到初始状态。在这种情景下,除节点6外各节点在灾后损失维持上升状态,节点6受节点4初始扰动影响较小,最终损失稳定不再增加。节点7在100d内总经济损失达到589.5万元,最终,由于洪涝灾害造成的供应链100d内总经济损失达到2137.2万元,如图4所示。 图3 供应链各节点非正常程度随时间变化过程 图4 供应链各节点累计经济损失随时间变化过程 a.调整关联程度(不改变拓扑结构)。在改进DIIM的供应链关联损失评估模型中,供应链节点的相互关联程度由产品交易量、可替代性、产品缓冲供应商或产品分销商的缓冲库存数量和产品缓冲库存能力(包括备用缓冲库存)4个关键指标经过改进的OWA-灰色模糊评价法计算得出。所以,通过改变整个供应链系统的产品缓冲供应库存计划,可以改变供应链节点间的关联程度。通过优化供应,使得节点7对节点4的需求减少,对节点5的需求增加。假设节点7与节点4的关联系数减小到0,节点7与节点5的关联系数增大到0.3,通过仿真分析,可以得出供应链中断后的各节点非正常程度随时间的变化规律和整个供应链总经济损失如图5所示。从图5可以看出,这一措施对发生受淹企业(节点4、节点6)的非正常程度无显著影响,但节点4受淹时对节点7及下游企业的影响变小,100d内的总经济损失(1675.2万元)小于采取该措施前的结果(2137.2万元),可见通过调整供应链网络各成员之间的合作关系可以实现优化供应,达到减小供应链中断影响波及的效果,从而减少供应链中断损失。 图5 调整关联程度后的供应链各节点非正常程度随时间变化过程 b.增加备用供应渠道(改变拓扑结构)。如图6所示,当节点4受到冲击后,节点7暂停向供应商节点4订货,将订单交付其他备选供应商(节点15),来获取自身生产电子产品所需要的半导体。通过仿真分析,可以得出供应链中断后的各节点非正常程度随时间的变化规律和整个供应链总经济损失如图7所示。在图7中,当增加了供应商节点15时,除了节点4外,网络中的其他成员最终都能得到恢复,供应链整体中断损失得到显著减少,为873.2万元。由此可见多源供应是预防供应链中断的有效措施之一,在供应链中断发生后如果能及时找到新的替代品或供应商,被波及的企业也可以及时止损,且能在短期内恢复正常水平。 图6 增加备用供应渠道后的供应链拓扑结构 图7 增加备用供应渠道后的供应链各节点非正常程度随时间变化过程 c.采取自我恢复措施。在供应链节点受到洪涝灾害侵袭后,受灾企业可以通过采取租借受损设备、部分生产管理环节外包等自我恢复措施来提高恢复系数。而其被影响的供应链节点企业也同样可以通过及时改变设备采购方案以及调整销售策略等措施来提高自身在遭受供应链中断事件影响后的自我适应能力。恢复系数表示供应链中各个节点企业在供应链中断后的自我适应能力,即自我恢复能力。假设将节点4的恢复系数由0.1增大至0.5,通过仿真得到图8。图8中,通过增大中断节点4的恢复系数,虽然不能降低非正常程度峰值,但可以使节点4的非正常程度很快达到稳定状态,其他节点的非正常程度也会逐渐趋于稳定,供应链整体中断损失稍有减少,为2131.9万元。 图8 采取自我恢复措施后的供应链各节点非正常程度随时间变化过程 基于仿真结果可以看出,基于改进DIIM可以对各供应链节点及整个供应链在特定时间段内的经济损失情况作出综合评估,以便于企业和决策者制订相应的经济风险应对方案和措施。 a.供应链中断下各节点的非正常程度是由初始增加值的扰动和初始非正常程度,即需求端和供应端两方干扰共同影响,由于供应链的复杂性,影响的传递往往存在着时间滞后效应。非正常程度和损失是动态变化的,并呈现出一定的阶段性特征。 b.企业在应对供应链中断的问题上,可以从中断影响的阶段性出发,在每一阶段制定合适的策略,如通过优化供应,调节整个供应链中各个节点企业的关键指标以改变节点关联程度,通过增加备用供应商、寻求替代品等措施改变供应链结构,通过对受损设备的租借、部分生产管理环节外包等方法提高供应链节点企业自我恢复能力,而其被影响的供应链节点企业可以通过及时改变设备采购方案以及调整销售策略等措施来提高自身在遭受供应链中断事件影响后的自我适应能力。 c.算例仿真结果直观地显示了洪涝灾害事件下的供应链扰动和供应链中断影响的发生、扩散及恢复的过程,并进一步将供应链减损的措施和DIIM损失评估模型有机结合,为企业正确处理供应链网络的中断问题提供了理论依据,便于决策者根据供应链系统所受影响的程度和阶段性特征对关键节点进行管理。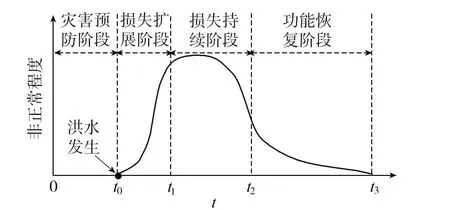
2 模型建立及算法描述
2.1 模型构建
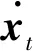
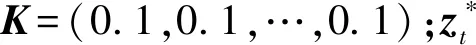
2.2 供应链节点关联矩阵改进算法
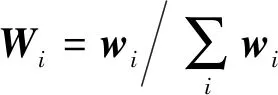
2.3 基于改进DIIM的供应链关联损失评估
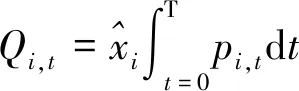

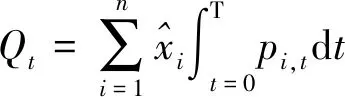
3 算例仿真研究
3.1 算例设计

3.2 供应链节点关联矩阵计算
3.3 仿真结果分析

3.4 减灾策略模拟

4 结 论

