基于三角形网格的无量纲最小二乘有限元法及其应用

李浩, 宋艳争, 刘刚*, 吕金潮, 靳立鹏, 武卫革

(1.华北电力大学(保定)电气与电子工程学院, 保定 071003; 2.国网冀北电力有限公司技能培训中心, 保定 071051;3.保定天威保变电气股份有限公司河北省输变电装备电磁与结构性能重点实验室, 保定 071056)

油浸式变压器是电力系统中最重要的设备之一,其在电力系统中扮演着重要角色。油浸式变压器的绝缘老化主要受温升影响,油浸式变压器温升与油流速度是一种强耦合关系[1],油流速度的大小直接影响着温升。油浸式变压器在运行中油流不可避免的存在着气泡,而油流速度又会影响气泡移动从而影响变压器的击穿特性[2]。当油浸式变压器使用瓦斯保护时,往往由于油流涌动存在着误动的情况,对于油浸式变压器出口油流速度与压力的监控显得尤为重要[3]。由此可看出,准确计算出油浸式变压器油流速度对其运行、继电保护及使用寿命具有重要的研究意义。

目前,流场数值计算方法主要有有限体积法和有限元法。邓永清等[4]基于自适应网格的有限体积法对油流速度进行了计算,减小了计算误差并提高了计算效率。魏本刚等[5]基于有限体积法对三维变压器冷却问题进行了研究。Mufuta等[6]采用有限体积法求解了大型变压器盘型绕组速度分布。然而采用有限体积法求解复杂边界结构时,对流通量与扩散通量会出现扩散现象影响精度[7]。因此也有大量学者采用了有限元法对流场问题求解,而有限元法又由于对控制方程处理离散方法不同,分为伽辽金有限元法、迎风有限元法及最小二乘有限元法。而对于大型求解对流占优问题时,伽辽金有限元法存在数值振荡,所以往往选择最小二乘有限元法与迎风有限元法。刘刚等[8]基于三角形网格采用迎风有限法计算了变压器单分区模型。Liu等[9]运用最小二乘有限元法对变压器流场流动进行了计算。最小二乘有限元法(least-squares finite element method,LSFEM)是在有限元法的基础上,通过最小二乘的思想,将离散方程组的系数矩阵转化为对称正定的稀疏矩阵[10],收敛性较好,且不会出现数值振荡问题。

但最小二乘有限元法在计算流场时,由于高斯积分公式及方程组超定问题,使用四边形网格计算会更加准确。然而对于含有角环、圆形和尖角等复杂部件的电力装备而言,如果仅采用四边形网格剖分,会出现网格形状畸变或者剖分节点畸变,甚至剖分节点无法与边界重合等诸多问题,此时就无法采用最小二乘有限元法进行计算。而三角形网格具有很高的几何灵敏性,对于复杂结构具有良好的贴合性[11]。三角形网格允许在各种形状的单元之间生成高质量网格,例如,在线圈之间的狭窄间隙内,或在本模型范围弧状结构内。此外,它有利于粗四边形和细四边形网格区之间的过渡。张天等[12]用混合网格模拟了复杂结构水下潜器的操作。Alauzet等[13]采用各向异性网格自适应对于叶轮旋转进行了模拟计算。针对复杂结构无法简易剖分问题,目前国内外学者主要的研究方法是使用混合网格或者自适应网格。

针对上述复杂结构二维流场计算的需求,现提出一种三角形网格再处理为四边形的方法,使其适用于最小二乘有限元法。为验证方法有效性,针对方腔顶盖驱动模型,用所提方法的计算结果与Fluent仿真结果进行对比。最后将所提方法应用于具有角环、圆角等复杂结构的换流变压器单分区模型的油流分布计算。

1 无量纲最小二乘有限元法计算油流速度的控制方程

变压器油常常被近似视为不可压缩流体,满足质量守恒与动量守恒定律,稳态情况下的纳维斯托克斯方程可表示为如下形式。

∇U=0

(1)

(ρU·∇)U+∇p=μ∇2U+f

(2)

式中:U为速度,m/s;ρ为流体密度,kg/m3;μ为动力黏度,Pa·s;f为外应力,N;p为压强,Pa;∇为拉普拉斯算子。其中式(2)中等式左边第一项为对流项,第二项为压力梯度项。等式右边第一项为黏性动量,第二项为外应力。

由于式(2)压力-速度耦合方程是速度的二阶偏微分方程,无法直接使用最小二乘有限元法。为此引入涡量ω=∇×U,将上述方程转换为一阶的压力-速度-涡量耦合方程可得

(ρU·∇)U+∇p=μ∇×ω+f

(3)

ω-∇×U=0

(4)

∇·U=0

(5)

对每个变量引入参考量,将各变量与常量无量纲化[14],在直角坐标系中式(3)～式(5)可展开成如下形式。

(6)

将式(6)一阶偏微分方程描述成矩阵方程形式为

(7)

将式(7)中各变量表示成矩阵形式为

(8)

(9)

对矩阵形式的式(7)通过残差公式,以及最小二乘法的基本思想可化为

[A(u+tv]-f)dΩ

(10)

对式(9)进行处理,代入插值函数,便可以得到离散方程组。

其中系数矩阵A为对称正定的稀疏矩阵,最小二乘有限元法的详细推导过程请参考文献[14]。

2 基于三角形网格的LSFEM实现过程

对于图1所示的半圆形仿真模型,在采用四边形网格剖分时,如果采用自由剖分往往会出现网格单元畸变,即出现部分三角形网格的现象,如图1的局部放大图所示。

图1 规则四边形网格畸变为非结构三角形

然而对于大型电力装备而言,由于部件多、形状比图1所示模型复杂得多,在网格剖分时很难实现仅用四边形网格全场域的剖分。此时,如果采用三角形剖分,则具有很好的灵活性,且剖分效果较好,如图2所示。

图2 非结构三角形剖分弧线结构

因此,为了在复杂结构的二维流体场分析中使用无量纲最小二乘有限元法,将通过对三角形网格再处理得到适合最小二乘有限元法使用的四边形网格,过程如下。

步骤1将仿真模型用三角形进行剖分;再对三角形网格单元节点进行再处理得到四边形网格,处理流程如图3所示。

图3 八节点四边形网格形成过程

步骤2在三角形剖分得到图3(a)的网格后,将单元关联矩阵和节点坐标矩阵分别储存。初始三角形含有6个节点,其节点关联矩阵的节点序号如表1所示。

表1 三角形6节点单元节点关联矩阵

步骤3在图3(b)中,先形成一个新节点,即取三角形3个顶点横、纵坐标的平均值作为新节点的坐标,从而形成新的节点关联矩阵和坐标矩阵。

步骤4在图3(c)中,需要将7节点三角形单元形成3个新的四节点四边形单元,即提取原先的一个顶点与相邻的两个边上的节点与四边形中点形成四边形单元,如表2所示。

表2 四边形四节点单元节点关联矩阵

步骤5在将单元编号如表1向表2转化的过程中,需要注意形成单元的节点关联矩阵时,节点序号的编号需按照逆时针顺序排序,否则代入插值函数时计算会出现错误。在图3(d)中,再取每个四边形的每条边的中点,在四边形四节点基础上形成新的节点编号与相应节点坐标,从而得到四边形八节点单元,修改单元信息与节点信息如表3所示,即可完成三角形网格到八节点四边形网格的转变。

表3 八节点四边形单元编号

步骤6在使用所提方法得到四边形八节点网格后,即可以使用无量纲化最小二乘有限元法计算流场速度,其流场的计算流程如图4所示。

图4 基于三角形网格的油流速度计算流程图

3 方法有效性验证

验证模型为如图5所示的顶盖驱动方腔模型,其边长为0.1 m,顶盖水平方向速度为1 m/s,竖直方向速度为0 m/s,剩余三边水平速度与竖直速度均设置为0 m/s,在底边中点设置压力参考点为0 Pa。

u为水平方向速度;v为竖直方向速度;P为压力

对图5模型分别采用四边形和三角形剖分,分别得到1 225个四边形网格和1 210个三角形,再处理成四边形网格,如图6所示。对于三角形网格采用第二部分介绍的方法进行二次处理,然后分别采用有量纲和无量纲最小二乘有限元法对流体场进行计算。有量纲最小二乘法计算时,流体密度为1 000 kg/m3,动力黏度为0.25 Pa·s。无量纲最小二乘有限元计算时,可计算得到雷诺数为400。计算获得的流体场云图如图7所示。

图6 方腔剖分网格

图7 顶盖驱动方腔模型速度云图

从图7速度云图可以看出,基于三角形网格的方法与四边形结果基本一致,仅存在微小差别。为了进一步验证方法的有效性,又取中心线上各点的速度,x=0.05 m,绘制在图8中,同时给出了采用Fluent软件的仿真结果。

图8 中心线速度对比

从图8中可以看出,所提方法有无量纲中心线上的流场速度计算结果与四边形网格的结果基本重合。故只需将本文方法与Fluent中心线水平、竖直方向速度对比,如图9所示。

图9 中心线分向速度对比

经过比较,验证了所提基于三角形网格再处理成四边形网格的方法的适用性。

4 变压器单分区模型油流速度计算

4.1 变压器单分区模型,计算步骤及边界条件

由于网格剖分原因,文献[15]在流-热耦合分析时将静电环和角环等复杂结构假设成“横平竖直”的结构,对计算结果可能带来一定的影响。为此,采用三角形网格对文献[15]中换流变压器模型的单分区模型进行剖分,然后分析其油流分布。

图10为换流变压器绕组的单分区模型。模型大小为108 mm×222 mm,线饼为88 mm×10 mm,油流入口和出口都为10 mm,绝缘筒宽为2 mm,左侧绝缘纸筒长为96 mm,右侧绝缘纸筒长为98 mm,两个绝缘纸筒与油垫圈的连接内侧圆弧半径均为10 mm,外侧圆弧半径均为12 mm。线饼与最下层油垫圈的距离为2 mm,其余每个线饼间的距离为5 mm,线饼与角环的距离也为5 mm,角环厚度为2 mm,角环下侧矩形长为74 mm,角环内侧小圆弧半径为2 mm,角环外侧小圆弧半径为4 mm,角环内侧大圆弧半径为15 mm,角环外侧大圆弧半径为17 mm,角环上侧矩形长48 mm,角环距油垫圈的距离为2 mm,角环上侧的垫圈长为68 mm,最上层的垫圈长为88 mm。由于绝缘筒与油垫圈仅仅只是形状对于油流速度有影响,且暂不考虑其散热影响。因此可以把模型简化成图10右侧的计算模型。

图10 换流变压器局部单分区模型

对图10计算模型采用三角形剖分,网格如图11所示,然后采用所提网格再处理方法进行处理。

图11 换流变压器单分区油流区域网格剖分

采用无量纲最小二乘有限元法计算时,油流入口边界条件设置为u=0.03 m/s,油流出口为压力耦合边界,绕组、角环、油垫圈等固体壁面无滑移边界条件为u=v=0 m/s。变压器油的密度为863.76 kg/m3,动力黏度为0.028 83 Pa·s。

4.2 换流变压器油流速度分布结果

本文方法得到的流体场计算结果如图12(a)所示,为了验证方法的有效性,图12(b)也给出了仿真软件Fluent的云图。

图12 换流变压器单分区内部油流分布云图

由图12可知,本文方法的结果与Fluent结果基本一致,仅在第二油道出口与绕组到角环处存在着微小差距。根据流体力学的知识,可以知道速度在这种情况下不可能突变,所以在第二油道处的速度本文方法计算结果更加准确。油道入口与油道出口附近油流速度相同,满足能量守恒定律。在图12(a)速度云图中,运用本文方法也未出现“死流”现象,验证了本文方法的有效性。

各油道在x=0.054 m处中心点速度如图13所示,可以看出,本文方法数值解基本与Fluent结果变化趋势一致。与Fluent结果相比,本文方法计算的中心点速度在前10个和第12个油道略微偏大,在第11个油道和最后一个油道本文方法油道中心点速度偏小。在最后一个油道中心点速度偏差最大,两者偏差4.6%。

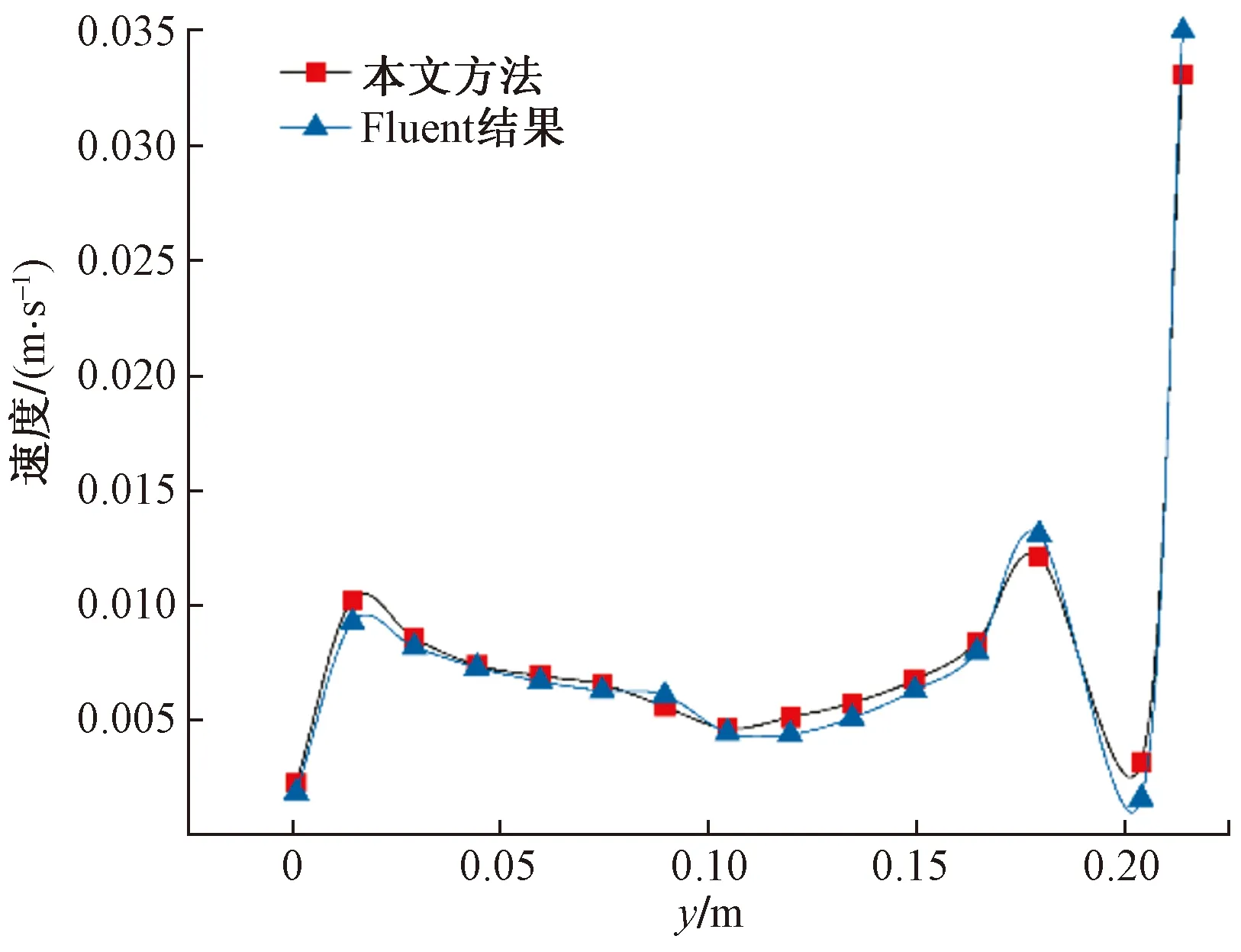
图13 各油道中心点速度分布

进一步提取差距最大的第15油道中心线速度并与Fluent计算结果对比如图14所示。不难发现,两者仅仅只是在速度中心点附近存在微小差距,其他位置速度基本一致。造成这些差距的原因主要有两点,第一是所用方法的不同,Fluent是基于有限体积法,而本文方法是基于最小二乘有限元法,这会造成一定误差。第二是由于二者采用的网格在节点和数量上存在差异,也会造成误差。综上所述,验证了本文方法的有效性。

图14 第15油道中心线速度分布

5 结论

提出了一种基于三角形网格再处理为四边形网格计算二维流体场的方法,并用该方法计算了方腔模型有无量纲速度分布及变压器单分区复杂结构的油流速度分布,与商用软件Fluent结果对比。分析结果表明。

(1)通过方腔模型的对比发现,本文方法在有量纲与无量纲两种情况下计算结果一致,两种方法下均适用。

(2)本文方法能正确计算含角环等复杂部件的变压器模型的油流分布。

本文方法可以对曲面结构具有良好的剖分特性,在计算含复杂部件的电力装备的流场时本文所提方法有良好的适用性。虽然是在三角形网格上进行验证,但是对于含有四边形和三角形的混合网格,本文方法也适用。