异步响应数据对结构模态识别影响的研究

金大帅 （合肥市轨道交通集团有限公司，安徽 合肥 230000）

0 引言

结构健康监测可以有效的对结构的健康状态进行实时监测，出现损伤时能及时预警，将事故伤害降到最低。模态参数是工程结构固有的振动特性，每一阶模态都具有特定的固有频率、阻尼比和模态振型。模态参数识别是结构动力设计及状态评估过程中不可或缺的一环[1-3]。作为一种环境激励下的模态参数识别方法，随机子空间法因具有直接作用于时域数据（data driven）而不必将时域数据转换为相关函数或谱、识别精度高等特点，因此被广泛应用[4-6]。随机子空间法进行结构参数识别时直接作用于实测响应数据，而在模态识别过程中，实测数据的时间不同步可能直接导致识别结果出现偏差。时间不同步直接影响数据之间的相位信息，而相位信息是结构性能和损伤评估的重要指标。为了探究结构异步实测数据对结构模态识别的影响，文章利用ANSYS 有限元仿真软件建立了四层框架结构模型，提取结构不同位置处的异步响应信号，利用随机子空间法识别结构模态参数。

1 随机子空间基本理论

1.1 状态空间方程

式中：xk=x(kΔt)为n维离散的状态向量，n为自由度；yk为N维输出向量，N为响应点数；A 为n×n阶系统矩阵，表示系统的动力特性；B 为离散输入矩阵；C 为N×n阶输出矩阵，描述结构内部状态如何转化为外界的测量值；wk为建模误差或处理过程引起的噪声；vk为传感器误差引起的噪声。

式（1）整理得到随机子空间识别的基本方程：

1.2 模态参数分析

矩阵A的特征值分解如下：

式中：Λ = dia g(λi)，λi为离散时间系统的特征值；ϕ为系统的特征向量矩阵。

由矩阵Λ 得到离散的特征值λi，可用式（4）求得系统特征值ui：

第i阶模态的振型表示为φi= Cϕi。

1.3 随机子空间算法

为计算系统矩阵A 和输出矩阵C，笔者将结构所有测点的响应数据组成2li×j的Hankel矩阵：

式中：hi为第i时刻所有测点的响应数据；Hpast为li×j阶“过去”输出矩阵；Hfuture为li×j阶“将来”输出矩阵。

对Hankel矩阵QR进行分解[9-11]，可将数据从2li×j缩减至li×j，极大地减少数据量，加快程序的运行。QR分解可表示为：

将Hankel 矩阵中的“将来”输出矩阵向“过去”输出矩阵的行空间进行正交投影，得到投影矩阵Oi。投影矩阵可表示为：

对投影矩阵SVD进行分解：

另外，还有个重要定理：

式中：Γi为可观测矩阵；为卡尔曼滤波状态向量矩阵。

则由式（7）、式（8）可得：

采用最小二乘法可得：

其中：·†表示矩阵·的广义逆矩阵。

SVD 分解后，矩阵S1的秩可以确定系统的阶次。至此，即可识别出系统矩阵和输出矩阵。

2 结构仿真模型与模态识别

用ANSYS 软件进行建模，在框架结构右侧设置4 个间距相同的信号采集点，对框架左侧施加激励。框架结构具体参数为宽度a=6 m、四层框结构每层高h=2.9 m、柱子采用beam188 单元、横梁采用shell63 单元。材料属性参数为，柱子为矩形截面、弹性模量E=25 GPa、泊松比为0.2。横梁为矩形截面，弹性模量E=30 GPa。在框架右侧等距离设置四个信号采集点，如图1所示。

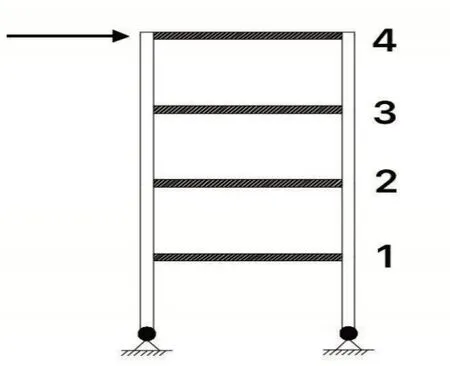
图1 框架结构测点布置图

采用ANSYS 软件建模完成后，对框架进行模态分析，计算得到前三阶自振频率和振型如图2所示。

图2 框架前三阶模态振型图

框架模态分析结束后，对框架结构施加零均值的噪声作为结构的激励。利用ANSYS 有限元分析软件中的瞬态分析，提取各测点加速度响应数据，最后设置相应工况对结构响应信号进行异步采样。对框架结构指定位置施加噪声激励后，结构不同测点的响应数据采集进行如下处理。首先1 号测点开始采样，同时其他测点未开始采集数据；2 号测点在1 号测点采样1 s 后开始采样；3 号测点在1 号测点采样2 s 后开始采样；4 号测点在1 号测点采样3 s 后开始采样，采样频率均为400 Hz，加速度响应采集结束后，利用随机子空间方法对异步采样数据进行模态参数识别。

首先设置稳定图满足的计算参数，取值分别为自振频率的稳定标准取值0.5%，阻尼比的稳定标准取值2%，模态振型的稳定标准取值0.5%。利用稳定图程序对采集的异步响应数据进行计算，得到的稳定图如图3所示。

图3 框架结构稳定图

通过选取图3 中前三阶稳定轴的稳定点可以确定结构的模型阶次，确定模型阶次后识别得到结构频率和结构振型。简支梁的异步响应数据模态频率计算结果如表1所示。

为了更好反映计算振型与识别振型的相关性，引入振型相似因子的概念，定义振型相似因子DMAC如下[12]：

DMAC=1-MAC

一般情况下DMAC 值偏向0 时，认为两个振型是同一振型；反之，偏向1 时认为是不同振型。根据研究所得，当DMAC＜0.05 时，可认为两振型为同一振型[13-14]。

在得到前三阶频率识别结果后，将识别的前三阶结构振型和ANSYS有限元计算振型进行归一化对比，得到振型图和相应的振型相似因子如图4所示。

图4 框架模拟异步振型识别

通过识别结果可知，一阶频率识别差值为0.008 Hz、二阶频率识别差值为0.125 Hz、三阶频率识别差值为0.706 Hz，前三阶自振频率的振型相似因子均满足DMAC＞0.05。通过识别结果可知，随机子空间法对异步实测数据的振型识别效果较差，前三阶振型相似因子DMAC均不满足同一振型的判定条件。

3 结论

使用随机子空间法识别桥梁模态参数时，通常直接对测点的实测响应数据进行处理。理想情况下信号采样点之间进行同步采样，利用模态识别方法，可以通过同步采样信号，较好的识别出结构的模态参数。当结构测点的采样时间不同步时，会对结构的模态参数（特别是模态振型）产生显著的影响。在异步采样的影响下，由于模态振型的识别结果不能满足与理论振型是同一个振型的定义，因此在实际工程应用中，应当细致考虑结构的异步响应数据对结构模态振型识别的影响。