卷积视角下循环矩阵对角化证明新方法及其应用

唐毅鋆,陈颖频,陈 惠,乔嘉琪,陈振雕,李一凡

(1.漳州职业技术学院电子信息学院,福建 漳州 363000;2.闽南师范大学物理与信息工程学院,福建 漳州 363000)

0 引言

在图像处理和计算机视觉的众多应用中广泛存在具有列循环结构或行循环结构的循环矩阵,例如图像处理中的差分矩阵[1-2]和相关跟踪滤波中由基向量循环移位得到的预测样本矩阵[3-8]。由于循环矩阵在空间上存在明显的循环移位关系,其信息存在冗余性,因此若直接在空域上处理循环结构矩阵会导致产生较高的计算复杂度。为解决这一问题,学者们将傅里叶变换引入循环矩阵,并将大型的矩阵相乘和求逆运算转换为向量的点乘与点除运算,其核心原理就是循环矩阵的对角化性质。然而,传统的循环矩阵对角化性质的证明较难理解和掌握,为此,本文从卷积视角提出一种全新的列循环矩阵对角化证明方法,进而证明行循环矩阵的对角化性质。

1 预备知识

1.1 传统的列循环矩阵对角化证明方法

循环矩阵对角化问题描述如下:

(1)

根据复数信号的周期不变性,

ekj2π/N=ekj2π/N·e-2πkj=e-kj2π(N-1)/N.

(2)

同理,

ekj2π(N-1)/N=ekj2π(N-1)/N·e-2πkj=e-kj2π/N.

(3)

因此,

(4)

g(1,k)=x1+x0ekj(N-1)2π/N+…+x2ekj2π/N=ejk2π/Ng(0,k).

(5)

则

(6)

故有

(7)

1.2 离散信号卷积定义

z=x*y∈N×1,

(8)

1.3 列循环矩阵的一个性质

将列循环矩阵C(x)乘以一个信号y,根据1.2节中介绍的离散卷积定义,则有

(9)

2 卷积视角下列循环矩阵对角化证明

2.1 列循环矩阵对角化性质证明

根据式(9),在两边乘以离散傅里叶变换矩阵FN,则有

FNC(x)y=FN(x*y).

(10)

首先分析式(10)右边,根据卷积定理,空域卷积信号的频谱将等于两个信号频谱的点乘[10-11],即

(11)

然后分析式(10)左边,将C(x)y看作C(x)INy,其中,IN∈N×N表示单位矩阵,可被拆分为则有

(12)

由于式(10)成立,必有

(13)

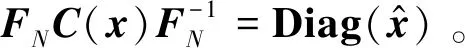
2.2 列循环矩阵对角化性质验证

本节提供代码1对列循环矩阵对角化性质加以验证,代码如下:

%代码1

clear all;

N=4;

DFT=zeros(N,N);

n=[0:N-1]; k=[0:N-1];

Wn=exp(-j*2*pi/N);

nk=n’*k;

DFT=Wn.^nk;

C=[-1 1 0 0; 0 -1 1 0; 0 0 -1 1; 1 0 0 -1];

x=[-1,0,0,1].’;

X=fft(x);

D=DFT*C*inv(DFT);

for i=1∶N

Y(i)=D(i,i);

end

Y-X.’

经Matlab运行,代码1运行结果约等于0。该结果表明,运用卷积定理进行列循环矩阵对角化与通过传统数学方法计算的误差极小,可见式(7)成立。

3 行循环矩阵对角化性质证明

3.1 利用列循环矩阵对角化性质证明行循环矩阵对角化性质

证明 因(7)式恒成立,对该式两边同时转置,则有

(14)

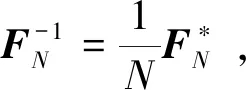
(15)

(16)

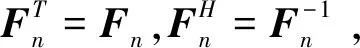
(17)

3.2 行循环矩阵对角化性质的编程验证

本节提供代码2对行循环矩阵对角化性质加以验证,代码如下:

%代码2

N=8;

DFT=zeros(N,N);

n=[0∶N-1];

k=[0∶N-1];

Wn=exp(-j*2*pi/N);

nk=n’*k;

DFT=Wn.^nk;

Fn=DFT./sqrt(N);

C=[0 7 6 5 4 3 2 1;

1 0 7 6 5 4 3 2;

2 1 0 7 6 5 4 3;

3 2 1 0 7 6 5 4;

4 3 2 1 0 7 6 5;

5 4 3 2 1 0 7 6;

6 5 4 3 2 1 0 7;

7 6 5 4 3 2 1 0];

D=inv(Fn)*C*(Fn);

for i=1∶N

y(i)=D(i,i);

end

x=[0 7 6 5 4 3 2 1];

FTx=fft(x);

y-FTx

以上代码中,C以(0, 7, 6, 5, 4, 3, 2, 1)作为第一行,经循环移位扩展得到行循环结构矩阵。代码2运行结果趋近于0,该结果表明,运用卷积定理进行行循环矩阵对角化与通过传统数学方法计算的误差极小,可验证式(17)成立。

3.3 行循环矩阵在视频目标跟踪中的应用

在相关滤波跟踪算法中,常将二维目标面片X∈h×w拉成行向量xT∈1×N(N=h×w),并循环移位扩展为行循环矩阵,以此建模目标在空间中移动的各种可能性,如图1所示。

(a)循环移位得到的预测样本1

(b) 基样本

(c)循环移位得到的预测样本2

然后以岭回归的机器学习建模方法训练滤波器w∈N×1,使得滤波器回归的响应尽可能接近预先定义的教师信号N×1(该信号为二维高斯窗函数的拉列信号),如式(18)所示。

(18)

目标函数在空域上对滤波器w进行求导:

(19)

则w的空域最优解为

(20)

若样本尺寸较大,在空域上直接求解滤波器w的复杂度很高。行循环矩阵的对角化性质则可较好地解决这一问题。

将式(20)中的C(xT)对角化:

根据卷积定理可将式(21)转换到频域中计算,则有

(22)

其中,real表示取复数的实部。

图2展示了利用式(20)和(22)设计滤波器得到的响应图,从图2可以看出,两种算法效果上完全等效。通过上述方法可将滤波器利用快速傅里叶变换加以计算,运算效率会有显著提高。

(a)利用式(20)设计滤波器得到的响应图

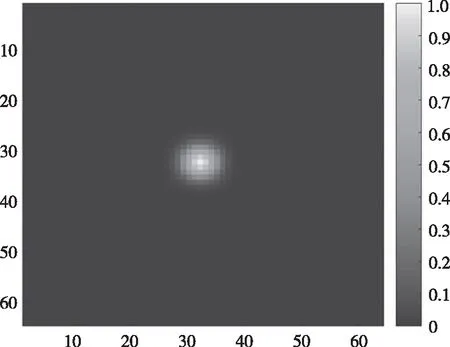
(b)利用式(22)设计滤波器得到的响应图

本节提供代码3以反映式(20)与(22)计算效率上的差别。代码如下:

%代码3

clc

clear all;

N=4096;

X1=[1∶1∶sqrt(N)];

X2=[1∶1∶sqrt(N)];

[X,Y]=meshgrid(X1,X2);

y=exp(-((X-sqrt(N)/2).*(X-sqrt(N)/2)+(Y-sqrt(N)/2).*(Y-sqrt(N)/2))/10);

C=zeros(N,N);

x=linspace(1,N,N);

C(1,:)=x.’;

for i=1∶N-1

C(i+1,:)=circshift(x,i).’;

end

tic

w=inv(C.’*C+0.1)*C.’*y(:);

toc

r1=C*w;

figure(1)

R1=reshape(r1,sqrt(N),sqrt(N));

imagesc(R1);

colorbar;

tic

w2=real(ifft(fft(x.’).*fft(y(:))./(fft(x.’).*conj(fft(x.’))+0.1)));

toc

r2=C*w2;

figure(2)

R2=reshape(r2,sqrt(N),sqrt(N));

imagesc(R2);

colorbar;

r1-r2

通过改变代码3中N的数值,对比两种算法的运行时间,如表1所示。

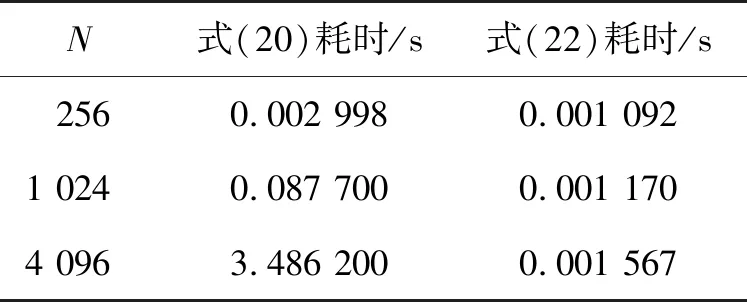
表1 式(20)与式(22)的耗时对比

从表1可以看出,当N值较大时,以式(22)计算滤波器的运算耗时远远低于以式(20)计算滤波器的运算耗时。这是因为式(20)涉及大型矩阵C(xT)∈N×N的相乘运算和求逆运算,其复杂度高达(N3),而式(22)中用到的快速傅里叶变换和快速逆傅里叶变换复杂度仅为(Nlog2N),且向量的点乘运算复杂度仅为(N2),故式(22)复杂度为(N2+2Nlog2N)。因此,利用循环矩阵对角化将滤波器转换为频域求解的效率较高。

4 结语

循环矩阵对角化性质广泛应用于各类图像处理和计算机视觉领域。然而,传统的循环矩阵对角化证明方法往往晦涩难懂,需要用到大量数学技巧。为解决这一问题,本文从列循环矩阵的性质C(x)y=x*y出发,结合离散卷积定义和卷积定理,从卷积视角巧妙证明了列循环矩阵的对角化性质,避免传统证明方法中涉及的复杂运算,证明思路易于理解,最后通过行循环矩阵与列循环矩阵的转置关系进一步讨论行循环矩阵的对角化性质,并给出一组实验以反映行循环矩阵对角化性质在视频目标跟踪中的重要应用。