生产场景下回焊炉核心温度数值计算方法

朱调娟

(惠州经济职业技术学院信息工程学院,广东 惠州 516057)

0 引言

由于电路板厚度相比于电路板长度和宽度相差较大,电路板的加热过程主要是上下表面到中心的传热过程.如果以电路板作为参照系,电路板在回焊炉中运动加热的过程可简化为电路板上下表面温度随时间变化的一维传热过程[1-2].在加热过程中箱体内空气与电路板表面对流换热、电路板内热传导、加热器件与电路板之间热辐射三种热量传递方式都有发生,是一个复杂的过程(图1).

图1 加热过程中各种热量传递方式示意图

可靠的传热方程是进行控制优化的基础,然而方程中诸如热传导系数、比热、辐射吸收强度等在不同的生产条件下都不尽相同,如果依赖于实验测定,一方面增加了系统的复杂度,另一方面不能与生产实际灵活匹配[3-4].简便可行的方式是利用在电路板中心部署的测温传感器获得的数据,拟合出一组适用于当前生产条件的参数.

加热及风冷装置上下对称布置,因此可以认为电路板沿纵向的温度分布具有对称性,取电路板厚度方向上的中心剖面作为绝热面建立热能传递方程[5-7].热辐射和对流热量都是从表面进入电路板的,适合采用第三类边界条件:

(1)

1 建立差分方程

核心温度的时间导数采用向前差商.对于二阶导数项,考虑到只有核心的温度数据,缺少沿着板厚方向的数据,因此不便插入其他分层,只能依赖边界热流做向前差商.

(2)

(3)

如果直接采用这样的离散方式是难以进行良好的拟合和估计的.

联立边界的向后差商和热流边界条件:

还可以推出,边界温度是热源和核心温度之间的一种线性组合.

其中的组合系数只依赖于表面传热系数b和板的厚度h,显然这样的常系数对边界温度复杂的非线性变化的描述不够.采取在前后两时间步使用不同组合系数的方式,增加在数值计算和拟合时非线性的程度.修正后的边界温度表示为

(4)

该时间步传热开始时边界温度表示为热源和核心温度线性组合的组合系数β,传热结束时组合系数变为α,从而在每一个时间步内边界温度的变化是非线性的,这两个系数仅在每个单独的时间步上有效,将α和β分别代入(2)式.

(5)

由于沿厚度方向缺少划分点,依赖边界条件得出的离散公式实际上很难直接用于拟合和估计.而沿时间方向有丰富的分点及测量数据,因此要想提高计算精度和计算稳定性,需要充分利用时间维度上的离散化.

(6)

将温度对时间导数的泰勒公式作为出发点,将温度对时间的二阶导数项采用向前差商进行离散,并利用热传导方程将时间的一阶导数转化为对空间的二阶导数.

再利用(4)式可得到

(7)

将(6)式代入(5)式,对其中的一阶导数项采用向后差商进行离散,整理可得到

u(0,ti+1)-u(0,ti)=(1-τA)(u(0,ti)-u(0,ti-1))+τAf(vti)-τBf(vti-1)+τCu(0,ti-1)+o(τρ).

由此得出回归基本方程:

(8)

以及温度演化关系:

(9)

2 拟合生产场景参数

回焊炉内的炉温为一分段函数f(z),在第i个温区[l2i-1,l2i]内温度为Ti,在相邻温区间隔[l2i,l2i+1]上温度为线性变化.

(10)

对核心温度测量数据与f(z)在采样点的取值,按(7)式进行多元线性回归.

在图2中,u为核心温度的一系列采样点,u*为按照拟合系数进行差分计算得到的核心温度仿真结果,

f为炉温函数.

将得到的系数按照(8)式进行仿真模拟,由图2可以看出,仿真模拟数据与实际测得的核心温度之间有明显的偏差.实际上这是因为在不同炉温下辐射换热强度不同,并且在回焊炉尾段其换热的主要方式变为采取强对流的方式散热,这些在热传递方程中都归结为表面传热系数.因此在不同工况下的热传导系数a和表面传热系数b应取不同的值,进而采取分段回归及仿真方式,按炉温函数的分段设定为5个对应阶段,分别计算回归系数并进行仿真,分段回归系数见表1,仿真结果如图3所示.仿真结果所反映出的温度变化与实测核心温度曲线吻合得很好.在图4中,res表示分段拟合后按照差分计算仿真得到的残差,res始终保持在-1.5℃～+1.5℃范围内,说明采用(8)式进行数值计算时的累积误差不明显.

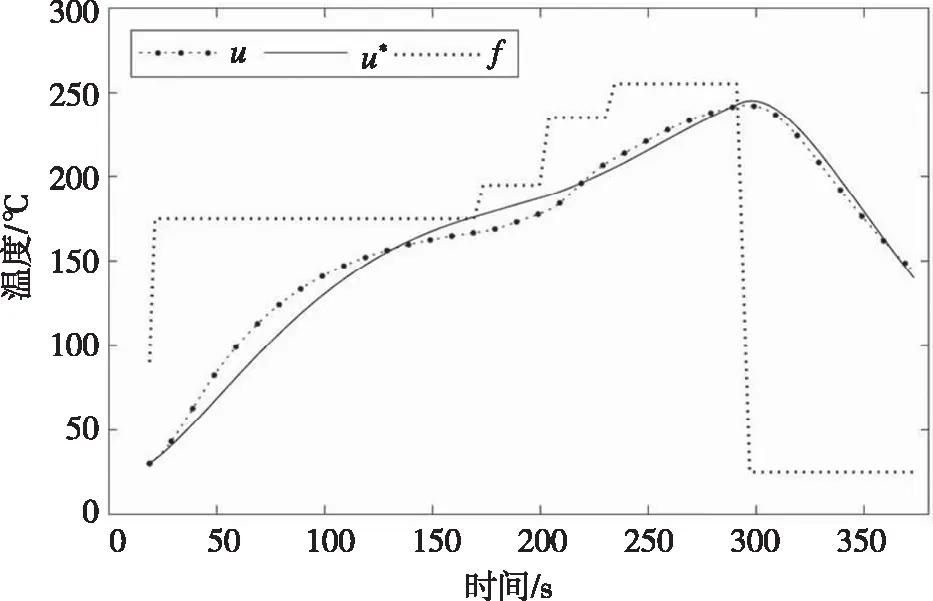
图2 整体拟合时得到的温度曲线

图3 分段拟合时的仿真结果与采样点测量值之间的关系

表1 分段回归系数

图4 仿真结果和实测值之间的残差图

图5 修正后的仿真残差正态概率图

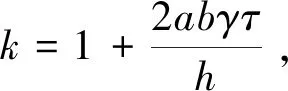
Δu(0,ti+1)=kΔu(0,ti)+o(τh)+o(τ2).

(11)

3 进一步修正

从图4所示的残差res曲线可以看出,当前仿真结果仍存在一定的系统误差,这是因为在计算时将炉温函数处理成了简单的分段函数,尤其是在温区间隔上假定为线性变化,这在大范围恒温和温差较大的地方产生明显的误差.考虑对炉温函数进行修正,仍采用分段线性函数,但是通过扩大相邻温区间隔这种最简单的方式来强化温区间的相互影响,修正后重新拟合误差降至-0.5℃～+0.5℃范围内,残差曲线如图4中的res_fix曲线所示.残差正态概率如图5所示,在图5中绝大多数点在一条直线上,偏离较大的地方主要是冷却段炉温变化较大的地方,这些地方除了炉温函数用分段线性可能不足以描述其变化的非线性性,还受到累积误差的影响,这类模型计算时的累计误差基本无法避免,从误差的范围来看,采用(9)式计算的累积误差控制效果较好.

4 结语

拟合及仿真计算结果表明,本文建立的回归方程(8)和相应的差分方法(9),既有理论依据,又与实际观测数据有良好的吻合,不需要更多的外部数据和其他假设,是一种可靠的仅利用核心温度观测数据就可以对回焊炉加热过程进行估计和仿真的方法,可以进一步对加热过程进行控制和优化.