两种概念生成算法的比较分析与实验仿真
吴清寿,何清恒,刘书阳
(1.武夷学院数学与计算机学院,福建 武夷山 354300;2.福建省茶产业大数据应用与智能化重点实验室,福建 武夷山 354300)
0 引言
形式概念分析(Formal Concept Analysis,FCA)[1]已广泛应用于各种数据分析任务,如文本挖掘[2]、复杂网络分析[3]等。关于FCA的研究中,概念生成及概念间关系构建是各项研究工作的基础,得到研究人员的长期关注[4-5]。从形式背景中生成概念,研究人员已提出了很多算法,主要包括批处理[5-6]和增量式[7-8]两类不同的处理方法,增量式构建概念格方法主要研究节点间关系的快速查找,批处理的方法则侧重于从背景中快速生成所有的概念内涵或外延。不管是哪一类概念生成算法,其首要任务是保证算法的正确性,即能对一个形式背景生成全部的概念,另一个重要任务就是提出合适的规则,以期加快概念生成的速度和概念格中概念关系的构建。
批处理方法中,GANTER[6]提出的NextClosure算法是一种基于闭包运算的方法,从最小外延(一个闭包)开始,基于字典序找到大于当前闭包的最小闭包,即另一个外延,直到找到最大的闭包(所有属性的集合)为止。NextClosure算法具有较好的时间性能,得到了研究人员的关注,如孙斌斌[9]在NextClosure算法的基础上提出Tri-NextClosure算法,用于对三维数据进行数据分析,林志鸿等[10]对NextClousea算法在实现方面存在的问题进行了讨论并提出改进措施。另一种基于基本定义和基本原理导出的概念生成算法[11]也具有一定的代表性,其主要原理是:若X∈M,则(g(X),f(g(X)))一定是概念,其中M是形式背景的属性集合。庞智恒等[12]运用与上述方法相似的原理,逐层生成概念,同时构建了格节点间的偏序关系。吴清寿等[5]将每个属性导出的概念进行划分,减少了无效的搜索次数,使算法具有较高的运行效率。
以上两种经典算法常用于作为新提出算法的对比算法或改进依据,但在相关文献中没有得到深入全面的分析。本文拟对两种算法进行较为全面的分析,阐明基本原理,给出算法步骤,并结合实例分析算法的优缺点,最后进行实验仿真,为后续的概念生成算法研究提供可靠的理论依据。
1 基本理论
定义1[11]设U是对象的集合,M是属性的集合,R是集合U和M之间的关系,则三元组K=(U,M,R)是一个形式背景(简称背景)。对于u∈U,m∈M,(u,m)∈R表示对象u具有属性m。通常,用矩阵表示背景,其中,每一行表示一个对象,每一列表示一个属性。
一个背景的例子如表1所示。第一列是对象集合,第一行是属性集合,行列交叉处的“×”表示该行对象具有该列对应的属性,如第三行,对象3具有属性a、b、d和f,将这种对应关系记为二元组({3},{a,b,d,f})。

表1 形式背景示例
定义2[11]对于背景K=(U,M,R),若X⊆U,Y⊆M,令f(X)={m∈M|∀u∈X, (u,m)∈R},g(Y)={u∈U|∀m∈Y,(u,m)∈R}。若X,Y满足f(X)=Y,g(Y)=X,则二元组(X,Y)是一个形式概念(简称概念),记为c,其中X为概念c的外延,Y为概念c的内涵。
如有X={2,5},则f(X)表示对象2和对象5共同具有的属性集合,由表1可知,f(X)={a,e}。若有Y={a,e},则g(Y)表示具有属性a和e的对象集合,所以g(Y)={2,5,6},这里f(X)≠g(Y),则二元组({2,5},{a,e})不是概念。若X={2,5,6},Y=({a,e},f(X)=g(Y),则二元组({2,5,6},{a,e})是一个概念,{2,5,6}是外延,{a,e}是内涵。
2 基于基本定义的概念生成算法
定理1[11]对于背景K=(U,M,R),若P∈U,则(g(f(P)),f(P))一定是概念;若Q∈M,则(g(Q),f(g(Q)))也一定是概念。
如有P={1},f(P)={a,f},g(f(P))={1,3},则({1,3},{a,f})一定是一个概念。
根据定理1,只要找到所有的内涵或所有的外延,则可找到所有的概念。要找到所有的外延,只需对M的所有子集进行穷举即可,进而生成所有概念。然而,对M的子集进行穷举的时间复杂度是O(2n),其中,n是属性数量。显然,穷举法在属性数量较大的情况下是难以实现的。为了找到全部未出现的外延,对于每一个可能的外延都需要判断其是否已经出现在已求得的外延集合中,需要设计一种合理的方法。因此,从概念的定义出发,设计以下步骤:设置一个初始概念(U,∅),将初始概念加入概念表C中,将U加入外延表E中。对于∀m∈M,首先计算g(m),再逐一计算s=g(m)∩ei,其中ei∈E。若s∉E,则s是一个外延,将s加入E中,计算f(s),将(s,f(s))加入概念表C中。重复以上过程,直到所有属性m都处理完毕。为方便叙述,将以上算法简记为CGA(Concept Generation Algorithm)。
2.1 算法描述
具体的计算过程如算法1所示。
算法1:CGA
输入:背景K=(U,M,R)
输出:所有概念集合C
1C←{(U,∅)}
2E←{U}
3 for eachm∈Mdo:
4T←E
5 for eache∈Edo:
6s←g(m)∩e
7 ifs∉Tthen:
8T←T∪s
9C←C∪(s,f(s))
10 endif
11 endfor
12E←T
13 endfor
14 returnC
算法1中,遍历E时,E是由当前属性前面的其他属性所生成的外延集合,但在判断s∈E时,需要对由当前属性生成的外延也进行判断,所以用T保存E中的外延,并在有新的外延生成时将其加入T中,当前属性处理完毕后,再将T中的外延更新到E中,作为下一个属性的前置外延。
2.2 实例分析
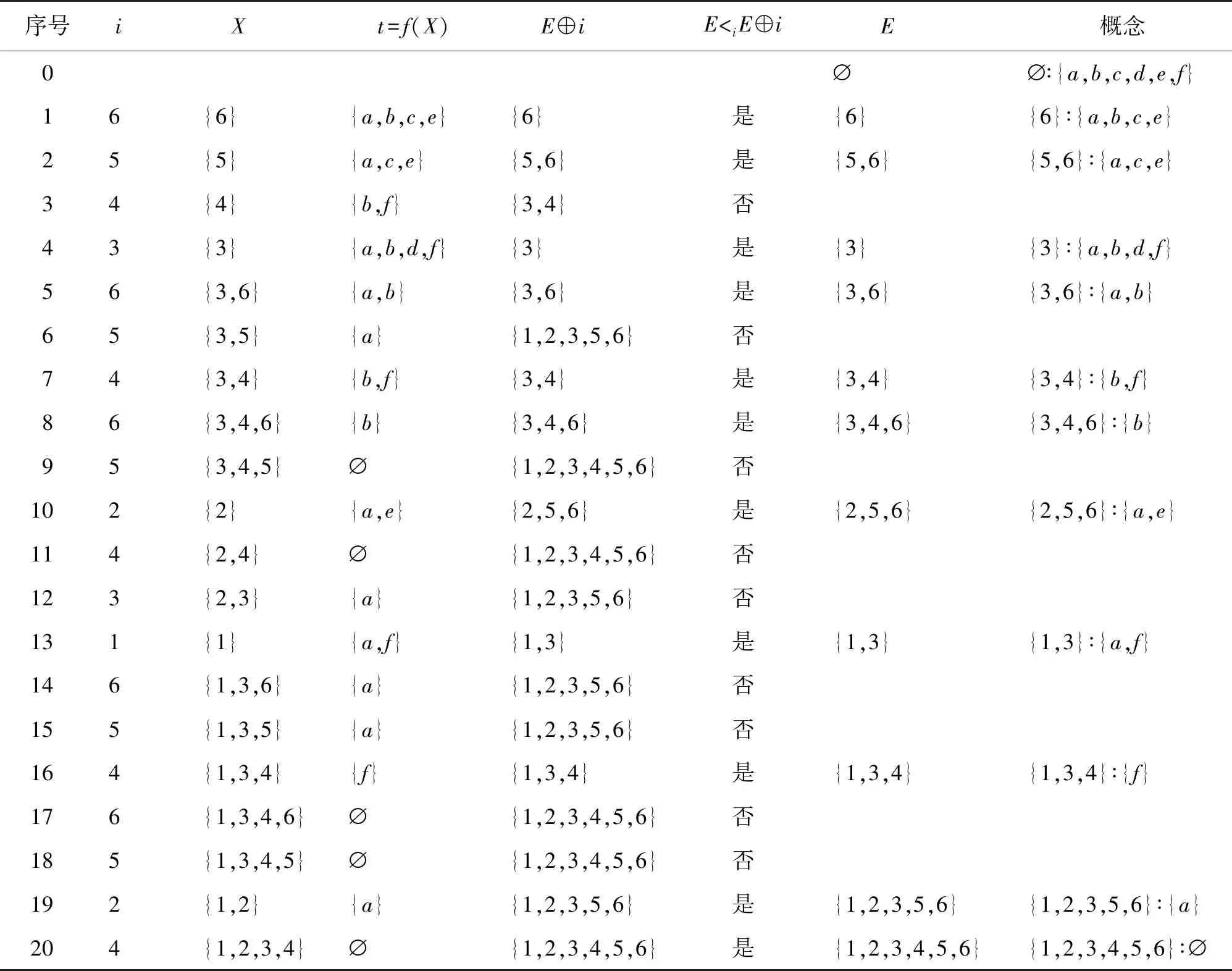
根据算法1,首先设置两个集合C和E,分别用于存放已生成的概念和外延,再根据算法逐步查找外延,从表1的背景生成全部概念的过程如表2所示。

表2 CGA算法生成全部概念
以从属性e生成概念的计算过程为例进行说明。在对属性e进行处理之前,外延表E中已有8个外延,同时将E中外延保存到T中。首先计算g(e)={2,5,6},再计算s=g(e)∩e1={2,5,6},因为s∉T,将s加入T中,此时T中的外延集合为{{1,2,3,4,5,6},{1,2,3,5,6},{3,4,6},{3,6},{5,6},{6},{3},∅,{2,5,6}}。然后,g(e)与e2~e8进行交运算得到的{2,5,6}、{6}、{5,6}和∅都已在T中,没有产生新的外延。至此,由属性e生成概念的操作结束,进行下一个属性的操作。
3 Nextclosure算法
3.1 算法理论
定义3[11]对于背景K=(U,M,R),有X,Y⊆U,X和Y中的元素按升序排序。对X和Y中的元素从第1个元素开始比较,若首次出现不相等元素的位置为i,且Xi>Yi,则称X字典序地小于Y。这里规定∅的字典序最小。
定义4[11]对于X,Y⊆U,i∈U,将X 定理2[11]对于X⊆O,字典序地大于X的最小外延是X⨁i,i是满足X 根据以上原理,Nextclosure算法的主要步骤如下:首先设一个最小外延E=∅及最小概念(∅,U),根据E 算法2:NextClousure 输入:背景K=(U,M,R) 输出:所有概念集合C 1C←{(∅,U)} 2E←∅ 3U’←sort(U,DESC) 4 whileE≠Udo: 5I←U’-E 6 for eachi∈Ido: 酒精性肝病的治疗方面,马萨诸塞大学医学院Szabo(摘要LB-1)一项多中心随机双盲安慰剂对照的临床试验报道了IL-1受体激动剂联合己酮可可碱和锌治疗重症酒精性肝炎28 d,终点指标为30 d、90 d及180 d的病死率,与甲泼尼龙(32 mg每日口服,28 d)比较,短期疗效相近,长期疗效新的治疗更有优势。 7X←E∩{1,…,i-1}∪{i} 8T←f(X) 9F←g(T) 10 ifE∩{1,…,i-1}=F∩{1,…,i-1} then: 11E←F 12C←C∪(F,T) 13 break 14 endif 16 endwhile 17 returnC 根据算法2,首先设置一个最小概念(∅∶{a,b,c,d,e,f}),再根据S 表3 NextClosure算法生成全部概念 下面以从概念({2,5,6}∶{a,e})产生下一个概念的计算过程为例进行说明。 当生成概念({2,5,6}∶{a,e})后,开始生成下一个概念。首先需要确定i的取值范围,根据定义4,i∈U-E={1,2,3,4,5,6}- {2,5,6}={4,3,1},所以从i=4开始。 当i=4时,首先求E⨁i。令X=E∩ {1,…,i-1}∪{i}={2,5,6}∩{1,2,3}∪{4}={2,4},f(X)=∅, E⨁i=g(f(X))={1,2,3,4,5,6}。再判断E 当i=3时,首先求E⨁i。令X=E∩ {1,…,i-1}∪{i}={2,5,6}∩ {1,2}∪{3}={2,3},f(X)={a},E⨁i=g(f(X))= {1,2,3,5,6}。再判断E E⨁i∩{1,…,i-1}= {1,2,3,5,6}∩{1,2}={1,2},E⨁i∩{1,…,i-1}≠E∩{1,…,i-1},即E 当i=1时,首先求E⨁i。令X=E∩{1,…,i-1}∪ {i}={2,5,6}∩∅∪{1}={1},f(X)={a,f},E⨁i=g(f(X))= {1,3}。再判断E 通过对以上两个算法在同一背景上生成概念过程进行分析,可知两个算法在方法和步骤上都存在较大的差异,这些差异对算法的运行效率有较大的影响。下面对两个算法的区别进行讨论。 CGA算法中,每一趟判断需要的集合操作有:计算g(m),因为m是单个属性,求解g(m)的时间基本可以忽略。求解s需要一次交集运算g(m)∩ei,若s不是外延,则无需计算f(s),否则需要计算f(s),这里计算f(s)的次数与概念数量相同。由上述算法步骤及实例分析过程可知,CGA算法思想简单,易于实现。但该算法也存在以下问题:(1)CGA算法的运行效率与属性数量紧密相关,每增加一个属性,就需要多一轮概念生成的求解过程,需要将新的属性对应的对象集合与已生成的全部概念外延进行逐一比较,越处在表格后端的属性,需要比对的次数就越多;(2)在生成概念的过程中存在较多的冗余计算,如对于属性e的计算中,只生成1个概念,而其余的7次计算产生的结果都是与已有外延重复的。 Nextclosure算法存在的一个问题是在生成下一个概念的过程中,可能需要多次改变i值才能找到满足条件的外延,即对于对象数量多的背景,其运行效率可能较差。另外,Nextclosure算法的一趟求解需要大量的集合操作,从当前概念出发,首先需要进行一次差集运算U’-E,求解X需要一次交集运算E∩ {1,…,i-1},然后进行f(X)(记为T)和g(T)操作,最后判断E 为了验证两种算法的时间性能,下面对两种算法进行实验仿真。实验环境:Intel Core i7-8650U CPU,16 G RAM,Windows10操作系统。算法均采用Python语言实现。 实验数据集采用人工生成的形式背景,生成背景的主要参数包括:对象数量|U|、属性数量|M|和每个对象的平均属性填充率f。 为了让人工生成的背景更加接近真实场景,每行填充的属性数量按高斯分布生成,填充数量的均值μ=|M|×f,标准差δ=μ/2,最小值为1。两组数据集的参数设定如下: Bg1:|U|=500~2 500,|M|=50,f=0.1; Bg2:|U|=50,|M|=500~2 500,f=0.1; 以上两组数据集的参数设置主要考虑以下实验场景:Bg1用于测试算法对|U|增长下的适应性,Bg2用于测试算法对|M|变化的适应性。其中,Bg2是对Bg1中背景的转置,两者生成的概念数量一致,但每个概念中的内涵和外延是调换位置的。 通过实验对以下三个方面进行比较:一是生成的概念数量;二是生成概念过程中的总迭代次数;三是在不同背景上的运行时间。 首先,两种算法在两个背景上生成的数量是一致的。因为两个背景中包含的概念数量相同,这里只列出在Bg1上的概念数量,结果如表4所示。 表4 两个算法在Bg1上得到的概念数量 表4中,概念的数量总体上是随着|U|的增大而增加的,在|U|值为700和800时概念数量有所下降,主要是由背景中属性填充的随机性导致的。 其次,对两个算法中求解外延的迭代次数进行比较,具体地,在CGA算法中对s=g(m)∩ei的计算次数进行统计,在NextClosure算法中对每个E 表5 两个算法在Bg1上的迭代次数 表6 两个算法在Bg2上的迭代次数 表5为两种算法在Bg1上的实验结果,其中|M|很小,而|U|不断增大,所以CGA算法的计算次数少,而NextClosure算法的计算次数多,且随着|U|的增大,NextClosure算法的计算次数快速增加。表6中呈现的实验结果刚好与表5相反,这是因为背景转置后,Bg2中|U|很小,而|M|不断增大引起的。可见,CGA算法和NextClosure算法两者适应的背景是不一样的。 最后,对两个算法的运行时间进行对比,如图1和图2所示。在Bg1上,CGA算法对所有的背景都在1 s内完成计算,而NextClosure算法需要大量的计算时间;在Bg2上,两种算法的运行时间较为接近,但CGA算法仍然比NextClosure算法具有时间性能上的优势。 图1 两个算法在Bg1上的运行时间 图2 两个算法在Bg2上的运行时间 以上实验结果表明,CGA算法在时间性能上优于NextClosure算法,尤其是在对象数量多而属性数量少的背景上,CGA算法的优势更加明显。两种算法的运行时间都随着寻找概念外延的次数增加而相应增加,但影响算法时间性能的最主要因素是寻找一个外延所需的集合运算次数。由表6可见,在同一背景上(如|M|=1 000),CGA算法运算次数是NextClosure算法运算次数的40倍,但CGA算法总体运行时间仍少于NextClosure算法总体运行时间,主要原因是CGA算法中集合操作次数少,大大节省了一次查找外延的时间,所以CGA算法总体上有更好的时间优势。 本文介绍了两种经典的概念生成算法,从算法原理、算法步骤和实例等方面进行了对比分析,并用Python语言实现了两种算法,在两类数据集上进行了实验仿真。结果表明,要提高概念生成算法的运行效率,首要任务是减少概念外延生成过程中的交集运算,然后进一步寻找规律,减少无用运算次数。下一步的工作中,进一步提高概念生成效率将是我们研究的重点。3.2 算法描述
3.3 实例分析
4 两种算法的对比分析
5 实验仿真
5.1 实验环境与数据集
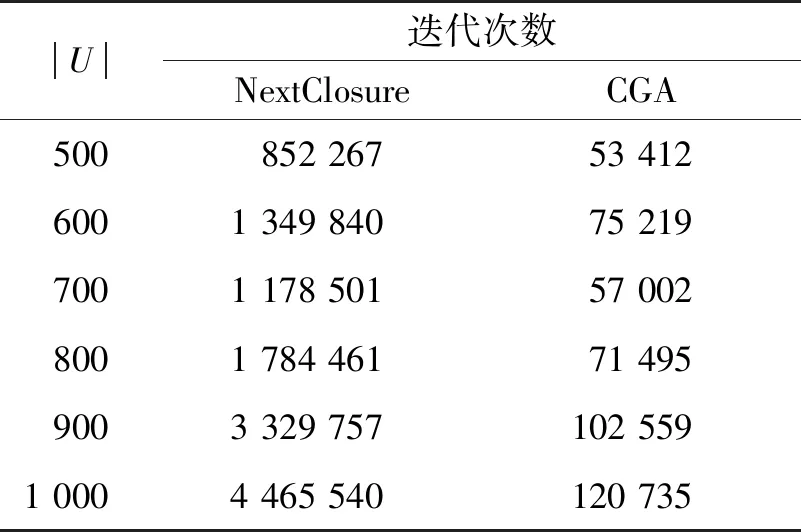
5.2 实验仿真及结果分析




6 结语

