一种基于优化驱动力矩的四杆机构的设计方法
王 勇 王红兵 张 驰
(珠海格力电器股份有限公司 珠海 519000)
引言
四杆机构的应用几乎遍及现代工业的各个方面,持续高速发展进的制造业对曲柄摇杆机构的机构尺寸、结构布局、运动特性及结构整体受力状况等提出了很高的要求,以适用于新型机械设备。经调研主要电器品牌,电风扇行业长期存在主要产品问题,风扇摇头过程中交变力突变大,摇头卡顿不平稳;运动机构设计较差,没有公开的完善可靠的设计与分析方法,导致市场整体水平不高。
双摇杆四杆机构[4]是风扇类产品摇头运动的最主要驱动机构,广泛应用于各类电风扇产品中,同样的也应用于各类有类似驱动目标的家电等产品上。书本学习的已知确定数直接推出求解都是一定确定的结果,实际设计中并不是,从机构各尺寸、安装方式,就连输出的设计目标,都是在一定范围内可变的,因此所有因素几乎都能够认定为变量,导致最终设计方案的不确定性。尤其对机构运行的稳定性和可靠性带来不可预估的隐患和未知。最终表现在产品上就出现了摇头存在受力突变极差较大,运行易卡滞,可能存在不同程度的噪音;长期后更易导致偏磨,导致机头不稳摇头不顺。
首先,常规电风扇摇头由四杆双摇杆机构实现。摇头机构子系统中曲柄、副摇杆、主摇杆、安装角度、主摇杆的摆动角度(后称为摇头角度)5 个变量,规定机架1 个定量;通过空间尺寸确定机架尺寸;除了安装角度以外的4 个变量利用机械原理理论[2]通过matlab 编程,在范围内穷举法输出满足设计目标的尺寸组合。主步骤示意如图1。

图1 方法步骤
其次,建立力学模型,利用ansys 对以上组合进行刚体运动力学仿真分析,输出每组受力曲线;首先,建立力学模型,对风扇摇头机构进行简化,将风扇的前后网以及风叶简化为有相同质量的圆盘,摇头机构转化为尺寸相同的双摇杆机构,电机与驱动电机转化为质量相同的质量点,以上对四杆机构所有可行性尺寸全面进行有限元受力分析。确定简化力学模型:
最后,对安装角度的范围进行分析并统计输出统计结果,确定整个系统的最优解。根据设计要求,即摇头角度需求、摇头对中,以及确认的主摇杆长度等要求,对摇头机构尺寸设定范围,曲柄、机架、副摇杆、主摇杆、摇头角度的范围,通过matlab 编程,输出满足摇头角度等要求的尺寸组合。选取其中符合要求的组合进行分析,最终确定设计方案。
1 确定双摇杆机构具体尺寸
在研究过程中,根据摇头角度的需求,初步确定各个尺寸范围,使用matlab 软件根据摇头角度需求,尺寸范围,编写程序,才能输出满足要求的尺寸组合。
根据摇头角度以及摇头机构的尺寸范围的要求,以及满足双摇杆机构的条件[3],通过编写相关程序,采用matlab 软件计算出满足要求的摇头机构的尺寸组合。根据设计要求,即摇头角度需求、摇头对中,以及确认的主摇杆长度等要求,对摇头机构尺寸设定范围,曲柄(10 ~14)mm,机架(18 ~22)mm,副摇杆(63 ~83)mm,主摇杆73.1 mm,摇头角度(72 ~76)°,通过matlab 编程,输出满足摇头角度等要求的尺寸组合。matlab 程序以及得出的尺寸组合如图2 所示。

图2 matlab 程序
排除部分远离设计目标的的尺寸组合后,对不同尺寸组合进行仿真分析,得出驱动电机所受的交变力,比较交变力峰值大小,选取最优的尺寸组合。选取以下尺寸组合进行受力仿真分析,研究驱动电机轴受力的变化曲线。
2 有限元受力仿真分析
针对风扇去除不必要的因素,需对仿真模型进行优化,根据主要双摇杆机构的尺寸,以及风扇机头相关的质量,简化风扇摇头模型,设置相关约束和转速等,仿真驱动电机所受的交变力,确定机构模型如图3 所示。

图3 简化摇头机构模型
根据风扇实际俯仰角,调整重力的方向,根据风扇实际摇头的转速,一般为(15 ~30)s 运转一个周期。根据风扇摇头机构的连接方式,设置仿真双摇杆机构的约束方式,旋转约束和固定约束,计算可得出的驱动电机所受交变力,交变力曲线如图4 示意。

图4 交变力曲线
根据以上方法对第一步得出的所有相关尺寸组合全部采用ansys 仿真分析[5],分析驱动电机轴受力情况。从图5 受力峰值差变化曲线可知,受力较小的有第11、14、15、16、18、20、21 组,结合摇头角度大小,摇头对中等情况,以及两个极限受力值的差值,暂选定第21组,曲柄12 mm,副摇杆74 mm,机架20 mm,主摇杆73.1 mm,完成4 个主要变量确定。

表1 尺寸组合[1]
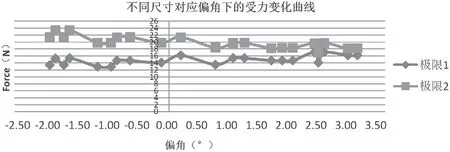
图5 峰值差变化曲线[1]
3 确定安装角
风扇机头重力方向固定,为了分析安装角度前移后移的影响,通过调整运动机构的安装角度,采用副摇杆74 mm,曲柄12 mm,机架20 mm,摇头角度75 °,主摇杆73.1 mm,分别(0 ~90)°范围分析驱动电机受力结果如图6 所示。从移动角度与受力的关系曲线可知,随着角度的增加,摇头极限1 受力先减小后增加,基本成线性变化,摇头极限2 受力先增加后减小。

图6 副摇杆长度变化对受力的影响曲线
1)从受力曲线可知,驱动电机受交变力,在两个摇头极限位置,受力出现极值。
2)从移动角度与受力的关系曲线可知,随着角度的增加,摇头极限1 受力先减小后增加,基本成线性变化,摇头极限2 受力先增加后减小,移动角度超过40 °后,受力变化较缓。
3)移动角度越小受力越小,移动角度尽量不要超过摇头角度的一半,确定最优值为(0 ~2.5)°。
4 分析副摇杆长度的影响
由选中副摇杆74 mm,曲柄12 mm,机架20 mm,摇头角度75 °,主摇杆73.1 mm,右角比左角大5.4 °。为了使得摇头对中,以及研究副摇杆长度的影响驱动电机的受力情况。分析结果如图7。
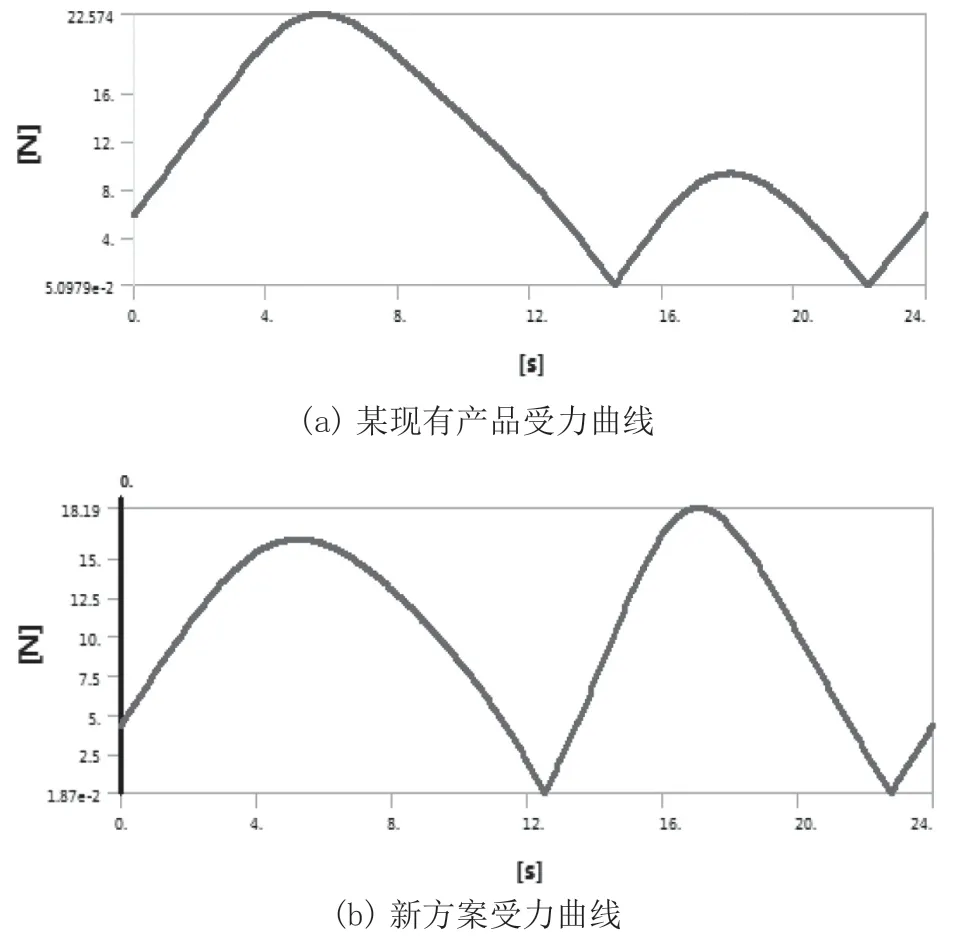
图7 分析结果
随着副摇杆长度的增加,极限1 位置受力最大值不断减小,极限2 位置受力最大值不断增加。副摇杆长度74.6 mm 相比74 mm,虽受力峰值略高,但偏角小摇头更加对中,确定副摇杆长度74.6 mm。
5 输出结果
综上所述,最终选取的机构尺寸曲柄12 mm,副摇杆74.6 mm,机架20 mm,主摇杆73.1 mm。此新方案受力峰值18.2 N,受力差值2 N,对比某产品现状,受力峰值22.6 N,受力差值13 N;摇头电机力矩改善19.5 %,有效改善驱动电机载荷,机构运动稳定性更优可靠性更佳。
6 总结
本文介绍了一种基于matlab 和ansys 优化驱动电机输出扭矩的四杆机构设计方法,实例将普通风扇摇头运动的双摇杆机构的基础优化与运动学仿真分析结合成综合性的设计方案,从而提升并验证其摇头运动的综合机能。设计出目标范围内的最优机构,实现可靠性是设计出来的。解决了多变量运算中无数解无数方案而仅凭想象盲目设计、无法判断可靠性、不能设计校验的问题。根据以上对双遥杆机构的设计介绍,可进一步同样应用至其他相关四杆机构的设计。

