指显平台对水下目标航迹异常值的实时处理方法∗

孟庆松 曹淑艳

（91388部队 湛江 524000）

1 引言

指显平台需实时接收各种测量设备按特定时间间隔发送的各类水下目标的位置信息，并实时、准确地显示目标航迹。复杂多变的水声环境和随机干扰等因素会导致测量的目标位置信息出现较大的随机误差，这些位置信息偏离真值较远、影响航迹正常处理和显示，被称为野值或异常值［1］。异常值的出现可能造成目标估计轨迹出现发散［2］。在进行多源的数据融合和航迹平滑处理前，需完成航迹异常值的判定和处理［1，3～4］。

由于水下环境复杂，测量误差与目标在单个测量周期内行进的航程处于相同数量级，且设备测量目标位置信息的周期长，同时，测量信息在传输到指控平台的过程中常出现中断与乱序，使现有的野值剔除算法难以应用。即使在不出现因网络传输原因中断、乱序的情况下，将一些较为成熟的算法如基于五点线性预测法［1］、牛顿插值法［5］、Kalman滤波［6～7］等方法应用到水下目标航迹野值处理时效果也不佳。

现有的较成熟的方法通过最小二乘法、卡尔曼滤波等利用目标的历史位置信息得到下一次测量时刻的估计位置，解算估计位置与测量位置的差值，并将差值与设置的阈值进行比较，若差值大于阈值即判定为野值，然后用估计值代替测量值，完成野值的剔除［8～12］。将这些算法应用于水下目标时，出现算法稳定性较差的问题，易出现异常值判定错误，特别是当一个或多个测量值数据不稳定或误差较大时，在用估计值代替测量值的过程中易出现航迹偏离的结果。其原因主要为估计位置受水下目标测量值的较大误差影响出现不稳定不准确的结果，且阈值设置未考虑到目标位置信息的测量周期较长和水下目标的运动特点等情况。

本文为提高指显平台对各类水下目标航迹野值的实时剔除与处理能力，提出了一种五点与九点结合的线性预测法对野值进行判定和处理，考虑到了测量信息中断、乱序带来的影响，并综合测量设备精度、目标机动能力、测量间隔时间等设置动态变化的阈值，最后，为防止因多个连续测量值出现较大误差等原因导致野值处理后航迹偏离，对连续判定为野值的位置信息进行再次实时分析以实现正确航迹的恢复。

2 数学模型

为便于计算，指显平台已将接收到的某测量设备按固定时间间隔发送的水下目标位置信息实时转化为笛卡尔直角坐标系下的位置和时间信息（xti，yti，ti），将选定海域近似为平面，xti为沿经度方向的位置信息，yti为沿纬度方向的位置信息，单位均为米，ti为与位置信息对应的测量时刻信息，i为整数序列，ti+1-ti为固定值Δt；σ为测量设备测量随机误差的标准差，单位为m。经过异常值判定与处理后，笛卡尔直角坐标系下的位置和时间信息可再转化为经纬度坐标进行显示。

指显平台实时接收到的目标位置信息可能存在单个或连续的异常值，且可能会出现中断、乱序等情况。

3 航迹异常值处理方法的整体流程

航迹异常值处理方法的整体流程见图1。

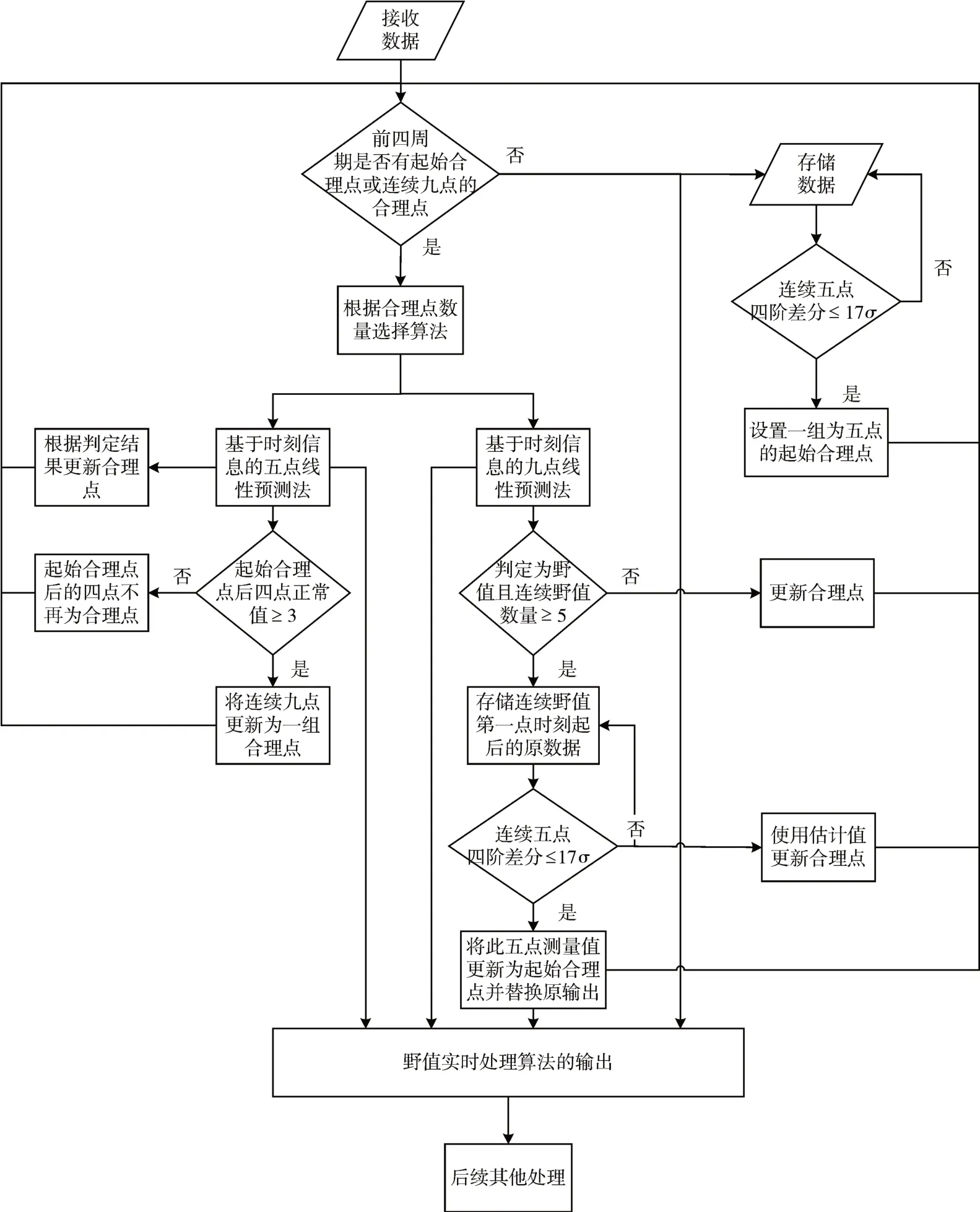
图1 航迹异常值处理方法的整体流程

4 五点与九点结合的线性预测法

4.1 一组合理点的选取

刚开始接收目标位置数据时，不进行判定，将数据实时输出，并进行存储，在存储区内，将各位置信息按测量时刻先后排列，并把每测量周期连续的五点编为一组，五点完全一样的不再重复编组，按组的时间先后顺序计算每组的四阶差分值。

其中Δ4xtj为经度方向位置信息的四阶差分值，Δ4ytj为纬度方向位置信息的四阶差分值；当|Δ4xtj|≤17σ，且|Δ4ytj|≤17σ时，将此五点作为一组起始合理点；不符合此条件时，计算下一组的四阶差分值，所有组均不符时，等待指显平台接收到下一个位置信息后新的编组信息。

4.2 五点线性预测法到九点线性预测法的过渡

由于水下环境复杂、测量误差相对较大，且存在可能发生的中断、乱序等情况，五点线性预测法不能稳定地发挥作用，易导致异常值判定错误，出现异常值处理后的航迹偏离。因此，本文采用一种五点与九点结合的线性预测法，既能发挥五点线性预测法启动速度快的优点，又具有相当的稳定性。

得到一组为五点的合理点后，开始对后续数据进行判定并向九点线性预测法过渡。对起始合理点后四个测量时刻的位置信息进行野值判定与处理；当接收到新的位置信息时，根据其测量时刻采用如下算法。

当新接收点（xtj+1，ytj+1，tj+1）与其时刻前最近的合理点测量时间间隔为Δt时，新接收点前的一组合理点的时刻为tj-4，tj-3，tj-2，tj-1，tj，按以下公式计算tj+1时刻的估计值与。

1）当新接收点（xtj+1，ytj+1，tj+1）与其时刻前最近的合理点测量时间间隔为Δt时，新接收点前的一组合理点的时刻为tj-4，tj-3，tj-2，tj-1，tj，按以下公式计算tj+1时刻的估计值与。

将估计值与测量值的距离差与阈值M1比较，M1=3σ+0.5σ+0.5a(Δt)2，a为目标的最大加速度；若，则认为tj+1时刻的测量值为正常值，将其作为合理点，并将最近一组连续五点的合理点更新；若>M1，判定测量值为野值，用估计值替代该测量值完成野值的剔除，不对合理点进行更新。

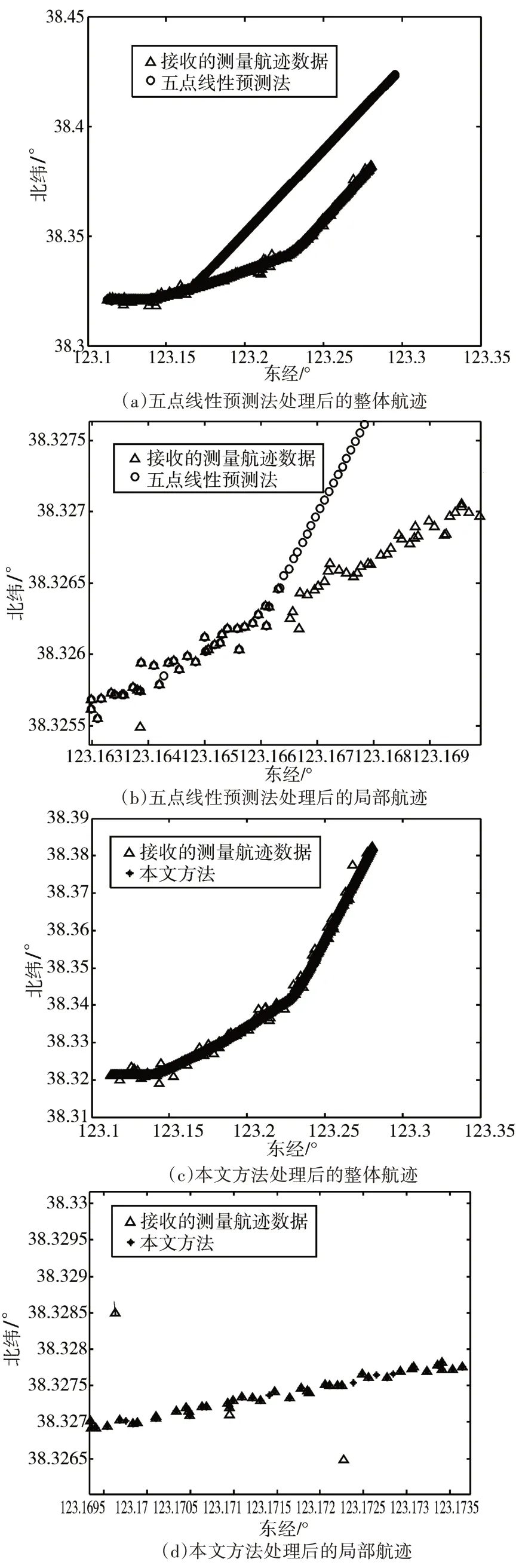
2）当新接收点（xtj+k，ytj+k，tj+k）与其时刻前最近的起始合理点测量时间间隔为kΔt（1

将估计值与测量值的距离差与阈值M2比较，M2=3σ+0.5kσ+0.5a(kΔt)2；若≤M2，则认为tj+k时刻的测量值为正常值，并对tj至tj+k间的时刻数据通过以下公式进行插值，其中，g为整数且0

将tj至tj+k间的数据其作为合理点，并将合理点情况更新；若，判定此测量值为野值，并用估计值替代该测量值完成野值的剔除，不对合理点进行更新。

3）当新接收点（xtj+g，ytj+g，tj+g）的时刻早于部分已接收点，其对应时刻的插值为，若，认为tj+g时刻的测量值为正常值，使用测量值更新此合理点的值，并用测量值替换原输出的插值信息；若，判定此测量值为野值。

接着根据起始合理点后四个周期的判定结果进行下一步计算，若起始合理点之后的四个周期中判定为正常值的数量已大于等于3，且指显平台已接收到起始合理点之后第五个周期的数据，可立刻将合理点更新为连续九点的合理点，若第九点仍未收到数据，使用式（3）、（4）得到估计值，将其作为合理点，转到下一步骤4.3节；若起始合理点之后的四个周期中判定为正常值的数量已小于3，则不再将旧的起始合理点之后四个点对应的数据作为合理点，同时等待一组为五点的新的起始合理点进行后续处理。

4.3 九点线性预测法

1）当新接收的点信息（xtj+1，ytj+1，tj+1）与前一合理点时间间隔为Δt时，此时刻的估计位置信息如下：

2）当新接收的点信息（xtj+k，ytj+k，tj+k）与前一点时间间隔为kΔt（1

3）当新接收点（xtj+g，ytj+g，tj+g）的时刻早于部分合理点，其对应时刻的插值为若，认为tj+g时刻的测量值为正常值，将测量值代替插值，替换原输出结果；若，判定此测量值为野值，仍用插值数据作为本点结果；

4）当步骤4.3 节1）中判定为正常值的次数和达到9 次，后续的每个点进行判定时，均使用重新计算的阈值，令R等于此时刻前最近9 个点r值平均值的0.5次方，r值即步骤4.3节1）中已计算出的测量误差的平方；对本步骤4.3 节1）与步骤4.3 节3），阈值M3=A+0.5σ+0.5a(Δt)2，A为3σ与3R的最大值；对本步骤4.3 节2），阈值M4=B+0.5kσ+0.5a(kΔt)2，B为3σ与3R的最大值。

5 航迹偏离判定与自动修正

当九点线性预测法最近一次判定（xtj，ytj，tj）为野值，且此野值对应时刻的前四个或四个以上测量周期时刻的数据均被判定为野值时，存储从连续野值的第一点时刻起以后的所有原始数据，从前至后对测量周期连续的五点进行编组，并用式（1）、（2）检验每组的四阶差分是否小于17σ，当某组四阶差分小于17σ时，计算此五点的平均速度。

将目标的最大速度作为阈值，当五点的平均速度满足小于阈值时，将此五点编组重置为起始合理点，不再将此起始合理点组前一时刻对应的值作为合理点，并在算法输出中用此五点的数据替换原对应时刻的数据。

6 仿真实验与性能分析

通过Matlab软件进行仿真分析，设置某水下目标初始位置为东经123.112152°，北纬38.321203°，航速在0 至10 节范围内变化，每0.5s 生成一位置数据，得到其仿真的10000 个实际点航迹。通过高斯分布为实际航迹添加误差，每1s～4s 选取一位置数据，得到仿真的测量位置数据。对仿真的位置数据，使其中5%的数据出现空缺或相近位置乱序，使其中5%的数据出现异常值，并使用传统的五点线性预测法和本文方法进行结果比较。

图2 五点线性预测法和本文方法的仿真结果对比

从仿真结果可以看出，五点线性预测法出现了数据处理后的航迹偏离，在相同情况下，本文方法能够实现实时的异常值处理，且未出现航迹偏离的情况。

7 结语

针对指显平台接收的水下目标位置信息常出现的中断、乱序以及设备测量周期较长等情况，本文给出了一种指显平台对水下目标航迹异常值的实时处理方法，首先对一组合理点进行判定和选取，然后采用五点与九点结合的线性预测法进行异常值的判定和处理，最后对判定为异常值的数据再次分析并实现错误判定时的航迹自动修正。仿真结果验证了本方法的可行性。本文方法计算量小，能够完成信息的实时处理。