基于辅助信息补偿和控制信号编码的重放攻击检测方法

张正道 杨佳佳 谢林柏

信息物理系统(Cyber physical system,CPS)是结合传感、通信、计算和控制过程形成的复杂系统[1-2].CPS 互联而开放的运行环境,在极大提高运行效率的同时,也引入了大量安全漏洞[3].攻击者可以通过入侵传输通道并且修改控制信号或者测量信号等多种方式破坏系统的正常运行,造成严重损失[4].近年来,CPS 的安全性问题,特别是CPS 的攻击检测问题,已经成为学术热点问题[5-7].

CPS 遭受的网络攻击主要包括拒绝服务攻击(Denial-of-service attack,DoS)、虚假数据注入攻击(False data injection attack,FDI)和重放攻击(Replay attack)等3 种类型[8].DoS 攻击的主要目标是阻止系统控制信号或者测量信号的正常传输,实现对系统控制性能的破坏[9].DoS 攻击的检测可以通过网络安全领域的检测方法实现.FDI 攻击和重放攻击主要由内部人员发起,属于“合法用户取得非法权限”,仅通过网络安全的手段难以预防.

FDI 攻击的主要特征是攻击者构造一个虚假数据替换系统的真实数据,从而引导控制器发出错误的控制指令,最终造成控制系统的性能退化或者瘫痪[10-11].重放攻击的主要特征是攻击者利用存储的系统历史时刻数据替换系统当前时刻的真实数据,进而引导控制器发出错误的控制指令.与FDI 攻击相比,重放攻击的攻击者无需预知控制系统的知识.同时,由于攻击者重放的通常是系统在稳定状态的测量数据,本身具有隐匿性,常用的攻击检测器难以检测[12].现有文献对重放攻击检测研究相对较少,开展重放攻击检测研究意义重大.

现有的重放攻击检测大致可分为添加水印和信号编码两类.虽然本质上都是向控制信号或者测量信号中添加额外的随机信号,但是信号编码方法在添加随机噪声后,还需对测量信号进行相应解码操作.文献[13]研究了测量信号编码的方法,系统遭受重放攻击后,利用编码和解码信息间的不同步检测攻击.为了提高检测率,测量值编码信息的方差可能会很大,甚至远超系统测量信号,使解码操作变得困难.此外单纯的噪声编码信息也容易被攻击者识别,进而实施可以避开相关检测的隐匿攻击.文献[14]最早提出向控制信号中持续添加高斯随机噪声,以使攻击前后的数据残差出现明显变化,并据此检测重放攻击的方法.但该方法改变了系统的最优控制信号,需要以牺牲系统控制性能换取攻击检测率.文献[15]进一步给出了所加高斯噪声方差大小与性能损失之间的线性关系,并且基于期望检测性能和允许控制性能损失提出了相应的最优化问题.为了减少所加噪声造成的系统性能损失,文献[16]提出将原本持续性加入的水印信号改为周期性加入.然而,该方法在减少性能损失的同时也降低了攻击检测率.文献[17]针对系统建模信息不完整造成建模有误差的情况,提出一种最优的在线控制水印信号设计方法.文献[18]针对系统可能存在数据丢包的情况,提出控制信号编码检测方法.针对不连续的重放攻击检测问题,文献[19]设计了一种周期性的水印添加策略,减少未发生重放攻击时的控制性能损失.考虑攻击者的重放延迟为任意值的情况,文献[20]提出了一种最佳周期性水印添加策略,在给定允许系统性能损失范围内调整加入控制信号的噪声大小和周期,以获得最高攻击检测率.但是,现有方法尚未明确给出检测率、性能损失和噪声方差之间的定量关系.

针对现有方法存在的问题,本文提出一种新的基于控制信号编码的重放攻击检测方法.为了减少加入编码信号对控制信号的累积效应,降低其对系统控制性能的影响,在向控制信号添加编码信号的同时,向状态估计端添加人为构造的辅助信号进行补偿.在卡尔曼滤波器估计状态值时仍使用未加入编码信号之前的最优控制信号.此时所添加的编码信号不参与控制信号的迭代过程.通过理论证明,给出了上述方法对重放攻击的可检测性以及检测率的定量表示.同时证明了相对于持续添加控制噪声的方法,本文方法具有更小的系统性能损失.最后,本文将编码信号方差、检测率和检测函数阈值之间的关系表示成一个可解的最优化问题,给出了求解编码信号方差的明确方法.通过仿真实验,验证了所提方法的有效性.

1 问题描述

1.1 系统模型

考虑CPS 的受控对象为一个线性定常系统,采用卡尔曼滤波器得到系统状态的估计值,同时依据线性二次高斯控制器得到最优控制信号,实现闭环反馈控制.系统状态模型为

考虑系统的随机过程噪声和测量噪声,定义系统性能指标函数为

1.2 重放攻击模型

本文研究测量信号重放的情况.因此假设攻击者能够记录测量数据y0,y1,···,yk,同时可将实际传感器信号yk修改为任意值实施重放攻击通常分为如下步骤.首先,攻击者记录从时间km到km+T的传感器测量值yk,其中,T为攻击者记录数据的时间长度.一般情况下T足够大,否则,可通过将记录的数据连续重放以达到攻击目的.其次,从时间kn到kn+T,攻击者将系统真实的测量信号yk修改为之前时刻记录的值,即

2 攻击检测

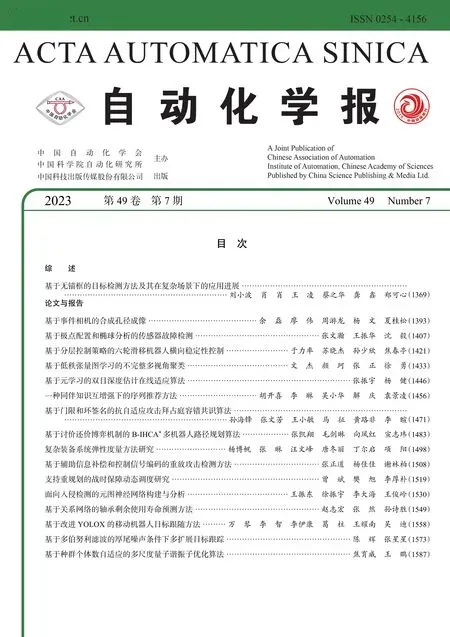
与现有控制信号编码检测方法不同,本文方法在添加控制编码信号的同时,向状态估计测量值输入端添加相应的补偿信号,从而减小编码信号对系统性能指标的影响,并且能使重放攻击前后检测信号出现明显协方差差异.图1 给出了本文方法的完整框图.

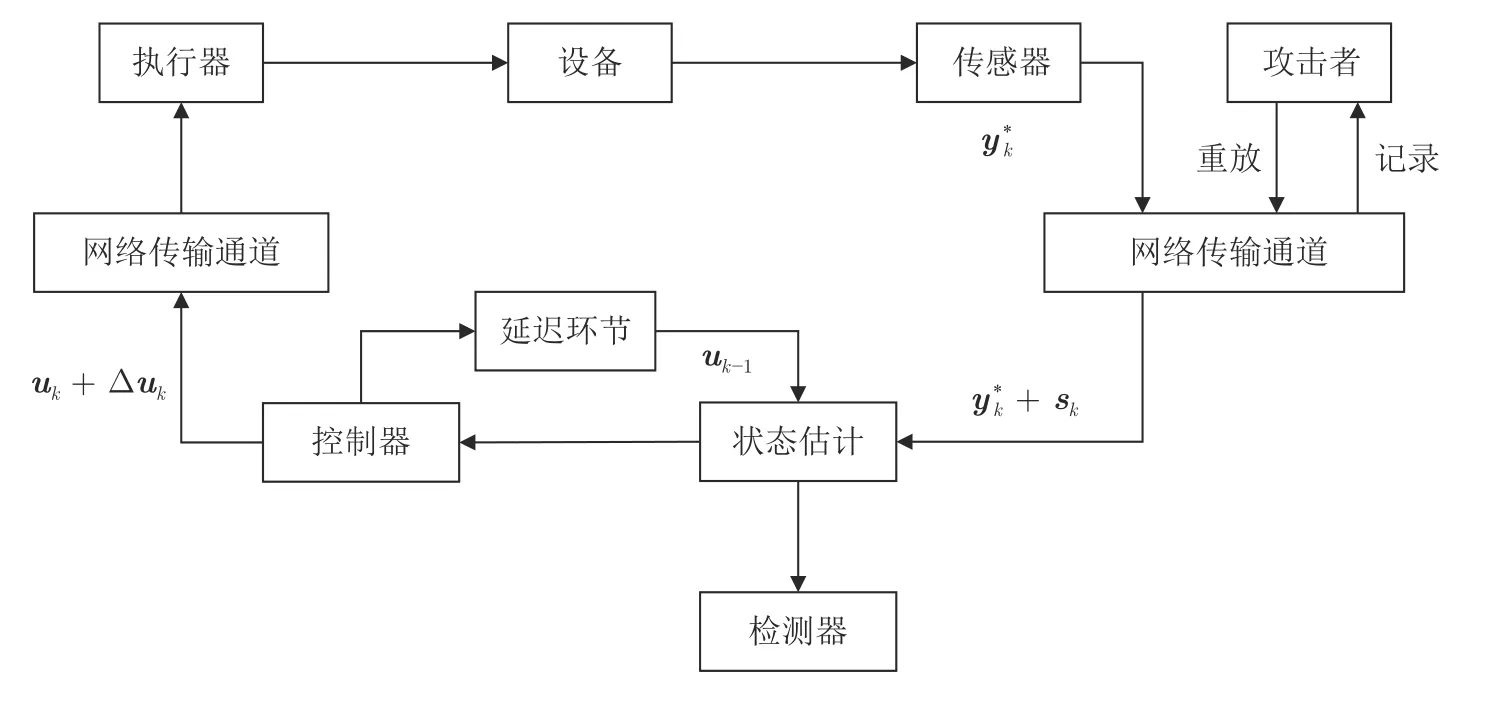
图1 本文所提方法的系统框图Fig.1 System diagram of the proposed scheme in this paper

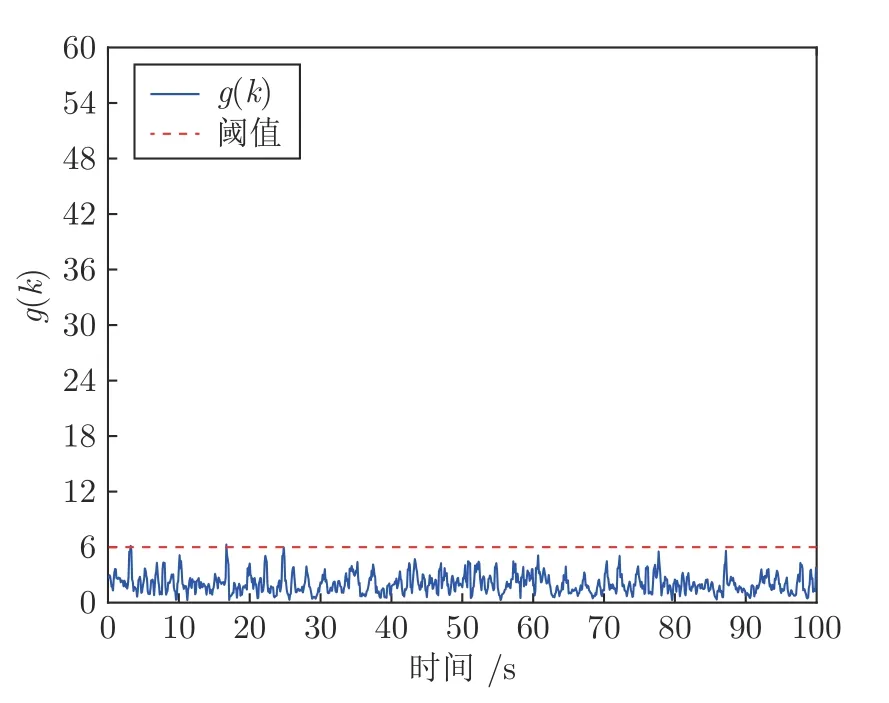
图2 直流电机系统正常运行时的检测函数曲线Fig.2 The detection function curve of the normal DC motor system

2.1 控制信号编码与辅助信号构建

由式(9)可知,此时估计端接收到的测量值与系统未加 Δuk时相同.

2.2 重放攻击的可检测性

定义检测信号rk为

结合引理1和式(10)可知,本文方案下的检测信号rk服从多变量正态分布 MVN(0,Σr).

构造检测函数为

式中,t为滑动窗口大小.显然,当系统未受攻击时,g(k)服从自由度为m的χ2分布.

定理 1.如式(1)所示线性定常系统,定义检测函数如式(12)所示,采用第2.1 节所提方案对控制信号进行编码.若加入的编码信号满足Δuk-1-ii0,···,k-1,则当系统遭受重放攻击后,攻击是可检测的.

其中,g′(k)是k时刻系统若处于正常情况下的检测函数值.

由于系统建模误差或者状态估计误差的存在,使用定理1 会导致误检发生.为此,可以给定一个检测函数的阈值τ,以及如下假设检验: 若g(k)＜τ,则表明系统处于 H0(正常)状态,反之则处于 H1(受攻击)状态.此时,本文方法对重放攻击的检测率满足定理2.

定理 2.如式(1)所示的线性定常系统,采用如式(12)所示检测函数和第2.1 节所提方案,则一定存在检测函数的阈值τ,使得在未发生重放攻击时,检测函数满足g(k)＜τ;而当系统遭受重放攻击后,检测函数增大,且满足ga(k)＞τ.此时,重放攻击检测率最大为

其中,Φ(·) 为标准正态分布的概率分布函数.

3 系统性能损失与检测最优化

控制信号编码方法需要在系统的最优控制信号加入随机的控制编码信号,从而造成了控制性能的损失.

式(26)表明,之前时刻向系统中添加的编码信号 ···,Δuk-2,Δuk-1会影响下一时刻的最优控制信号uk,且编码信号的添加对控制信号有累积效应,导致系统控制性能持续下降.

为了分析本文所述编码方法造成的性能损失,首先给出定理3.

定理 3.如式(1)所示的线性定常系统,在向系统控制信号中多次添加编码信号Δui,i1,···,k时,本文所提控制编码方法下,系统k时刻的控制信号只与当前时刻加入的编码信号 Δuk有关,而与历史编码信号 Δui,i1,···,k-1 无关.

证明.由第1.1 节可知,系统在k时刻的最优控制信号为

3.1 性能损失分析

定理 4.如式(1)系统,定义性能指标如式(4),则本文方法下,系统的平均性能损失不大于单次控制编码信号造成性能损失的最大值,且小于在向系统多次添加编码信号 Δui,i1,···,k时系统的性能损失.

证明.如第1.1 节所述,记xk为未加 Δuk时的正常系统真实状态,ek为未加 Δuk时正常系统的状态估计误差,ζk为添加了 Δuk前后系统的真实状态之差.现构造如下增广状态向量

所以本文方法的平均性能损失不大于单次控制编码造成的性能损失最大值.

记多次向控制信号中添加噪声信号方法的性能指标为J1,可得式(32) (见本页下方).

所以,在给定的 Σu相同的情况下,本文方法的性能损失小于向系统中多次添加控制噪声的方法.□

3.2 编码信号的确定

由式(17)可以看出,为了有效地检测出攻击,加入系统中的 Δuk应越大越好.然而,此时的系统性能损失也就越大.为了在二者之间找到一个平衡,提出定理5.

定理 5.针对如上假设检验,记攻击检测误报率(False alarm rate,FAR)为α,检测率(Alarm detection rate,ADR)为β,正常情况下与受到重放攻击后检测信号的协方差分别为Σr和则编码信号的协方差Σu和检测阈值τ满足如下最优化问题:

证明.由第 2.2 节可知,正常情况下检测信号的协方差 ΣrCP CT+V,系统遭受重放攻击后,协方差为

根据检测要求,误检率RFAR需满足

此外,检测率RADR需满足

由式(39)可以看出,式(38)成立只需

4 仿真实验

在本节中,使用MATLAB 的网络控制系统仿真平台Truetime 进行实验.以直流电机为例进行仿真验证,根据电路原理和刚体旋转定律,可得到如下状态空间模型

采用文献[21]中的参数,将上述系统按采样时间 0.1 s进行离散化,同时,考虑过程噪声wk和测量噪声vk,可得

其中,wk～MVN(0,W),vk～MVN(0,V),且协方差矩阵WVdiag{0.001,0.001}.

现假设攻击场景1 为: 前60 s 系统运行正常,攻击者记录了20.1 s～ 60 s 的测量数据,并在60.1 s开始重放记录的数据;假设攻击场景2 为: 系统从70.1 s 开始重放40.1 s～ 70 s 的数据.检测结果如图3和图4 所示.由图3和图4 中可以看出,重放攻击发生后,系统检测函数明显增大并且很快超过了正常阈值,由此可判定系统遭受了攻击.并且由图中曲线可见,针对不同重放数据长度和重放时间下的攻击,本文方法均具有良好的检测性能,检测率分别为83.75%和81.33%,误报率分别为3.15%和4.3%.对比设置检测率β0.75和误报率α0.05可知,本文方法的最终检测率高于设定值,而最终误报率低于设定值.这主要是因为在式(17)中计算受到攻击后的检测函数值时,忽略了交叉项,导致理论结果偏于保守.因此,实验所得攻击检测率略大于理论结果.

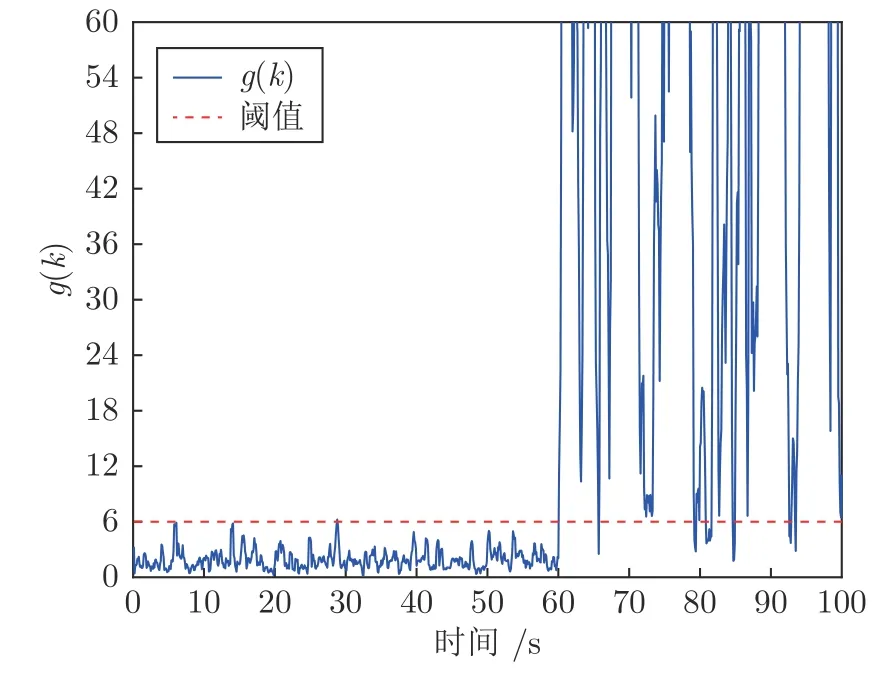
图3 攻击场景1 下的检测函数曲线Fig.3 The detection function curve under attack scenario 1

图4 攻击场景2 下的检测函数曲线Fig.4 The detection function curve under attack scenario 2

此外,本文考虑了系统遭受非连续重放攻击的情况.假设攻击场景3 为: 攻击者在第40.1 s和第70.1 s分别进行10 s 的测量值重放,检测结果如图5 所示,检测率为82.50%,误报率为4.75%.可以看出,本文所提方法对于非连续重放攻击也具有良好的检测性能.

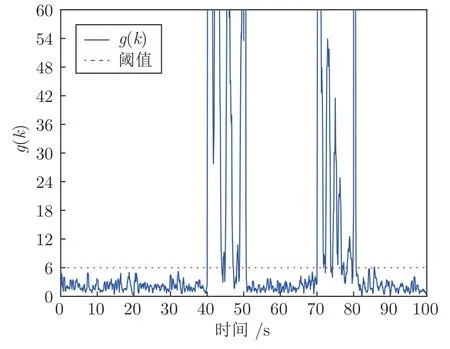
图5 攻击场景3 下的检测函数曲线Fig.5 The detection function curve under attack scenario 3

为了进一步验证本文所提方案的有效性,将本文方法与文献[15,17-18]中的方案进行对比,实验结果如图6和表1 所示.由于这些论文中并没有详细给出检测率与所加水印信号方差的具体关系,因此以下结果是重复50 次实验后得到的平均值.从图中可以看出,随着检测率的增加,不同方法的性能指标损失都逐渐增大,但在相同检测率要求下,本文方法的性能损失远小于对比方法.

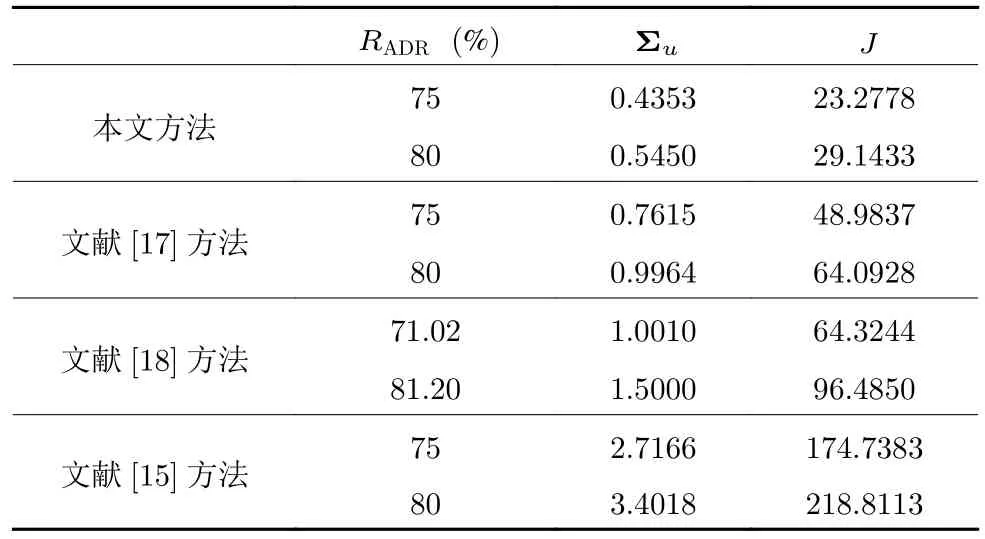
表1 噪声方差及性能指标比较Table 1 Comparison of noise variance and performance index of different schemes

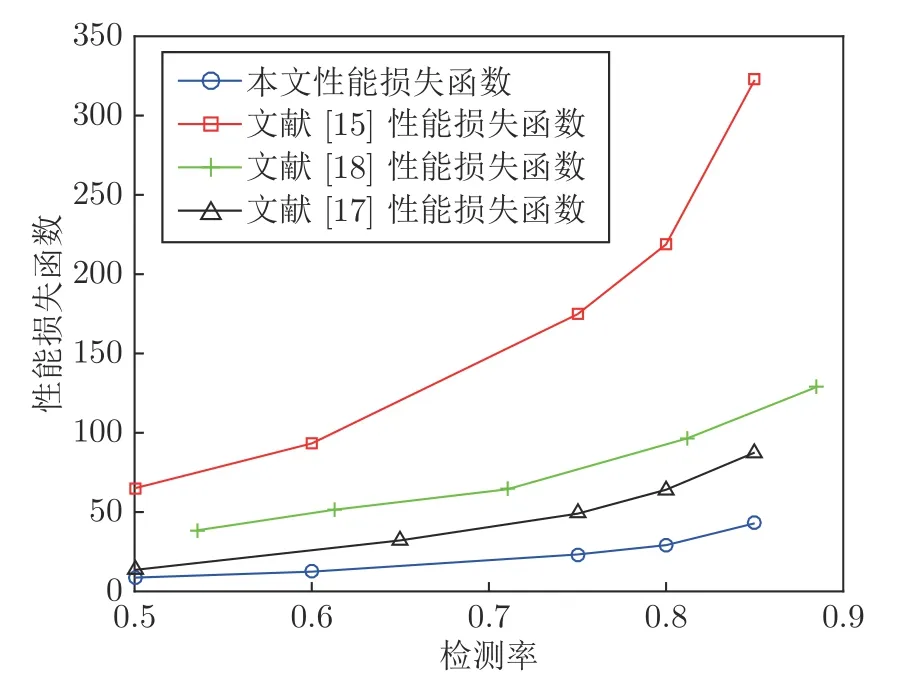
图6 本文所提的方法与不同方法的性能损失函数曲线对比图Fig.6 Comparison between the performance index of schemes in this paper and other papers

考虑系统可能受到非连续重放攻击的情况,与文献[20]方法进行简单比较.由于两种方法的前提条件不相同,因此,实验中仅在保证性能损失相同的情况下比较检测率结果.采用文献[20]中所用模型,通过采样周期Tsp2 s,将4 倍水箱控制系统离散化而得到系统参数.攻击者每次发动攻击的持续时间为:TsT0+X,其中,T0为基本时长,X ＞0为可控变量,且X的概率密度函数为f(X)ξe-ξX.现选取非连续攻击模型参数ξ1/5,T010,比较γ1γ2γ3时的情况.求取100 次仿真实验的平均结果,检测率定义为攻击时间内检测器报警次数的百分比.当采用周期水印策略为q/p0.5 时,即有50%的时刻控制信号加入随机噪声,此时系统性能指标值为J25 308,攻击检测率约为76%～ 77%左右.采用本文方法在保证相同性能指标的前提下,检测率为77.50%.采用周期水印策略为q/p0.8时,系统性能指标值为J40 404,攻击检测率约为86%～ 87%.采用本文方法,检测率为87.56%.文献[20]主要针对非连续重放攻击制定了攻击时间持续模型,并根据此攻击模型制定最佳周期水印策略,在给定允许牺牲系统性能范围内调整加入控制信号的噪声的周期,以求达到最高攻击检测率的同时控制性能损失较小.文献[20]所得结果是针对特定攻击模型下添加编码信号的最优周期,即控制成本也为最优.而在保证相同控制性能指标损失的前提下,本文仅采用均匀概率向控制信号加入编码,检测率略优于文献[20]所提方案,由此也可证明本文方法的有效性和优越性.

5 结束语

本文考虑了CPS 中重放攻击的检测问题,提出一种新的控制信号编码检测方法.证明了该方法对于重放攻击的可检测性和检测率上界.在保证较高检测效率的同时降低了对系统性能的影响,同时,给出了平衡检测效率和所需系统性能的最优化问题.实验结果表明,此方法能在牺牲较小系统性能的情况下有效地检测到重放攻击的发生.本文方法也可以与周期水印方法、随机水印方法等相结合,通过减少控制编码信号加入的次数,达到进一步降低系统性能损失的目的.