基于GA-SVM模型的大跨悬索桥主梁挠度预测研究
匡一成
(保利长大工程有限公司,广东 广州 510640)
1 基于PSO-SVM的大跨悬索桥挠度预测框架
1.1 支持向量机(Support Vector Machine,SVM)
作为一种适用于小样本分析的机器学习模型,SVM模型可有效克服常规拟合方法偏差过大和局部极值等问题,且泛化能力优于常规模型[10]。SVM模型主要包括输入层、隐藏层和输出层三层结构,通过n个非线性关系将输入层数据x映射到高维特征空间K中,并在K空间线性回归输出预测结果y,可在全局意义上逼近任意非线性函数,其结构示意图如图1所示。

图1 SVM结构示意图
给定一个数据集A={(xi,yi),i=1,2,…n},其中xi和yi分别表示输入样本和预测值,SVM拟合函数表达式为
f(x)=wφ(x)+b
(1)
式中:w和b分别为权重系数向量和常数;φ(x)为x的映射函数。
通过引入损失函数优化参数w和b,基于最小化风险原则,优化目标取极值表示为
(2)
式中:ξi和ζi代表松弛因子;C表示错误惩罚因子;ε表示损失函数,可引入稀疏数据点为决策函数,表示为
(3)
对于式(2),可通过Lagrange优化方法求解,对应有:
(4)

将式(4)回带到式(1),可得到函数f(x)
(5)
式中:K(x,xi)表示核函数,本文大跨悬索桥挠度预测采用精度较高的RBF核函数进行分析,表达式为
(6)
1.2 遗传算法(Genetic Algorithm,GA)
GA算法是一种借鉴生物界自然选择和遗传机制的优化算法,该方法由Holland学者于20世纪八十年代年提出[11]。该算法主要步骤为:(1)通过编码实现解空间转换为染色体空间;(2)设定进化代数、个体长度和种群大小等初始参数;(3)选择合适的适应度函数,计算种群中个体的适应度值;(4)针对种群进行选择、交叉和变异等遗传算子操作,使种群趋于最优方向进化,直到得到满足精度要求的解。
1.3 基于GA算法优化SVM的实现
由于采用SVM模型预测时,其核函数中r值和错误惩罚因子C可能影响SVM的泛化能力,进而导致预测结果存在一定的差异性。因此,可首先通过GA算法优化SVM中核函数r值和错误惩罚因子C进而采用SVM模型预测将具有更高的精度,其实现流程如图2所示,预测步骤为:(1)输入样本数据,并划分为训练样本和测试样本;(2)通过二进制编码,并对SVM的核函数类型、核参数和惩罚因子进行并随机产生初始种群;(3)采用GA算法优化样本参数,定义样本均方误差EMSE作为适应度函数,并计算个体的适应度值;(4)通过对种群进行选择、交叉、变异等遗传算子操作,产生下一代种群;(5)判断是否满足终止条件,即对种群个体进行适应度验证,若不满足,则继续采用GA算法进行优化,若满足则输出预测模型;(6)将最优参数输入到SVM模型中,进行预测模型训练并输出满足精度要求的预测模型。

图2 基于GA-SVM模型的大跨悬索桥挠度预测流程
1.4 基于GA-SVM的大跨悬索桥挠度预测流程及步骤
建立GA算法优化SVM的实现框架后,可进一步基于该方法进行大跨悬索桥挠度预测。类似的,首先通过大跨悬索桥实测数据或数值模拟获得训练样本,划分为训练集和测试集,随后通过GA算法优化SVM的r和C值,通过不断优化得到最优参数后,最后结合SVM算法网络训练(即公式(1)~公式(6)),最终形成预测模型用于挠度预测。因此,基于GA-SVM算法的大跨悬索桥挠度预测流程如图2所示,实现步骤如下。
步骤1:大跨悬索桥实测数据或数值模拟获得初始样本数据,本文通过数值方法,建立大跨悬索桥数值分析模型,获得对应节段的响应数据。
步骤2:选择大跨悬索桥已有各个位置的坐标作为输入样本,通过数值模型计算各坐标对应的挠度信息,形成输入输出样本集合。
步骤3:输入训练样本信息,基于GA算法不断优化SVM中核函数的r和错误惩罚因子C,以获得最优参数。
步骤4:基于SVM模型进行网络训练,得到满足精度的主梁挠度预测模型,进而预测悬索桥不同位置处的挠度水平。
2 算例分析
2.1 大跨悬索桥数值模型
为验证本文方法挠度预测模型的可行性,依托某大跨悬索桥工程,对其施工过程中竖向挠度进行预测研究。该悬索桥主跨和桥塔分别为1 500 m和200 m,两侧沿对称布置,基于通用有限元软件ANSYS APDL建立数值模拟。采用三维受拉/受压杆单元LINK10单元模拟主缆和吊索,拉压弯扭的单轴受力单元BEAM4单元模拟分配梁、加劲桁架和桥塔。对悬索桥两侧施加对称边界条件,桥塔底部施加固定约束;考虑恒载+活载工况,换算的荷载均布于主梁单元双主跨加载。求解时通过nlgeom命令打开大变形效应,sstif激活应力刚化进行求解。
2.2 结果评价指标
通过数值模拟获得大跨悬索桥样本数据后,可进一步结合GA-SVM法得到大跨悬索桥挠度预测模型。为合理评判其预测的准确性,将数值模型计算结果作为真实解,并因此残差指标衡量其预测精度,其表达式为
(7)

2.3 预测结果分析
据此,结合悬索桥数值模型获得的初始样本,并将初始样本划分为训练集和测试集,随后结合2.4节基于GA-SVM的大跨悬索桥挠度预测流程及步骤进行模型训练,最终获得满足精度的悬索桥主梁挠度预测模型,可预测不同位置条件下主梁挠度指标,并将测试集作为真实值进行对比。图3给出了本文大跨悬索桥在8/L(L为桥梁跨度)间隔位置的竖向挠度预测值和真实值的对比结果。由图3(a)可以发现,本文方法得出的挠度预测值在趋势上和真实值能达到很好的吻合,并且其变化规律符合结构力学影响线规律,预测结果在定性方面具有一定的可行性;分别将真实值和预测值设定为横纵坐标,并进行回归判定,其结果如图3(b)所示,可以发现,本文方法得出的挠度预测值和真实值大小维持在合理的范围内,其R2=0.997 2,具有较强的泛化能力,进行说明基于GA-SVM的大跨悬索桥挠度预测定量方面的有效性。

图3 预测值和真实值挠度对比曲线
表1给出了大跨悬索桥预测值和真实值残差指标,此处测点位置仍以8/L为间隔进行分析,可以发现,除2/L测点外,本文方法所得的挠度预测值同标准值残差指标εi均小于0.1的要求,进一步说明基于GA-SVM的大跨悬索桥挠度预测方法能很好的预测悬索桥挠度指标。而2/L测点位置ε=0.445,大于残差指标0.1以内的要求,说明GA-SVM方法仍有偏于局部最优解的情况,但从安全角度来看,预测值所得结果更大,更偏于保守,因此监测过程中采用本文预测值进行分析时仍切实可行。
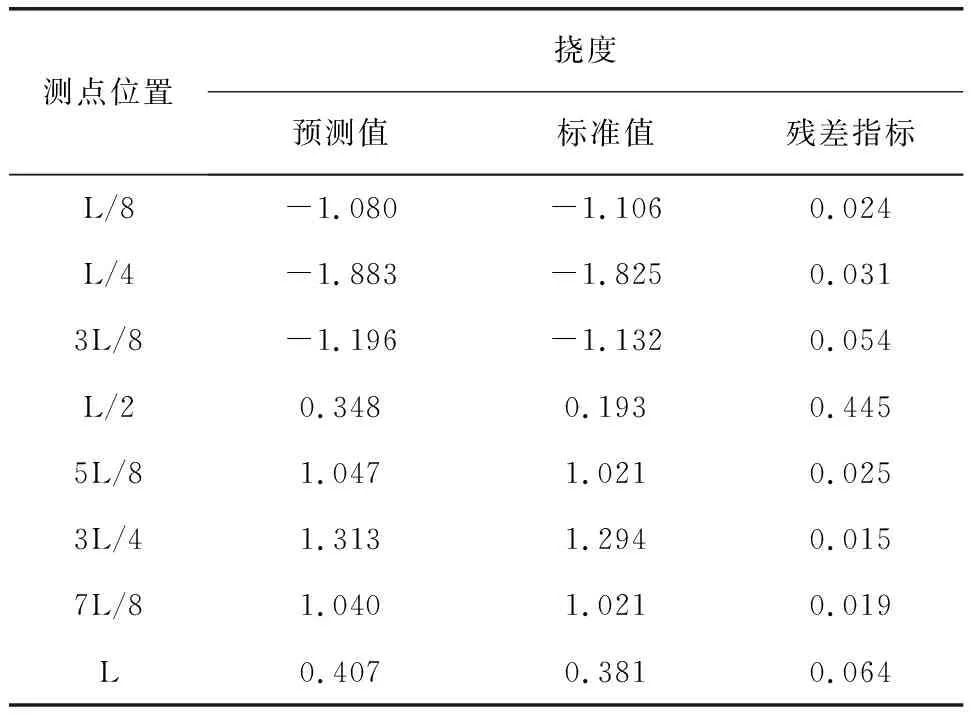
表1 大跨悬索桥预测值和真实值残差指标
3 结 论
大跨悬索桥挠度预测是桥梁评估以及健康监测领域的重要内容,其主梁挠度指标严重影响桥梁的运营安全。依托某典型大跨悬索桥工程,引入了GA-SVM方法应用于大跨悬索桥挠度预测,并验证了本文预测方法的可行性,得到主要结论如下。
(1)主梁挠度预测分析发现,基于GA-SVM模型的大跨悬索桥预测方法具有较高的精度,同真实值相比,其R2=0.997 2,并且绝大部分测点所预测的挠度结果残差指标均小于0.1,说明在趋势和数值方面均可达到的较好的吻合,可切实可行的应用于悬索桥挠度预测。
(2)残差对比发现,预测值中个别测点仍有发生局部最优解的可能,但本文方法所得的挠度预测值均相较于标准值略有偏高,从安全角度考虑,监测过程中采用本文预测值进行分析时更偏于安全。

