基于博弈论—云模型的露天矿边坡稳定性分析
许胜军,余华中,李德海,余永强
(1.河南理工大学 矿业研究院,河南 焦作 454000; 2.河南理工大学 土木工程学院,河南 焦作 454000)
露天矿岩质边坡稳定性评价一直是岩土工程界关注的热点问题之一[1]。当前,露天矿山石方开挖仍多采用爆破方式进行,随着采剥作业的不断推进,露天矿边坡岩体受开采扰动影响的损伤累计效应逐渐增强,边坡稳定性处于动态弱化过程,易发生边坡变形、滑移、垮塌等灾害性事故[2-3]。边坡稳定性评价是露天矿边坡工程研究的主要内容,其评价结果将对矿山生产安全和经济成本产生较大影响[4-5]。
针对露天矿边坡稳定性评价问题,相关专家学者进行了大量理论与实测研究,提出了多种评价模型和方法,取得了较为显著的成果。冯志楼等[4]基于实际地质勘察,通过考虑多重因素影响,采用不平衡推力法及有限元法对露天矿岩质边坡稳定性开展了数值模拟研究;李勇等[6]基于现场地质调查,通过将目标区域进行合理工程地质分区,并运用赤平极射投影法和全波列声波测井法,对矿山露天采场边坡进行了稳定性评价;张志军等[7]基于工程地质实测数据,构建了边坡岩体质量评价体系,建立了露天矿边坡稳定性极限平衡条分法分析模型;赵强等[8]为了分析地下开挖扰动对露天矿岩质边坡稳定性的影响,基于现场实测数据,建立了不同井下开采工艺影响下的露天矿边坡稳定性数值模拟分析方法;杜时贵[9]根据实际调查结果,通过理论分析,构建了露天矿边坡稳定性等精度评价模型和计算方法,实现了大型露天矿边坡稳定性等精度评价;赵志峰等[10]基于现场监测数据,综合考虑边坡稳定性评价体系与指标权重,结合突变理论,构建了岩质边坡稳定性综合评价模型。尽管上述研究成果对露天矿边坡稳定性评价作出了突出贡献,但考虑到影响边坡稳定性因素的复杂性及影响因素与边坡稳定性之间的非线性关系,使得上述文献中所涉及到的理论与模型在边坡稳定性评价方面仍具有一定的局限性,如突变理论与模糊数学理论模型较少考虑评价指标客观权重,侧重主观评价与指标相对重要性[10-11];可拓理论模型主要考虑主观权重,易忽略重要客观约束条件[12-15];耦合神经网络评价模型运算较为繁琐,评价过程复杂[16-17];距离判别赋权评价模型对样本数量要求较高,评价准确度难以控制[18-20]。基于上述分析,有必要对现有岩质边坡稳定性评价模型进行完善,以满足露天矿边坡稳定性简便、准确、合理评价的需要。
通过对传统层次分析法进行优化分析,结合熵权理论,分别计算模型评价指标的主观和客观权重,并根据博弈论理论求解边坡稳定性安全评价指标的综合权重;最后,引入云模型理论,确定评价指标的综合确定度,构建了基于博弈论的露天矿岩质边坡稳定性综合评价云模型,并与传统评价模型进行了对比,结合工程实测,证明了该模型的可行性和合理性。研究成果可为类似露天矿边坡工程的稳定性评价与防护提供理论参考和指导。
1 评价指标权重计算
1.1 主观权重的确定
层次分析法是确定评价模型中主观权重的常用手段,但其易受主观因素影响而使评价结果与实际情况存在较大偏差[12,21-23]。基于此,为使评价结果更加可靠,需对传统层次分析法进行优化,具体过程如下。
1.1.1 比较矩阵的建立
对比9标度理论,基于3标度理论构建的评价指标比较矩阵,具有计算简便易行、结果可靠等优点。按照层次结构模型,每一层元素都以相邻上一层次各元素为基准,按上述标度方法两两比较构造判断矩阵,设判断矩阵为B,按定义,具体如下:
(1)
对于两两比较得到的判断矩阵,解特征根问题:BW=λmaxW,所得到的W经正规化后作为因素的排序权重。可以证明,对于正定互反矩阵B,其最大特征根λmax存在且唯一,W可以由正分量组成,除相差1个常数倍数外,W也是唯一的。实际上,对B很难求出精确的特征值和特征向量W,只能求它们的近似值,采用方根法进行计算。
(1)判断矩阵B的元素按行相乘,得到各行元素乘积Mi(i=1,2,…,n)。
(2)
(2)计算Mi的n次方根。
(3)
(4)
(4)计算判断矩阵的最大特征根。
(5)
1.1.2 判断矩阵一致性检验
判断矩阵是分析者凭个人知识及经验建立起来的,难免存在误差。为使判断结果更好地与实际状况相吻合,需进行一致性检验。判断矩阵的一致性检验公式为CR=CI/RI。其中,CI为一致性检验指标,CI=(λmax-n)/(n-1),n为判断矩阵的阶数;RI为平均随机一致性指标。当CR<0.1时,一般认为B的一致性是可以接受的;否则,需要重新调整判断矩阵,直至满足一致性检验为止。
1.1.3 综合判断矩阵的确定
评价指标最优传递矩阵为:
(6)
(7)
则可推得评价指标综合判断矩阵为:
(8)
式中,cin=exp(rin)。
1.1.4 主观权重的确定
采用乘积方根法确定评价模型中的主观权重,具体计算方法为:
(9)
式中,wa为评价模型指标主观权重。
1.2 客观权重的确定
在评价模型中,为合理弱化主观因素对指标权重的影响,通常基于熵权理论来确定评价指标体系的客观权重。在评价模型中,评价指标的熵值越大,表明在系统中的重要程度越低,所占权重相应越小[24]。
假设n个岩质边坡安全评价指标中有m个原型观测数据,xij为第i评价指标的第j个原型观测值,构造矩阵X=[xij]m×n,归一化后得到矩阵Y=[yij]m×n。根据信息熵的定义,第i个评价指标的信息熵ei为:
(10)
求出各评价指标的信息熵后,即可确定各指标的权重ωi为:
(11)
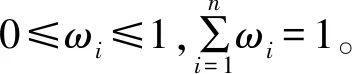
则岩质边坡稳定性评价指标的客观权重为:
wb=(wb1,wb2,…,wbn)T
(12)
1.3 综合权重的确定
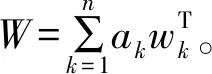
(13)
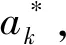
(14)
2 云模型理论综合确定度
云模型主要是通过理论分析,计算样本数据的隶属度,即确定度,进而解决样本的模糊性与随机性问题[25]。云模型是利用3个基本数字特征值表示的不确定性关系进行定性与定量转化的一种模糊概念模型[26-27]。
2.1 云模型的基本概念
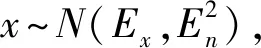
2.2 综合确定度的确定
根据云模型的特征,通过Matlab计算程序可生成模型单指标云图,进而可推得各指标在不同等级下的确定度,最后得出综合确定度为:
(15)
基于博弈论—云模型的边坡岩体稳定性综合评价模型系统如图1所示。
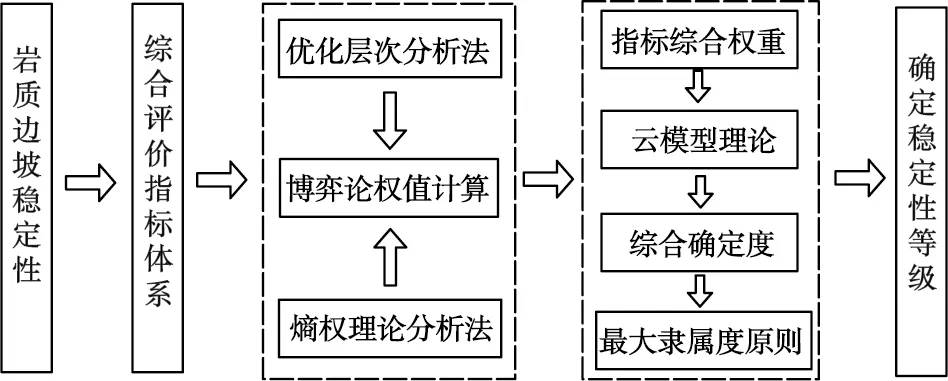
图1 基于博弈论—云模型的边坡岩体稳定性综合评价模型Fig.1 Comprehensive evaluation model of slope rock mass stability based on game theory cloud model
3 评价模型的构建
3.1 评价指标体系的确定
露天矿边坡岩体稳定性受多种因素的影响,其稳定性评价具有一定的模糊性和复杂性[29-30]。目前,岩土工程界针对岩质边坡稳定性影响因素及评价指标并无统一标准。根据建立的稳定性分级标准,所选择的岩质边坡稳定性影响因素应具备代表性、关联性、可量化、易获取及存异性5个原则特点[31-32]。据此,笔者所构建的岩质边坡稳定性评价体系中,影响边坡稳定性的因素主要包括工程地质因素、水文环境因素与工程扰动因素[33-34]。其中,工程地质因素主要包括单轴抗压强度X1、抗拉强度X2、杨氏弹性模量X3、内摩擦角X4、黏聚力X5、泊松比X6、岩体质量指标X7、边坡高度X8、边坡坡度X9;水文环境因素主要包括日最大降雨量X10、岩质边坡内部潜水量X11;工程扰动因素主要包括振动烈度X12、质点振动速度X13、震源距离X14。
根据露天矿边坡岩体所处的环境条件,其稳定性处于动态变化过程中[35]。因此,边坡岩体稳定性分级标准与其实际工况密切相关。根据工程岩体分类标准,边坡岩体稳定性可分为5类[23],分别为:极稳定(Ⅰ级)、稳定(Ⅱ级)、基本稳定(Ⅲ级)、不稳定(Ⅳ级)、极不稳定(Ⅴ级),具体分级标准见表1。
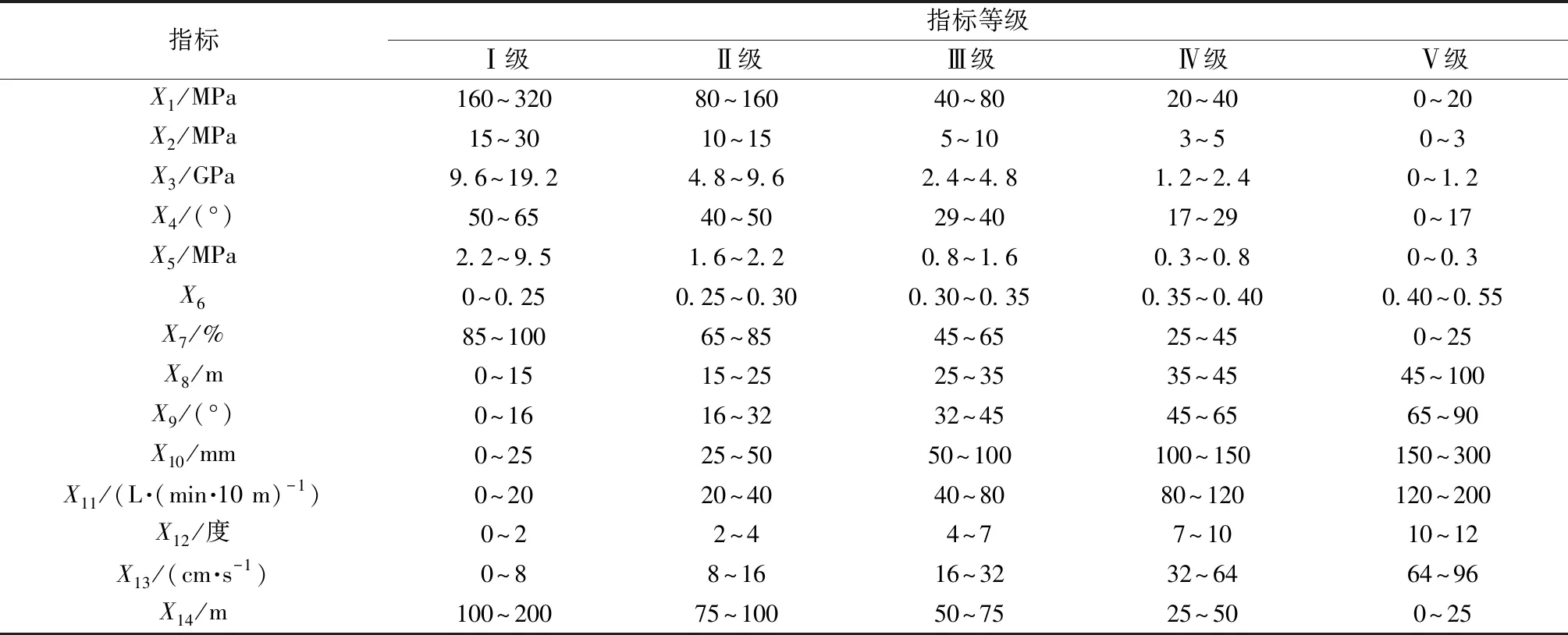
表1 不同评价指标条件下边坡稳定性分级标准Tab.1 Classification standard of slope stability under different evaluation indexes
3.2 评价指标云图
根据云模型的数字特征,结合表1,采用Matlab计算程序生成评价模型指标云图,典型评价指标云图如图2所示。其中,云模型数字特征计算公式见式(16),计算结果见表2。
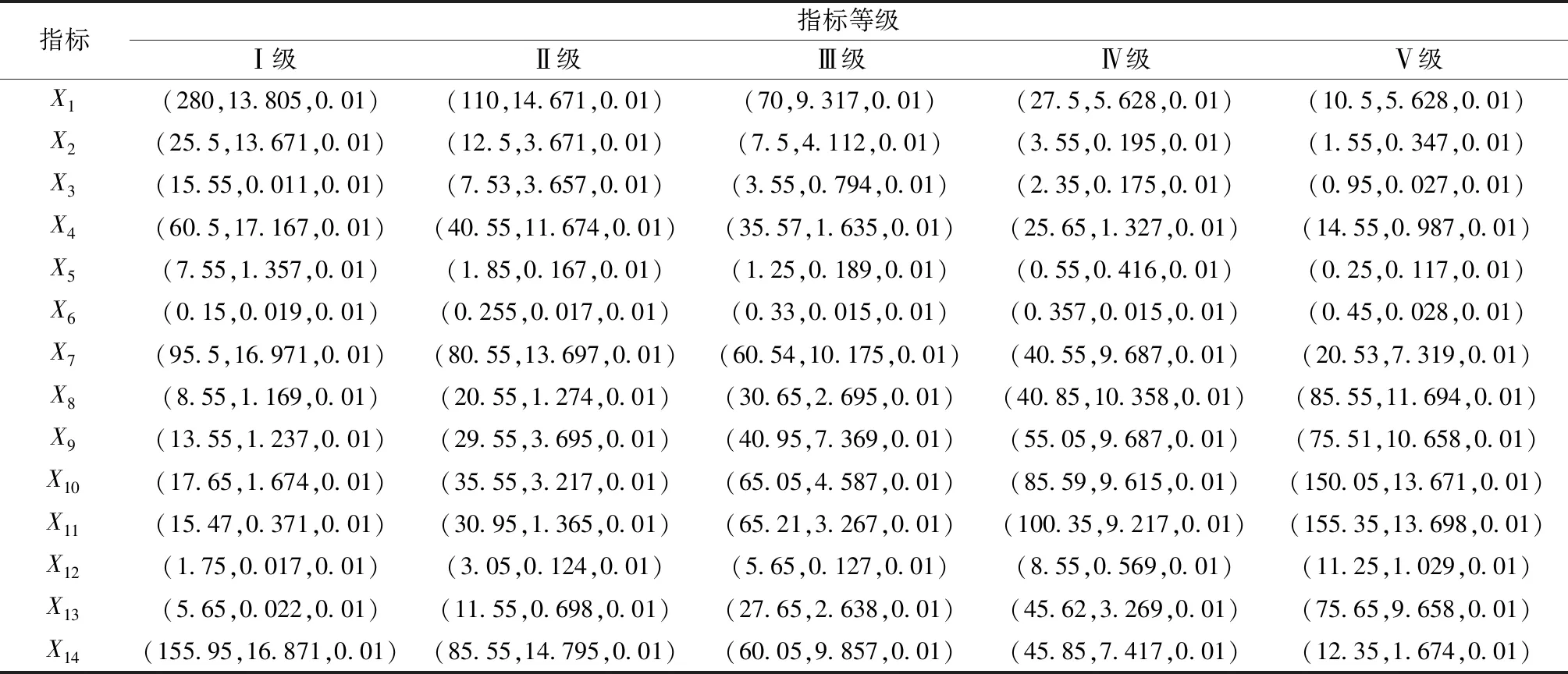
表2 评价指标云的数字特征值Tab.2 Digital eigenvalue of evaluation index cloud

图2 典型指标云图Fig.2 Typical index cloud chart
(16)
式中,cmax、cmin分别为评价模型指标等级划分中对应的最大、最小边界值;k为特征常数,取0.01。
4 实测验证
以青海某非煤矿山露天边坡稳定性为例,来验证文中所提出的基于博弈论—云模型露天矿边坡岩体稳定性综合评价模型的可靠性。选取4处边坡点,编号为边坡1—边坡4。其中,边坡1和边坡2岩性主要为白云质灰岩,经钻探发现,该边坡岩体层理发育较明显,层面平直粗糙;边坡3和边坡4平均坡度为64.5°,坡面整体较为稳定,边坡岩性均以白云质灰岩为主,层面胶结较好。根据地质勘探报告,总结得到相应边坡岩体物理力学参数与水文监测结果,见表3。

表3 露天矿边坡稳定性评价指标实测值Tab.3 Measured value of slope stability evaluation index of open-pit mine
4.1 指标权重的确定
4.1.1 主观权重的确定
由式(1)—式(5)可求出评价指标主观权重为:
w1=(0.136,0.037,0.041,0.029,0.107,0.039,0.021,0.074,0.109,0.042,0.051,0.068,0.064,0.012)T
4.1.2 客观权重的确定
根据表3可得到决策矩阵O为:
则由式(10)—式(12)可得指标客观权重为:
w2=(0.114,0.239,0.048,0.014,0.187,0.009,0.026,0.107,0.009,0.046,0.071,0.063,0.015,0.003)T
4.1.3 综合权重的确定
由式(14)建立指标最优组合系数方程组:
(17)
由Matlab对式(15)进行求解并归一化后可得:a=0.516,b=0.484。
基于博弈论,由式(10)可求出指标综合权重w为:
w=(0.037,0.109,0.091,0.117,0.047,0.102,0.096,0.067,0.104,0.098,0.073,0.149,0.185,0.101)T
4.2 综合确定度的求解
由式(12)求出的云模型特征参数,结合评价单指标云图,可计算出露天矿边坡岩体在不同评价指标不同等级下的单指标确定度,代入式(11)中,依据最大隶属度原则,可求出不同边坡岩体的综合确定度,见表4。

表4 露天矿岩质边坡稳定性等级评价Tab.4 Stability grade evaluation of rock slope in open-pit mine
由表4可知,根据最大隶属度原则,边坡1和边坡3岩体稳定性处于第Ⅱ等级,即稳定状态,但对第Ⅲ等级(基本稳定状态)有较大的倾向性。边坡2稳定性隶属于第Ⅲ等级,但对等级Ⅳ(不稳定状态)有较大的倾向性,根据表3可知,相较于其他边坡岩体,边坡2的X2(抗拉强度) 因素较小,但该影响因素所占权重较大。因此,对边坡稳定性有较大影响。边坡4稳定性处在第Ⅳ等级,但对等级Ⅴ(极不稳定状态)有较大的倾向性,同样由表3可知,相较于其他边坡,边坡4的X11(边坡内部潜水量)影响因素所占权重较大。因此,对边坡稳定性有较大影响。
采用灰关联分析理论、可拓学理论、人工神经网络和模糊数学理论对上述露天矿岩质边坡稳定性进行评价,并通过现场实际调查进行验证,所得结果与文中所构建模型评价结果相一致,表明博弈论—云模型的分析结果可靠,能够为露天矿边坡岩体稳定性评价提供理论指导。
5 结论
(1)考虑到传统层次分析法在评价指标主观权重计算方面的不足,通过对传统层次分析法进行优化改进,结合熵权理论,合理确定评价指标的主观与客观权重,并基于博弈论计算指标综合权重,能够使边坡岩体稳定性评价更为可靠。
(2)露天矿边坡安全状态具有模糊性和随机性特点,其稳定性分析属于动态系统工程,而云模型对处理随机性与模糊性问题具有突出优势,结合博弈论在评价指标权重分配方面的优势,将博弈论—云模型联合应用到露天矿边坡稳定性评价中,能够提高评价结果的可靠性,可以为边坡稳定性评价提供一条量化分析的新思路与新方法。
(3)从工程地质、水文环境和工程扰动3个层面选取了14个评价指标,建立了基于博弈论—云模型的露天矿边坡稳定性综合评价体系,但影响露天矿边坡稳定性因素较为复杂,且影响因素与边坡稳定性之间具有非线性和不确定性关系。因此,所建评价体系还有待进一步完善。

