基于水工混凝土抗压强度和弧面对压强度的试验分析

朱 冰

(盘锦市水利服务中心,辽宁 盘锦 124010)

为准确测定水工混凝土抗压强度许多机构研究提出小芯样检测技术,并先后形成抗剪法、抗折法和直拔法等方法,其原理都是以抗折应力、剪应力、直拔应力等小芯样试件物理量值来推测抗压强度[1-4]。这些方法对构件所造成的损伤较小且可以检测出构件内部的抗压强度,有效弥补了回弹法只能测定表面强度的不足,在一定程度上促进了混凝土检测技术的发展。但实践表明,推测的抗压强度值与此类技术检测的应力值相比高出几倍乃至十几倍,在推定抗压强度时测试应力值的微小变化都会被放大相依倍数,使得检测数据时常发生误判的情况。

为了使预推定的抗压强度值与试验测试物理量值处于同一数量级,解决“以小搏大”的问题,在保证内部强度检测精度及对混凝土损伤较小的情况下,工程检测领域提出一种弧面对压法检测技术[5]。该技术是在弧面对压试件侧面利用两个相对的弧形施压块加压至破坏,结合弧面对压力峰值确定相应的强度,其中弧形对压试件为直径38mm钻取自硬化混凝土钻的微小芯样。相较于以上小芯样类检测法,弧面对压法主要存在以下不同:①在设计原理上利用抗压变量-弧面对压应力直接测定强度,这使得数据随机性明显下降;②试件的抗压强度值与测试的弧面对压应力值处于同一数量级,从而解决了推定时误差放大的问题,这是弧面对压法确保数据检测精度的关键[6-7]。鉴于此,文章采用弧面对压试验和抗压强度试验测定C20～C80等级水工混凝土的7d、14d、28d、60d、90d龄期抗压强度,以不同拟合方式分析标准试件抗压强度与弧面对压强度的相关性,并进一步验证了弧面对压法的适用性和检测精度。

1 试验方法

1.1 原材料

试验选用海螺P·O4 2.5级和P·O 52.5级两种水泥,细度模数2.7的中砂,粒径5～31.5mm的连续级配花岗岩碎石,S95矿粉、硅灰及F类Ⅱ级粉煤灰,外加剂用聚羧酸高效减水剂,经检测各原材料主要技术指标均符合相应规范要求。

1.2 试验配合比

根据《水工混凝土配合比设计规程》及不同强度等级要求合理设计试验用配合比,控制拌合物坍落度处于160～220mm微调减水剂用量,如表1所示。

表1 试验配合比

1.3 制作与养护

参照《水工混凝土试验规程》中的操作流程将新拌混合物制成150mm×150mm×150mm的标准试件,入模成型后室内静置24h脱模,然后编号标记并移入标养室养护至规定龄期。为防止试验过程中试件被挪用、损坏或丢失,应保护好各组试件,试验配制试件数量如表2。

表2 试件制作数量

1.4 试验设备与方法

弧面对压试件钻制装置和弧面对压仪如图1所示。首先,在专用固定装置内放置混凝土标准试件,选择钻取面为浇筑面,保持浇筑方向与钻取方向相垂直。试件稳固后,启动钻机匀速钻进至钻深达到58mm,然后取出芯样标注试件编号与浇筑方向,弧面对压试件应满足长度≥58mm,直径处于(38±0.4)mm、30mm长度内最大偏差≤0.1mm且侧面顺直。

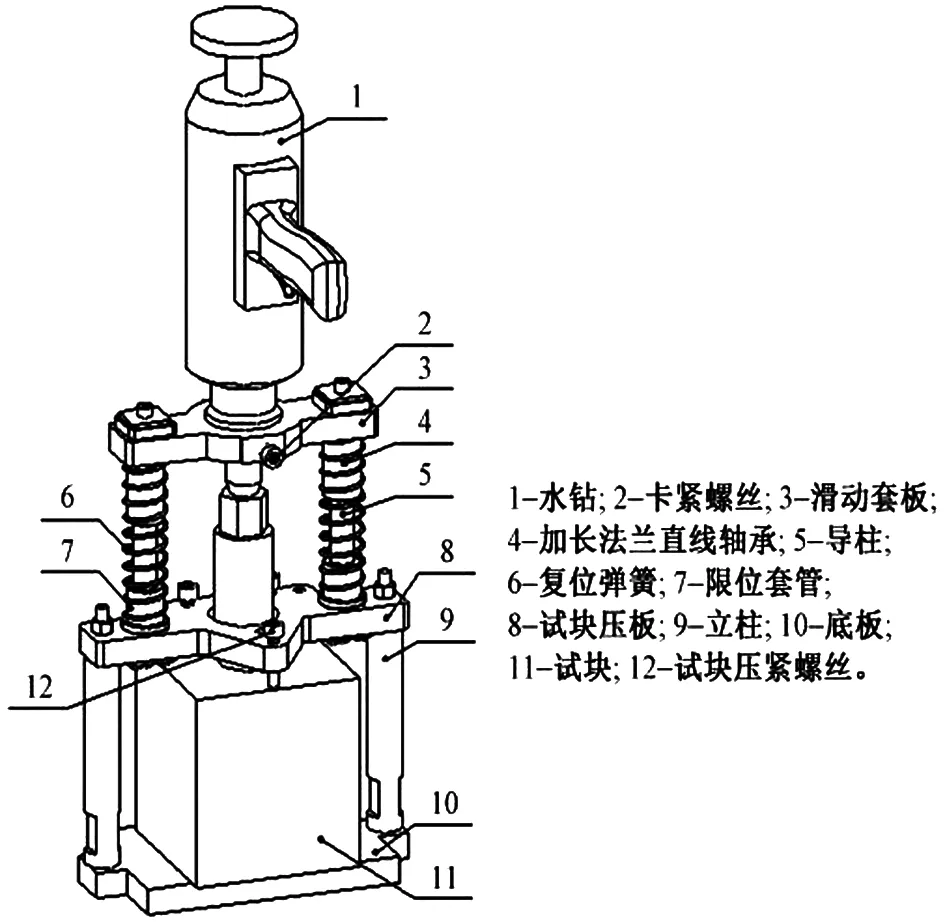
(a)钻制装置

实际使用时弧面对压仪符合以下技术参数要求:①测试精度0.01kN,测量量程0.00～100.00kN;②压力表具备维持峰值的功能,弧面施压块的开口尺寸为33.77mm,弧面高度、直径和弧长依次为31.00mm、39.00和1/3圆周长;③形成不低于10mm,设置电震装置,在试件间隙内的金刚砂(细度80～120目)能够在震动作用下饱满、均匀地分布。主要操作流程如下:

步骤1:在弧面对压仪试验空间内居中放置弧面对压试件,保持弧面对压试件侧面与施压块内部的间隙为2～3mm并用弹簧支架固定弧面对压试件。

步骤2:将金刚砂灌入弧面对压试件侧面与施压块内部间的空隙至溢出,启动开关震动5s使金刚砂饱满均匀。

步骤3:清零压力表并设置成峰值状态,控制施力干加载速率0.6～0.9kN/s,顺时针摇动加载至试件破坏。

步骤4:记录试件的弧面对压力值为试件破坏时的荷载值,精度为0.01kN。

1.5 数据计算

采用公式(1)将弧面对压力值转化成应力值,具体如下:

fa,i=Fi/A

(1)

式中:fa,i、Fi、A为弧面对压试件i的弧面对压应力,MPa、弧面对压力值,kN及其面积,mm2,直径为38.0mm时弧面对压试件的受力面积取1020mm2。

参照《水工混凝土试验规程》测定标准试件的抗压强度,结合各组试件破坏时的荷载值计算出相应的抗压强度值。

2 结果与分析

2.1 试验数据

将同龄期同强度的6个试件分别用于弧面对压强度和立方体抗压强度测试,每次测定3个试件取平均,并利用强度与破坏荷载转换公式计算相应的抗压强度,如表3、表4所示。

表3 弧面对压强度值

表4 立方体抗压强度值

2.2 数值回归分析

每组弧面对压强度值取该组3个立方体抗压强度所对应的平均值,并按照中值、最小值、最大值、中小值(最小值与中值的平均值)、大中值(最大值与中值的平均值)、大小值(最大值与最小值的平均值)、平均值(所有数据的算数平均值)的方式处理该组3个弧面对压强度所有数据。以弧面对压强度和立方体抗压强度为自变量、因变量,利用最小二乘法回归拟合数据,并通过对比各龄期弧面对压强度和立方体抗压强度数据,建立多项式、指数、线性和幂函数模型[8-10],如表5所示。

表5 回归分析

通过中值、最小值、最大值、平均值、中小值、大中值、大小值的数据处理方式和建立多项式、指数、线性和幂函数等数学模型拟,最终确定在多项式函数模型下立方体抗压强度与弧面对压强度的相关系数R最高达到0.9610,相对标准差18.2%,平均误差9.5%,能够达到精度要求[11-13]。最优测强曲线为多项式函数形式如图2所示,其数学表达式如下:

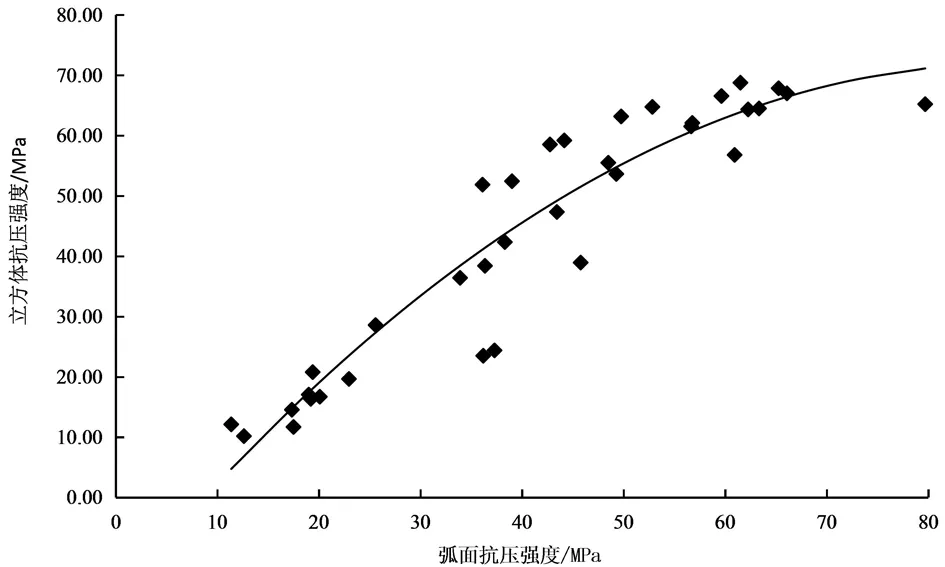
图2 最优测强曲线

fc,i=-0.0152fc,i2+2.1065fa,i-15.180

(2)

式中:fc,i、fa,i为立方体抗压强度和弧面对压强度,MPa。

3 结 论

采用弧面对压强度试验和立方体抗压强度试验测试不同强度等级及养护龄期下的水工混凝土抗压强度,经统计分析和数据计算,主要结论如下:

1)不同龄期及不同强度等级下水工混凝土的弧面对压强度与立方体抗压强度之间存在较好相关性,多项式、指数、线性和幂函数形式的相关系数均超过了0.90,这表明弧面抗压强度能够准确反映水工混凝土的抗压强度。

2)经对比分析,在多项式函数模型下立方体抗压强度与弧面对压强度的相关系数R最高为0.9610,最优测强曲线为多项式函数形式的fc,i=-0.0152fc,i2+2.1065fa,i-15.180。