多角度冲击工况下铝/CFRP复合管诱导槽多目标优化设计*

王登峰，卢春达，梁鸿宇

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

近年来，轻质高性能结构材料的应用成为汽车零部件的重要发展方向［1］。具有代表性的方法有变厚度辊压技术［2-3］、先进高强钢改性技术［4-5］、多胞结构化［6-8］和复合材料［9-10］等。其中，碳纤维增强复合材料（carbon fiber reinforced polymers，CFRP）具有高比强度和比刚度以及设计的灵活性，在汽车吸能部件方面具有广泛的应用前景。

然而，一方面CFRP 的成本较高［11］，另一方面，由于其明显的各向异性特征，在吸能过程中变形不稳定，不利于能量吸收［12］。鉴于此，有学者提出了金属/CFRP 复合结构，利用金属的渐进变形来诱导CFRP发生稳定失效，并在轻量化以及低材料成本方面展示出显著优势。

Zhu 等［13］对碳纤维包裹铝合金的复合管样件进行了轴向压缩试验研究，发现CFRP 层会产生较大碎片，导致CFRP 的抗撞水平降低，使吸能效率低下；而铝管在外侧时，内部CFRP 层则发生渐进式压溃，可以充分发挥其吸能潜力，使复合管的整体耐撞性显著提高。此外，Zhu 等［14］还通过试验和数值方法比较金属、CFRP以及复合管在斜向加载下的变形模式以及吸能特性。发现与CFRP 管相比，复合管可以降低加载角对能量吸收的影响。进一步地，Mamails 等［15-17］通过对CFRP 管的轴向压缩性能进行试验与仿真研究，发现纤维取向对其有很大影响。结果表明，［±90°］n铺层方案具有更好的能量吸收性能，且在初始分层之后表现出更高的弯曲刚度，相似的研究也被Kim等［18］开展。

值得注意的是，复合管在进行轴向压缩时峰值反力很高，针对金属/CFRP 复合管，如何进行合理的诱导结构设计，使其吸收能量稳定可控的同时，具有较低的峰值力是非常有必要的［19］。李晓南等［20］建立了复合材料增强铝方管的双层壳单元模型，通过仿真分析发现顶部设置诱导孔比设置 45°外倒角的诱导形式更能有效改善吸能特性。Hu 等［21］尝试在外侧铝管上进行诱导孔的设计，结果表明复合管吸能量要高于两种单管之和，且在相同的能量吸收下，复合管具有更高的结构利用率，在承载和能量吸收方面均有较大潜力。但是对于复合管开设诱导孔的形式，在压缩过程中，会产生不规则的变形模式，降低峰值力的同时，削弱了吸能稳定性。Hussein 等［22-23］对比了复合方管在V型压头与槽状缺口进行配合的诱导形式下的变形模式以及吸能特性，结果表明该方式降低了初始峰值力，且变形模式较为规则，但其局部位置的应力集中过大。这里需要指出的是，目前也有一些关于功能梯度设计的复合管结构，也取得了很好的性能提升效果。比如Ma等［24］采用CFRP进行梯度包裹铝方管，系统地分析了铝管厚度以及CFRP 缠绕角度在不同加载角度下对复合管耐撞性能的影响。结果表明，该种设计形式使比吸能相比纯铝管得到了大幅提升，但受工艺条件的限制，实际性能往往并不稳定。

综上，针对金属/CFRP 复合管的研究已经相对成熟，但对于其上开设诱导结构的相关研究尚不完善，且大多数研究集中于诱导孔。通常诱导结构是在适当位置去除部分材料，利用结构局部刚度降低，从而使变形时的峰值力随之降低。此外，合理的诱导结构设计还应使薄壁结构发生渐进稳定的破坏模式，从而保证其耐撞性能稳定。然而，在复合结构中进行诱导孔设计，会导致结构在该处产生不规则的变形模式，难以进行控制与预测，且目前大多数学者研究工况较为单一，基于多角度压缩工况下的研究相对较少。因此，本文提出了较为稳定的诱导槽式复合管构型，并基于多角度压缩工况，对其进行参数化影响研究及多目标优化设计，以期获得可以兼顾低峰值力与高比吸能的诱导结构设计方案。

1 耐撞性指标

结构的耐撞性能可以通过几个评价指标进行评估，这些指标用于结构能量吸收的初始设计阶段。其中，包括总能量吸收Etotal、峰值压溃力（peak crushing force，PCF）。

1.1 总能量吸收Etotal

碰撞过程中的总能量吸收为力-位移曲线下的面积，即

式中：Δ为压缩位移；P为相应位移下的冲击反力。

1.2 峰值压溃力PCF

峰值压溃力PCF是表征吸能结构在冲击过程中的一个重要参数，定义为在结构密实前载荷-位移曲线上的最大反力。

1.3 比吸能（specific energy absorption，SEA）

一般将比吸能定义为：在冲击过程中结构的总能量吸收与结构质量之比，即

由于本文以汽车部件应用工况作为研究背景，以汽车吸能盒为例，其考察的冲击角度范围可以达到30°。因此，考虑冲击角度因素，提出综合吸能性SEAθ，其表达式为

表1 冲击角度和权重分配

2 有限元模型及其验证

2.1 有限元模型

利用HYPERMESH 软件，建立复合管有限元模型，复合管的截面形式如图1（a）所示。复合管高度为250 mm，管径为99.5 mm，外侧铝管厚度为2 mm，内侧CFRP 铺层数为15 层，每层厚度为0.1 mm。此外，在本研究中CFRP 管的铺层角度为±30°，其铺层示意图如图1（b）所示。

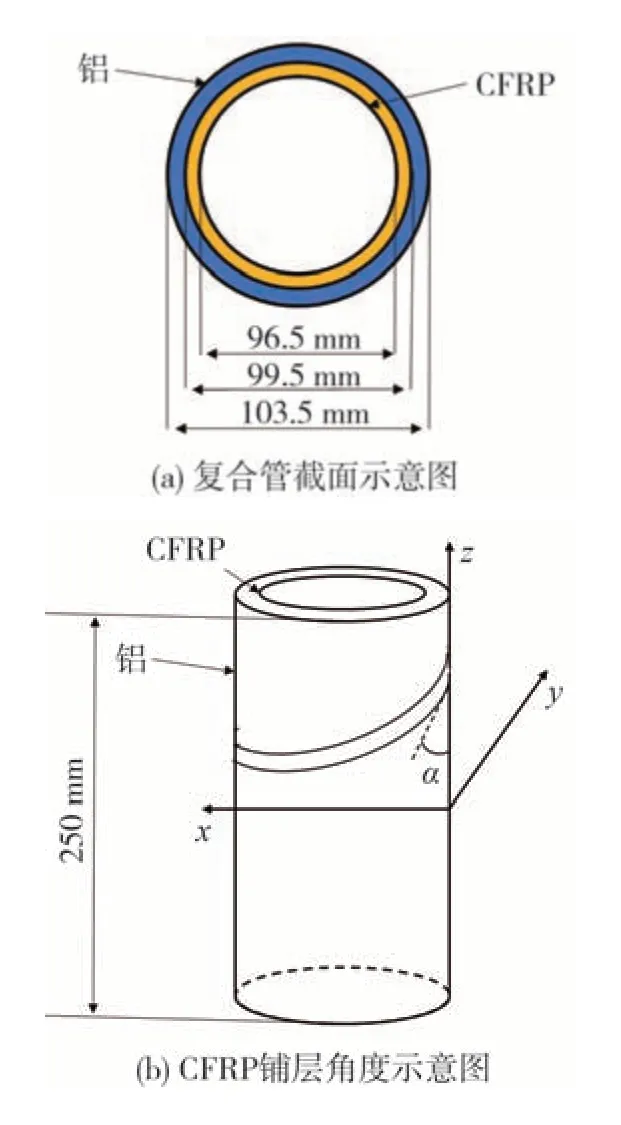
图1 铝/CFRP复合管结构构型

在平面外准静态多角度压缩加载条件下，复合管的有限元模型示意图如图2 所示。采用Belytschko-Tsay 四边形壳单元进行网格划分。为平衡计算效率和精度，进行了网格灵敏度分析，并对开诱导槽位置的网格进行了尺寸研究，最终确定诱导槽网格尺寸为1 mm，其余位置网格尺寸为2 mm。

图2 复合管有限元模型示意图

采用MAT_MODIFIED_PIECEWISE_LINEAR_PLASTICITY 材料模型来构建铝管模型，所选铝材型号为AA6063-T5，其塑性变形阶段应力应变值如表2 所示，材料属性如表3 所示；采用MAT_ENHANCED_COMPOSITE_DAMAGE 来构建CFRP铺层，所选CFRP型号为T300，材料属性如表4所示，并基于Chang-Chang 失效准则对复合材料的失效行为进行表征；采用MAT_RIGID对刚性墙进行建模。

表2 所选铝材塑性阶段应力应变值［26］

表3 所选铝材材料属性［26］

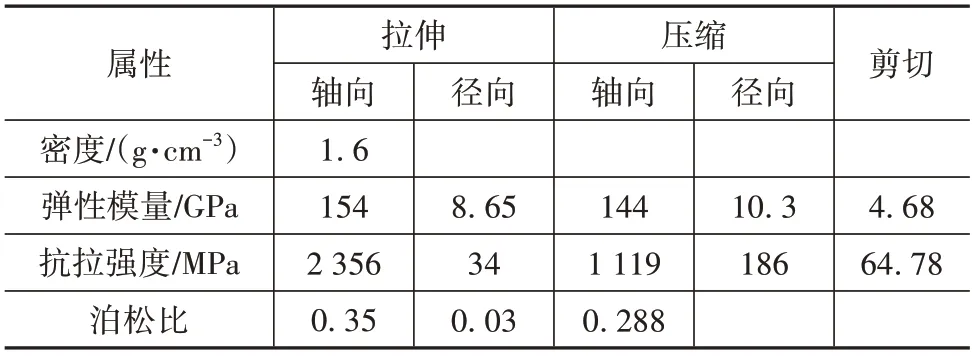
表4 所选CFRP材料属性［27］

采用CONTACT_AUTOMATIC_SINGLE_SURFACE 模拟复合管的自接触行为，采用CONTACT_AUTOMATIC_ONE_WAY_SURFACE_TO_SURFACE_TIEBREAK 模拟铝合金与CFRP 之间的连接，并用CONTACT_AUTOMATIC_SURFACE_TO_SURFACE模拟刚性墙与复合管之间的接触，其动态摩擦因数以及静态摩擦因数分别为0.2和0.3。

2.2 有限元模型的验证

为验证所采用有限元方法的准确性，建立与文献［13］中相同参数的铝合金包裹碳纤维复合管构型，进行了仿真试验验证，如图3 所示。由图可看出，曲线的幅值与趋势以及变形模式基本一致，有限元模型结果与文献［13］的试验结果吻合较好。对比试验与有限元模型的峰值力、吸能量及平均压溃力，如表5 所示，误差均在10%以内。相对于实际加工样件，有限元模型较为理想，不存在加工缺陷，所以其峰值力较高，且变形更加稳定，致使两者的曲线波动存在一定的差异性。综上，证实了本文有限元方法的合理性，可以用于后续的分析研究。

图3 仿真与试验的载荷-位移曲线与变形模式对比图

表5 有限元模型验证精度

3 结果与讨论

复合管具备优异的能量吸收能力，其在轴向下的变形模式也较为规则，但其具有较大的峰值力。在汽车结构安全设计中，薄壁结构的峰值载荷通常会有上限约束，不能超过后端结构的承载极限，否则会引起其他部件的破坏。因此，需要在复合管上进行合理的诱导设计，在保证其吸能性能的同时，降低其峰值载荷。

根据王凯等［28］的研究进行诱导孔的相关参数设置，开设诱导结构的复合管与无诱导结构的复合管具有相同的材料模型、边界条件以及接触定义，并根据网格灵敏度分析，将诱导槽以及诱导孔处的尺寸设置为1 mm，且其余设置参数均相同，有限元模型如图4所示。

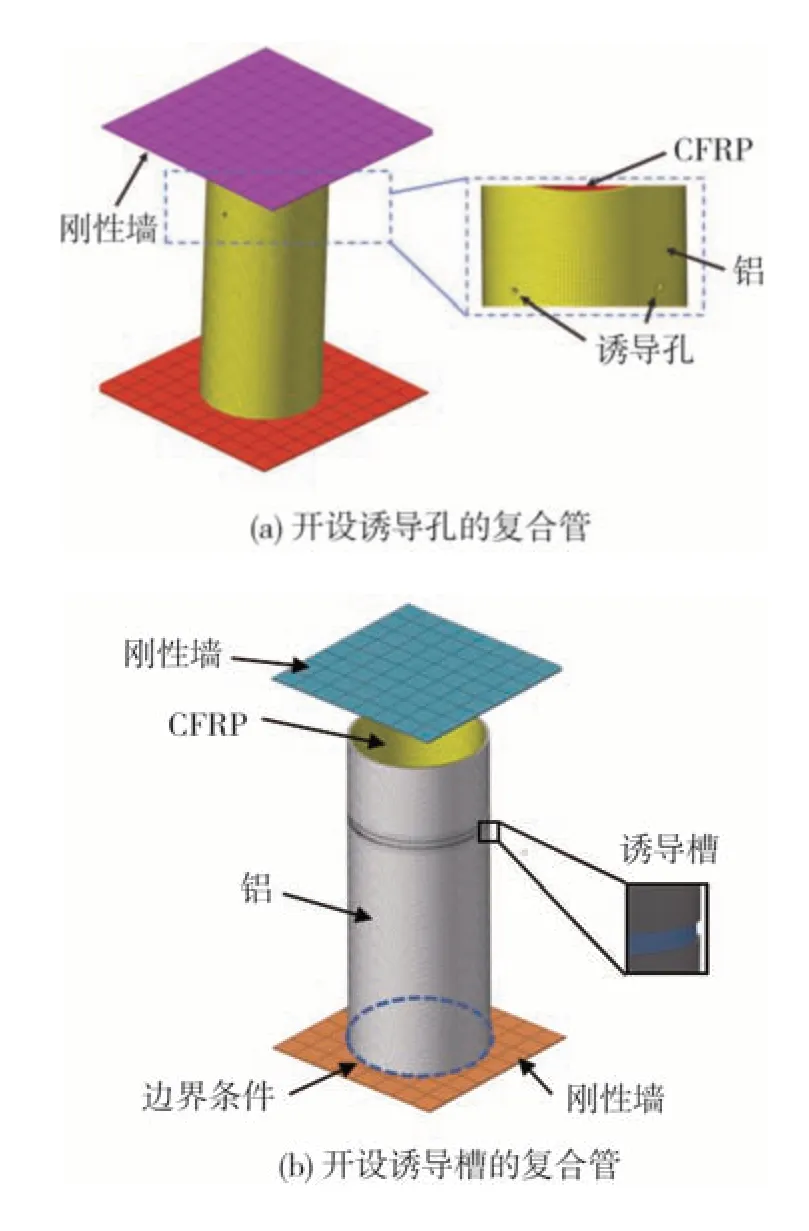
图4 具有不同诱导结构的复合管构型

通过对比图5 中开设诱导孔、开设诱导槽以及无诱导结构的复合管构型在多角度压缩下的比吸能以及全局峰值载荷（即轴向冲击下的峰值力）不难发现，相对于开设诱导孔，诱导槽可以在大幅降低初始峰值力的同时，保证比吸能的稳定。图6为3种模型在多角度压缩下的变形模式图。复合管上开设诱导结构，通过降低该处刚度从而诱导变形。然而，通过仿真结果对比发现，开设诱导孔的复合管随着加载角度的增大，变形不可控，甚至出现了整体弯曲，结构稳定性降低。而本文采取的诱导槽式复合管则在压缩密实前，始终保持稳定的渐进式压缩变形，从而保证了其吸能的稳定性。以上证实了诱导槽式复合管在兼顾低峰值力与高比吸能特性方面的应用潜力，接下来展开进一步的参数化研究，分析其主要影响因素。

图5 多角度工况下不同复合管结构的动力学响应

图6 无诱导结构与开设诱导结构的复合管变形模式图

3.1 诱导槽位置的影响

如图7 所示，本文将诱导槽参数分为连续参数与离散参数。其中，连续参数包括诱导槽位置与诱导槽尺寸；离散参数包括诱导槽形状与诱导槽数量。接下来将对上述参数对综合耐撞性能的影响机制展开分析。

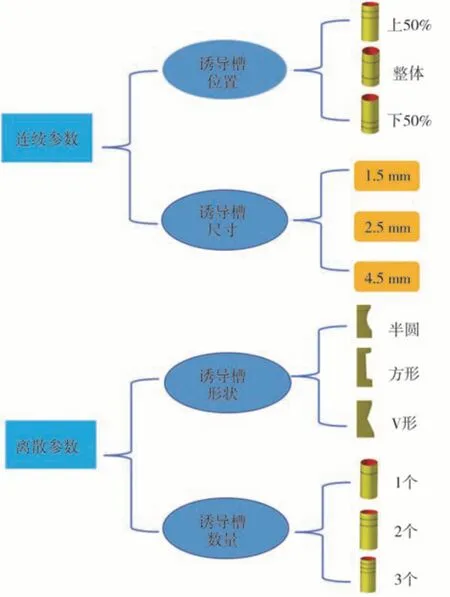
图7 诱导槽参数变化示意图

诱导槽开设的位置对于复合管的压缩变形模式具有较大影响，合理的开槽位置能够起到诱导变形的作用，反之将破坏其原有的变形模式。为研究诱导槽位置对复合管压缩变形模式及耐撞水平的影响，分别在复合管高度方向的上50%、下50%以及整体高度范围内开设大小为3.5 mm、内凹深度为1 mm的两个均匀分布的方形诱导槽结构。

图8 给出具有不同诱导槽位置的复合管在多角度工况下的变形模式。在轴向加载下，由于诱导槽的弱化效应，无论诱导槽分布在何处，所有复合管均首先在诱导槽位置产生变形。当诱导槽分布在上50%高度范围内时，在加载初期先于诱导槽处发生局部失稳变形，之后逐渐呈现渐进压溃变形。而其他两种诱导槽分布形式则存在较为明显的局部不规则变形。随着压缩角度的增加，诱导槽分布于上方的复合管的吸能优势越发明显，相比于另外两种构型产生的整体弯曲现象，它利用上方局部诱导槽，既削弱了轴向刚度去避免整体弯曲行为，同时保证了下方刚度实现较为稳定的渐进压溃模式。这也意味着，诱导槽不应开设于下50%的位置，否则在大角度工况下易诱发整体弯曲现象，严重削弱结构承载能力与吸能性能。

图8 具有不同诱导槽位置的复合管在多角度工况下的变形模式

进一步地，图9 给出不同诱导槽位置的复合管构型在准静态轴向压缩过程中的载荷-位移曲线，来重点考察对全局峰值力的影响效果。不难发现，所有复合管构型的峰值力都发生在初始阶段，且相对于无诱导结构的复合管具有基本相同的改善效果。结合上述对变形模式的分析，可以说明诱导槽的分布位置主要影响复合管结构的变形特征，对应于载荷-位移曲线在屈曲阶段应力波动的差异性。在压缩至诱导槽处时，不同构型的载荷均会形成波谷。不同的是，位于上方开设诱导槽的复合管在上部进行充分压缩后，进入了稳定的渐进压溃模式，其反力迅速恢复至较高水平，形成小范围波动，直至最终进入密实状态。而另外两种构型由于下部均开有诱导槽，导致整体结构在压缩过程中存在严重的失稳现象，载荷始终处于较低水平，不利于能量吸收。表6给出不同诱导槽分布位置的复合管在不同权重方案下的综合耐撞性能指标。可以直观地看到，诱导槽位置不同，复合管的全局峰值载荷基本不变，但是对综合比吸能指标影响很大。在上50%开设诱导槽的复合管构型在上文设定的3 种权重方案下均具有最优的性能表现，同时随着大角度工况权重的增加，其展示的性能优势更加明显。

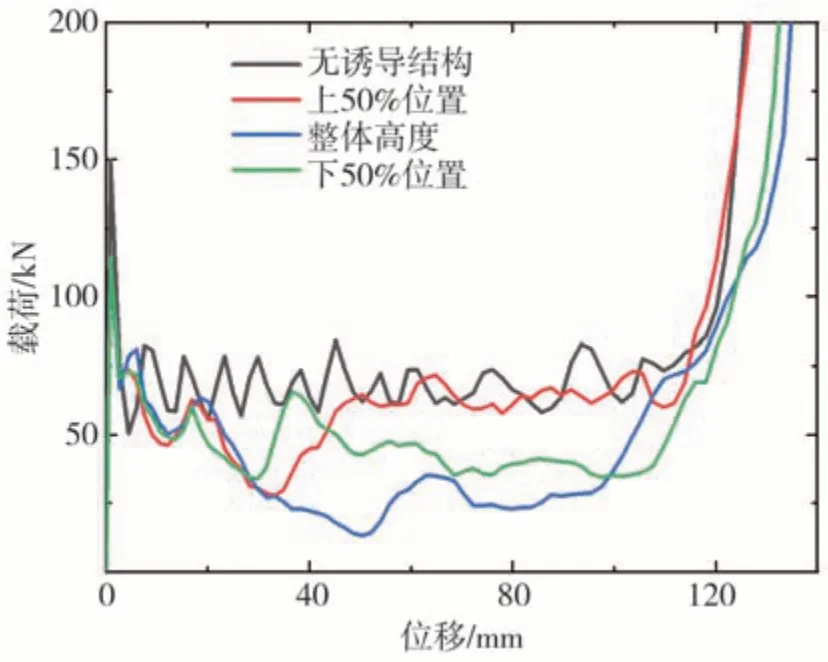
图9 不同诱导槽位置的复合管构型在准静态轴向压缩过程中的载荷-位移曲线

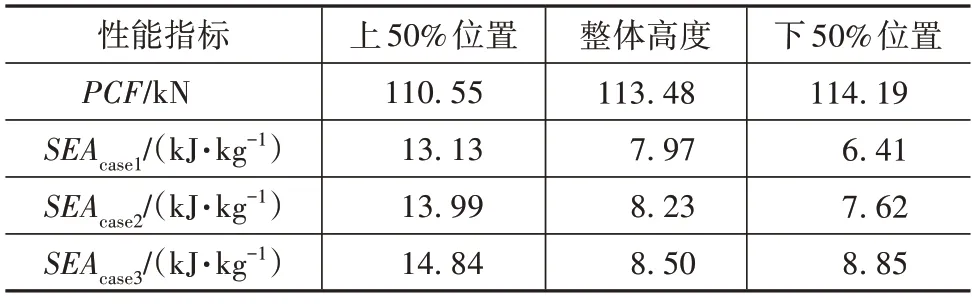
表6 不同诱导槽位置复合管综合耐撞性能指标

3.2 诱导槽数量的影响

基于上述对诱导槽位置的分析，进一步对上方开设诱导槽的数量进行影响研究。图10 给出不同诱导槽数量复合管构型的变形模式。首先可以看到，所有复合管构型均未发生整体弯曲现象，以此证实了上述对诱导槽位置的分析结论。同时，可以发现复合管会按照诱导槽分布的位置依次发生变形，从而对上部产生的变形折叠数量造成影响。进一步地，图11 给出不同诱导槽数量的复合管在轴向加载下的载荷-位移曲线，来重点考察对全局峰值力的影响效果。可以看出，诱导槽数量的变化并不影响全局峰值力发生的位置，对其改善效果的影响也相对较小，但是对屈曲阶段的应力波动具有明显影响。在上方开设一个诱导槽的复合管并未出现明显的波谷现象，而仅是体现在压缩初期的峰值降低，待诱导槽处压实后出现明显的第二峰值。而开设其他数量诱导槽的复合管则在压缩初期存在明显的应力波谷。表7 给出不同诱导槽数量的复合管综合耐撞性能指标。可以看到，随着诱导槽数量的增加，全局峰值力呈现先增大后减小的非单调变化规律。开设3个诱导槽的复合管具有最小的全局峰值力，而开设1 个诱导槽的复合管在各权重方案下的综合比吸能均为最大。考虑到加工的经济性与复杂性，选择1个诱导槽数量将是更为合理的。

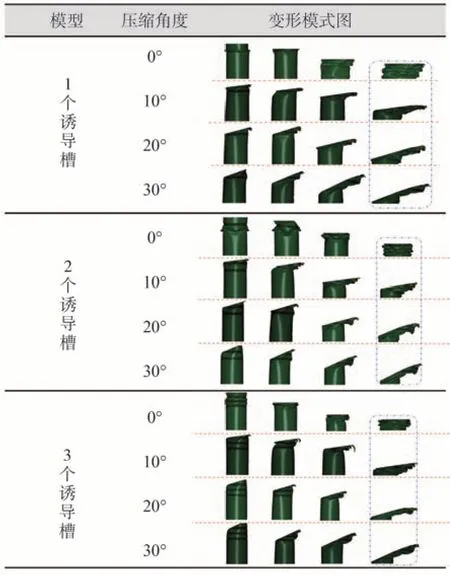
图10 不同诱导槽数量复合管构型的变形模式

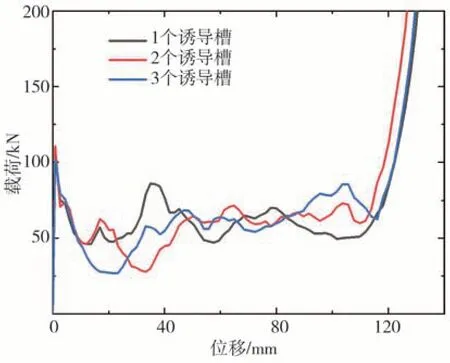
图11 不同诱导槽数量的复合管在轴向加载下的载荷-位移曲线

表7 不同诱导槽数量的复合管综合耐撞性能指标

3.3 诱导槽形状的影响

进一步针对诱导槽形状对综合耐撞性能的影响进行分析。在上述方形诱导槽的基础上，本文又引入两类常见的诱导槽形式，即半圆形与V 形，且保证其几何参数一致。

图12 给出不同诱导槽形状复合管在多角度工况下的变形模式。在小角度压缩时，不同形状诱导槽的复合管均以渐进压溃的方式进行变形吸能。随着角度增大至20°，在半圆形诱导槽的复合管底部，出现铝管与内侧CFRP 分离的现象，使两者耦合作用减弱，发生整体弯曲。当角度增至30°时，V 形诱导槽的复合管同样发生上述现象，以此证实了诱导槽形状主要对大角度工况下的变形模式具有重要影响，而对小角度工况影响较小。图13 给出不同诱导槽形状的复合管在轴向加载时的载荷-位移曲线，重点考察对全局峰值力的影响。可以看出，具有不同诱导槽形状的复合管最大峰值力仍发生在压缩初期，且所产生的初始峰值力具有较为显著的差异，而应力曲线整体波动形式趋于相同。表8 给出不同诱导槽形状复合管的综合耐撞性能指标。可以发现，半圆形诱导槽具有最小的全局峰值力，但是由于在不同压缩角度时，具有半圆形与V 形诱导槽形状的复合管均在大角度工况下存在整体弯曲的现象，使得它们在不同权重方案下的综合吸能指标均低于方形诱导槽。因此，将方形诱导槽作为本文后续优化研究的最佳诱导槽形状。

图12 不同诱导槽形状复合管在多角度工况下的变形模式

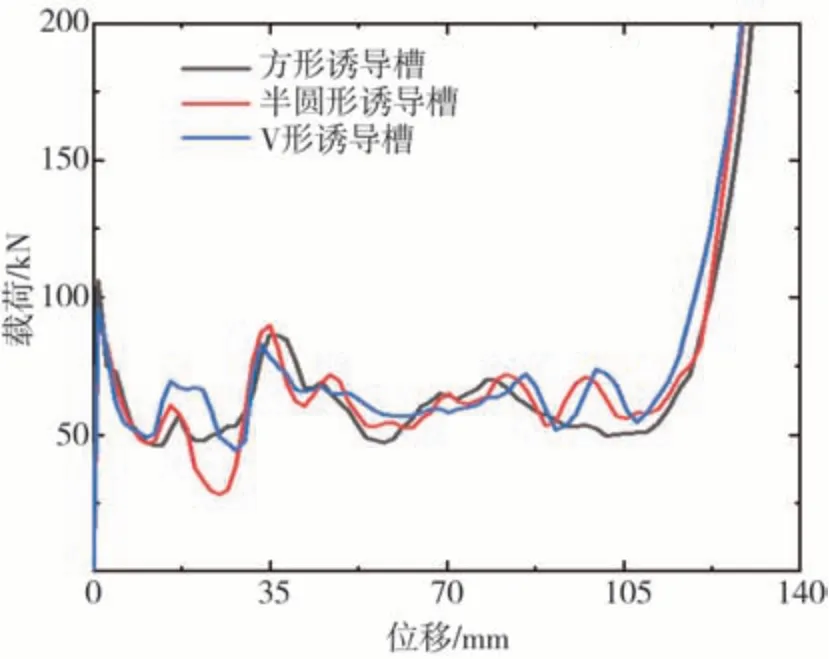
图13 不同诱导槽形状的复合管在轴向加载时的载荷-位移曲线

表8 不同诱导槽形状复合管的综合耐撞性能指标

3.4 诱导槽尺寸的影响

最后，文中对诱导槽尺寸对复合管结构在多角度工况下的耐撞性能进行分析。上述参数分析中，诱导槽尺寸均为 3.5 mm，本节设置了另外3 种诱导槽尺寸构型：1.5、2.5和4.5 mm。

图14 为不同诱导槽尺寸的复合管构型在多角度工况下的变形模式图。可以发现，在轴向加载下，不同诱导槽尺寸的复合管构型变形模式基本相同。当存在角度冲击时，在诱导槽尺寸过大或过小时，均会导致复合管在压缩后期诱发整体弯曲行为，造成结构利用率低下，导致吸能能力大幅衰减。因此，合理的诱导槽尺寸对于复合管的吸能稳定性具有重要作用。

图14 不同诱导槽尺寸的复合管构型在多角度工况下的变形模式图

图15 给出不同诱导槽尺寸复合管构型在轴向加载时的载荷-位移曲线，重点考察对全局峰值力的影响。可以发现，诱导槽的尺寸并不影响最大峰值力出现的位置，且第二峰值位置和幅值也基本相同，除诱导槽尺寸过大时出现了第二峰值滞后现象。随着诱导槽尺寸的增加，全局峰值力随之升高，但增长幅度相对较小。表9 给出不同诱导槽尺寸复合管的综合性能指标值。不难发现：由于诱导槽较小时不足以通过诱导作用避免整体弯曲行为的发生，导致了综合吸能量较低；而诱导槽尺寸较大时，会出现诱导过度现象，削弱复合管轴向刚度的同时，加深了对诱导槽局部位置变形程度的影响，进而诱发底端的整体弯曲行为。因此，诱导槽的尺寸应存在一个合理的设置区间。

图15 不同诱导槽尺寸复合管构型在轴向加载时的载荷-位移曲线

表9 不同诱导槽尺寸复合管的综合耐撞性能指标

4 多目标优化

上述参数研究中，关于诱导槽的形状与数量均为离散变量，通过对多角度工况下的综合耐撞性能分析，确定为在复合管上方开设一个方形诱导槽时，有利于吸能稳定性与制造经济性。而关于位置以及尺寸参数则属于连续变量，并已证实存在一个合理的设置区间，以期获得更好的综合耐撞性能，兼顾全局峰值力与综合吸能性。基于此，文中对位置参数以及尺寸参数开展多目标优化设计研究。

首先，对诱导槽的位置进行表征，将诱导槽的水平对称线距离壳体顶端水平面的高度设为d，当确定d时，即可获得诱导槽的具体分布位置。将d进行设计变量约束，即0 ＜d＜125 mm。同时，对诱导槽的尺寸h进行设计变量约束，即 1.5 mm＜h＜3.5 mm。在优化目标方面，把全局峰值力PCF以及综合比吸能SEAθ作为优化目标。多目标优化模型可以表示如下：

4.1 样本点筛选

考虑到变量个数以及计算成本，采用最优拉丁超立方方法进行15组样本点的筛选，并采用前12组用于构建代理模型，后3 组用于验证模型精度。表10给出不同样本点及其对应的目标性能值。

表10 不同样本点及其对应的目标性能值

4.2 代理模型的构建

基于前12 组样本点，采用响应面法对代理模型进行构建。考虑到代理模型拟合精度和鲁棒性，最终采用4阶多项式进行拟合。

其中，全局峰值力的代理模型如式（6）所示，各加权比重下的综合比吸能代理模型如式（7）～式（9）所示。

进一步地，采用误差平方值R2和均方根误差RMSE来评估响应面模型的精度，可通过以下公式进行计算：

式中：yi和分别为采样点i时的目标值以及所有样本点的计算平均值为根据代理模型预测的采样点i的目标计算值；n为采样点总数。如表11 所示，可以证实响应面模型的精度可以接受，以保证后续优化结果的准确性和有效性。

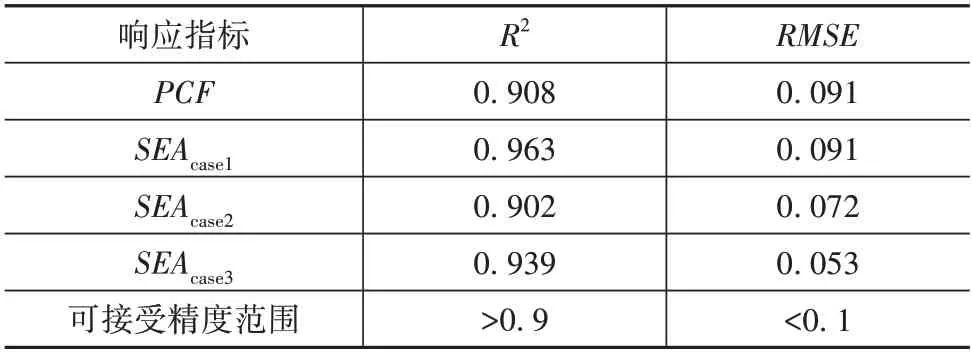
表11 响应面精度评价指标

进一步采用后3 组样本点对上述5 个代理模型进行精度验证，如表12 所示。不难发现，该方法构建的模型精度更高，最大误差小于10%。因此认为代理模型具有可信的精度，可以用于后续的多目标优化设计。

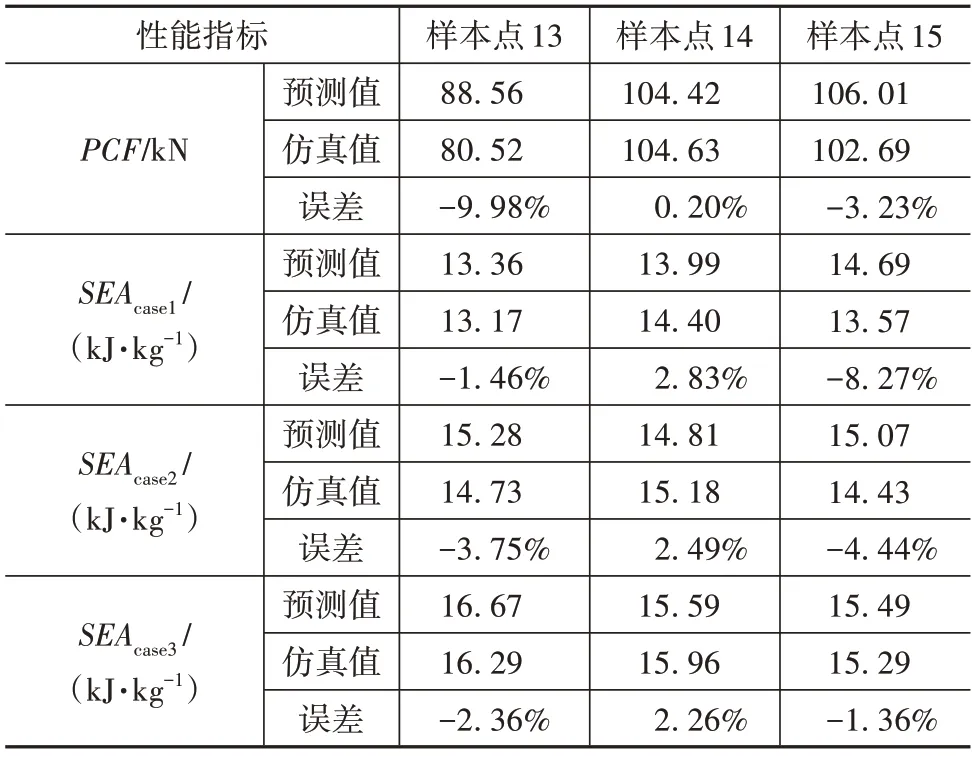
表12 代理模型耐撞性指标精度验证

4.3 多目标优化设计

针对问题的复杂程度与工程特点，采用NSGAII 算法进行优化，考虑到优化结果的稳定性与计算效率，算法参数设置如表13 所示。通过优化迭代得到Pareto解集，如图16所示，把最大综合吸能性作为主要考虑项，获得最终的优化解，即h=9.45 mm，d=1.54 mm。

图16 Pareto解集与最优解

表13 算法参数设置

为验证优化结果的准确性，对优化解的设计值进行仿真计算，结果如表14 所示，其与预测值的误差均在10%范围内，因此认为优化值有效。对优化前后的性能改进效果进行对比，如表15 所示。可以看到：优化后的结果在保证各工况权重方案的综合吸能性不降低的前提下，使全局峰值力下降35.52%，改善效果明显，更好地兼顾了低峰值力与高比吸能特性。

表14 最优解的预测精度验证

表15 优化前后复合管耐撞性指标

5 结论

基于铝/CFRP 复合管引入了诱导槽结构，并与无诱导结构以及开设诱导孔的复合管进行综合耐撞性能对比，并对其进行了主要参数影响分析及多目标优化设计研究，得到主要结论如下。

（1）通过对比开设诱导槽以及诱导孔两种诱导形式不难发现：当两者几何、材料等参数相同时，在轴向加载下，开设诱导孔对初始峰值力降低幅度较小；在多角度工况下，这种情况更加明显。此外，随着角度的进一步增大，易诱发局部的不规则变形，进而导致发生整体弯曲现象。而诱导槽式复合管构型则在大幅降低峰值力的同时，在各角度工况下均发生渐进压溃变形，保证了吸能的稳定性。

（2）诱导槽位置对于复合管的稳定变形起着主导性的作用；诱导槽的形状对于全局峰值力的降低具有明显效果。结合综合耐撞性能与加工经济性，选择在复合管高度方向的上50%范围内开设一个矩形诱导槽，可以大幅降低峰值力水平，同时兼顾吸能稳定性。

（3）通过多目标优化设计，寻找诱导槽尺寸与诱导槽位置的最佳参数组合，相比于无诱导结构的复合管，优化方案的诱导槽构型既削弱了轴向刚度，降低了轴向加载下产生的全局峰值力，同时在大角度工况下，起到了诱导结构发生稳定变形的作用，以确保综合耐撞性能始终处于较高水平。