基于对偶性原理的配电变压器高频电磁暂态模型

杨庆，崔浩楠，揭青松，刘红文，黄继盛

（1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400030；2.云南电网有限责任公司电力科学研究院，云南 昆明 650217；3.云南电网有限责任公司临沧供电局，云南 临沧 677000）

0 前言

随着智能电网的全面建设，物联网技术在各业务环节得到广泛应用。电力物联网包括感知层、网络层和应用层，其中感知层实现电力生产各环节传感数据的统一感知与表达，建立统一信息模型，规范感知层的数据接入[1]。网络层按照规范化的统一通信规约实现对数据的传送。配电网故障行波信号频谱主要分布在10 kHz～100 kHz，适用于输电线路的单端定位方法难以用于复杂的配电线路，只能通过多端测量来实现故障定位。虽然在台区等配变处架设了互感器，但其主要是用于电压电流测量，频带较窄，并不适用于故障暂态信号的直接获取，通常在配电变压器二次侧感知故障暂态信号实现多端测量故障定位[2-3]。电力线通信(power line communication ,PLC) 技术使用现有电力线进行数据传输，为智能电网应用可用的通信解决方案之一[4-6]。在窄带(Narrow-Band,NB)通信技术的应用中，在美国、日本和中国等国家频率使用范围从3 kHz 到500 kHz。然而在配电网中，配电变压器作为中压网和低压网之间的物理连接，是用于传输电能，在设计时并未考虑传输高频信号，对高频信号传输衰减较大[7]。因此，研究变压器的高频模型，对于获取故障行波信号、PLC 信号在配电变压器中的传播特性和中压、低压电力线通信信道建模具有重要的理论意义和工程应用价值，对智能电网的感知层和网络层建设具有参考价值。

配电变压器高频模型的研究可以分为两类：集总参数模型和黑盒模型。集总参数模型由一个集总电路使用电阻、电感和电容来模拟变压器在频域下的阻抗特性。这些模型通常是基于低频模型，同时结合了由变压器端口测量到的高频现象[8-12]。Tran-Anh 等人通过从低压侧测量任意端口的短路开路阻抗特性，发现在高于一定频率后，端口开路短路阻抗特性重合，由此提出中频(MF) 模型和高频(HF) 模型，中频从低压侧对变压器进行建模，相当于将高压侧参数全部等效至低压侧，高压侧不应有任何参数，但提出的模型中仍重复考虑了高压侧对地电容的影响。除此外，基于中频模型提出高频模型时，忽略了铁芯的影响，理由是高频下从低压侧测得的开路短路端口特性相同，变压器不起作用，而实际原因是高压侧相间杂散电容在高频下呈低阻态，虽去掉理想变压器后对低压侧端口特性无影响，对高压侧端口特性的影响较大，作者并未验证变压器模型在高压侧的适用性[9]。Cataliotti 利用已提出的HF 模型，测量了不同容量油浸式变压器的在50kHz～150 kHz 下模型参数[10]。Lefort 在高压侧建立模型，通过测量端口阻抗特性后使用集总参数等效，对于阻抗特性中存在的谐振点，可选择在低压侧串联一个并联谐振电路来代表，建立的模型三相励磁参数相同，而实际上由于中间相磁路短于边上两相，中间相励磁电感应大于其余两相，同时对于高压侧相间电容并没有好的测量方法[11]。黑箱模型是根据配电变压器在这些终端上的行为对其进行建模的。在这种情况下，不需要知道它的物理特性[13-18]。Gustavsen B 以导纳矩阵为基础，建立了变压器各端子电压和电流之间的关系[13]，利用此方法还测量了Yy 和Dy 接法变压器的传输特性[14]。同时基于原有测量方法的基础上，增加了开路测量，使用混合方法计算导纳矩阵，提高了精度[15]。考虑到测量工具的昂贵，后续研究中还使用了低廉的FRA 工具，间接测得导纳矩阵参数[17]。Sathler 测量了单相配电变压器导纳矩阵，建立了变压器在窄带下用于研究PLC 信号传输的宽频模型[6]。现有的集总参数模型多为使用三个参数相同单相变压器按相应联结方式联结来等效三相变压器，而实际由于磁路的长度不一致会导致各相激磁参数不同[19]。同时在给出模型时并未提出相应理论来进行模型推导，导致模型中参数重复。此外，在验证模型有效性过程中，多为在频域上验证，而在时域上验证较少。而黑箱方法一般精确性高，但参数无特定物理意义。同时两种方法中多为研究建模方法对于单类型变压器适用性，未将模型应用于不同类型配电变压器。

从两种模型的物理意义来看，集总参数模型的参数具有明显对应的物理意义的优势，因此本文根据低频暂态下基于对偶性原理的变压器模型进行修正后提出配电变压器的高频模型，详细阐述了高频模型的推导过程，避免了像以往高频模型中杂散电容的重复测量。考虑到各相励磁的不同与相同之处，通过两次测量分别计算出各相励磁参数大小。将模型应用于不同类型变压器上，测量并计算了两种类型配电变压器参数。在得到参数后搭建仿真模型，同时在现场搭建试验平台进行实验，对比验证了模型在频域和时域上的有效性。

1 变压器高频模型及参数提取方法

1.1 基于对偶性原理的变压器低频电磁暂态模型

电路与磁路的对偶关系可简单归纳为：磁路中磁动势和磁阻分别对应电路中电流源和电感，磁路网孔和节点分别对应电路节点和网孔[20]。

配电变压器为三相三柱芯式变压器[21]，物理结构图如图1(a) 所示，高压侧线圈HV 在芯柱的外侧，低压侧线圈LV 在内侧，其中实线表示变压器铁芯内主磁通，虚线表示漏磁通，ΦLC表示铁芯与低压绕组间的漏磁通，ΦHL表示低压绕组与高压绕组间的漏磁通，Φ0表示铁芯与绕组外侧空气间漏磁通[22]。

图1 变压器物理结构

与图1(a) 对应的三相三柱变压器等值磁通如图1(b) 所示，FL和FH分别为低压绕组与高压绕组对应的磁动势，其中Rm、Ry分别为中心柱和铁轭对应的磁阻。RLC为铁芯与低压绕组间漏磁通对应的磁阻，RHL为低压绕组与高压绕组间漏磁通对应的磁阻，R0为铁芯与空气间漏磁通对应的磁阻。

以中心柱磁支路为例，FL和FH经对偶变换后成为相应的电流源，Rm经过对偶变化后得到ZL，磁阻RHL和R0经过对偶变化后得到电感L3和L0，同理, 磁路中的其他部分可以通过相似的对偶变换规则得到相应的等效电路。将电流源等效替换为变压器，增加相应绕组电阻。考虑到杂散电容影响，连接组别为Dy 接法，得到的模型如图1(c)所示[23]。

1.2 变压器高频模型及参数提取

在高频情况，图2 所示的低频电磁暂态模型不能直接应用，主要是此模型用于低频电磁暂态时需考虑变压器线圈的饱和效应，将线圈电感视为非线性。但在高频情况下，故障暂态信号和用于PLC 传输的信号幅值有限，不会导致配电变压器磁饱和，可将电感视为线性。因此，可以通过对基于对偶性原理的变压器低频模型进行修正而解决上述问题。

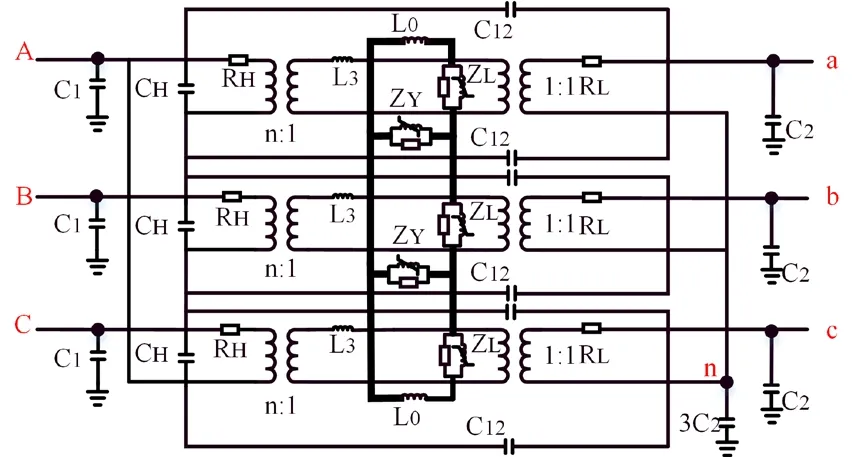
图2 变压器物理结构及对应电路模型

考虑到Dy 接法的配电变压器零序电感远小于Yy 接法，高频模型中忽略零序电感L0[24-25]。各相高压侧杂散电容C1呈Y 型接法，可变换为三角接法，而相间杂散电容CH同为三角接法，并联后可合并为相间杂散电容CH1。低频下，漏感L3远小于杂散电容阻抗CH1，略去后将图2模型中的ZL和ZY并联后和高压侧绕组间杂散电容CH1组成的并联谐振电路等效至低压侧。高频下，泄漏阻抗随频率增加，而杂散电容阻抗减小，相当于高压侧短路。将图2 中的泄漏阻抗等效至低压侧可得到如图3 所示的高频模型中的泄漏阻抗RL 电路。

图3 本文变压器高频模型

图3 其中漏阻抗和励磁阻抗部分电感可能和内部杂散电容产生谐振，并不是完全为单一RLC 谐振电路或是RL 电路，可分别用Za、Zb、Zc和Z1来替代。最终模型由三相励磁相互关联的励磁阻抗Za、Zb、Zc、漏阻抗Z1、高低压侧电容C12及低压侧对地电容C2、变比为n的理想变压器组成。模型中，由于变压器两侧对称，a,c 两相对应的磁化阻抗Za，Zc相同。同时，磁路不对称会影响励磁，中间相磁路短于其他两相，Zb谐振电路中电感Lb较大。各相漏阻抗Z1相同。

可以看出，以上的电磁暂态模型符合高频情况下的物理过程。对实际变压器，通过外界激励或阻抗分析仪在外部进行测试，无需对其内部特性进行测量，便可建立起其对应的高频电磁暂态模型：分别在高压侧开路短路状态下测量a-n 的幅频特性，开路时幅频特性由Z1和Za//Zb+Zc串联决定，而短路时由Z1决定。Za//Zb+Zc在高频下呈低阻抗，则在高频下高压侧开路短路下a-n 的阻抗特性重合，和以往文献测量结果符合[8]。由短路实验求出Z1，开路实验求出Za、Zb、Zc。分别得到漏阻抗，激磁阻抗和杂散电容幅频特性后，使用集总参数元件来代替[26]。

2 参数测量计算

为验证变压器高频模型的正确性，本文选取了两种典型的Dyn11 接法配电变压器(10/0.4)，分别是油浸式(T1/400 kVA)和干式配电变压器(T2/315 kVA)。如图4 利用阻抗分析仪WK6500B 对集总参数模型参数开展测量，测量频率范围为100 Hz～1 MHz。

图4 变压器参数测量

测试用导线在测试时相当于和被测元件串联，在高频时影响不可忽略。将导线短接后可得到其阻抗特性，可等效为0.1 W 电阻与8.8 μH电感串联。

2.1 泄漏阻抗测量计算

测量漏阻抗的连线如图5 所示，通过将高压侧端口短路，在低压侧测量一个端口的阻抗特性可以得到泄漏阻抗参数，即模型中的Z1。

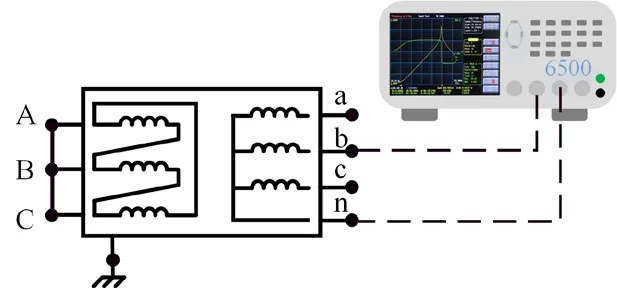
图5 漏阻抗测量

图6 (a)和图6(b)分别为油浸式变压器(T1)和干式变压器(T2)测得的漏阻抗特性，在大部分频率下可看作线性，可以使用RL 电路来等效。但油浸式变压器在40 kHz 时存在一个谐振点，需要额外串联一个RLC 并联谐振电路来等效[27]。

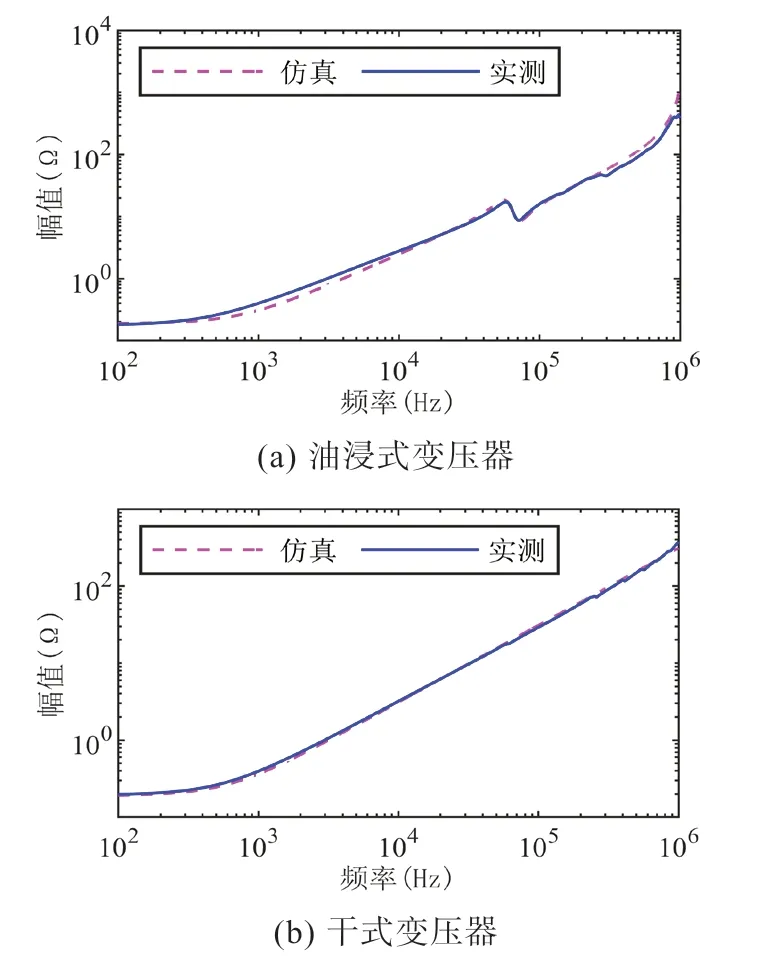
图6 两种变压器的漏阻抗特性

对于油浸式变压器，RLC 并联谐振电路中的Rl，Ll，Cl的值可以由下式得到：

其中，ωl=2πfl，ωl为谐振点角频率，Ql为品质因数，由式可以计算得到。

fl1和fl2为谐振点阻抗衰减-3dB 对应的频率。同时，R、串联电路中的LL、RL可以计算为：

其中，fm为测量序列中的最小频率。

另一方面，对于干式变压器：

计算结果如表1 所示。由计算结果得出的参数的阻抗特性如图6 虚线所示。

表1 两种变压器漏阻抗参数

2.2 磁化阻抗测量计算

由于三相三柱式变压器中间相磁路短于其他相，相应的电感大。三相参数不相同，因此需要多次测试来得到各自参数。

2.2.1 a,c相磁化阻抗Za，Zc测量计算

图7(a) 为测量电路连线，通过将低压侧中间相短路，测量a-n 阻抗特性，对应的等效电路如图7(b)。由于低频下Zl远远小于磁化阻抗，可忽略。低频下(＜10 kHz)测试所得阻抗为磁化阻抗，可看作Za和Zc并联，即2 个Za并联。

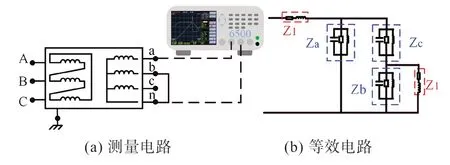
图7 a,c相磁化阻抗测量

图8 为两种变压器a-n 在b 相短路情况下的阻抗特性，可由并联谐振电路R1、L1、C1等效。通过式（5），可以得到a,c 相磁化阻抗参数为：

图8 两种变压器a-n（b相短路）阻抗特性

而干式变压器在100 kHz 处存在一个谐振点，这是由磁化阻抗造成的，需要再串联一个R11、L11、C11并联谐振。

2.2.2 b相磁化阻抗Zb测量计算

测量电路如图9(a) 所示，使用阻抗分析仪直接在配电变压器低压侧测量b-n 阻抗特性。图9(b)为等效电路，可以看出测得的阻抗可以看作中间柱磁化阻抗和其余两柱磁化阻抗之和的并联。

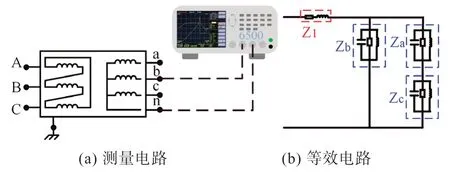
图9 b相磁化阻抗测量

两种变压器测量结果如图10 所示，可由并联谐振电路R2、L2、C2等效。同时根据等效电路图可得：

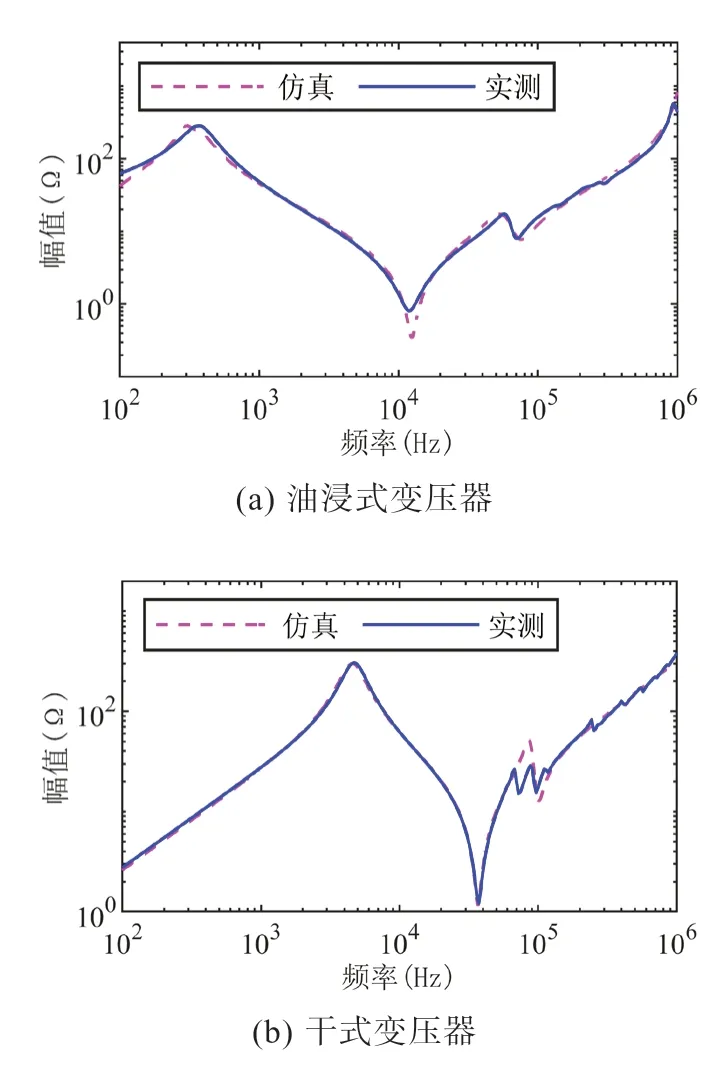
图10 两种变压器b-n阻抗特性

通过计算，可以得到中间柱上激磁阻抗参数为：

计算结果如表2 所示，由计算得出的电路低频下阻抗特性为图8，10 虚线所示，和实测数据相符，说明计算得到的参数准确无误。中间柱对应的磁化阻抗中的电感大于两侧磁化阻抗中的电感，与前文分析结果对应。

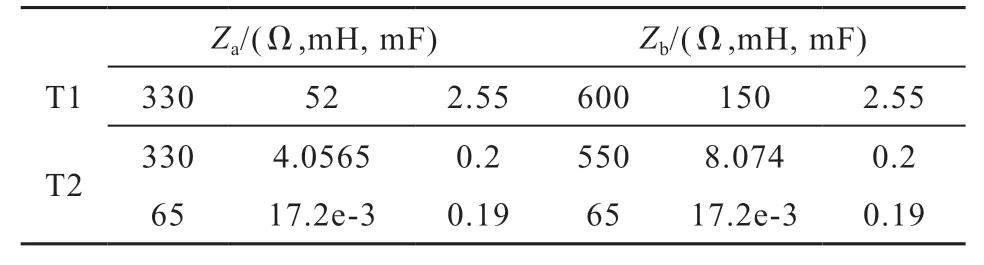
表2 两种变压器磁化阻抗参数

2.2.3 杂散电容测量计算

杂散电容测量可由三次实验得到，按照如图11 所示电路连接后，可得到三组电容参数Cap1，Cap2，Cap3。其值可由下式得到：

图11 杂散电容测量

其中，Zci为每次电容测量的阻抗。

通过模型的电路连接可知，电容参数C1，C2，C12和Cap1，Cap2，Cap3关系如式（10），其值可由Cap1，Cap2，Cap3计算得到。

计算结果如表3 所示，可以看出，干式变压器的杂散电容远小于油浸式变压器，同时相较于相间电容，低压侧对地电容较大。

表3 两种变压器杂散电容参数

3 变压器高频模型频域验证

为验证本文提出的模型的有效性，首先在频域下进行了实验验证。在频域下进行模型准确性验证是通过比较高频模型在PSCAD 软件中端口阻抗特性和阻抗分析仪测量的阻抗特性得到。

3.1 低压侧验证

在低压侧分别使用阻抗分析仪对两种变压器a-n，a-n(c 相短路) 和a-n(b,c 相短路) 在高压侧开路情况下进行了端口特性测量。其中，各相的短路是使用导线分别将对应相和中性点连接起来。

图12(a)，(b)，(c) 实线分别为油浸式变压器(T1) 的a-n 在无短路，c 相短路，b,c 相同时短路情况下的阻抗特性，虚线为仿真软件搭建的变压器模型得到的对应情况下的阻抗特性。仿真和实测数据在高频下(＞1 kHz)基本一致，仅在低频下(＜1 kHz)端口特性有些许偏差。其中，图12(b)中除了磁化阻抗和漏阻抗造成的震荡，在13 kHz 处也存在一个震荡，这是由于c相短路后，c 相漏阻抗的电感和c 相磁化阻抗中的电容谐振造成的。同理，将b,c 两相短路后，图12(c)在8.7 kHz 处也存在一个震荡，这是由于b,c 相短路后，b,c 相漏阻抗的电感和a,b,c 相磁化阻抗中的电容谐振造成的。

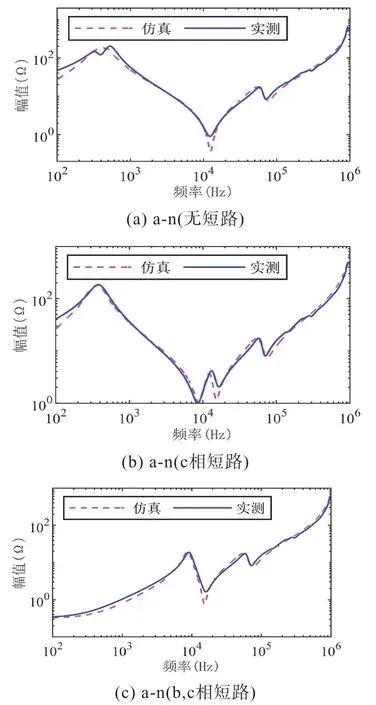
图12 油浸式变压器a-n在不同短路情况下的阻抗特性

图13 为干式变压器(T2)在低压侧不同短路情况下仿真阻抗特性和实测阻抗特性。由图可以看出，a-n 在其他端口不同短路情况下仿真得到的阻抗特性和实测阻抗特性几乎重合，只在高频情况下一些小的谐振点不能达到完全符合。相较于油浸式变压器，干式变压器在频域下的实测阻抗特性和仿真结果更加匹配。同样地，当存在其他相短路时，a-n 阻抗特性也产生了不同于无短路时的谐振点。

图13 干式变压器a-n在不同短路情况下的阻抗特性

3.2 高压侧验证

图14(a)和14(b)分别为油浸式(T1)和干式变压器(T2)在低压侧短路情况下的阻抗特性。可以看出，仿真得到的高压侧阻抗特性和实测高压侧阻抗特性基本符合。其中，油浸式变压器实测和仿真在谐振峰值上存在微小差异，其余部分相符。干式变压器的高压侧阻抗在低频下相符，在(＞20 kHz)存在一定震荡，但趋势和峰值大小相同。因此，通过在低压侧高压侧分别仿真变压器模型端口特性和实测特性对比，可以说明变压器模型在频域下有效。

图14 两种变压器高压侧阻抗特性

4 变压器高频模型时域验证

为研究配电变压器在时域下的传输特性，搭建了实验电路并与在PSCAD 下的时域仿真进行比较。实验电路由一个任意波形发生器(Tektronix AFG3011)作为信号源，一个示波器(Tektronix TDS 2024C)采集信号，时域测量实验的实物图如图15 所示。

图15 时域测量实验

如图16 所示，高压侧1，2，3 点接入电阻接地，低压侧非注入相接电阻接地。390 Ω 为线路特征阻抗[28]，50 Ω 为低压侧线路特征阻抗。在4 点使用函数发生器激励一个方波脉冲信号，大小为10 V，进行两次测试，所用脉冲信号持续时间分别为5 μs 和10 μs。同时在高压侧1，2，3 点和注入点4 分别采集信号。

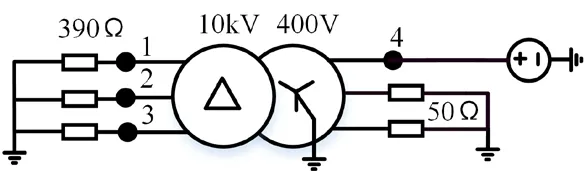
图16 时域测量电路

4.1 油浸式变压器高频模型时域验证

图17 ，18 为激励信号为5 μs 和10 μs 时的输入输出实测和仿真波形图。其中，a,b,c,d 分别代表端口4，1，2，3 的信号。紫色虚线为使用变压器集总参数模型得到的仿真信号，蓝色虚线为实测信号。

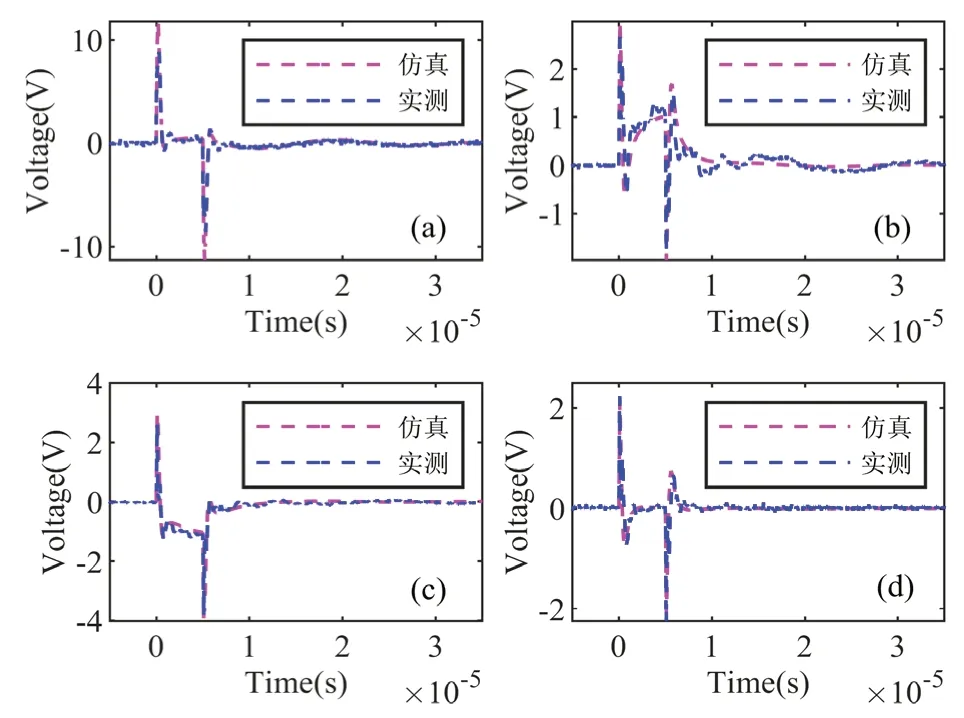
图17 油浸式变压器时域测量实验（脉宽=5 μs）

图18 油浸式变压器时域测量实验（脉宽=10 μs）

图17 (b)，(c)，(d) 为分别为高压侧A,B,C相输出信号，每个信号都存在尖峰，这是由于变压器高压侧绕组间杂散电容造成的。当方波脉冲信号作用于变压器上时，杂散电容C12上电压为0，不能突变。此时1，2，3 端口处电压大小为负载390 Ω 和电源内阻的分压，初始值很大，随着电容的充电而逐渐减小。5 μs 时下降沿造成的尖峰同理，因此输出信号存在两个尖峰。两次实验输入信号脉宽的不同只影响输出信号脉宽，而存在的尖峰和大小几乎不影响。图19 为激励信号脉宽为5 μs 时的输入输出实测和仿真波形图，可以看出仿真和实测波形一致。图20 为激励信号脉宽为10 μs 时的输入输出实测和仿真波形图，其中1 端口实测信号存在震荡，和仿真结果近似相符，其余端口幅值和形状相同。

图20 干式变压器时域测量实验（脉宽=10 μs）

4.2 干式变压器高频模型时域验证

和油浸式变压器得到的结果相似，两次实验输入信号脉宽的不同只影响输出信号脉宽，而存在的尖峰和大小几乎不影响。与油浸式变压器相比，油浸式变压器在时域下的实测阻抗特性和仿真结果更加一致。通过在两种变压器不同脉宽信号注入实验，仿真数据和实测数据在时域上较为符合，可以说明本变压器模型在时域下有效。

5 结束语

本文以低频电磁暂态下的变压器模型为基础，提出了配电变压器高频模型，根据变压器存在的对称关系，进行多次测量得到了变压器高频模型的各相参数。通过在PSCAD 软件中搭建的暂态模型电路，并与现场相同电路下的实验数据进行对比，验证了变压器模型对两种不同类型变压器在时域和频域下的有效性。在频域验证下，较于油浸式变压器，干式变压器在频域下的仿真阻抗特性和实测数据更加符合。导致此情况产生的原因可能是干式变压器的励磁阻抗远小于油浸式变压器，线圈的非线性特性对干式变压器励磁影响较小。从时域分析结果可以得到，油浸式变压器仿真端口信号的大小和形状和实测数据更加符合。