基于深度学习网络的机器人定位误差估计与补偿研究

田立国，熊 磊

（汉中职业技术学院 汽车与机电工程学院，汉中 723000）

智能机器人的应用范围日益扩大，对机器人定位的准确性提出了更高的要求[1-3]。在实际工作中，机器人通常会处于持续运转的状态，这样便会出现关节磨损、连杆变形、电机发热、负载量大等问题，造成其末端期望与实际位姿的偏离，产生一定的定位误差[4-6]。因此，为了使机器人能够高效、平稳地完成既定工作任务，对其定位误差进行估计与补偿非常必要。

近年来，有学者通过立方体网格建立以角度与距离为偏差的误差传输函数，根据该函数提出机器人定位误差补偿方法，对定位点每个方向的误差进行相应补偿[7]；有学者利用图卷积网络构建机器人定位误差预测模型，获取机器人定位误差，并将误差补偿问题转换成优化问题，利用遗传算法对优化问题进行求解，进而达到补偿误差的目的[8]。上述2种方法虽然对机器人定位误差起到了一定补偿作用，但是第一种方法通过空间网格法对机器人定位进行采样，缺少泛化能力，在实际工作中应用性不强；第二种方法则在构建机器人定位误差预测模型时，涉及大量的编码与解码操作，运算量较大，增加了算法的实现难度。

深度学习网络通常是指具有多个隐含层的神经网络，可以含有多个非线性变换，擅长对各种类型数据中的复杂模式进行识别，有着较强的模型拟合以及提取特征的能力[9-10]。因此本文提出基于深度学习网络的机器人定位误差估计与补偿方法，可以准确、合理地对机器人定位误差进行估计与补偿，具有较强的应用性。

1 机器人定位误差估计与补偿

1.1 机器人定位空间采样

由于机器人定位误差的初始状态，需要通过采样点数据才能反映出来，所以对机器人定位误差进行估计的前提，便是要选择适当的采样点。对于机器人定位误差而言，其采样点不仅要包括机器人整体位置移动的信息，还要包括其末端姿态的信息，这是因为当机器人到达某一目标位置时，其姿态也会产生不同的变化，进而会使机器人的有关关节角度发生改变，由此说明机器人定位误差与其整体移动位置和关节角度，也就是位姿有着较强的相关性。在工作空间内，为了使机器人定位误差得到准确估计与有效补偿，选择采样点时应注意要最大程度覆盖所有关节，以及采样点个数的设置要合理。为此本文使用拉丁超立方体采样（LHS）方法来规划机器人定位采样点。该方法通过分层随机抽样的方式，从变量分布区域进行快速采样，利用此方法可以在机器人工作间中得到适当的采样点集合。

设定采样变量维度用δ 描述，采样点个数用N描述，随机某个采样变量用sij（i=1，2，…，N；j=1，2，…，δ）描述，其分布函数用Aij描述，在区间（0，1）内生成的随机数用ζij描述，则采样变量sij为

如果机器人关节角度空间维度为l，把所有维度中的变量进行随机分布，产生数量是N 的采样点集合，那么关于s 的矩阵可以描述为

为了评估采样点在机器人工作空间里分布的均匀性，可以引进点集偏差理论。设定机器人工作空间Z 中，数量是N 的采样点用s′1，s′2，…，s′N描述，则第i 组采样点相应区间［0，si］中的体积函数F（si）可以描述为

设定s′1，s′2，…，s′N在Z 中的点集偏差用e 描述，存在于［0，si］中的采样点集合的个数用N（si）描述，当使用点集偏差理论评估采样点分布是否均匀时，e 越小，说明其相对应的点集分布越均匀，反之亦然。e 用公式描述为

利用抽样的方式产生多组采样点，再通过计算就可获取所有采样点的e 值，而最终使用的采样点则是e 值最小的那组点集，由此便得到维度为l 的机器人定位空间中的采样点。利用获取的采样点就可以对机器人定位误差进行估计与补偿。

1.2 机器人定位误差分析

机器人在工作时，通常情况下都会在其末端配置执行器，通过末端执行器来完成工作任务，因此对机器人末端的位姿进行分析非常重要。在笛卡尔空间内，设定机器人末端到达某个目标点的理论位姿坐标用Pt（xt，yt，zt）描述，实际位姿坐标P′（x′，y′，z′），那么在该目标点处的定位误差矢量E 可以描述为

机器人绝对定位误差通过欧氏距离可以描述为

1.3 基于GPSO-DNN 的机器人定位误差估计与补偿

1.3.1 GPSO-DNN 网络模型的构建

本文采用深度神经网络（DNN）模型对机器人定位误差进行估计。设定用于机器人定位误差估计的DNN 模型的输入量用［x1，x2，…，xn］描述，输出量用［y1，y2，…，ym］描述，二者分别为机器人末端理论位姿数据与机器人末端定位误差，而二者的维度决定了DNN 模型中输入与输出层中节点的数量。如果DNN 中共有L 个隐含层，那么位置是l 的隐含层的输出可以描述为

式中：wl为l 与l-1 层节点的连接权值矩阵，cl为阈值向量；μ（x）为ReLU 激活函数，可以描述为

在DNN 网络模型中，影响模型的机器人定位误差估计性能及估计结果较为重要的因素就是隐含层的层数与节点个数，本文使用经验法对DNN模型的隐含层最优节点个数范围进行确定，描述为

式中：DNN 模型内输入与输出两层内节点个数用n与m 描述，常数用σ∈［1，10］描述。

对于DNN 模型来说，初始化权值与阈值方法的好坏，直接关系其收敛速度的快慢。传统算法中通常采用随机的方式进行初始化操作，降低了DNN模型的收敛效率。所以本文通过粒子群算法（PSO）获取深度神经网络权值与阈值的最佳初始值，达到优化DNN 的目的。

（1）在PSO 算法的初始阶段，粒子呈随机分布的状态，这便导致部分粒子的适应度会产生较大误差，影响收敛速度。因此，可以把GA 算法的自然选择策略融入其中，对PSO 进行改进，加速收敛。

（2）粒子在进行速度更新时，包含了搜索速度快慢与搜索方向2 个方面，因此可以融入GA 的交叉思想，在不改变粒子速度快慢的前提下，改变搜索方向的更新规则，这样可以提升粒子的记忆与认知能力。

通过上述方法对PSO 的改进后，形成GPSO 算法，该算法可以减少记忆性对粒子运动的干扰，防止出现重复路线，有效提升收敛速度，避免发生局部最优的问题。通过GPSO 能够得到深度神经网络模型中权值与阈值的最佳初始值，进而可以利用优化后的深度神经网络完成对机器人定位误差的估计。

综上所述，GPSO-DNN 网络模型构建过程可以描述为

（1）对机器人定位误差样本进行归一化操作，并将样本分为训练与测试两部分。

（2）根据式（9），对DNN 网络的隐含层节点个数的取值大致范围进行初步确定，并在该范围内利用遍历的方法，获取最优的隐含层层数与节点个数。

（3）通过GPSO 算法，获取目前DNN 网络结构下最佳权值与阈值。

（4）对获取到最佳权值与阈值的DNN 网络实行训练与测试操作，并对其网络结构与估计结果进行留存。

（5）按照顺序对DNN 网络中隐含层层数与节点个数取值范围内的所有元素进行遍历操作，如果不符合遍历终止要求，那么返至第（3）步；如果符合遍历终止要求，那么终止遍历操作，选取精度最优的深度神经网络结构与估计数据。

1.3.2 机器人定位误差估计与补偿的实现

利用GPSO-DNN 网络模型对机器人定位误差进行估计与补偿的过程如下：

（1）在机器人工作空间内，利用LHS 方法对机器人位姿进行采样规划，获取机器人定位采样点理论位姿Psample；

（2）利用Psample对GPSO-DNN 进行训练，得到最优的GPSO-DNN 网络模型；

（3）将机器人末端理论位姿Ptarget输入至已训练好的GPSO-DNN 网络模型内，获取到机器人定位误差估计值Etarget；

（4）对机器人末端理论位姿坐标反向迭加Etarget，这样便可得到经过补偿后的机器人末端位姿坐标P，并将其传输至机器人，至此便实现了机器人定位误差的补偿。

2 实验结果与分析

以某六自由度智能机器人作为实验对象，该机器人整体机身重量为25 kg，臂展长度为75 cm，额定负载为20 kg，驱动方式为电气驱动，机械爪是第6 个自由度，也是该机器人的末端执行器。

为了验证本文方法的有效性，实验对该机器人进行了定位误差估计与补偿，并进行了物体抓取测试。实验随机选择1000 个目标点作为GPSO-DNN网络模型的训练样本，150 个目标点作为测试样本，其他相关参数如表1 所示，实验结果如图1、图2 所示。由图1、图2 可知，利用本文方法对该机器人的17 处位置补偿点与6 个关节进行了相应的移动位置与关节角度误差补偿，并将误差补偿后的结果传送至该六自由度机器人上，使其实现了对目标物体的精确抓取。由此可以看出，通过本文方法能够有效补偿机器人的定位误差，进而保障机器人可以顺利完成指定工作。

图1 机器人定位误差补偿情况Fig.1 Compensation for robot positioning error

图2 机器人抓取物品Fig.2 Robot grasping items

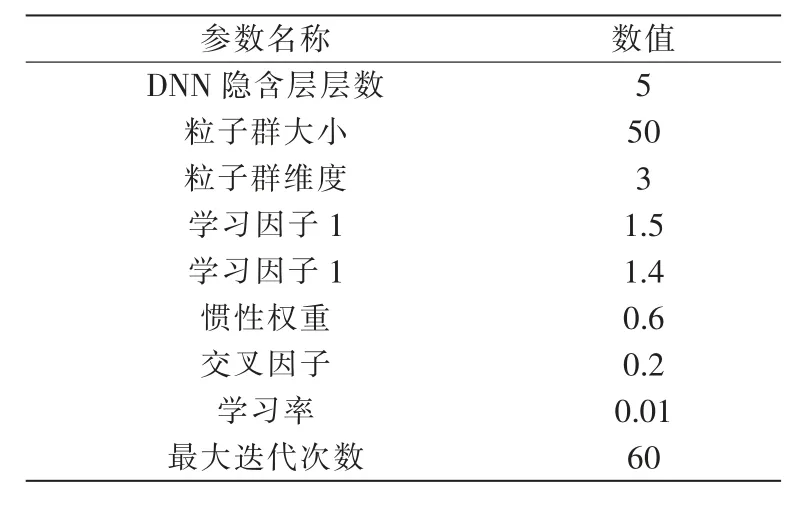
表1 实验参数设置Tab.1 Experimental parameter settings

为了衡量本文方法所提GPSO-DNN 网络模型的性能，实验对该六自由度机器人工作时历史数据进行了采样，并将获取的800 个数据样本作为GPSO-DNN 网络模型的训练样本，对该网络模型的训练损失情况进行了测试，得出的结果如图3 所示。由图3 可知，GPSO-DNN 网络模型训练损失随着迭代次数的增加而下降。本次实验共计迭代140次，前40 次迭代，网络损失下降幅度较大；当迭代次数在40～100 次之间时，GPSO-DNN 网络模型训练损失下降趋势变缓；而当迭代次数大于100 次之后，GPSO-DNN 网络模型的网络波动较小，逐渐呈收敛态势且训练损失也趋于0。由此说明GPSO-DNN模型网络损失小，收敛速度快。

图3 GPSO-DNN 训练损失情况Fig.3 GPSO-DNN training loss situation

不同类型机器人误差补偿后的定位精度如图4所示。由图4 可知，通过本文方法在不同数量采样点条件下，对不同类型机器人进行定位误差补偿后，随着采样点数量的增加机器人定位精度逐步提升。尤其当采样点数量为330 时，三种类型的机器人定位精度均在99.8%以上，即使是在采样点数量仅为30 时，定位精度也达到了99%，由此可以看出，本文方法具有较高的准确性与稳定性。

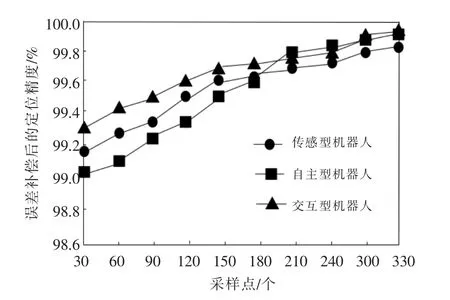
图4 不同类型机器人误差补偿后的定位精度Fig.4 Positioning accuracy of different types of robots after error compensation

3 结语

随着科技的更新，机器人更多地被应用于复杂的工作环境中，这便促使人们对机器人定位精度的要求愈加严格，为提高机器人的定位精度，本文提出一种基于深度学习网络的机器人定位误差估计与补偿方法。该方法运用具有较强学习能力的深度神经网络，对机器人定位误差进行预测估计，并对该误差进行相应补偿，以此实现机器人的精准定位。通过实验证明，本文方法在机器人定位误差补偿方面有着较好的表现，比较适合用于此类问题的解决。