灰色组合预测模型优化及科技人才需求预测

王晓颖　苟小义　曾波

摘 要：科技人才需求预测是国家合理制订人才政策的重要依据。为此，本文基于科技人才需求的数据特征，构建适用于科技人才需求预测的新型离散灰色模型FODGM（r，1，kθ，u），该模型实现了系统发展灰信息非线性规律的较好反映以及累加阶数作用范围全实域拓展，缓解了原始序列中极值对模型性能的影响，能够有效模拟科技人才需求的发展趋势与演变规律。应用该模型对我国科技人才需求量进行预测，结果显示未来我国科技人才需求量呈逐步上升趋势，预计2026年我国科技人员全时当量将达729.258万人年，科技人才需求端压力较大。相关部门可以根据预测结果制定缓解我国科技人才需求端压力的对策。

关键词：科技人才需求预测；离散灰色模型；模型结构；非线性修正项；参数组合优化

中图分类号：F272.1；C964.2；N941.5 文献标志码：A 文章编号：1674-8131（）0-0094-14

引用格式：王晓颖，苟小义，曾波.灰色组合预测模型优化及科技人才需求预测［J］.西部论坛，2023，33（3）：94-107.

WANG Xiao-ying， GOU Xiao-yi， ZENG Bo. Optimization of grey combination forecasting model and forecasting the demand for scientific and technological talents［J］. West Forum， 2023， 33（3）：94-107.

一、引言

科技人才是一种广义的，随时代要求变化而改变的动态概念［1］，其常指拥有科学知识与技术、具有科学素养和能力及道德的人，是经济社会发展的重要资源与基础保障［2］。科技人才需求预测是人才培养、政策制定等的科学依据与重要基础。科技人才需求的预测方法主要有神经网络模型［3］、回归模型［4-5］以及灰色预测模型［6］等。然而，科技人才需求量具有非线性发展特征［7］，并受多种难以定量描述因素的影响［8］。因此，研究者常用GM（1，1）模型来预测科技人才需求量［9］，然而，GM（1，1）模型将灰作用量b视为影响系统发展的所有灰信息［10］，导致建模过程中忽略了部分原始数据的非线性信息。

灰色系统理论是由华中工学院邓聚龙教授在1982年提出，主要解决“小样本，不确定性”系统的分析、预测、决策与控制问题［11］。灰色预测是灰色系统理论的一个重要分支，GM（1，1）模型因为其简单的模型构建和高效的预测能力获得了众多学者的青睐。然而，GM（1，1）模型本身也存在一些缺陷，例如对于原始数据要求高，模型预测结果不稳定等。在现实生活中，数据呈现复杂多变的情况，在GM（1，1）模型的基础上需要提高其模拟精度与适用范围。为此，学者们进行了GM（1，1）模型结构拓展的研究，取得了一系列的学术成果。其中，谢乃明和刘思峰提出了离散灰色预测模型DGM（1，1）［12］，并研究了其与传统GM（1，1）模型的关系。崔杰等针对近似非齐次指数特征序列构建了NGM（1，1，k）模型，进一步拓展了GM（1，1）模型的适用范围［13］。Zeng将线性修正项引入传统GM（1，1）模型，提出一种三参数离散灰色预测模型TDGM（1，1），显著提高了其建模能力和适用性［14］。虽然TDGM（1，1）模型较传统模型有了一定的改进，但是由于忽略了项数k的非线性关系，在处理非线性原始序列时表现仍然较差。为了进一步提高模型的预测精度，Zeng在 TDGM（1，1）的基础上增加了非线性修正项，发展出一种四参数离散灰色模型FDGM（1，1，k2，r）［15］，该模型对非线性原始序列具有更好的模拟性能。

这些拓展与改进不仅提高了GM（1，1）模型的预测精度和适用范围，还为灰色预测模型的发展提供了新的思路，但仍然存在一些改进的空间。为此，本文从科技人才需求量的演变特征出发，对FDGM（1，1，k2）模型的缺陷进行弥补，构建新型优化离散灰色预测模型FODGM（r，1，kθ，u）。新模型结构由线性、非线性作用项以及随机扰动项构成，由此反映影响系统发展的所有灰信息，实现了系统发展灰信息非线性规律的较好反映以及累加阶数作用范围全实域的拓展，缓解了原始序列中极值对建模的影响，可以更加全面、更加精准地进行预测。应用新模型对我国科技人才需求进行预测，并与其他几个预测模型的结果进行比较，验证了其預测的有效性，可以提供更加准确的结果，以帮助政府更好地了解和应对科技人才需求的变化。同时也验证了该预测模型具备科学性和实用性，为不同类型的预测系统提供了一种有效的方法，并对于灰色预测系统的发展具有积极的意义。

单变量灰色系统中，变量描述了系统的演化规律，是系统在诸多复杂外部因素共同作用下的结果。系统发展的影响因素是“因”，系统所体现出的变化结果是“果”。在控制论中，前者称为输入，后者称为输出［17］。对FODGM（r，1，kθ，u）模型而言，线性作用项bk、非线性作用项kθd及灰色作用量c组成的函数构成了输入，代表了影响系统发展的所有灰信息。不同作用量分别表征了系统发展的线性、非线性及随机性，特别地，非线性作用项kθd含待定指数θ，能动态调节系统输入。输出变量为x（0）（k），其通过r-AGO及u-MEAN来动态调节灰因。其中，r-AGO为实数域灰色生成处理，能弱化随机性；u-MEAN为含待定系数的紧邻生成处理，能改善平滑性。系统输入、输出之间的关系如图2所示，根据其间关系可得到FODGM（r，1，kθ，u）模型的定义。特别地，公式（3）含三大待定系数（θ、u、r），使用参数组合优化思路求解，达到根据原始数据特征动态匹配从而得到全局最优模型的目的。

2. FODGM（r，1，kθ，u）模型参数估计

四、FODGM（r，1，kθ，u）模型的应用：我国科技人才需求预测

本文基于官方网站公布数据的可获得性，以R&D人员全时当量反映我国科技人才的需求量，数据来源于相应年度的统计年鉴。如表1所示。我国R&D人员全时当量的增长具有较大的波动性，最低增长率为1998年的-9.15%，最高增长率为2005年的18.39%，增长率区间跨度超过27%，具有较明显的非线性特征，容易导致传统GM（1，1）模型的预测效果不理想。

1. FODGM（r，1，kθ，u）模型建模

为同时验证FODGM（r，1，kθ，u）模型的模拟及预测性能，本文将表1中的原始数据进行分组：X（0）=［x（0）（1），x（0）（2），…，x（0）（t），x（0）（t+1），…，x（0）（n）］。为体现新模型建模的稳健性，根据R&D人员全时当量数据，预留不同长度数据进行建模。为验证FODGM（r，1，kθ，u）模型较现有灰色预测模型的优越性及其对FDGM（1，1，k2）模型结构和参数缺陷的优化，将常用预测模型GM（1，1）、新模型的基础模型FDGM（1，1，k2）、仅优化单一参数u的FODGM（1，1，k2，u）模型作为对比模型。各模型建模结果如表2所示，并根据表2数据绘制各模型不同样本区间下的误差折线图，如图3所示。

根据表2与图3，新模型在不同的样本区间下均具有最小的综合误差，表明新模型较其余模型具有最优的建模性能及稳健性。由于篇幅所限，后文仅展示选取前26个数据组成的建模序列X（0）S、预留后1个数据组成预测序列为X（0）F的详细建模过程。根据FODGM（r，1，kθ，u）模型的建模步骤，使用MATLAB及PSO算法（MATLAB自带），计算得FODGM（r，1，kθ，u）模型最优参数组合数值为r*=-0.373 333、u*=0.314 490、θ*=-0.016 398。根据定理1构造模型基本参数估计矩阵B和Y，并计算得出基本参数列如下：

2.FODGM（r，1，kθ，u）模型检验及对比分析

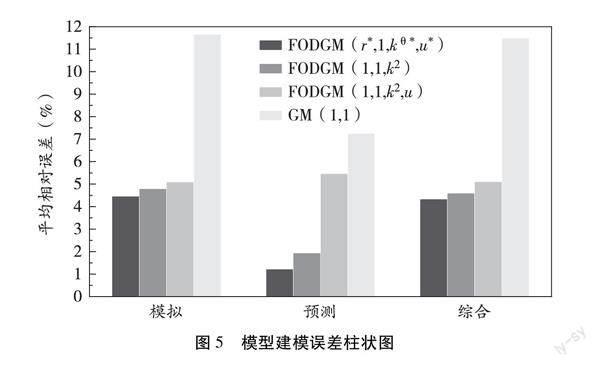
同样地，使用MATLAB自带PSO程序对FDGM（1，1，k2）和FODGM（1，1，k2，u）模型中待定参数寻优，分别为r=0.197 829、u=1。其余建模结果信息如表3所示，并绘制各模型建模误差柱状图如图4所示，其中（0）为模型得到的模拟（预测）數据，Δk为（0）相对误差（Δk=（0）（k）－x（0）（k）/x（0）（k）×100%）。

根据上述建模结果误差，新模型的模拟检验、预测检验及综合性能较其余模型均更优，表明新模型对我国科技人才需求的预测有着显著的优越性，更能准确预测未来趋势。为了进一步说明本文提出的新模型在科技人才需求预测中的优势，与已有的相关研究结果进行比较，如表4所示。可以看出GM（1，1）模型预的测结果不稳定，一是因为预测的对象不一样，二是因为GM（1，1）模型本身对原始数据要求较高。在本文中，应用GM（1，1）模型的预测效果远不如新模型FODGM（r，1，kθ，u）。

综上所述，与现有的相关研究相比，本文提出的科技人才需求量预测模型考虑了更多因素的影响，具有更高的预测精度和可靠性，有助于政策制定者更好地把握科技人才市场的变化趋势和未来发展方向，进而促进我国科技人才的可持续高质量发展。

3. FODGM（r，1，kθ，u）模型预测结果

如表5所示，从预测未来的数据可以看出，GM（1，1）模型受其模型结构的制约，预测结果呈现指数增长趋势。FDGM（1，1，k2）、FODGM（1，1，k2，u）与新模型由于非线性项的引入，具有处理复杂序列规律的能力，呈现出更科学的预测结果。然而，FDGM（1，1，k2）与FODGM（1，1，k2，u）模型固化的非线性项结构局限了模型性能和作用空间，导致作用项指数无法依据原始序列的数据特征进行匹配，缺乏动态可调性。此外，根据现有数据的模拟及预测检验情况来看，新模型较FDGM（1，1，k2）与FODGM（1，1，k2，u）具有更优的预测检验性能。因此，新模型的预测结果更具科学性与合理性。根据预测结果可知，未来我国R&D人员全时当量呈现逐步上升趋势，表明我国未来科技人才需求量处于上升阶段，且增幅与历年趋势相近，科技人才需求端压力显著。

五、结论

科技人才需求量具有非线性发展的特征，并受多种难以定量描述因素的影响，现有GM（1，1）模型将灰作用量b视为影响系统发展的所有灰信息，建模过程中容易忽略部分原始数据间的非线性关系，从而导致建模效果不理想。为此，本文在分析现有模型缺陷的基础上，构建了新型优化离散灰色预测模型FODGM（r，1，kθ，u）。新模型弥补了现有模型的不足，实现了系统发展灰信息非线性规律的较好反映，并通过参数组合优化进一步提升了模型建模性能。将新模型用于我国科技人才需求量预测，预测结果显示未来我国科技人才需求量将会呈现持续稳步上升的趋势。预计到2026年，我国科技人员全时当量将达到729.258万人年。这一结果表明科技人才需求端的压力将会显著增加，也为进一步合理制定相关政策提供了科学依据。相关部门可以基于预测结果制定相关政策，缓解科技人才需求端的压力，避免人才资源的浪费，为我国科技事业发展提供有力的人才支持，进而促进科技进步和创新驱动发展。

本文提出的新预测模型FODGM（r，1，kθ，u）在预测科技人才需求量方面具有一定的科学性和实用性，但也存在一些不足之处。首先，新预测模型建立在历史数据的基础上，因此对于突发事件、政策变化等因素的影响预测能力相对较弱。其次，预测模型的精度还有待提高。为进一步提高新模型预测的准确性和实用性，可以从加强对新技术、新趋势的研究和建立更加完整、准确的数据集两个方面进行探索和改进。综上所述，灰色预测是一个复杂的问题，需要考虑数据的演变规律以及模型的适用范围。随着技术的不断发展和经验的不断积累，灰色预测模型的准确性和实用性将会不断提高。

参考文献：

［1］杜谦，宋卫国.科技人才定义及相关统计问题［J］.中国科技论坛，2004（5）：137-141.

［2］ 瞿群臻，王嘉吉，唐梦雪，等.基于组合模型的“十四五”期间中国科技人才需求预测［J］. 科技管理研究， 2021，41（21）：129-135.

［3］ 张建勇，赵涛.基于BP神经网络的科技人才需求预测［J］.科技管理研究，2009，29（8）：501-502.

［4］ ［1］李锡元，王艳姣.重点产业海外高层次人才需求研究——以湖北省汽车和钢铁产业为例［J］.科技进步与对策，2014，31（8）：135-139.

［5］ AKINNULI B O，APALOWO R K. Regression analysis based effective manpower planning methodology：a case study［J］. Journal of Engineering Research and Reports，2018：1-12.

［6］ LI L，WANG R，LI X. Grey GM（1， 1，βk） model and its application in R&D personnel［J］. Journal of Grey System，2017，29（1）：120-134.

［7］ 白旭光. 基于灰色系统理论的风险投资人才需求预测研究——以山西省为例［J］.系统科学学报，2017，25（4）：67-69.

［8］ 闵惜琳.基于灰色预测模型GM（1，1）的人才需求分析［J］.科技管理研究，2005（6）：72-74+77.

［9］ 尹逊震，门可佩.离散灰色模型在科技人才资源预测中的应用［J］.科技进步与对策 2007（10） 204-206.

［10］YIN K，GENG Y，LI X. Improved grey prediction model based on exponential grey action quantity［J］. Journal of Systems Engineering and Electronics，2018，29（3）：560-570.

［11］邓聚龙.灰色控制系統［J］.华中工学院学报，1982（3）：9-18.

［12］谢乃明，刘思峰.离散GM（1，1）模型与灰色预测模型建模机理［J］.系统工程理论与实践，2005（1）：93-99.

［13］崔杰，党耀国，刘思峰.一种新的灰色预测模型及其建模机理［J/OL］.控制与决策，2009，24（11）：1702-1706.

［14］ZENG B，LI C. Forecasting the natural gas demand in China using a self-adapting intelligent grey model［J/OL］. Energy，2016，112：810-825.

［15］ZENG B，LI H. Prediction of coalbed methane production in China based on an optimized grey system model［J］. Energy & Fuels，2021，35（5）：4333-4344.

［16］曾波，余乐安，刘思峰，等.灰色累加算子与灰色累减算子的统一及其应用［J］.系统工程理论与实践，2021，41（10）： 2710-2720.

［17］曾波，李树良，孟伟.灰色预测理论及其应用［M］.北京：科学出版社，2020.

［18］孟伟，曾波.分数阶算子与灰色预测模型研究［M］.北京：学出版社，2015.

［19］万春林，张卫.基于改进粒子群算法的基数受限最优化问题研究［J/OL］.统计与决策，2021，37（20）：20-24.

［20］姚娟， 刘鸿渊， 刘建贤.科技创新人才区域性需求趋势研究——对四川、陕西、上海的预测与比较分析［J］. 科技进步与对策，2019，36（14）：46-52.

［21］卞永峰，李恩平.基于组合预测模型的山西省转型期紧缺科技人才需求预测研究［J］.科技管理研究，2013，33（21）：41-45.

［22］王维，李钰.最优组合预测在四川省人才需求预测中的应用［J］.价值工程，2005（3）：9-12.

［23］王五祥，张维，崔和瑞，等.多变量灰色模型MGM（1，n）在R&D投资预测中的应用［J］.研究与发展管理，2006（2）：92-96+103.

Optimization of Grey Combination Forecasting Model and Forecasting the Demand for Scientific and Technological Talents

WANG Xiao-ying1， GOU Xiao-yi2， ZENG Bo3

（1. School of New Media Art， Chongqing Finance and Business College， Chongqing 401320， China; 2. College of Economics and Management， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， Jiangsu， China; 3. School of Management Science and Engineering， Chongqing Technology and Business University， Chongqing 400067， China）

Abstract： In recent years， China has proposed the task of promoting technological innovation and improving the quality of development to achieve the innovation-driven development strategy and consolidate the foundation of the real economy. As an important power source and core element to promote the innovation-driven development strategy， scientific and technological talents are conducive to stimulating new economic growth points and releasing the endogenous power of the economy while promoting scientific and technological progress， thus promoting the structural transformation and high-quality economic development of China. The demand forecast for scientific and technological talents is an important basis for the cultivation of scientific and technological talents and policy formulation. The demand for scientific and technological talents has typical non-linear development characteristics and is also influenced by a variety of factors that are difficult to describe quantitatively. Therefore， the grey prediction model with the characteristics of small data and poor information modeling is gradually becoming a common method for forecasting the demand for scientific and technological talents.

Although the grey prediction model has the advantages of simple structure and wide applicability， there are still some shortcomings， such as unstable model prediction performance and poor model compatibility. Therefore， starting from the characteristics of the demand for scientific and technological talent data， this article proposes a new grey prediction model FODGM（r，1，kθ，u） with dynamic adaptability based on the defect analysis of the FDGM（1，1，k2） model. The new model adds a nonlinear correction term to the FDGM（1，1，k2） model， which improves the model‘s simulation performance of nonlinear original series; the dynamic adaptivity of the model is improved by extending the original first-order accumulation to fractional-order. The new model achieves a better simulation of the nonlinear law of grey information of system development and the totally real number fields expansion of the accumulating order action range， which alleviates the influence of extreme values in the original sequence on the model performance and improves the compatibility of the model structure and the stability of the prediction results.

The national research and development （R&D） personnel of full-time equivalent is selected to reflect the demand for scientific and technological talents in China. In order to reflect the robustness of the new model， data of different lengths are reserved for simulation and prediction modeling， and compared with other models. The results show that the FODGM（r，1，kθ，u） model has the smallest comprehensive error in different sample intervals. Finally， the FODGM（r，1，kθ，u） model was applied to predict the future demand for R&D personnel in China. The results showed that the demand for R&D personnel in China is gradually increasing in the future. It is expected that the full-time equivalent of R&D personnel in China will reach 7.29258 million person-years in 2026， indicating significant pressure on the demand side of scientific and technological talents. To this end， relevant countermeasures and suggestions have been proposed. The research results have positive significance in promoting the sustainability of Chinas science and technology industry， alleviating the pressure on the demand for scientific and technological talents， and promoting the healthy development of Chinas science and technology industry. It has important value for enriching， developing， and improving the theoretical system of grey prediction models.

Key words： demand forecast of scientific and technological talents; discrete grey model; model structure; nonlinear correction term; parameters combination optimization

CLC number：

F272.1；C964.2；N941.5 Document code：A Article ID：1674-8131（）0-0094-14

（編辑：朱德东）

收稿日期：2023-02-23；修回日期：2023-04-28

基金项目：重庆市技术预见与制度创新专项项目（cstc2021jsyj-zdxwtAX0009，CSTB2022TFII-OIX0051）；重庆市教委教育教学改革研究项目（222178）；重庆市教委科学技术研究重点项目（KJZD-K202202102）；重庆市研究生科研创新项目“数字经济和实体经济融合对成渝双城地区制造业绿色创新的影响研究”

作者简介：王晓颖（1977），女，重庆渝中区人；副教授，博士，主要从事管理学研究；Tel：023-88968667，E-mail：xiaoyingwang@hotmail.com。

苟小义（1996），女，四川内江人；博士研究生，主要从事灰色预测建模研究；Tel：18328074625，E-mail：gxy18328074625@163.com。

曾波（1975），男，四川内江人；教授，博士，主要从事预测理论与方法的研究；Tel：023-62769347，E-mail：15922951705@163.com。