附加连接对主动指向超静平台控制效果的影响

樊茂，汤亮，2，*，关新，2，张科备，2

1.北京控制工程研究所，北京 100190

2.空间智能控制技术国防科技重点实验室，北京 100190

卫星平台姿态控制系统的高指向精度、高稳定度与高敏捷性能是未来地外行星观测与激光通信等航天任务的必然选择［1-2］。目前制约卫星平台快速稳定与扰动抑制能力的因素主要有3 点：①挠性附件的低频振动（0.1～10 Hz）与执行机构的高频扰动（10～200 Hz）对平台扰动抑制能力的影响；② 航天器在轨高速运行对指向精度与敏捷机动能力的影响。③卫星附件耦合运动对姿态稳定性的影响。

许多工程师与学者都对主动指向、主被动隔振装置进行了大量的研究与工程应用。例如詹姆斯韦伯空间望远镜（James Webb Space Tele‐scope，JWST）［3-4］安装有多组主动非接触式隔振机构，来减少星体执行机构振动对光学载荷姿态指向精度的影响，可实现40 Hz 以上80 dB 的被动振动衰减；Kepler 望远镜采用Stewart 平台对主镜进行隔振，平台作动器与载荷主镜相连实现微振动隔离抑制，姿态指向长期稳定度可达0.009″［5］。为了实现对地外行星的探索，ACCESS（Actively-Corrected Coronagraph for Exoplanet System Studies，ACESS）卫星平台［6-7］提出了以姿态控制系统、隔振指向平台和精确调节镜组成的三级指向控制系统，可实现0.1×10−3″的指向控制精度。LUVOIR（Large UV Optical Infrared Surveyor）空间望远镜［8-9］采用非接触式的自由飞行载荷（Disturbance Free Payload，DFP）［10］振动隔离与精确指向系统（Vi‐bration Isolation and Precision Pointing System，VIPPS），实现了载荷与卫星平台的物理隔离与姿态精确指向。从以上工程应用实例可以看出，美国等航天强国正在积极试验基于多级控制平台的高精高稳高敏捷性能的航天器。

针对多级卫星平台的动力学建模与控制问题，大量学者已经对其进行了研究［11-20］。文献［21］研究了一种基于VIS（Vibration Isolation Sys‐tem）隔振系统的优化方法，文中提出的VIS 隔振系统与优化方法可显著减少振动对大型空间望远镜的影响；文献［18］建立了PVCP（Pointing and Vibration Control Platform）平台，提出了平台载荷一体化控制方法，实现了载荷的精确指向与振动隔离；文献［22］提出了多级卫星平台一体化控制方法，该方法使载荷的指向精度与稳定度较平台至少提升了一个数量级，并通过试验的方式验证了所提出方法的有效性；文献［23］建立了基于磁悬浮作动器的多级卫星平台动力学模型，并利用有限时间控制理论设计了具有带宽限制的控制器，实现了载荷的快速机动与振动隔离；文献［24］提出了一种基于干扰观测器设计的主动指向超静平台鲁棒控制方法，实现了无载荷姿态敏感器场景下的高精度指向。

但在实际工程中，为了保持卫星平台和载荷之间的通信、供电与散热等需求，载荷与卫星平台之间存在线缆、热管等附加连接。目前只有少数学者研究了卫星多级控制平台的柔性线缆建模问题［25］，尚未发现有学者对存在线缆、热管等附加连接时的卫星多级控制系统的控制性能进行理论与试验的对比分析研究。附加连接可能导致系统指向精度、控制稳定性与隔振效果的下降，因此有必要对该问题进行研究。

本文针对星体与载荷之间存在的线缆、热管等附加连接问题，分析了附加连接对主动指向超静平台控制性能的影响。首先，利用牛顿欧拉方法建立了超精超稳超敏捷卫星多级动力学模型，将线缆热管连接等效为附加刚度，建立附加连接的力学模型，仿真分析了附加连接对系统隔振效果、稳定性的影响，为试验的设计提供理论基础。其次，为进一步掌握附加连接对系统控制性能产生的影响，测量线缆、热管实际刚度，设计试验方案对主动指向超静平台开展控制系统的全物理仿真试验。试验结果表明，理论分析结论与试验结果吻合性较好，线缆、热管等小刚度的附加连接对主动指向超静平台控制系统的稳定性、指向精度与调节时间无明显影响，试验中采取的线缆、热管装配措施与安装布局可供整星安装参考。最后，针对附加连接存在下的平台与载荷之间耦合与振动抑制问题，提出了一种自适应预设性能非线性控制器，数值仿真结果表明，本文提出的控制器有效改善了载荷、平台之间的耦合问题，进一步提升了载荷姿态的敏捷机动、稳定跟踪与高精度指向能力。

1 系统组成与动力学建模

1.1 系统组成

超精超稳超敏捷卫星平台如图1 所示，在卫星平台姿态控制的基础上，增加主动指向超静平台二级控制实现载荷姿态的快速机动与稳定控制。

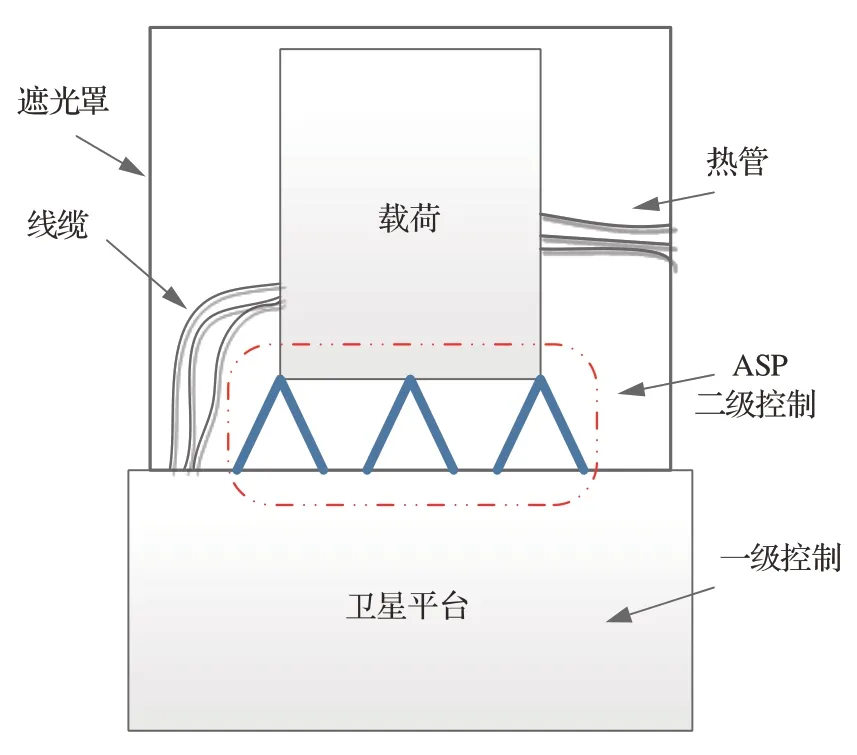
图1 超精超稳超敏捷卫星平台Fig.1 Ultra-agile ultra-stable and ultra-pointing multistage satellite

超精超稳超敏捷卫星平台共有2 级控制，一级控制采用传统卫星平台的姿态控制系统，实现了整体卫星姿态指向的粗调整。二级控制为主动指向超静平台（ultra-Agile ultra-Stable and ultra-Pointing，ASP）。主动指向超静平台由多个作动器按照一定构型组成，利用作动器的直线运动实现对载荷姿态指向的控制。

为了保持卫星平台和载荷之间的通信、供电与散热等需求，载荷与卫星平台之间有线缆、热管等附加连接。

1.2 载荷、卫星平台动力学模型

为了分析附加连接对超精超稳超敏捷卫星的影响，首先建立星体、载荷刚体动力学模型。载荷的平动、转动动力学方程如式（1）、（2）所示

卫星平台刚体动力学如式（3）所示［26］

1.3 主动指向超静平台

主动指向超静平台连接卫星平台和载荷，其构形如图2 所示。

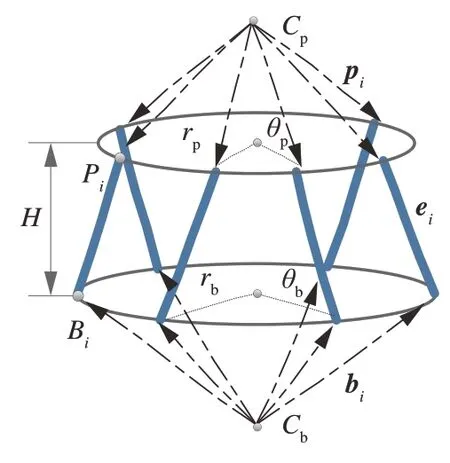
图2 主动指向超静平台作动器构型Fig.2 Structure of active steering and ultra-quiet platform

主动指向超静平台的结构示意图如图2 所示，其中Pi(i=1，2，…，6)为作动器与载荷平台的连接点；Bi(i=1，2，…，6)为作动器与卫星平台的连接点；rp表示载荷安装面半径；rb表示星体安装面半径；θp表示载荷安装面定位角；θb表示星体安装面定位角；H表示平台的高度；pi表示作动器上端与载荷平台连接点的位置矢量；bi表示作动器下端与基础平台连接点的位置矢量。定义向量vi=pi−bi为作动器下端到上端的向量，作动杆的长度li=‖vi‖，沿作动器方向的单位向量表示为ei=vi/li。

单个作动器原理如图3 所示，作动器采用电机加膜簧结构。作动器的输出力由2 部分组成，第1 部分为膜簧的弹性被动力，第2 部分为作动器电机的输出主动力。在实际工程应用中，作动器执行机构在设计原理上就避免了非线性因素对系统的影响，设计出的作动器具有无摩擦、无间隙、分辨率高等特点，试验结果表明，作动器线性性能出色，因此在理论建模分析中可忽略非线性因素。

图3 作动器动力学原理图Fig.3 Schematic diagram of actuator dynamic

第i个作动器支杆的膜簧刚度为ki，阻尼系数为ci。令fli，fai，fci，fki分别表示作动器末端输出力、作动器音圈电机输出控制力、作动器阻尼力、作动器弹性力fki=kiδli，则作动器的输出力可表示为

主动指向超静平台作动器输出力列阵可表示为

式中：Fc表示阻尼力列阵；K表示刚度矩阵；Fk表示弹性力列阵；C表示阻尼矩阵；Fl表示输出力列阵；Fa表示控制力列阵；δl表示位移增量；表示作动杆长度变化速度。作动器杆长变化的计算公式可以表示为

其中：XP表示载荷平台平动和转动产生的位移和转角；XB表示卫星平台平动和转动产生的位移和转角。因此主动指向超静平台被动环节对载荷产生的回复力为

同理，主动指向超静平台的被动环节对卫星平台产生的回复力为

由式（5）～式（8）的推导可以得到，主动指向超静平台对载荷与卫星平台的作用力由主动环节与被动环节构成，其输出合力可表示为

式中：JP为主动指向超静平台对载荷质心的雅克比矩阵；Jb表示主动指向超静平台对卫星平台质心的雅克比矩阵。

2 附加连接对系统产生的影响

2.1 附加连接刚度理论计算

星体与载荷质心运动与受力关系方程如下所示

式中：Fp1、Tp1、Fb1、Tb1分别表示载荷质心平动力、载荷质心转动力矩、星体质心平动力和星体质心平动力矩；Kpp、Kpb、Kbp、Kbb分别表示载荷刚度矩阵、载荷受力与星体位移的耦合刚度矩阵、星体受力与载荷位移的耦合刚度矩阵和星体刚度矩阵。联立式（6）～式（8）可以分别计算出系统刚度矩阵为。本文将附加连接等效为弹簧刚度模型，附加连接等效模型示意图如图4 所示。

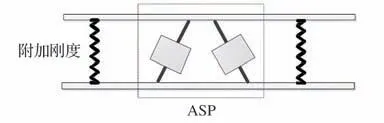
图4 附加连接等效图Fig.4 Additional connection equivalent figure

表1～4 表示无附加刚度与有附加刚度时主动指向超静平台被动环节的合成刚度矩阵。在3.2 节针对线缆、热管的刚度测量试验中可以获得系统附加刚度矩阵数值，如表3、表4 所示，其刚度大约为系统标称刚度的5%～10%，因此选择试验所得附加刚度矩阵进行仿真分析。

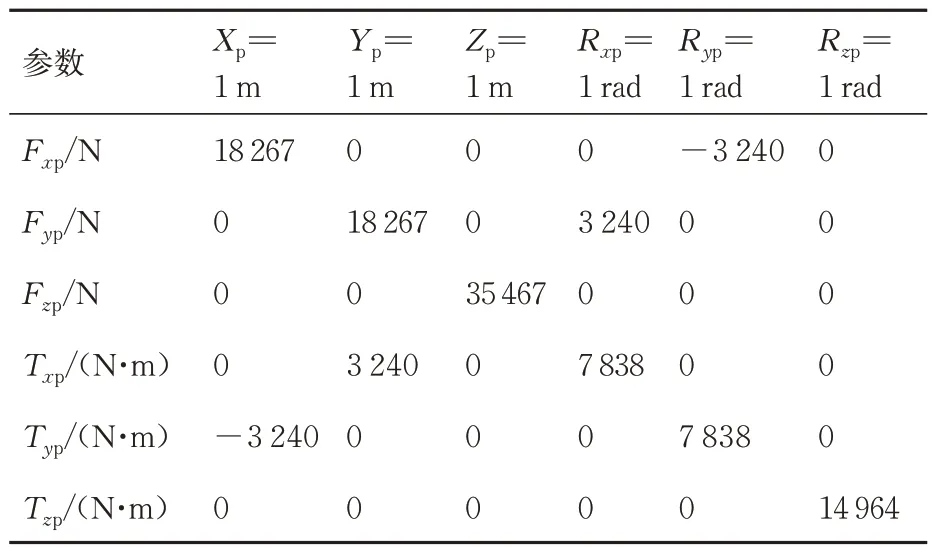
表1 无附加刚度载荷刚度矩阵KppTable 1 Payload stiffness matrix without additional stiffness Kpp

最终，表1 与表3 中的数值相加表示存在电缆连接时的载荷刚度矩阵，表2 与表4 数值相加表示存在电缆连接时的载荷耦合刚度矩阵。

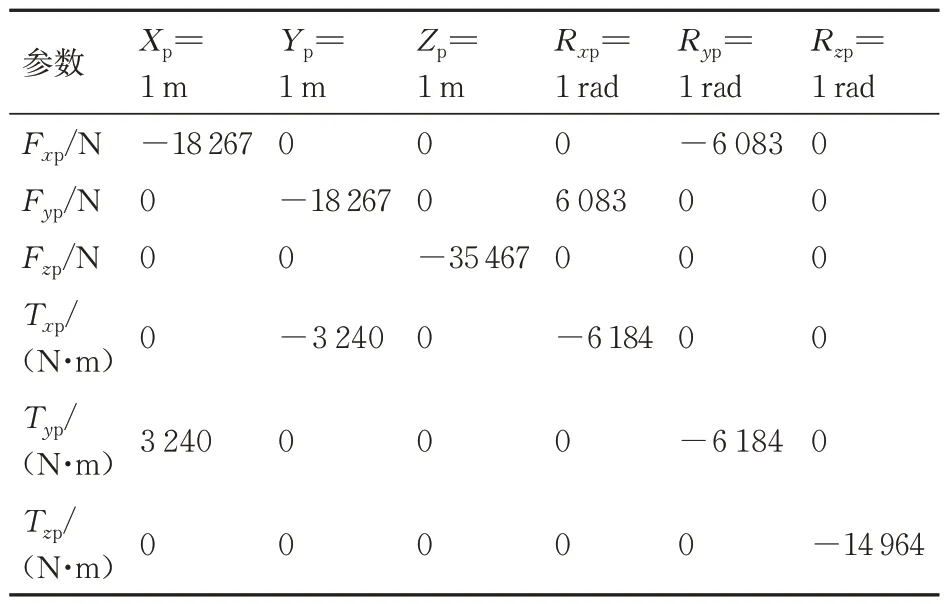
表2 无附加刚度载荷受力星体位移耦合刚度矩阵KpbTable 2 Payload coupling stiffness matrix without ad⁃ditional stiffness Kpb

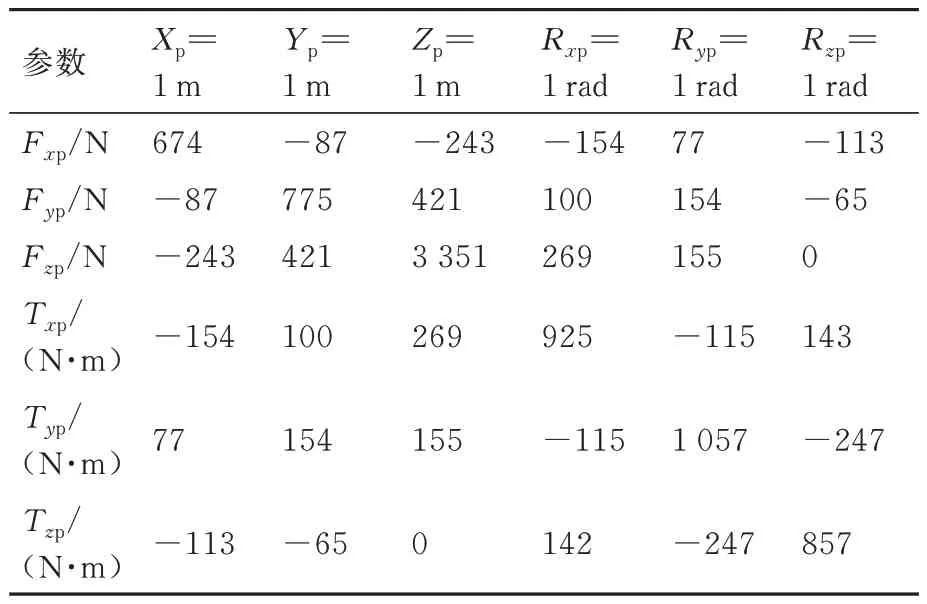
表3 电缆连接产生的载荷附加刚度矩阵Table 3 Payload additional stiffness matrix caused by additional connection

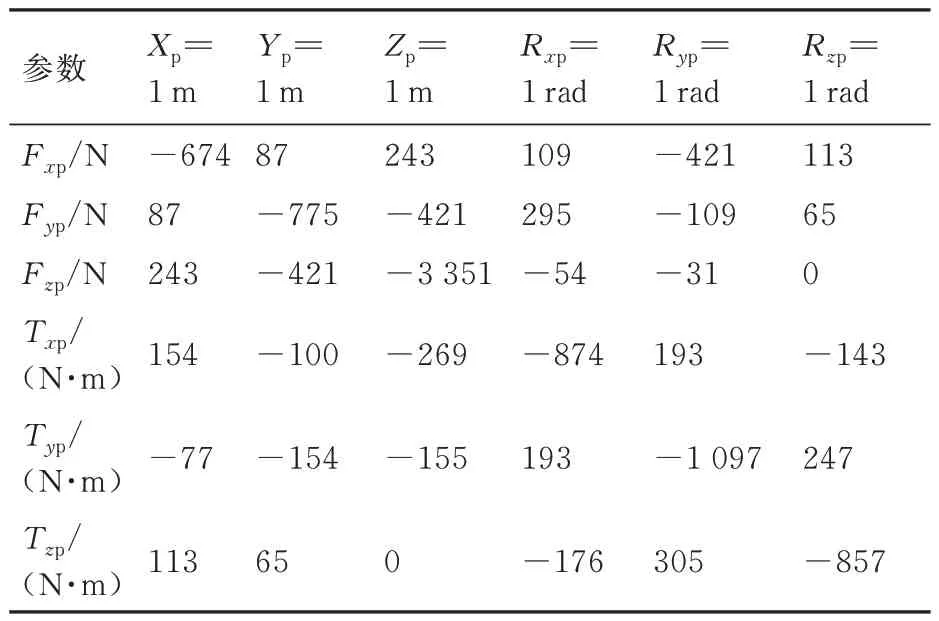
表4 电缆连接产生的载荷受力星体位移耦合刚度矩阵Table 4 Payload additional coupling stiffness matrix caused by additional connection

2.2 开环系统理论分析

以x轴转动方向为例分析开环系统传递函数曲线。x轴开环系统传递函数的输入为未闭环的力矩τpx，输出为载荷姿态角度θpx。x轴开环系统扰动传递率传递函数的输入为下平台姿态角θbx，输出为载荷姿态角θpx。

由图5、图6 可以看出，加入附加刚度的开环扰动传递率曲线放大了耦合现象，转动平动之间振动扰动相互影响，高频阶段的被动隔振效果相应降低；除此之外，附加刚度提升了系统的固有频率，降低了系统低频阶段增益。

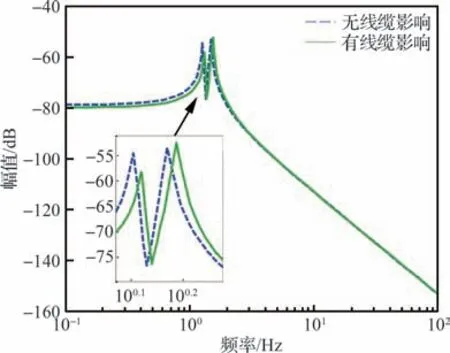
图5 开环系统x 轴转动传递函数曲线对比Fig.5 Open-loop x rotation transfer function curves

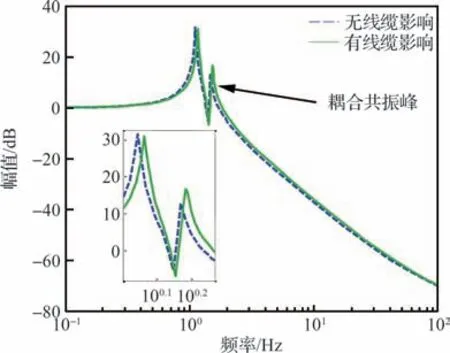
图6 开环系统x 轴转动扰动传递率曲线对比Fig.6 Open-loop x rotation disturbance transmissibility curves

2.3 闭环系统理论分析

超精超稳超敏捷卫星控制框图如图7 所示。卫星平台的姿态控制器设计如下

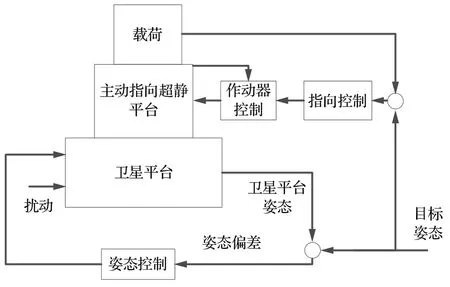
图7 超精超稳超敏捷卫星控制框图Fig.7 Flow chart of ultrahigh precision ultrahigh sta‐bility ultra-agile multi-stage satellite

式中：Kbp1、Kbi1、Kbp1表示卫星平台姿态控制器的控制参数；δθbe、δωbe分别表示卫星平台姿态误差与角速度误差，可由式（13）求出

其中：δqvb表示误差四元数的矢量部分；qb、qbd分别表示卫星平台实际、期望姿态四元数；ωbd、ωb分别为表示在本体系下的卫星平台期望、实际角速度。在大角度机动过程中，可以在控制力矩中进一步加入前馈项。

同卫星平台姿态控制一样，载荷指向控制器如下所示

式中：Kpp1、Kpi1、Kpd1表示载荷姿态控制器的控制参数；δθpe、δωpe分别表示载荷姿态误差与角速度误差，可由式（15）求出

其中：δqvp表示误差四元数的矢量部分；qp、qpd分别表示载荷实际和期望姿态四元数；ωpd、ωp分别为表示在本体下的载荷期望和实际角速度。

根据计算出的载荷指向控制力矩设计作动器分配律，由于载荷指向控制只对姿态方向有控制力矩，对载荷平动方向无力约束作用，因此作动器分配律如下

以x轴转动通道为例，分析闭环系统传递函数曲线。x轴闭环系统传递函数的输入为载荷期望轨迹θpxd，输出为载荷姿态角θpx。闭环系统从图8 中可以看出，附加刚度的加入略微降低了闭环系统低频阶段的增益，对高频阶段影响较小。

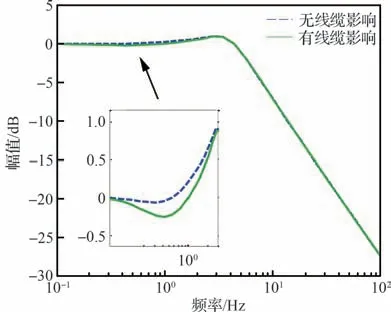
图8 闭环系统x 轴传递函数曲线对比Fig.8 Close-loop x rotation transfer function curves

如图9 所示，附加刚度降低了闭环系统低频阶段隔振效果，对高频阶段影响不大。

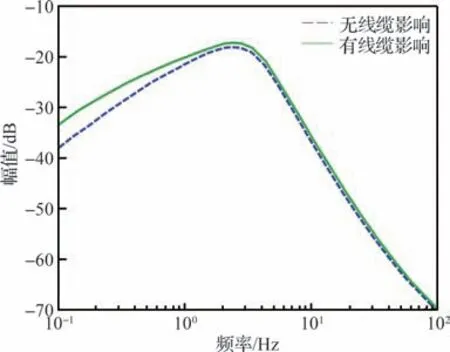
图9 闭环系统x 轴转动扰动传递率曲线对比Fig.9 Close-loop x rotation disturbance transmissibility curves

闭环系统扰动传递率传递函数的输入为下平台姿态角θbx，输出为载荷姿态角θpx。以x轴转动通道为例，分析附加刚度对系统稳定性影响，如图10 所示。x轴幅值稳定裕度由8.41 dB 下降到8.36 dB；相位裕度从35.9°下降到35.2°。

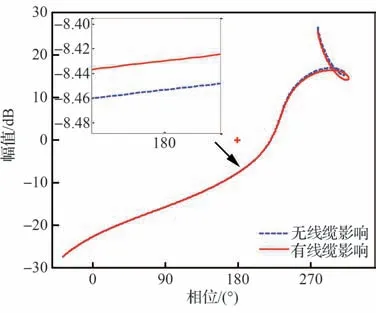
图10 x 轴转动稳定性分析Fig.10 Stability analysis of x rotation channel

从上述理论分析可知，附加刚度略微降低了系统的稳定性与隔振性能，但总体影响不大。

3 物理试验分析

开展全物理仿真试验的主要目的如下：

1）掌握线缆、热管模拟件在一定范围内的拉伸、压缩刚度。

2）评估附加连接对主动指向超静平台控制系统稳定性、指向精度与调节时间的影响。

3）与理论分析结果进行对比，进一步完善理论模型。

3.1 试验系统组成

试验系统由载荷模拟器、6 自由度激振台、测微敏感器、涡流位移敏感器、指向隔振机构作动器组件、自准直仪以及平台控制单元构成。

载荷模拟器用来模拟载荷的力学结构特性，6 自由度激振台用来模拟卫星平台，测微敏感器采样频率≥200 Hz，零偏≤1（°）/h，随机游走系数≤0.000 2（°）/（h1/2）；涡流位移敏感器随机噪声（3σ）<0.7 μm，采样频率≥1 kHz；指向隔振机构作动器直线电机力噪声<0.005 N；自准直仪测量载荷姿态，测量精度0.1″；平台控制单元计算机更新频率≥200 Hz。

试验系统布局如图11 所示，测微敏感器安装于载荷底板上，主动指向超静平台下安装面固定在6 自由度激振台上，上安装面与载荷底板固连，系统通过低频悬吊装置对载荷进行重力卸载，模拟在轨失重状态，使载荷在微低重力工况下进行测试。

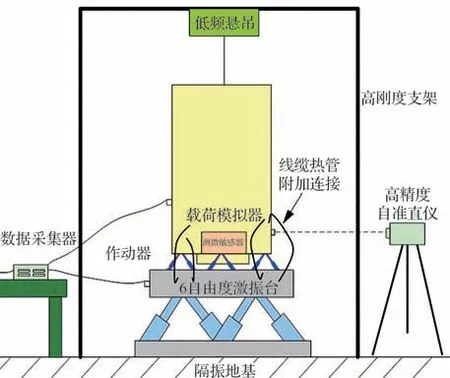
图11 试验系统框图Fig.11 Diagram of experimental system

3.2 线缆热管刚度测量

为了掌握线缆、热管等附加连接的刚度特性，进一步分析附加连接对系统产生的影响，对线缆、热管模拟件的拉伸、压缩刚度进行测量。热管模拟件如图12 所示。

图12 热管模拟件Fig.12 Photo of heat pipe simulator

试验测试中，载荷模拟件与星体之间的附加连接为8 根热管与26 组线缆。其中，每根热管模拟件长度约500 mm，弯折成直径约40 mm、节距约150 mm、圈数约为2 圈的螺旋形；每组线缆模拟件长度约为300 mm，每组52 根共26 组，26 组线缆合成一股连接于激振台与载荷之间。

对安装点初始直线距离为150 mm，安装点外侧长度约为170 mm 的单组线缆模拟件与外侧长度约为400 mm 的单根热管模拟件分别进行压缩、拉伸刚度的测量。记录每向下移动20 mm 过程中线缆、热管的平均刚度。拉伸、压缩刚度如表5 和表6 所示。热管模拟件刚度测量试验如图13 所示。

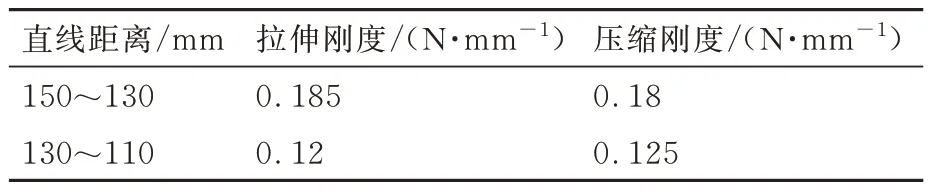
表5 线缆模拟件拉伸、压缩刚度测量值Table 5 Tensile and compression stiffness of cable simulator

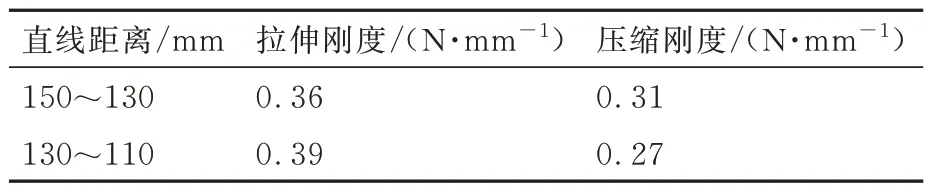
表6 热管模拟件拉伸、压缩刚度测量值Table 6 Tensile and compression stiffness of heat pipe simulator

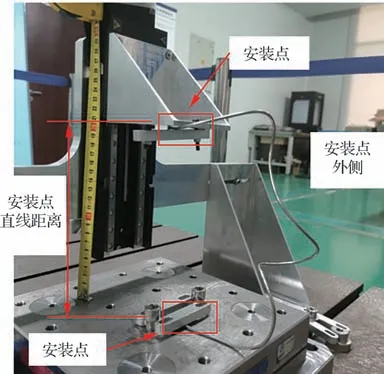
图13 热管模拟件刚度测量Fig.13 Measurement of heat pipe simulator

由于线缆、热管在拉伸、压缩过程中会产生形变，因此不同长度的拉伸压缩刚度不是线性变化的。

3.3 试验结果分析

1）扫频测试

以x轴转动方向为例，对有无线缆、热管附加连接这2 种工况下的物理系统进行扫频测试分析，利用ASP 平台作动器产生x轴转动方向的扫频力矩，扫频频率范围取0.1～100 Hz，利用测微敏感器测量载荷角速度，并通过快速傅里叶变换（Fast Fourier Transformation，FFT）变换获取频域响应曲线。开环系统动力学辨识曲线如图14 所示。

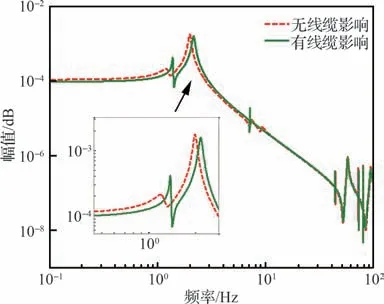
图14 开环系统x 轴转动辨识模型对比Fig.14 Comparison of open-loop x rotation for identifi‐cation model

从辨识曲线图14 可以看出，线缆、热管模拟件等附加连接略微提升了系统的固有频率，提升约0.17 Hz；降低了开环系统在低频阶段的增益，降低约2 dB。试验实测结果与2.2 节中的理论分析结论一致。

值得注意的是，理论分析的固有频率与试验实测值有一定差别，实测值比理论分析值略高。其中，理论模型无附加刚度转动刚体固有频率为1.28 Hz、1.48 Hz，无附加刚度模型试验实测值分别约为1.25 Hz、2 Hz，主要原因如下：①试验载荷与理论模型存在一定差异；② 低频悬吊对系统产生附加刚度。

系统x轴转动稳定性分析如图15 所示。线缆、热管等附加连接略微降低了系统的幅频裕度，降低约0.4 dB，对系统稳定性的影响较小。试验实测结果与2.3 节中理论分析结论保持一致。

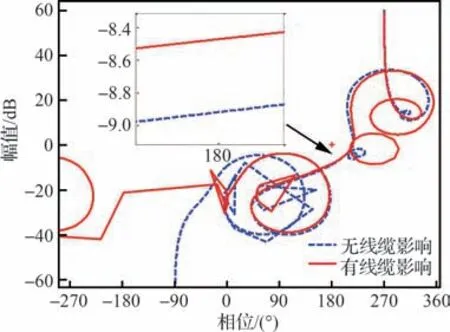
图15 辨识模型x 轴转动方向稳定性分析Fig.15 Stability analysis of x rotation channel for iden‐tification model

2）姿态指向控制试验

同样以x轴转动方向为例，利用ASP 对载荷x轴姿态进行姿态指向控制。载荷x轴姿态由初始状态0″ 调节至100″，如图16 所示。

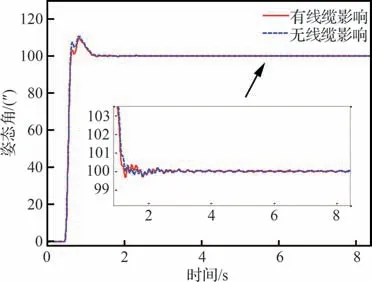
图16 x 轴转动方向姿态指向试验对比Fig.16 Comparison of x rotation attitude active point‐ing experiment

试验测试结果表明，采用试验中线缆、热管的连接布局方式对载荷姿态指向控制调节时间与控制精度的影响均不明显，试验中的装配布局可供整星参考。

4 自适应预设性能控制器

附加刚度的存在不仅影响了ASP 的控制性能，还增加了对载荷的扰动传递路径，即卫星平台对载荷的扰动不仅通过ASP 传递，还可以通过附加连接的线缆热管传递；除此之外，附加刚度放大了载荷与卫星平台之间的耦合现象，进一步影响了载荷的动态响应特性。针对以上问题，本文提出了一种自适应预设性能非线性控制器，实现了存在附加连接下载荷的敏捷机动、扰动抑制与精确指向。

4.1 控制器设计

1）性能函数

定义系统性能的约束函数为［27］

式中：ρ0表示性能函数初始值；ρ∞为稳态值；k是性能函数衰减速率。

利用性能函数式（17）来约束状态误差eg（t）

其中：σ∈[0，1]。

2）误差变换［27］

为了控制跟踪误差处在性能函数的界限中，定义一个严格单调递增的函数S(ε)，其中ε∈（−∞，+∞）

根据S(ε)的性质可知［28］，总存在一个变化误差ε可以将性能约束转化为

由于S(ε)∈(−1，1)，所以这时的S(ε)充当了性能函数σ的作用，利用反变换得到变换误差ε

由于变换误差ε的定义域为ε∈(−∞，+∞)，因此只要使得变化误差ε有界，跟踪误差eg(t)就在约束范围内。因此与其他控制方法相比，预设性能控制器对模型参数的依赖性更小，令

定义滑动变量

对变量s求导

3）控制器设计

根据式（2）载荷动力学方程设计控制器

综合扰动包括：转动平动耦合扰动、高阶非线性项和卫星平台扰动等；r=diag{r1，r2，r3}，K为正数，令v=[v1v2v3]T，其中

设计自适应律为

其中：α为正数。

4.2 稳定性证明

设计李雅普诺夫函数

假设1综合扰动d慢时变，为零或小量，可以忽略。

因此式（31）变为

由式（32）得出，系统渐进稳定，跟踪误差eg在约束范围内。

假设2综合扰动d快时变。

式（31）变为

可以设计较大的参数K与α，使式（31）收敛到0 的邻域内，因此s一致最终有界（Uniform ul‐timate boundedness），由此可知ε有界，因此误差eg仍在约束范围内［29］。

4.3 数值仿真分析

利用4.1 节设计的控制器对载荷姿态进行控制，卫星平台仍然使用式（12）中的比例-积分-微分（Proportion Integration Differentiation，PID）进行控制。仿真中，目标姿态角[20 20 20]T（°），期望轨迹采用5 次多项式进行规划，最大角速度不超过1（°）/s，最大角加速度不超过1（°）/s2。

在实际试验中发现，卫星平台对载荷的高频扰动主要由平台安装的高速转动陀螺产生，陀螺转动速度9 600 r/min，因此扰动频率约为160 Hz（约1 000 rad/s），设置卫星平台扰动力矩Mds=[Mdsx Mdsy Mdsz]TN⋅m 如下所示

由图17～图19 载荷姿态跟踪误差可以看出，本文提出的自适应预设性能控制器可使载荷姿态误差严格保持在预设的性能函数界内，具有良好的动态跟踪性能。

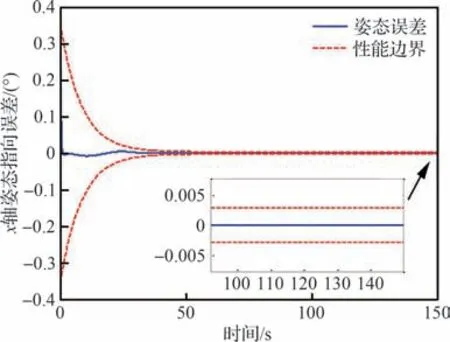
图17 载荷x 轴姿态指向误差Fig.17 Payload attitude pointing error of axis x

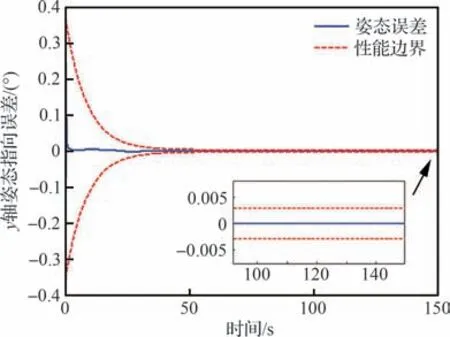
图18 载荷y 轴姿态指向误差Fig.18 Payload attitude error of axis y

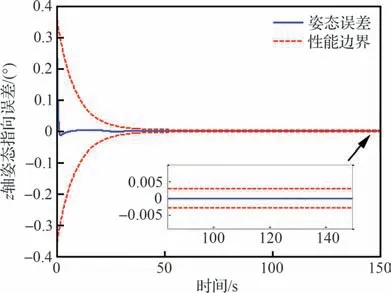
图19 载荷z 轴姿态指向误差Fig.19 Payload attitude pointing error of axis z

如图20 所示，以载荷x轴为例对比分析了自适应预设性能控制与传统PID 控制对载荷的控制效果。从仿真曲线中可以看出，本文提出的自适应预设性能控制方法有效补偿了载荷与平台动力学之间存在的非线性耦合，与传统的PID 控制相比，使载荷具有更快的稳定跟踪能力，显著提升了载荷的姿态指向精度。

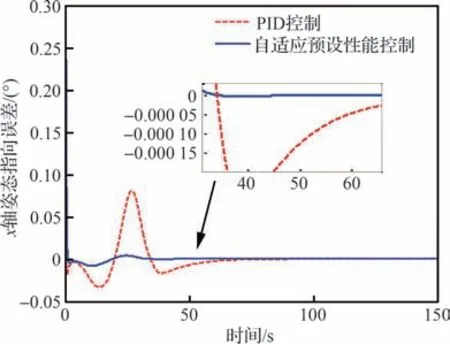
图20 载荷x 轴姿态指向误差对比Fig.20 Comparison of payload attitude pointing errors of axis x

平台、载荷x轴姿态轨迹跟踪曲线如图21 所示。从仿真结果图中可以看出，采用本文提出的控制方法依然使载荷较平台拥有更快的机动速度、更稳定的跟踪能力与更高的指向精度。

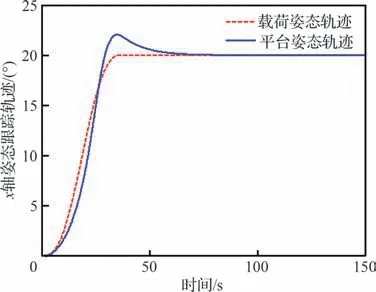
图21 载荷、平台x 轴姿态跟踪轨迹Fig.21 Payload and platform attitude trajectory of axis x

除此之外，从图20 中20～50 s 时间段内发现，采取本文提出的控制方法明显减小了载荷的跟踪误差，综合图21 分析可知：本文提出的自适应预设性能控制补偿了平台对载荷的耦合扰动，进一步提升了载荷的快速机动、稳定跟踪与高精度姿态指向能力。

2 种控制器性能对比如表7 所示，从表中可以看出，本文提出的自适应预设性能控制器控制性能明显优于PID 控制，进一步验证了本文所设计控制器的优越性。

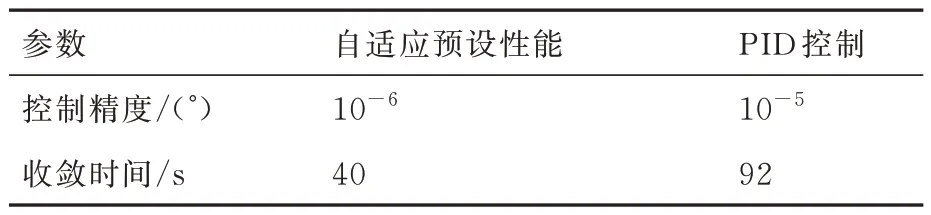
表7 2 种控制器性能对比Table 7 Comparison of two controllers

5 结论

针对存在附加连接情况下的超精超稳超敏捷卫星系统，通过理论分析与试验验证的方式，分析研究了线缆、热管连接对系统控制效果的影响，获得了线缆、热管附加连接在一定范围内的刚度参数，试验中线缆、热管的安装布局对实际型号有较高的参考价值。除此之外，本文还设计了自适应预设性能非线性控制器，解决了附加刚度存在情况下的动力学耦合问题。具体结论如下：

1）建立了超精超稳超敏捷卫星多级动力学模型与附加刚度力学等效模型，仿真分析了附加刚度对系统控制性能产生的影响，为后续试验的设计与测试提供了理论支持。

2）通过试验获得了线缆、热管附加连接在一定范围内的拉伸、压缩刚度，掌握了实际工程应用中附加连接刚度的变化范围，对理论模型进行了修正。

3）试验结果与理论分析吻合性较好，附加连接会提升系统固有频率、降低系统稳定裕度，但总体对系统影响有限。采取试验中的线缆、热管装配布局对系统稳定裕度、姿态指向调节时间与控制精度影响均不明显，试验中的装配布局可供整星参考。

4）提出了一种自适应预设性能非线性控制器，解决了附加刚度存在下的载荷、平台严重耦合与振动抑制问题，进一步提升了载荷的敏捷机动、稳定跟踪与高精度姿态指向能力。