可压缩流动模拟的多重网格-扰动域推进方法
胡姝瑶,蒋崇文,李椿萱
北京航空航天大学 航空科学与工程学院 国家计算流体力学实验室,北京 100191
多重网格方法是一种在粗、细网格间循环求解控制方程的加速收敛技术,是飞行器绕流数值模拟加速中广泛使用的手段之一[1]。多重网格法的加速原理有2 方面:一是粗网格以更大的时间步长推进求解,从而带动细网格更快达到收敛态;二是粗、细网格间的循环求解有助于衰减阻碍细网格收敛的高频误差,从而使细网格的整体误差能更快地衰减[2]。
多重网格方法起源于椭圆型方程的数值计算,并已被证明对于椭圆型问题是一种最优化的数值方法[3]。Ni[4]最先将多重网格方法推广至双曲型的非定常Euler 方程,建立了定常可压缩流动的显式多重网格求解器。Jameson 等[5]将隐式时间格式引入多重网格方法,进一步提高了Euler 方程的求解效率。Yadlin 等[6]将隐式多重网格方法推广至多块网格,验证了多重网格内边界的处理方式。随后,该方法又被推广至黏性[7]、高超声速[8]、化学反应[9]等复杂流动的模拟,应用于螺旋桨滑流[1]、外挂物投放[10]、压气机内流[11]、喷流干扰[12]等工程问题的研究中。
当前,多重网格方法[13]已成功应用于各类流动的研究中,可实现数十倍的收敛速率增长。不过,无论是在细网格还是粗网格上,现有多重网格方法在每个迭代步内均必须对所有网格单元更新求解。这一全局更新的求解方式虽便于实现,却未考虑流场扰动传播与数值迭代收敛的特征,可能导致大量无效计算,限制计算效率。
针对传统全局更新求解方式存在无效计算的问题,本文作者前期工作[14-17]提出了扰动域推进方法,以提升可压缩流动数值模拟的计算效率。扰动域推进方法的加速原理是采用随扰动传播而增大、随求解收敛而缩小的动态计算域,实现了仅在未收敛的受扰区域求解,N-S 方程、Euler 方程动态分区耦合求解的局部更新求解方式。通过有效避免传统方法中的无效计算,扰动域推进方法可同时显著降低可压缩流动数值模拟的单步计算量和存储需求。对于典型亚声速流动计算时间节省可达54.0%,对于典型超声速流动时间节省可达74.5%[17]。
本文将在扰动域推进方法的计算框架下融入多重网格方法,着重建立粗网格上动态计算域的演化逻辑,设计对结构网格更为普适的新型粗网格生成策略,提出多重网格-扰动域推进方法,并通过典型算例验证多重网格、扰动域推进2 类加速技术的耦合加速效果。
1 控制方程及数值方法
1.1 控制方程
扰动域推进方法采用了有黏、无黏流动的动态分区计算,其中模拟无黏、层流和湍流的控制方程分别为Euler 方程、N-S 方程和RANS 方程。若忽略体积力与热源,3 类方程可统一描述为
式中:t为时间;Ω表示控制体,∂Ω为其边界;dΩ、dS分别为体积分及面积分的微元。在笛卡尔坐标系(x1,x2,x3)下,守恒变量W、对流通量Fc、黏性通量Fv以及源项Q可表示为
式中:ρ、P、T、E和H分别表示密度、压强、温度、比总能和比总焓;λ为热传导系数;μ为动力黏性系数;ui为速度分量;τij为分子剪应力张量;δij为Kronecker 函数(i,j=1,2,3);下标“T”表示湍流模型。
对于无黏流动,去除式(1)中包含μ以及湍流相关的项,包括Fv、Q、WT、Fc,T,式(1)即可退化为Euler 方程。对于层流流动,去除湍流相关项,μ设为满足Sutherland 公式的分子黏性系数μL,式(1)即为N-S 方程。对于湍流流动,保留所有项,μ设为分子黏性与湍流涡黏性系数之和,即μ=μL+μT,式(1)即为满足Boussinesq 涡黏性假设、省略了Reynolds 平均与Favre 平均符号的RANS 方程。
1.2 定常可压缩流动的有限体积方法
本文方法将基于结构贴体网格的有限体积法实现。假设式(1)中,W、Q在一个网格单元内恒定,通量的曲面积分可由网格单元面的通量加和近似,则式(1)可离散为
式中:残差R可表示为
其中:|Ω|表示网格单元的体积;Nf为网格单元的面数;nm和ΔSm分别为网格单元第m个面的单位外法向和面积(1≤m≤Nf)。
对于定常可压缩流动,数值模拟旨在通过迭代求解式(3),确定出满足dW/dt=0的W。其中,近似式(3)等号右端项与左端项的步骤分别称为残差估计和时间积分。残差估计以上一迭代步的守恒量W(n−1)为输入,根据式(4),利用空间离散格式近似当前迭代步的残差R(n)。时间积分则以R(n)为输入,利用时间离散格式估计当前迭代步的守恒量更新量ΔW(n),并更新守恒量,即W(n)=W(n−1)+ΔW(n)。在每一迭代步通过所有单元的||ΔW(n)||2判断收敛情况,若所有单元的最大值小于给定的收敛阈值εc,即||ΔW(n)||2,max<εc,则停止计算。
传统方法中,残差估计与时间积分要在预设的计算域内对所有单元执行,两者的耗时约占总计算时间的99%[14],十分耗时。扰动域推进方法正是旨在减少这2 个步骤的计算量。为避免混淆,下文中将同时求解所有单元的方法称为传统全局更新方法,其所使用的静态计算域称为预设计算域。
1.3 多重网格方法
多重网格方法需在一层细网格和若干层粗网格上,按指定规律循环求解式(3)。对于结构网格,常用的粗网格生成方法是将细网格沿网格方向稀疏一倍[2]。常用的多重网格循环有V 型、W 型等,其均由基础循环组成[18]。基础循环包括以下3 步:
1)将细网格的守恒量与残差插值到粗网格。
在细网格求解更新后,将粗网格所包含细网格的体积加权平均守恒量作为粗网格的守恒量初值,即
式中:Nc为粗网格所含细网格的个数;下标h、2h分别表示细网格和其稀疏一倍所得粗网格。粗网格的体积|Ω|2h可表示为
2)在粗网格上迭代求解控制方程。
由于粗网格的数值精度不会影响细网格,为提高效率,多重网格法通常只采用一阶迎风格式求解粗网格上的对流通量,也不在粗网格上求解湍流模型方程。为将细网格精度传给粗网格,以源项形式在控制方程中引入考虑粗、细网格间精度差异的强迫函数(QF)2h,可定义为
粗网格所采用的时间推进格式与细网格保持一致。粗网格上的迭代步数可任意给定,文献[13]指出当以LU-SGS 格式推进求解时在粗网格上迭代2 步可使效率最佳。
3)将粗网格的守恒量修正量插值回细网格。
定义粗网格第n次迭代所得守恒量与粗网格的守恒量初值之差为粗网格的守恒量修正量,即
则细网格的新解可表示为
当粗网格多于1 层且采用迎风格式求解对流通量时,文献[18]推荐粗网格通过式(11)获得新解后,先迭代一步再将其修正量插值给更密网格以获得最佳的多重网格性能。
1.4 扰动域推进方法
本文作者的前期工作表明,定常可压缩流动的求解过程具有4 点特征[15]:①流场的数值扰动始于定常控制方程未满足之处;②扰动向周围逐渐传播,尚未受扰区域仍保持初始值;③整个预设计算域并非同时收敛,位于上游及远离壁面的区域会先收敛;④无论流动是否分离,黏性效应仅在有限区域起主导作用。因此,全局更新方法在未受扰动和已收敛区域内的求解对数值迭代不仅没有积极贡献,反而可能引入更多数值误差,延迟迭代收敛。
为利用这4 点特征提高计算效率,本文提出了采用动态计算域的扰动域推进方法。该方法的特征如下:①定义了对流、黏性2 类动态计算域,且黏性动态域⊆对流动态域⊆预设计算域;②初始动态计算域包括壁面边界毗邻单元或不满足来流条件的单元;③动态计算域随数值扰动传播而增大,随求解收敛而缩小;④残差估计与时间积分仅在对流动态域中执行,并仅在黏性动态域中考虑式(4)中的黏性项。
图1 将扰动域推进方法与全局更新方法的求解流程进行了对比。图中白色框为2 种方法的共有步骤,黄色框则为扰动域推进方法的特有步骤。对于全局更新方法,白色框步骤将全在预设计算域中执行。对于扰动域推进方法,红色虚线框中的步骤则在对流动态域中执行,而绿色虚线框的步骤则仅在黏性动态域中执行。
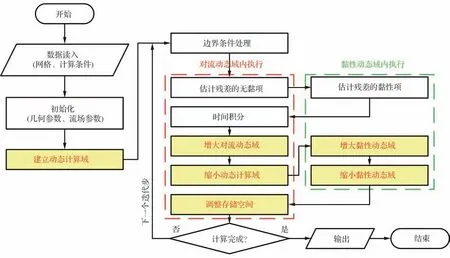
图1 扰动域推进方法与全局更新方法的流程对比Fig.1 Comparison of flow charts between Disturbance Region Update Method(DRUM)and Global-Update Method(GUM)
扰动域推进方法的特有步骤可分为3 类:①迭代求解前,建立动态计算域;②在每一个迭代步中,更新动态计算域,依次执行增大对流动态域、缩小对流动态域、增大黏性动态域和缩小黏性动态域4 个子步;③根据对流动态域,调整存储空间。前2 类特有步骤旨在确保扰动域推进方法能够消除全局更新方法中的无效计算,第3 类则使得扰动域推进方法可在提高计算效率的同时减少存储空间占用。为便于阅读,下文将简要介绍动态计算域建立与更新算法的原理,算法的数学表达如表1 所示。算法的具体推导、经验参数取值的讨论详见文献[14-17]。

表1 扰动域推进方法动态计算域更新算法Table 1 Update algorithms of dynamic computational domains in DRUM
1.4.1 建立动态计算域
根据流场初始化方式的不同,对流、黏性动态计算域的建立分为2 种情况:①当根据来流条件初始化时,对流、黏性2 类动态域依据壁面边界建立,分别取紧邻壁面的10 层和1 层单元作为初始单元;②当根据给定流场初始化时,对流动态域包含与来流条件不符的单元,黏性动态域包含对流动态域中的黏性主导单元。
1.4.2 增大对流动态域
遍历对流动态域的边界单元,对每一边界单元执行如下2 个子步:①判断是否为受扰单元;②若是受扰单元,将其可能受到扰动的相邻单元加入对流动态域;亚声速流动中,可能受到扰动的是所有相邻单元;而超声速流动中,则是位于下游的单元。
1.4.3 缩小对流动态域
遍历对流动态域的边界单元,对每一边界单元判断如下4 个条件:①求解已收敛且周围不存在新增受扰单元;②位于对流动态域的最上游;③对于亚声速流动,不再影响对流动态域中其他单元的求解;④不再受对流动态域中其他单元的影响。若上述4 个条件均满足,则将该单元从对流动态域中移除,该单元的紧邻单元将成为对流动态域新的边界单元,继续判断。由于黏性动态域⊆对流动态域,因此若该单元同时位于黏性动态域中,将其也从黏性动态域中移除。
对于超声速流动,由于流动速度明显大于声速,数值求解过程具有“上游先于下游收敛”的规律。因此,对流动态域的更新须保持“从上游向下游缩小”,即严格满足条件②。而对于亚声速可压缩流动,由于流动速度与声速量级接近并且预设计算域较大,数值求解过程呈现“远场先于近壁区收敛”的规律。因此,条件②被适当放宽以提高计算效率,但增加了条件③以避免降低计算精度。
1.4.4 增大黏性动态域
遍历黏性动态域的边界单元,对每一边界单元执行如下2 个子步:①判断是否受黏性效应主导;②若受黏性效应主导,则将其所有紧邻单元加入黏性动态域。
1.4.5 缩小黏性动态域
遍历黏性动态域的边界单元,对每一边界单元判断如下2 个条件:①位于黏性动态域的最上游;②不再受黏性效应主导。若上述2 个条件均满足,则将该单元从黏性动态域中移除,该单元的紧邻单元将成为黏性动态域新的边界单元,继续判断。
2 多重网格-扰动域推进方法
为整合多重网格、扰动域推进2 类方法的加速优势,本文提出多重网格-扰动域推进方法。其求解流程如图2 所示,有别于扰动域推进方法的步骤由绿色框标出。由图可知,无论是在细网格还是粗网格上,扰动域推进方法依旧在对流动态域内求解控制方程,仅在黏性动态域内考虑黏性效应。动态计算域更新算法的运算仅在细网格上执行,而粗网格的动态计算域则根据粗、细网格间的对应关系生成。本节将对多重网格-扰动域推进方法的特有步骤进行介绍,包括粗网格初始化、建立动态计算域、增大对流动态域、调整存储空间、动态计算域中粗、细网格间的插值等。未提及的步骤与扰动域推进方法完全相同。
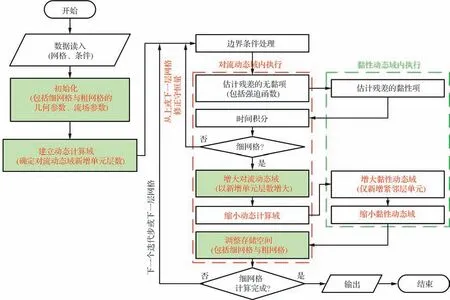
图2 多重网格-扰动域推进方法流程图Fig.2 Flow chart of DRUM with multigrid
2.1 粗网格初始化
在读入细网格的网格格点坐标、边界条件和计算参数后,需首先对粗、细网格的几何参数与流场参数进行初始化,为后续控制方程的迭代计算提供参数与初值。粗网格初始化的关键有2 点:一是计算粗网格几何参数与流场参数的方法;二是粗网格与细网格间的对应关系。
数值实验表明,由于存在强迫函数,无论是依据粗网格的顶点坐标精确计算其体积、面向量、格心等几何参数,还是通过细网格的几何参数近似,均对多重网格的加速效果没有影响。本文采用通过细网格估计粗网格几何参数的方式,即采用式(6)计算粗网格单元体积,格心坐标、面向量均采用细网格单元值的加权平均值。
在迭代求解中,由于仅在对流动态域中进行多重网格循环,因此多重网格-扰动域推进法在流场初始化时就必须采用式(5)为粗网格的所有单元赋守恒量初值。
对于一个结构网格,文献[2]采用沿一网格方向将一对紧邻单元合二为一的方式生成粗网格,即对于一个单元数为2a×2b×2c的网格块,第1 层粗网格的单元数为2a−1×2b−1×2c−1。若目标粗网格层数是L,则网格单元数需满足a≥L,b≥L,c≥L;若不满足,则会出现单个无法合并单元,影响多重网格方法的使用和效果。
为消除多重网格使用对单元数的限制,本文提出一种新型粗网格生成策略。令m(0)表示读入的网格在某一网格方向上的单元数,则第i层粗网格在网格方向的单元数可表示为
式中:mod(∙)代表取模。第i层网格的单元I(i)对应于第i+1 层网格单元的标号为
图3 以L=2、m(0)=11 的情况为例,示意了本文所提粗网格生成策略的特点。考虑到细网格是网格尺度最小的网格层,相比其他层粗网格,将细网格单元合二为一或合三为一的尺度差异最小,更有助于生成分布均匀的粗网格。因此,当细网格沿一网格方向的单元数无法整除2L时,本文方法仅在第1 层粗网格出现合并3 个紧邻单元作为1 个粗网格的情况,如图3 所示。

图3 粗网格生成策略示意图Fig.3 Schematic of generation of coarse grids
2.2 建立粗、细网格上的动态计算域
在开始控制方程的迭代求解前,还需建立动态计算域以确定第1 步参与计算的范围。细网格上动态计算域的建立方法与1.4.1 节所述的扰动域推进方法完全相同。粗网格的动态计算域根据细网格的生成。若某一细网格单元包含于某类动态域中,则对应于该细网格单元的粗网格单元也被加入粗网格相应的动态域中。在迭代求解中,当细网格的动态计算域更新完毕,粗网格的动态计算域也采用同一方式更新。
2.3 增大粗、细网格上的对流动态域
在完成控制方程一个迭代步的求解后,需根据更新后的流场对动态计算域进行更新。这其中,由于对流动态域的范围直接影响求解的收敛性,因此需首先执行增大对流动态域,将可能需要计算的单元加入对流动态域。在多重网格-扰动域推进方法中,增大对流动态域的判断算法仅在细网格执行。
细网格上对流动态域的增大算法与1.4.2 节所述的扰动域推进方法完全相同,对每个对流动态域边界单元均执行2 个子步:①判断是否为受扰单元;②若是受扰单元,将其可能受到扰动的相邻单元加入对流动态域。
对于子步②,扰动域推进方法忽略了时间格式对扰动传播速度的影响,至多允许一层紧邻单元加入对流动态域。不过,与多重网格法结合后,数值扰动在一个时间步内可通过最粗层网格传向更远的地方。为避免因对流动态域增长缓慢而影响收敛速率,在多重网格-扰动域推进方法中,细网格的对流动态域不再每次仅新增受扰单元的一层紧邻单元,而是依据多重网格的层数调整对流动态域的新增单元层数。
考虑到粗网格是通过稀疏细网格得到的,若要求最粗一层网格每次仅新增受扰单元的紧邻一层单元,则在细网格上对流动态域的新增单元层数La,c可估计为
式中:当不采用多重网格时,L取0,则式(15)对应于扰动域推进方法的情况。
为提高动态计算域更新运算的效率,式(15)并未考虑第1 层粗网格可能出现将细网格单元合三为一的情况。数值实验表明,这一简化不会对多重网格-扰动域推进方法的收敛性产生影响。一方面,对流动态域的增大十分迅速,迭代求解不会因计算域在一个迭代步中不足而立即发散;另一方面,初始对流动态域留有余量。初始对流动态域中包含了10 层紧邻壁面的细网格单元或所有与来流条件不符的单元,这2 种情况中的对流动态域都大于会导致求解发散的最小求解范围。
从加速效果的角度来看,式(15)估计的是在下一个迭代步中细网格上可能受到扰动的单元,其也可能会将过多单元加入对流动态域。不过,由于对流动态域缩小步骤会在下一个迭代步及时将未受扰动单元从对流动态域中移除,因此即使式(15)导致对流动态域偏大,也不会对多重网格-扰动域推进方法的计算效率产生明显影响。
2.4 调整存储空间
扰动域推进方法将数据分为固有信息和迭代相关信息2 类。固有信息是指在输出时必须包含的几何信息和流场信息,如网格坐标、守恒量等。迭代相关信息是指与迭代求解方法相关的信息,如守恒量更新量、当地时间步长、上一迭代步的守恒量等[14]。对于固有信息,仍与传统全局更新法一样,采用静态数组存储。对于迭代相关信息,则采用动态数据结构仅存储对流动态域中单元的信息,以节省内存需求。
多重网格-扰动域推进方法在粗网格上也沿用这种数据存储方式。在每个迭代步完成动态计算域的更新后,便根据对流动态域的范围调整粗、细网格上迭代相关信息的存储空间,从而同时节省粗、细网格上的内存需求。
2.5 动态计算域中粗、细网格间的插值
各层网格间依靠守恒量、残差的相互插值建立联系。当从第i层网格进入第i+1 层时,需采用式(5)为第i+1 层单元的守恒量赋初值,采用式(7)确定第i+1 层单元的插值残差。对于守恒量初值,无需区分所对应第i层单元是否位于对流动态域中,仍以所有对应单元的守恒量体积加权平均值作为第i+1 层单元的初值。对于插值残差,未包含于第i层对流动态域中的细网格单元的残差取0。当从第i+1 层网格进入第i层时,需采用式(10)计算第i+1 层单元的守恒量修正量。此外,未包含于第i+1 层对流动态域中的单元的δW2h取0。
3 算例验证
本文的多重网格-扰动域推进方法在Win‐dows 10 系统下以Fortran 2003 语言实现。粗、细网格上的时间离散均采用LU-SGS 隐式格式[19]。细网格上的对流离散格式为熵修正的Roe 格式[20],重构格式为结合van Albada 限制器的MUSCL 插值[2]。细网格上的湍流模型选用压缩修正的S-A 模型[21]。粗网格上,对流离散采用一阶迎风格式,并且不在粗网格上求解湍流模型方程。使用1~4 层粗网格:1 层粗网格情况即为执行一次基础循环,2~4 层粗网格时采用W 型循环。计算迭代的收敛阈值εc取10−7,动态计算域更新算法中参数的取值如表1 所示。多重网格方法在亚声速流动中具有更优秀的加速效果,因此选取2 个典型亚声速问题进行验证。
3.1 跨声速无黏NACA0012 翼型
本算例考虑了以马赫数0.85、1°迎角流经NACA0012 翼型的跨声速无黏流动。网格采用C 型拓扑,外边界大于20 倍的翼型弦长以消除有限计算域的影响,网格量为468×120。本算例为无黏流动问题,多重网格-扰动域推进方法中仅存在对流动态域。图4 展示了3 层粗网格加速时多重网格-扰动域推进方法中对流动态域的演化过程。图中,ηc表示对流动态域与预设计算域的网格量之比;Nmax表示达到收敛态的迭代总步数。
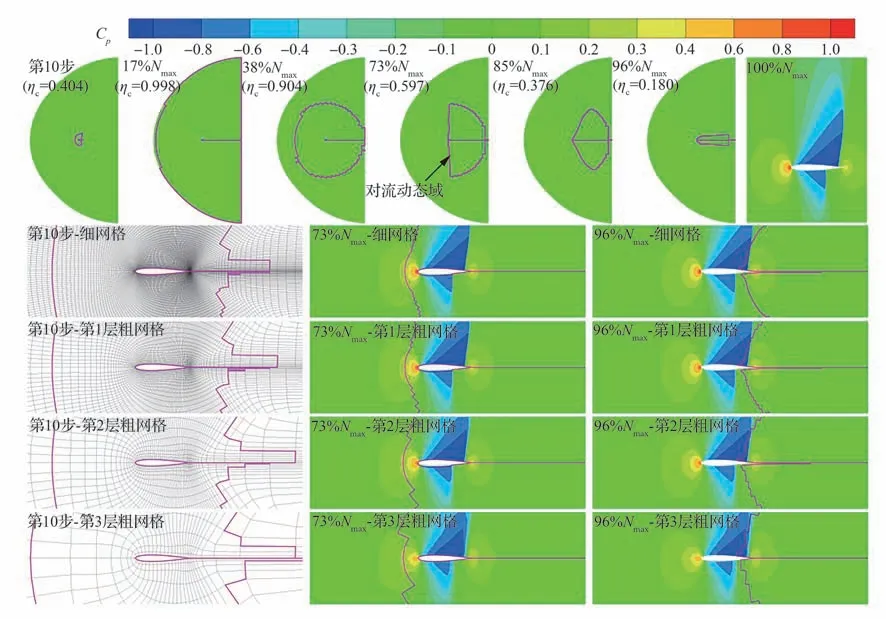
图4 多重网格-扰动域推进方法的跨声速无黏NACA0012 翼型求解过程(3 层粗网格)Fig.4 Solutions of transonic inviscid NACA0012 airfoil by DRUM with three coarse grids
由图4 的第1 行可知,流场以来流条件初始化,因此对流动态域依据壁面边界建立。在求解初期,扰动逐渐从壁面边界向远场边界传播,对流动态域也随之增大,如第10 步情况所示。采用3 层粗网格后,对流动态域每次新增8 层相邻单元。因此,仅用10 步就将约40%的预设计算域单元纳入对流动态域中。亚声速流动中,扰动可随声波传向四周;相应地,对流动态域会随扰动扩展至整个预设计算域。
随着时间推进,远场附近单元先达到定常态,对流动态域的缩小起始于最上游远场区域,如17%Nmax的情况所示。随后,对流动态域逐渐向壁面缩小,如38%Nmax的情况所示。激波附近存在的流动特性大梯度会导致求解更难以达到定常态。因此,在73%Nmax~96%Nmax的情况中,对流动态域的缩小被翼型上、下两道激波所阻挡。在计算结束时,即100%Nmax的情况,对流动态域消失,翼型上、下表面的两道激波均被清晰捕捉。
图4 的下半子图对比了不同网格层上对流动态域的区别。由于粗网格上的动态域是依据细网格上的生成,因此粗网格上对流动态域的形状与细网格上的保持一致。但随着网格粗化,对流动态域所包含的范围会有所扩大。这是由于,即使某一粗网格单元所对应的多个细网格单元中,仅有一个包含在细网格上的动态域中,该粗网格单元仍会被纳入该层粗网格的动态域。
本算例中,翼型的上、下表面均会产生激波。从图4 第1 行中100%Nmax情况的局部放大图可以看出,翼型上、下表面的两道激波均能被清晰捕捉;受1°迎角的影响,上表面激波更靠近后缘,强度也较高。图5 将采用3 层粗网格的多重网格-扰动域推进方法所得壁面压力分布与传统多重网格方法的、文献[22-23]的结果进行了对比。对比表明,本文方法与传统多重网格方法的结果完全重合,本文方法提供的数值结果与文献[22-23]的数值、实验结果也能很好吻合。

图5 NACA0012 翼型压力系数分布对比Fig.5 Comparison of pressure coefficient distributions on NACA0012 airfoil
表2 将本文采用3 层粗网格所得翼型表面气动力系数与文献[22]的结果进行了对比。其中,CL、CD分别表示升力系数和阻力系数;ΔCL/CL、ΔCD/CD分别为本文所得升力系数和阻力系数与文献[22]结果的相对偏差。由对比可知,本文数值结果与文献[22]的气动力偏差均在1.92%以内。因此,本文所使用的传统多重网格方法和多重网格-扰动域推进方法能够提供正确的无黏流动数值解。
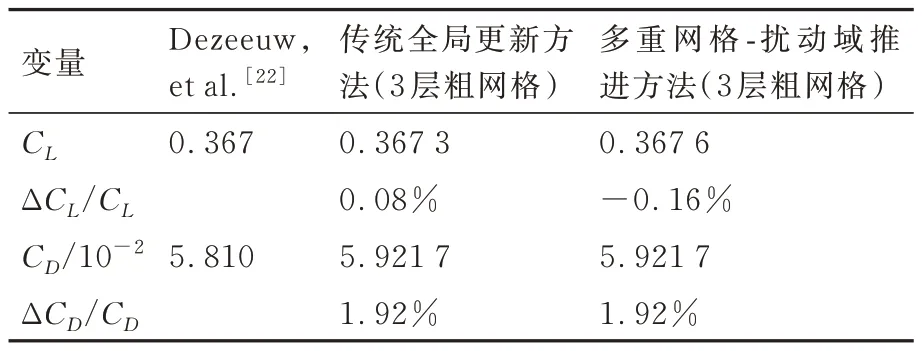
表2 NACA0012 翼型的气动力对比Table 2 Comparison of forces on NACA0012 airfoil
图6 对比了不同粗网格层数下对流动态域的网格量变化。由图可知,所有采用多重网格情况的ηc增长率均会大于未采用多重网格的情况,且粗网格层数越多,ηc增长率越快。这一现象有2 方面原因:其一,多重网格-扰动域推进方法要求对流动态域的新增单元层数与粗网格层数成正比;其二,粗、细网格间的循环迭代能加速扰动的传播,也会促使对流动态域增长更快。
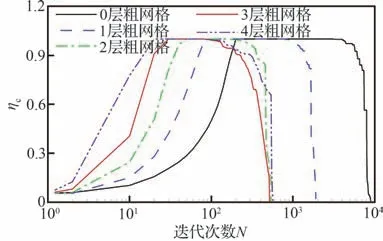
图6 NACA0012 翼型问题对流动态域网格量变化曲线Fig.6 Evolution of number of cells in advective dy‐namic computational domain for NACA0012 airfoil
图7(a)和图7(b)分别展示了本算例中传统全局更新方法和扰动域推进方法采用0~4 层粗网格求解时的收敛曲线。由图7(a)中不同粗网格层数的收敛曲线对比可知,多重网格方法有助于消除求解后期收敛曲线的振荡,从而大幅降低总迭代步数。观察图7(b)中的收敛曲线可知,由于动态计算域的缩小,扰动域推进方法在求解后期也可起到与多重网格相同的效果,因此也同样有大幅降低总迭代步数的效果。
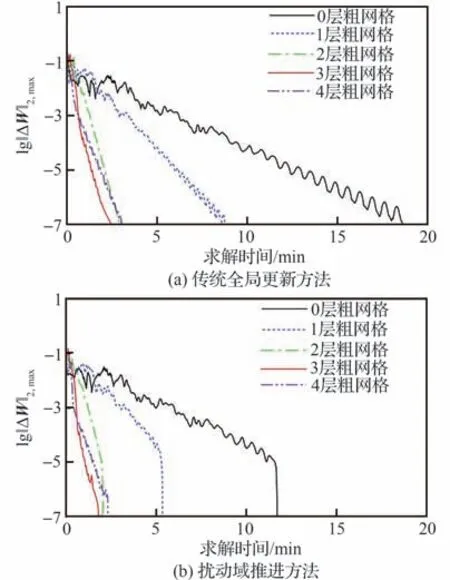
图7 NACA0012 翼型问题收敛曲线Fig.7 Convergence histories of NACA0012 airfoil
表3 对比了本算例中采用不同层粗网格扰动域推进方法的加速效果与求解精度。其中,扰动域推进时间节省是指相同粗网格层数下多重网格-扰动域推进方法相对于传统全局更新方法的计算总耗时节省量;求解精度是指相同粗网格层数下多重网格-扰动域推进方法相对于传统全局更新方法的升力、阻力系数最大偏差。

表3 NACA0012 翼型的扰动域推进效果Table 3 Acceleration effects stemming of DRUM for NACA0012 airfoil
得益于同时降低细网格与粗网格上的计算量并减少达到收敛所需的迭代步数,多重网格-扰动域推进方法在传统多重网格方法加速的基础上还可再提升25.0%~39.9%的计算效率。对比不同粗网格层数的情况可知,随着粗网格层数的增加,多重网格-扰动域推进方法的时间节省量会逐渐降低,但求解精度也逐渐提升。这一现象的主要原因在于,多重网格和扰动域推进2 种方法都有在求解后期消除残差振荡的效果,如图7所示;而当粗网格层数>1 时,传统多重网格方法已可完全消除残差振荡现象;此时,扰动域推进方法的迭代步数节省量显著减小,其加速效果主要来源于通过对流动态域的缩小同时降低细网格与粗网格上的计算量。因此,扰动域推进时间节省量随着粗网格层数的增加而降低。
此外,表3 的效率与精度结果对应于动态计算域更新中阈值恒定的情况。多重网格-扰动域推进方法的计算效率还可通过缩小对流删除阈值εd、增大上游容差角θd等阈值来提升。
表4 给出了多重网格-扰动域推进方法相比于未使用多重网格的传统全局更新方法的时间节省量。本算例中,采用3 层粗网格的情况获得了最优的加速效果,可节省90.8%的计算时间。此外,本算例网格在I方向的单元数为468,无法整除23。因此,采用3 层粗网格情况获得最优加速效果也证明了本文所提出的新型粗网格生成策略切实可行,可有效提高多重网格-扰动域推进方法的适用性。

表4 NACA0012 翼型的总加速效果Table 4 Total acceleration effects of DRUM for NACA0012 airfoil
综上所述,本算例验证了多重网格-扰动域推进方法对亚声速无黏流动模拟的适用性。得益于同时降低细、粗网格的计算量并减少总迭代步数,多重网格-扰动域推进方法相比于传统多重网格方法可展现出更为显著的加速效果。
3.2 跨声速湍流RAE2822 翼型
本算例考虑了跨声速RAE2822 翼型风洞试验[24]的第6 种状态,即来流马赫数为0.729,雷诺数为6.5×106,迎角为2.31°。使用NASA 网站所发布的网格进行数值模拟,网格量为368×64。本算例为湍流流动,多重网格-扰动域推进方法中包含对流、黏性2 类动态计算域。图8 展示了采用3 层粗网格时求解跨声速湍流RAE2822 翼型中动态域的演化过程;其中,ηv表示黏性动态域与预设计算域的网格量之比。
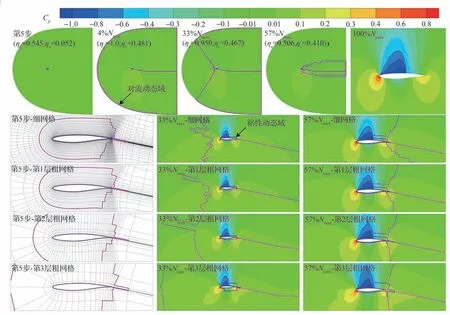
图8 多重网格-扰动域推进方法的跨声速湍流RAE2822 翼型求解过程(3 层粗网格)Fig.8 Solutions of transonic turbulent RAE2822 airfoil by DRUM with three coarse grids
由图8 的第1 行可知,初始流场设定为具有来流状态的均匀流场,因此对流、黏性2 类动态域均依据壁面边界建立。随着扰动向周围流动传播,包围着翼型的这2 类动态计算域也逐渐扩大。采用多重网格方法后,对流动态域随壁面扰动迅速向远处扩张。在第5 步时,对流动态域已经包含54.5%的预设计算域单元。由4%Nmax的情况可知,对流动态域会增长到整个预设计算域,而最大黏性动态域只停留在近壁区。由于流场解的变化,当对流动态域保持在最大范围时,黏性动态域会先开始缓慢缩小。当流场求解开始收敛时,对流动态域会从最上游远场区域开始逐渐向壁面收缩,如33%Nmax的情况所示,并带动黏性动态域一起缩小,如57%Nmax的情况所示。求解结束时,2 类动态计算域消失,流场达到定常态,上壁面的激波被很好地捕捉,如100%Nmax的情况所示。
图8 的下半子图对比了不同网格层上对流、粘性动态域的区别。由于网格的差异,2 类动态域的范围都会随着网格的粗化而有所变大。由57%Nmax的情况可知,由于上翼面激波附近的流动变化剧烈,求解较难收敛,因此,上翼面动态域的缩小被激波所阻挡,而下翼面的动态域缩小明显快于上翼面。
表5 和图9 将本文采用3 层粗网格的数值结果与实验数据进行了对比,表5 中CN表示法向力系数,ΔCN/CN表示法向力系数偏差。本文所计算的传统多重网格方法和多重网格-扰动域推进方法所得的气动力均能与实验结果很好地吻合,气动力偏差低于1.6%。图9 中,传统多重网格方法和多重网格-扰动域推进方法预测的翼型表面压力分布完全重合,两者与实验数据也吻合良好。因此,本文所使用的传统多重网格方法和多重网格-扰动域推进方法能够提供正确的湍流流动数值解。
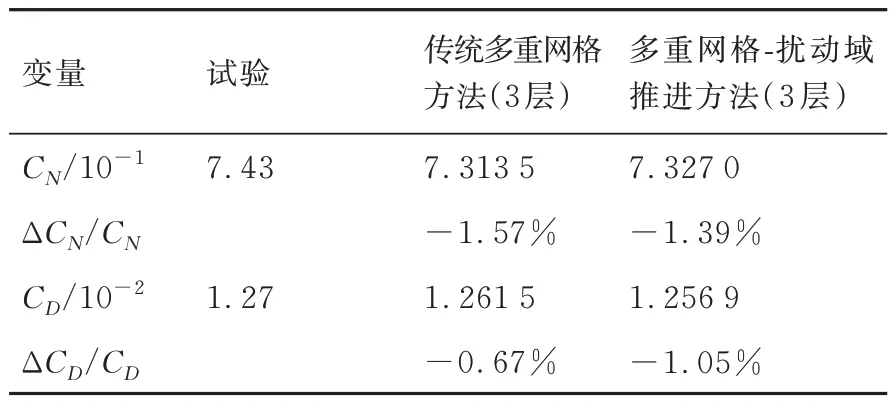
表5 RAE2822 翼型的气动力对比Table 5 Comparison of forces on RAE2822 airfoil
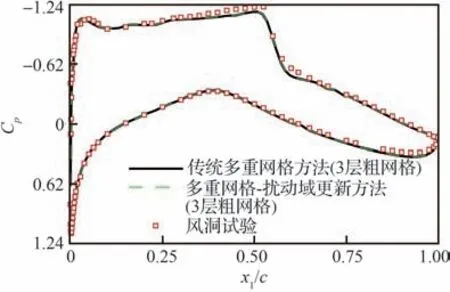
图9 RAE2822 翼型压力系数分布对比Fig.9 Comparison of pressure coefficient distributions on RAE2822 airfoil
图10 对比了RAE2822 翼型算例中多重网格对对流、黏性2 类动态域网格量变化的影响。多重网格方法影响对流动态域的规律与无黏情况一致。对于黏性动态域,多重网格-扰动域推进方法中黏性动态域仍保持每次只新增紧邻的一层单元,因此粗网格层数的不同并未对黏性动态域的增大速率产生影响。不过,粗网格层数为2 层、3 层情况的最大黏性动态域会明显小于未使用多重网格的情况。这一现象主要源自黏性动态域的范围与流动参数密切相关,而多重网格方法可加速流场的收敛;即在相同迭代步时,采用粗网格情况对应的流场解更接近定常解。因此,采用多重网格与否会对最大黏性动态域的范围产生影响。

图10 RAE2822 翼型动态域网格量变化曲线Fig.10 Evolution of number of cells in dynamic compu‐tational domains for RAE2822 airfoil
图11 展示了RAE2822 算例中考虑的所有情况的收敛曲线。所有情况均达到了收敛条件。对于湍流问题,多重网格-扰动域推进方法也同样具有显著的加速效果。加速效果源自3 方面:其一,对流动态域的自适应增大、缩小可同时降低细、粗网格的计算量;其二,黏性动态域可有效甄别黏性效应主导区域,非黏性效应主导区域未计算控制方程黏性项;其三,达到相同收敛条件所需的总迭代步数降低。

图11 RAE2822 翼型收敛曲线Fig.11 Convergence histories of RAE2822 airfoil
表6 展示了本算例中采用不同层粗网格扰动域推进方法的加速效果与求解精度。多重网格-扰动域推进方法在传统多重网格方法加速的基础上还可再提升53.9%~57.9%的计算效率。与无黏NACA0012 情况相同,多重网格-扰动域推进方法的求解精度会随粗网格层数的增加而提升。与无粘NACA0012 情况不同的是,本算例中采用3 层粗网格情况所获得的扰动域推进时间节省量大于采用2 层粗网格或未采用多重网格的情况。由图11 可知,这主要是由于采用3 层粗网格的传统全局更新方法的加速效果不佳而导致的。采用3 层粗网格时,传统全局更新方法的收敛曲线出现了明显的振荡,导致其相比于采用2 层粗网格的情况并未提升效率。

表6 RAE2822 翼型的扰动域推进时间效果Table 6 Acceleration effects stemming of DRUM for RAE2822 airfoil
表7 给出了本算例中多重网格-扰动域推进方法相比于未使用多重网格的传统全局更新方法的时间节省量。对比可知,采用3 层粗网格的多重网格-扰动域推进方法获得了最优的加速效果,可节省90.4%的计算时间。

表7 RAE2822 翼型的总加速效果Table 7 Total acceleration effects of DRUM for RAE2822 airfoil
综上所述,本算例验证了多重网格-扰动域推进方法对亚声速湍流流动模拟的适用性。得益于同时降低细、粗网格的计算量、无黏-黏性流动自适应分区计算和减少总迭代步数,多重网格-扰动域推进方法可在传统多重网格方法的加速效果上,进一步显著提升计算效率。
4 结论
在作者前期提出的扰动域推进方法计算框架中,融入多重网格加速技术,提出了多重网格-扰动域推进方法。着重建立了粗网格上动态计算域的演化逻辑,设计了对结构网格更为普适的新型粗网格生成策略,并对典型算例进行了验证演示,得到以下结论:
1)多重网格-扰动域推进方法通过采用随数值扰动传播而增大、随求解收敛而缩小的动态计算域,对于可压缩流动,尤其是亚声速流动,具有显著的加速效果。典型算例验证结果表明,多重网格-扰动域推进方法可在传统多重网格方法加速的基础上再将计算效率提升57.9%。
2)多重网格-扰动域推进方法的加速原因包括3 方面:其一,对流动态域的自适应增大、缩小可同时降低细、粗网格的计算量;其二,黏性动态域可有效甄别黏性效应主导区域,非黏性效应主导区域无需计算流动控制方程的黏性项;其三,达到相同收敛条件所需的总迭代步数降低。
3)提出的新型粗网格生成策略,可消除结构网格生成粗网格对单元数目的限制,提高了多重网格-扰动域推进方法的适用性。

