多层介质空间电荷测试系统的等效表征模型与信号畸变特性

史昀祯, 程思闳, 任瀚文, 高浩予, 綦天润, 李庆民

(新能源电力系统全国重点实验室(华北电力大学), 北京 102206)

1 引言

随着电力系统运行电压和容量的不断提高,新能源化电力网络属性对输变电装备绝缘设计提出了空前挑战[1],特别是高频电力变压器、气体绝缘开关设备等新型电力系统装备中存在的绝缘问题[2],直接影响电力系统的安全稳定运行。其中,绝缘材料性能劣化与失效的主要原因在于直流高压下的空间电荷积聚极易造成局部电场畸变,尤其在高频电力变压器等存在绝缘复合结构的高压电器装备中,材料界面处电荷积聚问题最严重,是整个绝缘系统的薄弱环节[3-5]。因此,研究多层电介质空间电荷分布与积聚机理具有重要的意义。

电声脉冲法(Pulsed Electro-Acoustic,PEA)由于结构设计简单、硬件要求较低、电气安全性较高等特点,相对于其他测量方法得到了更广泛的应用[6,7]。针对电声脉冲法下单层介质空间电荷测量结果的仿真分析与评估方法已较为完善[8],但针对多层介质测量情况,仍有许多问题需要解决。相较于单层介质情况,多层介质测量同时受多界面声波产生及反射、介电常数不连续、厚度不相同等多重因素影响,分析过程更为复杂。此外,在开展仿真模拟时,以往研究均假设半导电电极部分与被测试样、压电传感及背衬吸声部分的声阻抗基本相等,以消除声波反射对实验结果的影响[9-11],但实际测量过程中采用的电极与试样等材料的声阻抗并不能完全匹配[12,13]。传统基于双极性载流子模型的空间电荷仿真方法,只能模拟电荷积聚的动态过程[14,15],无法分析反射声波、材料参数等对测量系统本身的影响。因此,有学者使用Comsol有限元仿真手段,对多层介质声波界面反射开展了初步研究[16],但并未考虑声波传播衰减、多层介质厚度变化与声阻抗匹配程度对测量结果的影响,导致其模拟结果与实际测量结果存在较大差异。因此,亟需建立适用于多层介质下的电声脉冲法测量仿真模型,分析声阻抗匹配程度等对测量结果的影响,以支撑多层介质测量结果分析与实际系统的性能评估。

围绕上述问题,本文分析研究了PEA测试时的信号传递和基本传输线系统中信号传播的相似性,据此提出了PEA系统的等效表征原理。进一步利用实测与仿真结果比较,验证了传输线模型的可靠性。基于所构建模型,针对双层介质的不同厚度、多层介质的不同层数以及声阻抗的匹配程度开展了仿真模拟,研究结果可为多层介质空间电荷测量结果准确分析提供理论基础。

2 电声脉冲法声波传播的等效传输线型

电声脉冲法测量空间电荷时,电脉冲会扰动试样中的空间电荷,使其产生声波,包含电荷信息的声波传播到压电传感器的过程中,会经过不同材料的衰减以及不同介质之间的透射反射,传播过程较为复杂。因此,构建声波传播过程的等效传输线模型是研究多层介质电荷分布机理的必要基础。

2.1 声波传播与传输线电压波传播的等效原理

本文拟使用电压和电流、声波压强和声速的等价关系,以对波在电传输线和声学介质的传播过程进行等效化处理。在传输线中,两个导体之间电位差和电流的相互作用可表示为[17]:

(1)

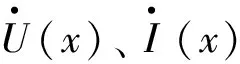
(2)

式中,衰减常数α为电压或电流经单位长度的传输线后振幅减小的常数;相位常数β为单位长度上电压或电流相位的变化量;传输线的单位电阻、电导、电感和电容则由R、G、L、C来表征。

声波在介质中传播的方程满足如下关系[18]:

(3)

式中,p(x,t)为声波压强;v(x,t)为介质中声波的传播速度;kc为由衰减常数αc和波数组成的复数,与式(1)中的传播常数γ类似。

结合式(1)与式(3),PEA系统与传输线模型中的信号传播表征公式相似,即说明信号传播过程相同,由此可进一步推导得到式(4)给出的两个模型中关键参量等效关系[19]。由式(4)可知,PEA系统中的声波传播过程与特性,可以等效为传输线中的电压电流传输。

(4)

式中,ρ为材料密度;A为声波传播横截面积;αv和αtc分别为由粘性损耗和热传导引起的衰减系数。

2.2 PEA中声波传播过程的等效传输线模型

图1给出了PEA的基本系统组成。测量过程中,外施高压引发试样电极界面和内部电荷振动发出声波,进一步朝传感部分和上电极侧传输,同时发生界面透射和反射行为,其基本关系如式(5)所示[20]。

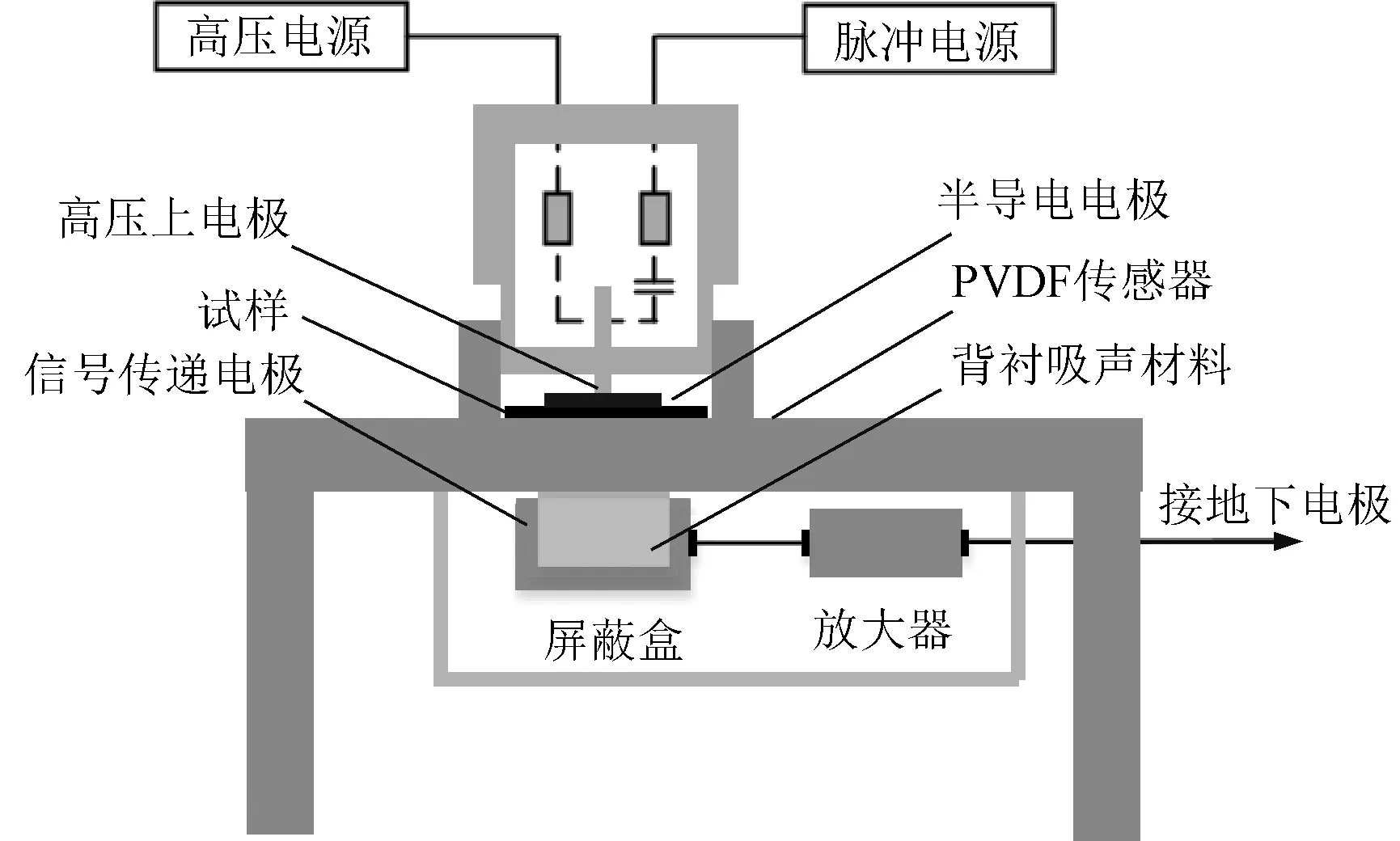
图1 PEA法的系统结构Fig.1 System structure of PEA method

(5)

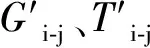
根据声波与电压电流波等效关系,对声波传播过程进行等效化处理。在此之前,需进行一定的假设:①电荷振动产生的声波与激励波形相似;②积聚电荷产生的声波仅沿试样厚度方向传输;③不同声波的相遇叠加具有线性[21]。基于前文等效关系与上述假设,构建声波传播全过程传输线模型,如图2所示。其中,核心模块Z4为压电传感器声阻抗,其等效原理如图3所示,由压电传感器获得的测量结果,即为PEA测试结果[22]。同时,鉴于实际测量过程中试样界面会积聚大量感应电荷,分别在试样两端设置双指数电源进行等效。这里采用的双指数电源为串联形式,主要是因为:根据声波产生与传播原理,在两介质之间的界面处,声波产生后会向两侧介质中传播,且在不同介质中传播声波的大小与介质的声阻抗成正比,采用双指数电压源串联形式,电压波也会分别向两侧传播,且不同介质中电压波的大小与介质的特征阻抗成正比,因此电压源串联后,电压波的传播与不同界面处声波的传播具有相似性,可以进行等效。而电压源采用并联形式,虽然电压波也会向两个方向传播,但是不会经过与电压源并联的材料,这与电声脉冲法测量系统中声波的传播过程不相符。此外,在模型首末两侧设置与相邻模块相等声阻抗的集中参数元件Z6和Z0,以保证声波在两侧不会出现反射问题,方便后续研究讨论。

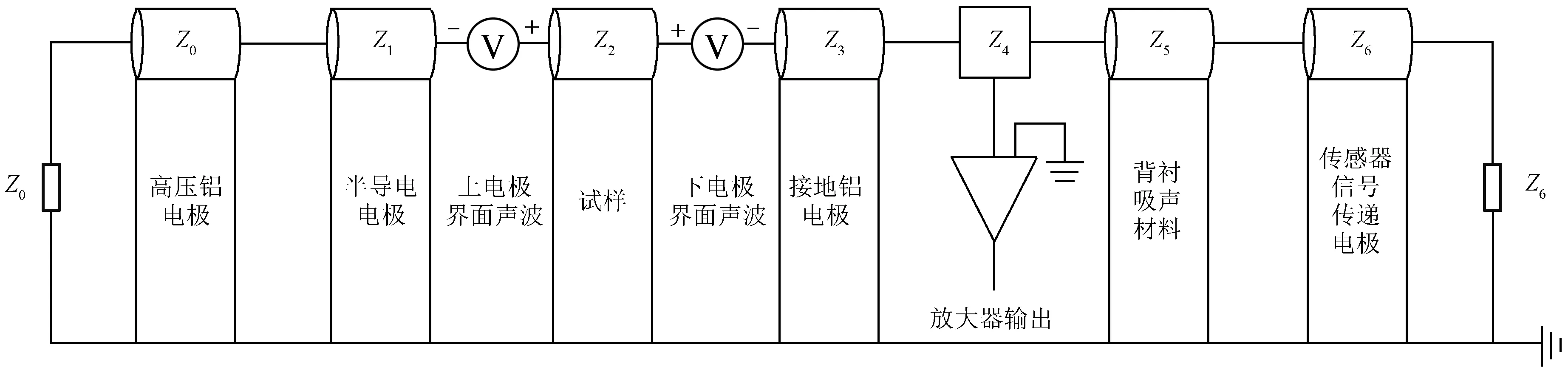
图2 PEA中声波传播的等效表征Fig.2 Equivalent characterization of acoustic propagation inside the PEA system

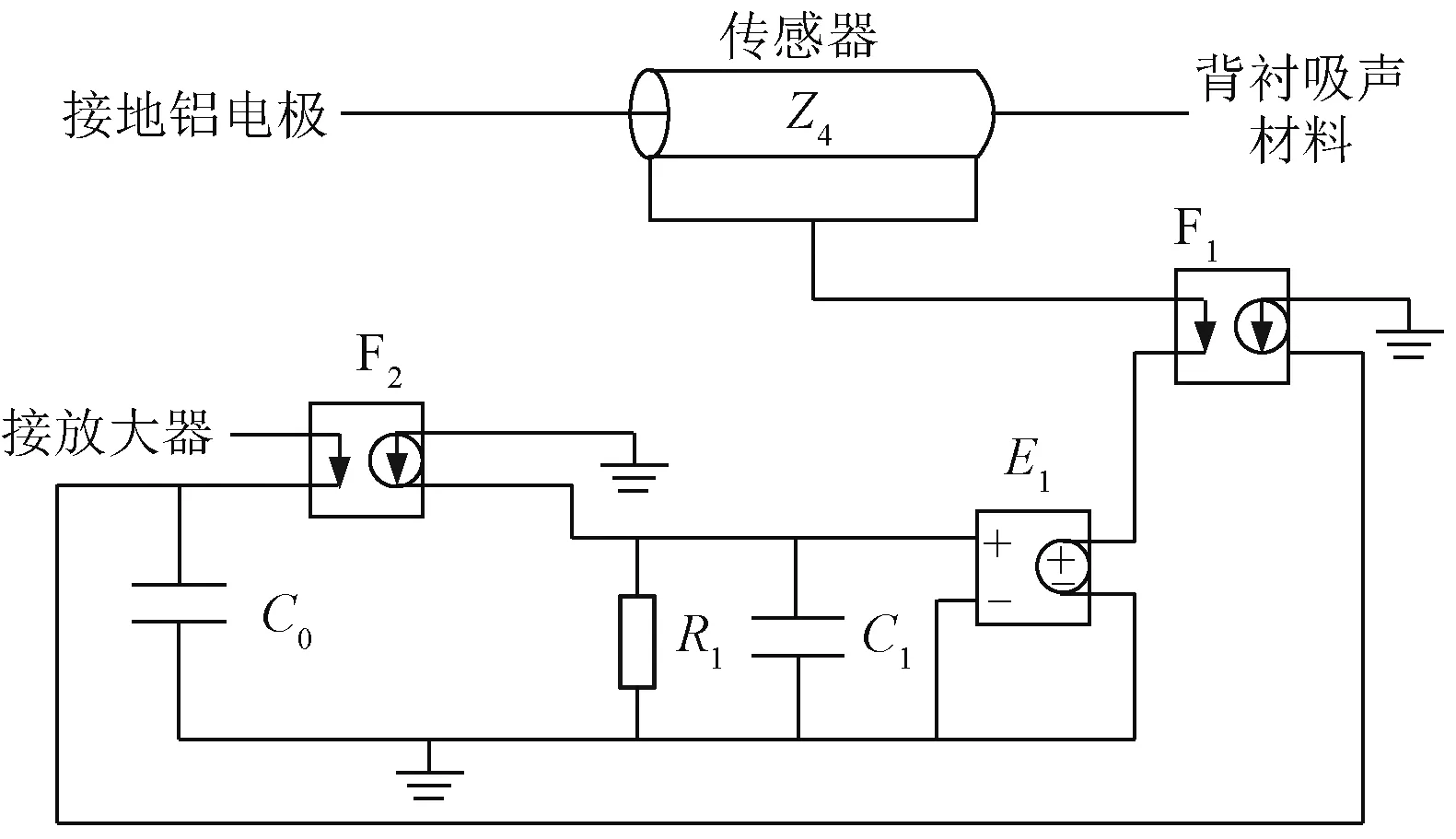
图3 传感部分的等效表征Fig.3 Equivalent characterization of transducer part

针对图2所示的等效模型,材料密度、声速和衰减系数等参数设置见表1,衰减系数的设定主要来源于文献[23]中的材料参数与文献[19]的衰减系数计算方法,可以较为准确地反映声波传播的衰减过程。其中,PVDF指聚偏氟乙烯(Polyvinylidene Fluoride),为压电传感器材料。

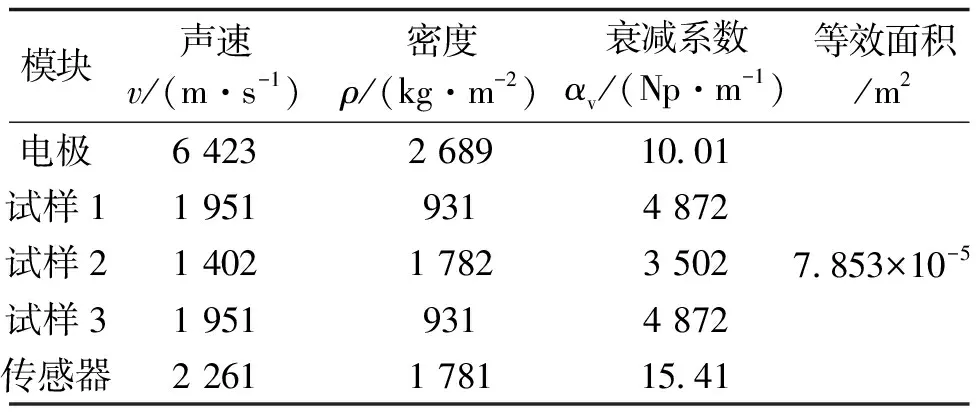
表1 各个模块的声学参数Tab.1 Acoustic values of different parts

鉴于PEA中所采用铝电极直径通常为10 mm,结合表1中材料基本参数,计算获得传输线模型各元器件电阻、电感和电容参数见表2。由于仿真过程中对热传导所引起的衰减进行了忽略,因此,设定不同材料的电导为零。此外,认为试样和半导电电极、传感和吸声部分声阻抗分别相等,以方便后续研究分析。需说明,单层介质模拟使用试样为试样1,多层介质仿真中所使用试样将在各节中另做说明。

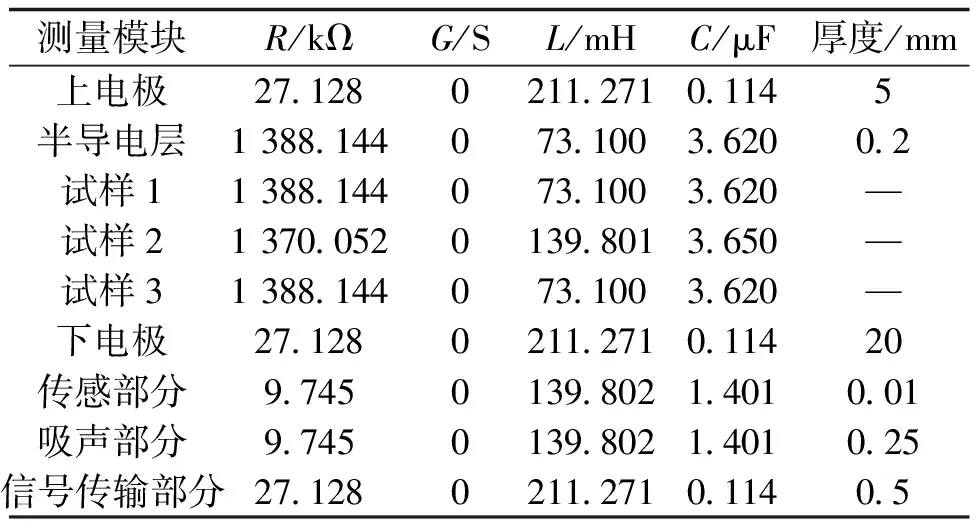
表2 等效表征模型的基本参数Tab.2 Basic parameters of equivalent model

3 等效传输线模型的实验验证与声波传输特性分析

3.1 等效模型的可靠性验证

本文拟通过实验与仿真结果比对,对等效模型可靠性进行验证。PEA系统中,脉冲源输出激励脉宽为5 ns、最大输出幅值为600 V、被测试样厚度为250 μm、压电传感器选用厚度为10 μm的PVDF薄膜,仿真模拟参数设置与实验测试所用电极和试样的基本参数均保持一致,具体见表1。仿真模拟与实验测试的电声脉冲波形结果如图4所示。

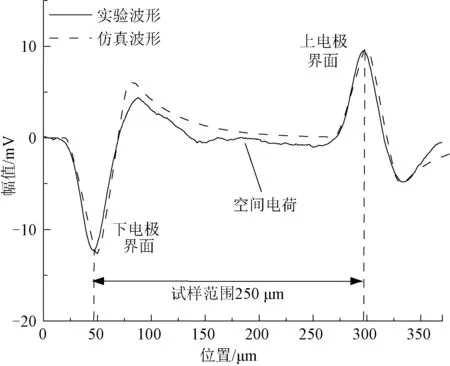
图4 仿真模拟与实验测试波形对比Fig.4 Comparison of simulation and experimental results

由图4可得,实验与仿真获得的上下电极界面处产生的电压脉冲具有较高的一致性,同时,试样内部电压波形变化也呈现相同趋势。因此可得,所构建等效传输线模型具备一定的等效性,可用来模拟声波在PEA测试系统中的传播过程。其中,试样范围内电压波形的微小差异主要源于实际测试过程中试样内部积聚了少量空间电荷,而仿真中设定试样内部无空间电荷积聚。下文在使用该模型分析多层介质时,会进一步结合声波的传播过程对模型可靠性进行验证。

3.2 多层介质中材料厚度对测量结果的影响

双层介质试样中,由于两个介质材料的声阻抗不同,因而声波传播经过界面处时会发生透射和反射现象,以下针对双层介质中声波的传播过程进行详细的分析和讨论。

假定双层介质试样分别选择表2所示的试样1与试样2,厚度分别设置0.2 mm、0.1 mm,结合表1中各个模块的基本声学参量进行计算,可以得到图5所示的双层试样声波传播时间及过程。

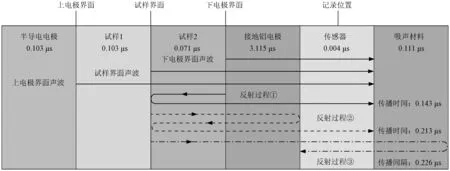
图5 声波传播的过程分析Fig.5 Process analysis of acoustic wave propagation

声波通过每个模块需要的时间已在图5中标明,同时标注了信号①～③的传播时间,分别代表PEA下电极信号传至传感器时与该信号到达传感器时的时间差。进一步,考虑到声波传播过程中的衰减与反射,本文将重点针对以下三个反射过程开展分析:反射过程①:下电极界面产生的声波在试样1-试样2界面处发生反射;反射过程②:试样界面产生的声波先后在下电极界面和试样1-试样2界面处发生两次反射;反射过程③:下电极界面产生的声波,在吸声材料与传感器不相邻的界面处发生反射。如图5所示,三个主要反射过程所对应传播时间分别为0.143 μs、0.213 μs和0.226 μs。

进一步,基于所构建等效传输线模型对双层介质声波传播过程开展模拟,考虑到两种试样材料不同,其界面处由于介电特性差异同样会产生声波信号。为分析该界面声波的影响,在两个试样间设置了一个双指数电压源。由此,双层试样下PEA测量信号模拟结果如图6所示。

图6 双层试样的仿真波形Fig.6 Simulation waveforms of double-layer samples

根据上述结果,除试样各个界面的电荷峰以外,在有效波形附近还存在三个波峰,图6中给出了三者与上电极界面信号之间的间隔时间,这与理论分析中,双层介质声波传播过程所涉及的三个主要反射过程完全对应。由此,进一步验证了本文所构建等效传输线模型在多层介质情况下的仿真可靠性。

由于电声脉冲法实际测量过程中,着重关注信号范围为上下电极界面信号之间部分。由仿真结果可以发现,反射过程①所产生信号处于有效信号范围区间内,为消除该信号对电荷测量的影响,应使该信号传播时间大于上电极界面声波传播至传感器的时间,即满足声波在试样2传播的时间大于在试样1中传播的时间,由此,双层介质中试样厚度应满足式(6)所示要求:

(6)

式中,Len1、Len2分别为试样1和试样2的厚度;v1、v2分别为两个试样中的声速。

基于式(6)分析,设置试样2厚度为0.2 mm,以消除反射过程①对测量结果影响,模拟获得PEA测量信号如图7所示。

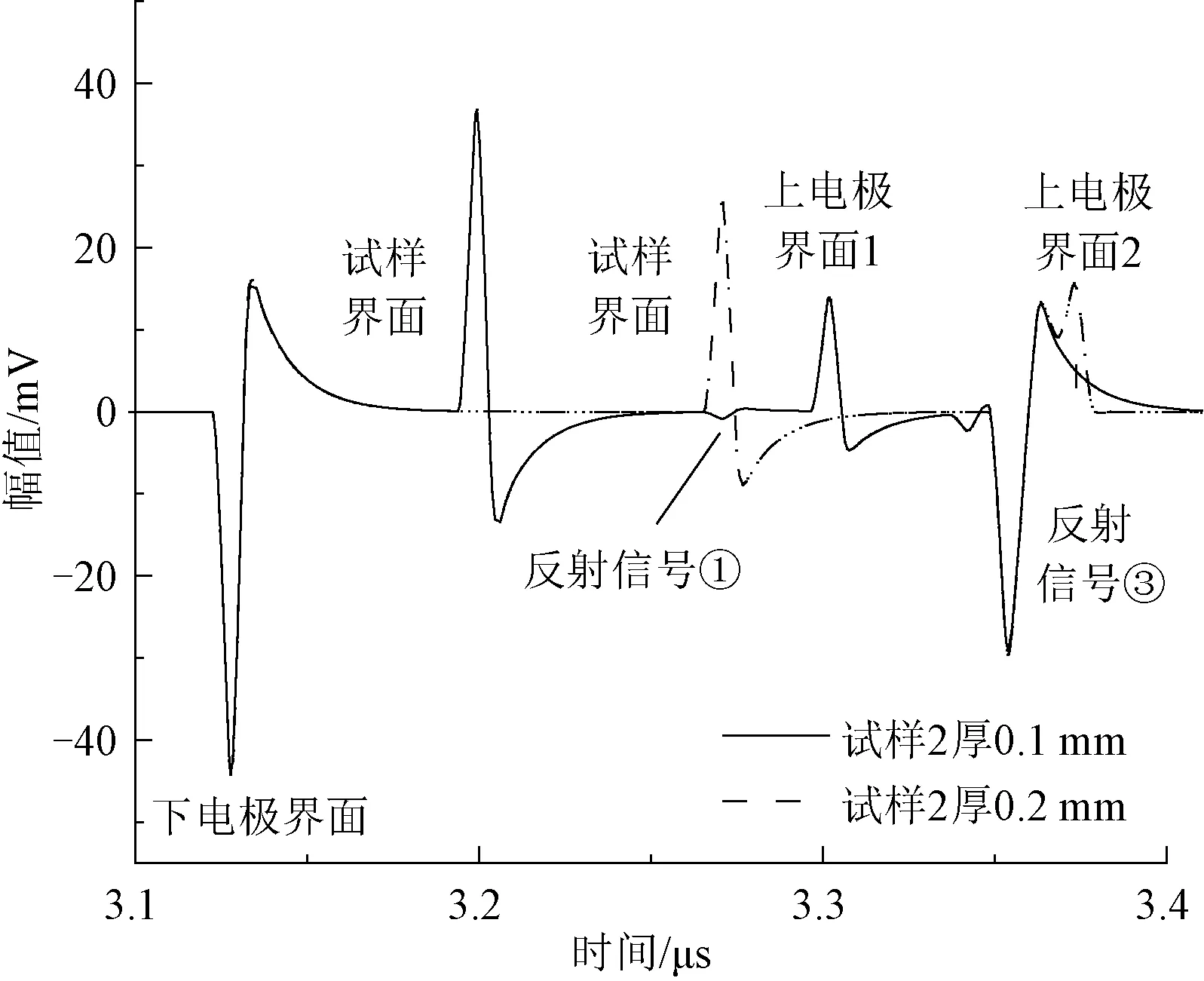
图7 不同试样厚度的仿真结果Fig.7 Simulation for different thicknesses of sample

由图7可以发现,更改试样厚度后,反射信号①不在影响有效信号范围内,但是由于试样厚度增加使得有效信号的时间范围增加,信号③同样出现在有效信号范围内,并叠加在了上电极侧的界面信号上,因此,为防止反射信号③的干扰,提高测量准确度,吸声材料不仅要满足良好的吸声特性,厚度也应满足如下关系:

(7)

式中,Lenx、vx分别为吸声材料的厚度和声速。进一步,基于式(7)分析,调整吸声材料厚度为0.5 mm,以消除反射过程③对测量结果影响,模拟获得PEA测量信号如图8所示。

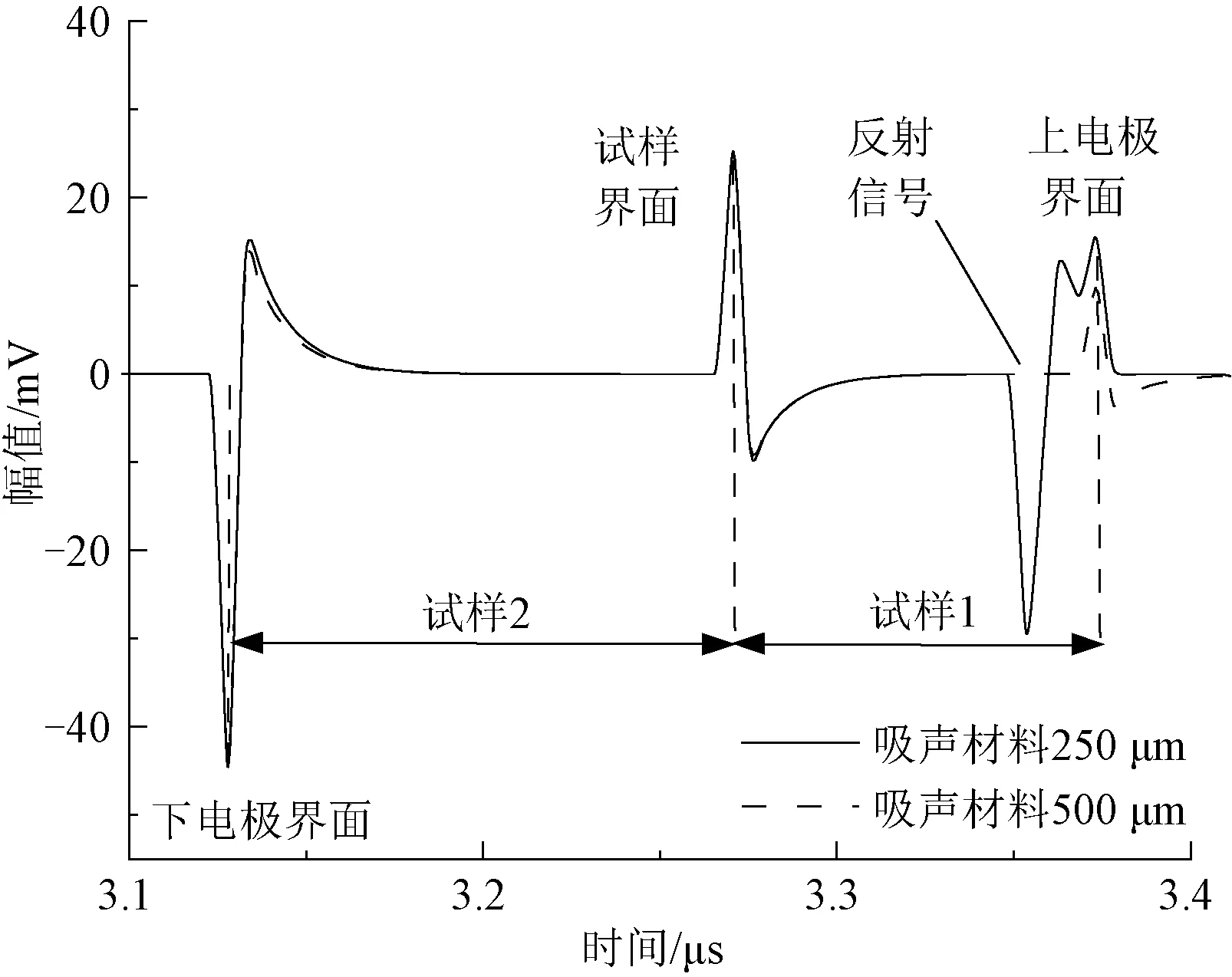
图8 吸声材料不同厚度的仿真结果Fig.8 Simulation results for different thicknesses of sound-absorbing materials

由图8可以发现,改变吸声材料的厚度,有效信号范围内不再存在反射信号的干扰。综上所述,双层试样和背衬吸声部分厚度需满足式(8)基本关系,以消除声波反射问题对有效测量信号的影响。

(8)

3.3 多层介质中层数对测量结果的影响

结合双层介质的仿真过程,本文以三层介质为例,分析多层介质中层数对测量结果的影响。假定三种介质分别为表2中的试样1、试样2和试样3,厚度依次为0.1 mm、0.1 mm和0.2 mm,其他元器件参数均保持不变,声波在介质中传播过程如图9所示。

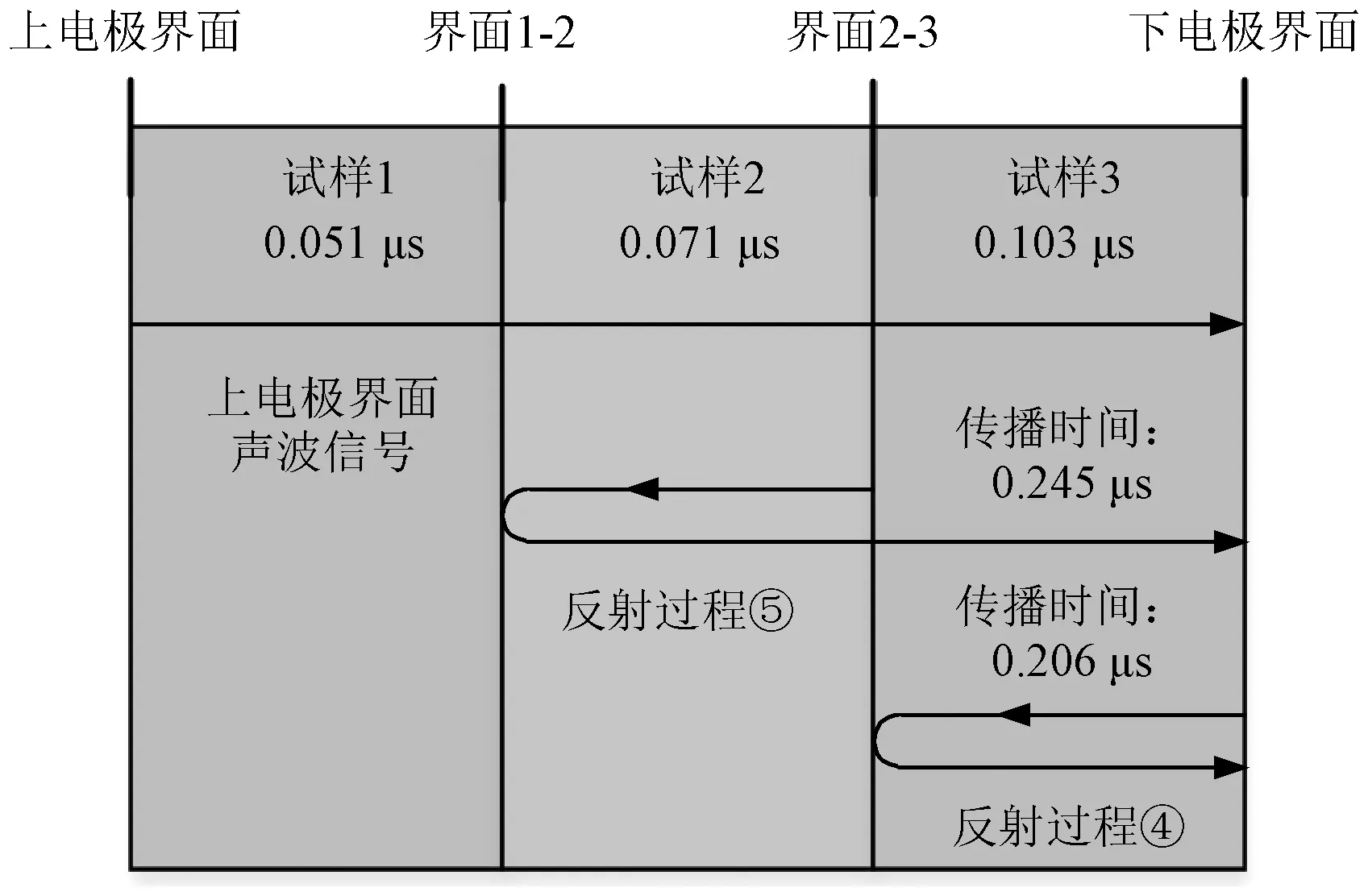
图9 三层试样的声波传播过程Fig.9 Acoustic propagation process of triple-layer samples

如图9所示,与双层介质情况类似,三层介质中需重点关注反射过程④和反射过程⑤。反射过程④:下电极界面产生的声波在试样2-试样3界面处发生反射。反射过程⑤:下电极界面产生的声波在试样1-试样2界面处发生反射。可以发现无论三层介质厚度和声速如何设置,信号④或信号⑤始终都是所有反射声波中时间最短的,是最有可能干扰到有效信息测量的反射杂波信号,因此只需要同时保证信号④和信号⑤在有效时间段范围之外,即可保证测量信号不受反射信号干扰。结合材料声速和厚度进行计算,其传播时间分别为0.206 μs和0.245 μs。鉴于上电极界面声波信号传播时间为0.225 μs,反射过程④和⑤所产生声波信号将依次在上电极界面声波信号两侧分布。三层试样下PEA测量信号模拟结果如图10所示。

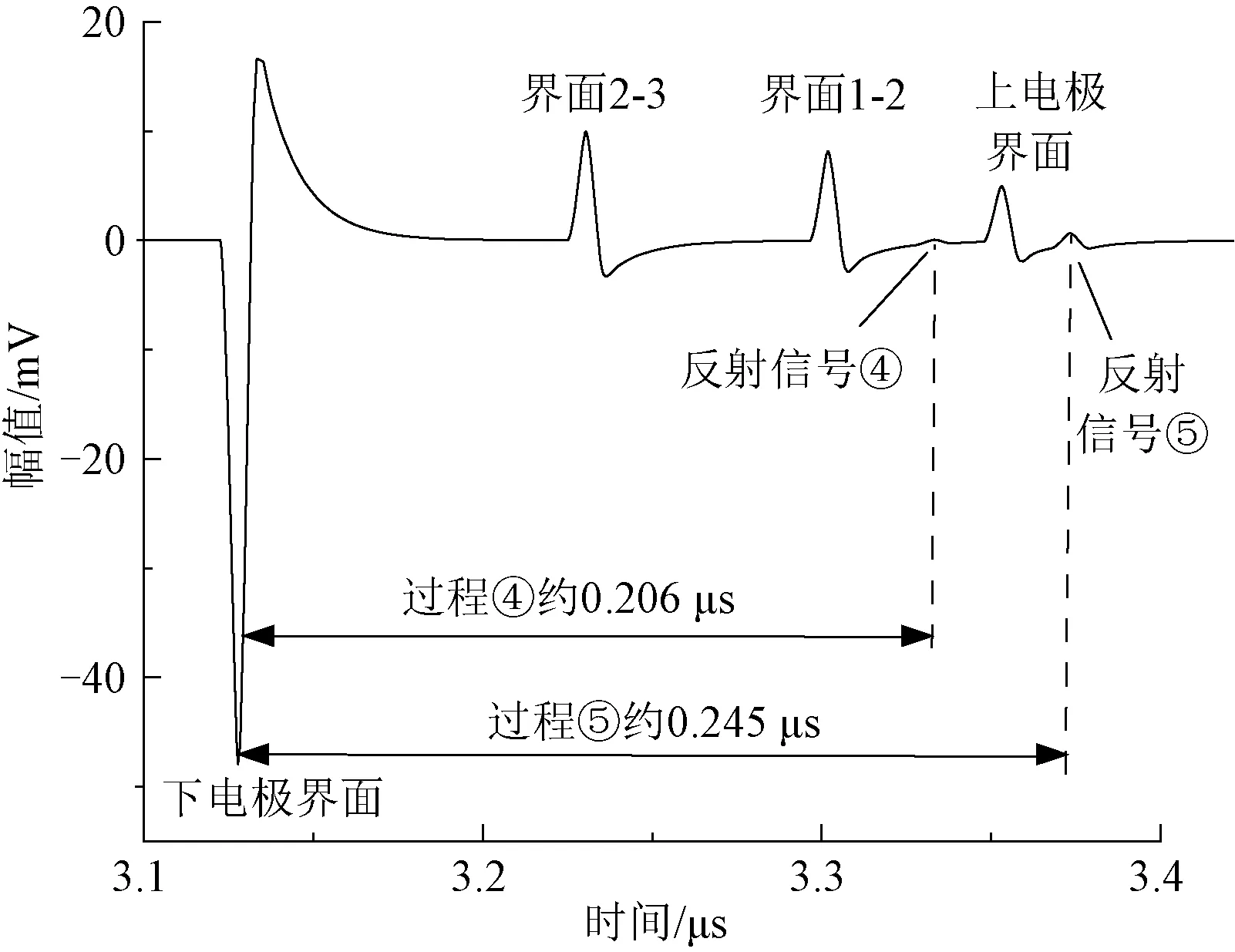
图10 三层试样的模拟波形Fig.10 Simulation waveforms of triple-layer samples

如图10仿真结果所示,模拟结果中除包含试样界面和上下电极界面处电荷电压峰外,还出现了2个新的波峰,分布于上电极界面声波信号左右两侧,且在时间尺度上与反射过程④和反射过程⑤相对应,这与上文理论分析结果相对应。同时,由于反射过程④所产生信号处于有效信号范围区间内,会对电荷测量结果产生干扰,因此,为消除反射信号对有效信号的影响,结合2.1节双层介质中相关推论,得出PEA测量三层介质时应满足如下要求:

(9)

由此,得出以下推论,当多层介质中层数为k时,为消除反射信号的影响,应满足要求如式(10)所示。

(10)

式(10)中,第一个公式的物理意义为:第k个试样界面产生声波经一次反射传播到传感器的时间大于上电极界面声波信号传播到传感器的时间,即第k个试样界面产生的声波反射信号在有效信号范围之外;第二个公式物理意义为:第一个到达传感器的声波信号在吸声材料内来回反射的时间大于上电极界面声波信号直接传播到传感器的时间,即经吸收材料反射的声波信号在有效信号范围外。综上,当试样和吸声材料的厚度满足式(10)时,可有效减少声波反射对测量结果的影响。

3.4 材料声阻抗匹配特性的影响分析

应用PEA测试时,以往研究均认为半导电电极部分与被测试样、压电传感及背衬吸声部分的声阻抗完全相等,以消除声波反射对测量结果的影响,但实际测量过程中无法做到完全匹配。因此,本文拟将所构建模型中半导电电极(Z1)和背衬吸声材料(Z5)的声阻抗调整为原来的1.5倍,不改变试样1(Z2)和传感器(Z4)的声阻抗,以此来研究声阻抗不完全匹配对双层介质下电荷测量结果的影响,仿真结果如图11所示。

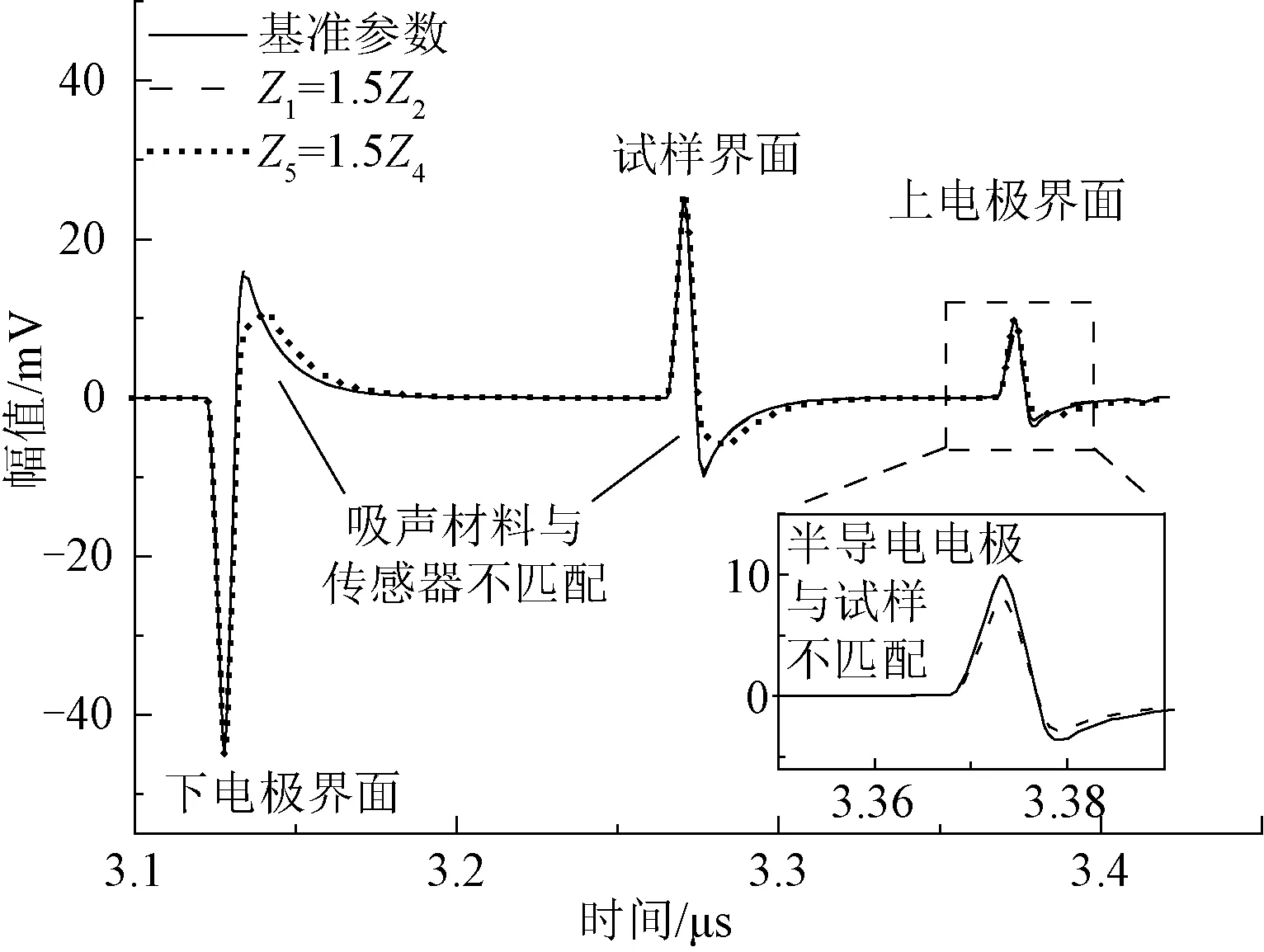
图11 两种声阻抗不匹配条件下的模拟波形Fig.11 Simulation waveforms under the two conditions with mismatched acoustic impedances

根据图11中的模拟波形,当半导电电极与相邻试样声阻抗不匹配时,上电极界面处的声波幅值较阻抗匹配时稍有降低,试样界面和下电极界面处的声波幅值则不受影响。根据式(5)中的声波产生系数计算公式可知,对于界面声波向试样方向传播的分量来说,半导电电极声阻抗与其产生系数呈负相关关系,因此,当其他参数不变,仅增大半导电电极声阻抗时,产生系数减小,向试样方向传播的分量幅值变小,因而出现图11所示的上电极界面处的声波幅值降低的情况。

同时,对比吸声材料声阻抗改变前后波形可发现,当传感器与吸声材料声阻抗不匹配时,三个界面处的声波幅值虽然没有变化,但其波形均发生了一定程度的展宽。究其原因,是因为在传输线模型中,压电传感器测量主要基于前后界面电压差,当传感器与吸声部分的声阻抗存在差异时,声波在两者界面处存在反射情况,使得声波在传感器中传播时间变长,进而影响了传感器界面处电压幅值,最终表现为波形的展宽。

4 结论

(1)通过分析声波传播与电压波传输的等效性,研究建立了针对PEA测量系统的声波等效传输线模型,并通过与实验测量波形的比较,对模型可靠性进行了验证。

(2)基于所构建传输线模型,开展了多层介质下的电荷测量仿真模拟,阐明了试样及吸声层厚度对测量结果的影响,并基于此,进一步提出了适用于多层介质的电声脉冲测量遴选标准,即声波在任意一层试样中的传播时间需大于声波在该层试样之前所有试样中的传播时间之和,同时声波在吸声材料内部往返传播时间应大于其在所有试样中的传播时间总和。满足以上条件可有效减少声波反射对测量结果影响。

(3)通过调整电极、试样等关键环节声阻抗参量,针对声阻抗匹配程度对电声脉冲测量结果的影响作用开展了仿真模拟。研究指出,若试样与其相邻半导电电极的声阻抗不相等,将影响界面处的声波产生系数,进而改变上电极界面侧的被测信号幅值;若传感器与吸声部分的声阻抗不相等,会导致所测结果中所有界面处电压波形发生畸变,出现波形展宽和拖尾等情况。