丹江水文站水文要素监测方案分析
魏徐涛
(贵州省水利科学研究院,贵州 贵阳 550002)
本文以丹江水文站为背景,对该水文站精测流量测验进行常测法精简分析,其研究意义为,总结了该地区水文站采用流速仪测流和ADCP 测流,水文监测采用站队结合以及水文巡测。该地区水文站属于国家一类精度水文站,通过对水文站进行频率分析,得出高水位、低水位以及中水位。根据摘录的系列资料确定该年水位处于中水水位,制定中水水位的常测法精简分析。常测法精简分析通过对测速垂线位置以及相对误差绝对值二者共同分析对比得出。方案三保留12 条测速垂线精简方案符合丹江水文站中水水位精简分析,能够代替其精测法流量测验。
1 国内研究进展
我国的水文监测手段已由传统人工观测逐步转向自动化监测,雷达测雨、无人机、遥感遥测等新技术广泛应用,水位、雨量监测已全面实现自动测报,流量监测中,先进的声光电新技术新设备正大力推广。我国在不断提高水文监测能力,建设水文监测系统,从探索阶段到发展阶段再到提高阶段三步走。利用学习并且引进国外设备,研究先进的水文监测方法和技术,引进美国的设备,并且加以创新进行国产化,通过和国外先进的水文监测设备比较,清楚意识到我国的水文监测技术在精确度、稳定性以及工程技术仍然落后国外的先进技术和测验能力。
2 降水观测
水文循环一共有四个过程,分别是蒸发、降水、下渗以及径流。对于收集水文站的数据,降水这一要素成为了丹江水文站必须观测的水文要素。降水是云进行降落,除此之外也包括从大气沉降到地面的液态或者固态的水汽凝结物。降水的形式多样,主要分为雨、雹、露、雾凇、白霜和雾降水。常用的雨量观测设备有三种。水文测站最常用的是雨量器、虹吸式雨量计、翻斗式雨量计。
丹江水文站降水观测设备采用的是翻斗式雨量计和称重式雨量计,设有雨量观测场和室内翻斗式雨量计,水文站的观测人员在每日8 时和20 时分别量取前12 小时的降雨量。摘录丹江水文站1951年~2014年降雨量平均值,绘制平均降雨量过程线,见图1。
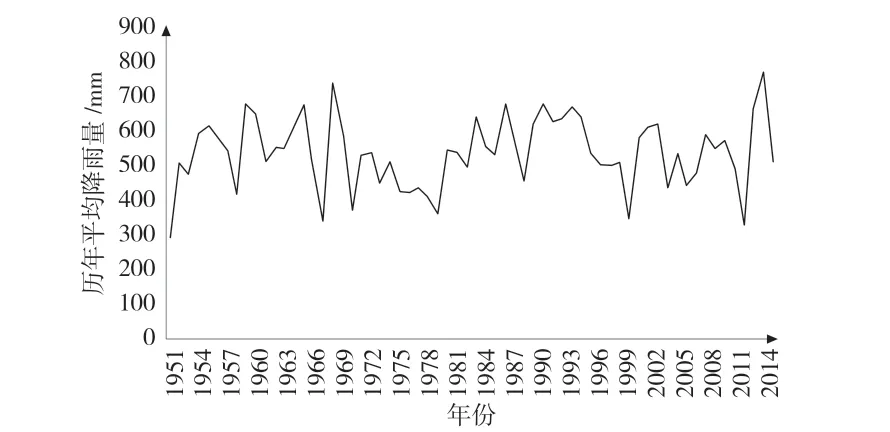
图1 丹江水文站历年平均降雨量过程线
从摘录的丹江水文站年降水量特征值以及绘制的丹江水文站历年平均降雨量过程线图中可知,平均降雨量由高到低排在前五年的分别为 2013年、1968年、1990年、1986年、1959年。
3 水位级划分
3.1 水位级划分原理
针对水位级划分,根据《河流流量测验规范》(GB 501 79-2015)中相关要求,指出首先要计算出对应频率,绘制相应的频率曲线,且水文站按精度分为一类精度和二类、三类精度。
3.2 丹江水文站频率分析
丹江水文站属于国家一类精度水文站,根据水位级划分原理,采用年特征值法进行水位级划分[1]。按照规范要求,最低摘录20年的年份,因此摘录丹江水文站1950年~2014年共65年最高水位、平均水位以及最低水位的系列资料,完全大于20年且符合规范,根据 P-Ⅲ型曲线,运用程序分别计算频率并绘制三个频率曲线。以下频率曲线分别为丹江水文站最高水位频率曲线、平均水位频率曲线和最低水位频率曲线。
(1)最高水位频率曲线见图2,其中,适线参数见表1。

表1 适线参数表
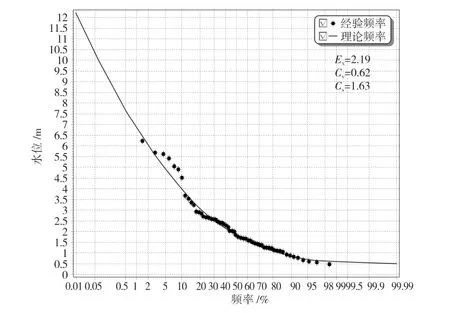
图2 丹江水文站最高水位频率曲线
(2)丹江水文站最低水位频率曲线见图3,其中,适线参数见表2。

表2 适线参数表

图3 丹江水文站最低水位频率曲线
以上为丹江水文站频率分析,根据水位级划分原理对其进行水位级划分。
3.3 丹江水文站水位级划分分析
丹江水文站采用国家一类精度水文站的水位级划分进行划分分析,摘录1950年~2014年共65年的系列资料,运用畅流期水位进行水位级划分。由上述二个频率曲线图,进行反向查询,得出丹江水文站水位级划分如下:
(1)当P=90%时,对应高水位=228.3 m;
(2)当P=50%时,对应中水位=224.8 m;
(3)当P=10%时,对应低水位=224.3 m。根据上述计算结果,绘制丹江水文站水位级划分表格,见表3。

表3 丹江水文站水位级划分
4 测流方案编制
4.1 测流方案
丹江水文站在运用精测法进行流量测验的过程中,采用0.2 和0.8 两点法计算垂线平均流速,从而计算一系列精测值。摘录的数据为2018年4 月~12 月共25 组流量数据,且水位全部位于中水水位,所以对摘录的流量数据做中水测验方案,对16 条测速垂线做精简分析,分别从精简前后流量、精简前后面积以及精简前后垂线平均流速做分析,共整理三个精简分析方案,按照常测法最少测速垂线数目的要求,丹江河水面宽介于100 m~300 m 之间,对应精简后测速垂线数目范围为7~13 条,则方案一为选定精简至8 条垂线,方案二为选定精简至10 条垂线,方案三为选定精简至12 条垂线。
4.2 合理性检查
4.2.1 测速垂线位置图精简分析
根据常测法精简分析的相关要求,绘制三个方案精简前的测速垂线位置和精简后测速 垂线位置曲线,通过对比,选择最佳方案。精简前测速垂线位置图见图4。
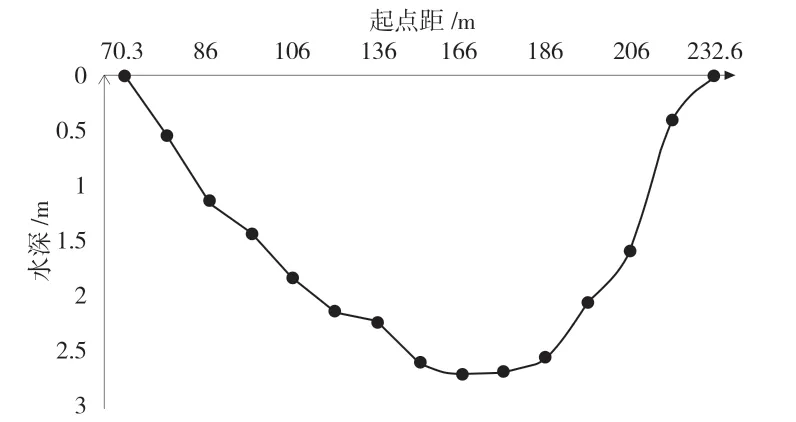
图4 精简前测速垂线位置图
方案一精简至8 条测速垂线位置分别为起点距 (76 m 、86 m 、126 m 、136 m 、156 m、166 m、176 m、206 m),其测速垂线位置图见图5。
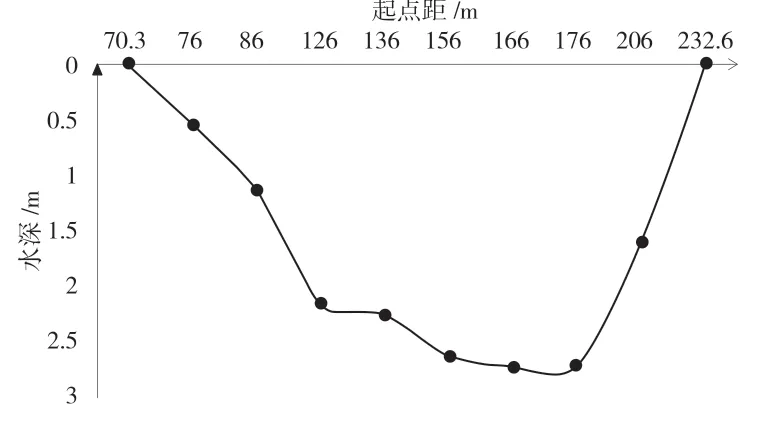
图5 方案一精简后测速垂线位置图
方案二精简至10 条垂线位置分别为起点距(86 m、96 m、126 m、136 m、146 m、166 m、176 m、186 m、196 m、206 m),其测速垂线位置图见图6。
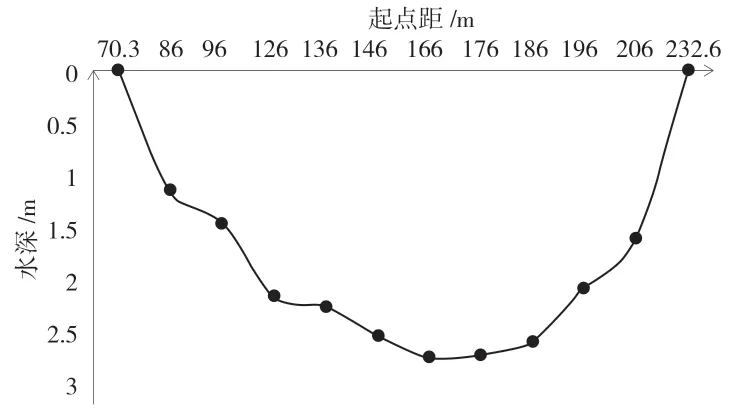
图6 方案二精简后测速垂线位置图
方案三精简至12 条测速垂线位置分别为起点距(86 m、96 m、106 m、126 m、136 m、156 m、166 m、176 m、186 m、196 m、206 m、232.6 m),其测速位置垂线图见图7。

图7 方案三精简后测速垂线位置图
从三个方案精简后测速垂线位置图可得出,方案一测速垂线位置为 76 m 和126 m 之间的分布形态与精测时同一位置分布形态相差过大,方案二测速垂线位置为126 m 和146 m 之间的分布形态与精测时同一位置分布形态相差过大,而方案三精简的测速垂线位 置保留了精测时的所有大致分布形态,与精测时测速垂线位置无太大偏差,因此从测速垂线位置分布图的角度可以得出,方案三为最佳精简分析方案,方案一和方案二舍弃。
4.2.2 精简误差相关分析
(1)精简后流量误差分析
根据常测法精简分析的要求,对精简前流量和精简后流量进行误差计算,累积频率为75%时,误差不得超过±3%;累积频率为95%时,误差不得超过±5%,且要满足系统误差不能超过±1%。根据上述计算成果表,方案一、方案二、方案三精简后流量相对误差绝对值,找到累积频率为75%和95%所对应的相对误差绝对值[2]。经过对比可以发现,方案一在保留8 条测速垂线进行流量精简分析时,累积频率75%时所对应的相对误差绝对值介于10.46%~10.63%之间,已超出±3%范围内;方案二在保留10 条测速垂线进行流 量精简分析时,累积频率为75%时所对应的相对误差绝对值介于2.69%~2.91%之间,累积频率为95%时其相对误差绝对值为符合误差范围要求,即该方案可取;方案三在保留12 条垂线进行流量精简分析时,累积频率为75%时所对应的数值介于1.38%~1.45%之间,同样符合误差范围内,相对于方案二和方案三,从精简后流量分析误差角度,方案三更加可取。
(2)精简后面积误差分析
根据计算成果,在成果中可以查出,方案一对保留8 条测速垂线进行精简分析,当累积频率为75%时多对应的相对误差绝对值介于5.5%~5.66%之间[3],超出误差范围,则不合理;方案二对保留10 条测速垂线进行精简分析,当累积频率为75%时,对应相对误差绝对值介于2.8%~2.81%之间,符合误差范围,当累积频率为95%时,其相对误差绝对值为4.9%,同样符合误差范围;方案三对于保留12 条测速垂线进行精简分析,当累积频率为75%时,对应相对误差绝对值介于0.93%~1.12%之间,符合误差范围,当累积频率为95%时,对应相对误差绝对值介于1.41%~2.97%之间[4],完全符合误差范围规定,方案二和方案三经过对比分析可知,方案三误差更小,精度更高,因此针对精简后面积误差分析,方案三更可取。
(3)精简后测速垂线平均流速误差分析
根据计算成果表中数据,在方案一中,当累积频率为75%时所对应的相对误差绝对值介于7.56%~8.0%之间,超出误差范围,累积频率为 95%时,其相对误差绝对值介于11.76%~12.82%,也超出了规定范围,经计算,方案一不可取,舍弃方案一。在方案二中,当累积频率为75%时,其相对误差绝对值介于1.19%~2.56%之间,符合误差范围,当累积频率为95%时,其相对误差绝对值介于3.7%~17.95%之间[5]。在方案三中,当累积频率为75%时,其相对误差绝对值介于1.1%~1.28%之间,符合误差范围,当累积频率为95%时,其相对误差绝对值为3.48% 。方案一舍弃,方案二和方案三经过对比分析,方案三的误差较小。对于测速垂线平均流速的精简分析,方案三更加可取。
5 结论
本文以水文测验这门学科为基础,收集丹江水文站水位、降水、流量等相关资料,将精测流量、精测面积以及精测平均流速进行常测法精简分析,制定最佳方案能够近似代替 精测法,为丹江水文站今后的流量测验提供了思路和可行性建议,所得出的结论如下:
(1)丹江水文站2015年中水水位适用于常测法的精简分析。在精简分析中,测速垂线 越多,其相对误差绝对值越小,精度越高,越能够保持大断面形态和垂线流速分布形态。
(2)本次通过对丹江水文站测速垂线的精简分析,最终制定了方案三,即常测法保留12 条测速垂线的最佳方案,其河流特性及水情特征为其他丹江河测区提供了方法和理论依据。通过对丹江水文站中水水位的流量测验精简,为以后出现高水水位和低水水位时提供了精测思路和方法。
(3)常测法精简分析可以减少测速历时,节约人力财力,当出现紧急汛期,能够在短时间内完成流量测验,同时能够确保精度和可靠性,将水文资料和信息迅速提供给上级单位用于防洪减灾。

