常规布局低速固定翼无人机的参数辨识
杨爱斌,陈 诚,夏知胜
(沈阳航空航天大学 航空宇航学院,辽宁 沈阳)
随着21 世纪的发展,行业的需求,越来越多的中小型固定无人机被设计并制造出来。固定翼无人机的广泛使用,越来越需要识别其运动特征的飞行动力学模型,并且计算机技术不断进步使得模型辨识精度越来越高,在飞行器领域的应用越来越广泛[1],飞行器系统识别实现了基于模型的风险评估、控制系统设计、飞行器容错设计、飞行质量分析、飞行模拟以及未用于系统识别过程的计算或实验方法中获得结果的验证,用于表征全尺寸固定翼飞机的参数辨识方法已经得到了很好的发展[2,3],但相关方法并不直接适用于小型、低成本的无人机[4]。多数的军事和民用飞机都配备相关的系统辨识系统,但它们投入了大量的财力和物力,高精度的仪器为飞机的准确建模提供了高质量的数据;小型固定翼无人机通常配备质量较低的传感器,且更容易受到大气干扰,特别是在大气边界层内,这些因素降低了实验数据的质量,又反过来限制了参数辨识得到的模型质量[3]。尽管这些因素会导致参数辨识的难度,但因为其具有较高的灵活性和低风险性提供了更多的飞行可能,获取数据更加容易,在进行飞行数据的处理后,可用于参数辨识的过程[5]。
1 固定翼无人机动力学建模与解算
1.1 飞行器的基本参数
本文所仿真的固定翼飞行器为常规型布局,是一种小型固定翼无人机,机身总质量1 Kg,翼展为1.20 m。常规布局的固定翼具有结构简单、重量轻、飞行操作简单、便于维护等优点。根据XFLR5[6]相关文档的建议,定义了机翼、水平尾翼和垂直尾翼,省略了机身[7],这种简化不会影响最终结果的质量,但可以消除机身对于计算带来的困难,飞行器基本参数见表1。

表1 飞行器基本参数
1.2 固定翼飞机运动方程
刚性飞行器由于受到自身重力和空气动力,产生了飞行器的平动和转动运动。气动力(X Y Z)和力矩(L M N)通常以无量纲形式表示,如下:
飞机参数辨识的主要任务是得到这些气动力系数和力矩系数[2,3]。地球参考系定义为x y z 分别朝向北东地,机体参考系的原点为飞机的质心,x 轴穿过坐标原点指向机头,y 轴指向飞机右侧机翼,垂直x 轴,z 轴指向大地,遵循右手定则理论。欧拉角速率(φ ,θ,ψ)与机体角速率分量(p,q,r)联立的转动运动学方程为:
转动动力学方程为:
上述方程中,平动动力学和转动动力学的计算都依赖于两个气流角 α,β和飞行速度V,因此,将平动动力学方程组写成飞行速度V、迎角 α 和侧滑角β表示的形式更便于计算,因此有:
1.3 仿真模型的搭建
飞行器的模型主要包含空气动力学模型、飞行动力学模型、环境模型、飞行器信号输入模块、飞行器信号输出以及数据采集等模型。通过输入信号的激励,空气动力学模块求解出力和力矩,飞行动力学模块六自由度方程解析出飞行器的状态量,由传感器接收并收集,部分状态量通过反馈回路发送到空气动力学模块。
2 飞行器系统识别
2.1 激励输入设计
系统辨识是通过采集飞行器在实际飞行中或者仿真实验过程中输入和输出的实验数据,结合相关的参数辨识方法进行参数估计,为给定飞行器动力学系统建立数学模型的过程[8]。VLM 模型的模态分析如表2 所示,短周期模态和荷兰滚模态的结果直接用于控制输入的设计,在飞行仿真实验中没有考虑长周期模态,因为对于这种尺寸的飞机来说,它们的特征响应时间太长,不容易识别。

表2 VLM 模型的模态分析
为了确保输入的激励信号能够充分激发飞行器的动态模态,选择短周期和荷兰滚机动的输入时间步长为各自模态振荡周期的一半[2]。
2.2 运动一致性检查
在参数辨识过程之前,确定数据是否运动一致是至关重要的。运动一致性检查是对飞行器运动学进行积分,将测量到的平移加速度和角速度作为输入,得到飞行路径重建(FPR)结果,如果状态变量的积分结果与测量结果一致,则称飞行数据是运动学一致的。用式(14-19)计算机体速度、机体加速度和机体角速度的分量,气动力和力矩系数用式(1)计算。在检查运动学一致性时,由于运动学方程不是渐近稳定的,输出变量中有一些漂移是正常的[2]。
3 飞行器气动参数辨识
3.1 模型结构开发
气动模型通常取决于速度分量u、v、w(或者V、α、β)以及角速度分量p、q、r和控制舵面,并以多项式的形式表达,多项式中的系数表示因变量对状态变量变化的灵敏度。假设飞行器的横向和纵向是互相解耦的,这是基于对称性和经验推导出来的[9]。采用逐步回归方法,以多项式的形式确定气动力和气动力矩的模型结构。用来评估整体模型拟合程度的常见指标是决定系数R2,设y 为因变量(预报量),xi是自变量(预报因子),θi是待定参数,表示 θi的最小二乘估计,N 是数据总数点,有:
式中
在逐步回归方法中,分析模型项的指标是偏F 统计量F0和响应变量r 的偏相关系数。对于第i 个模型项,设表示单个参数估计,σi表示对应的标准误差,xi表示长度为N 的状态变量,表示其平均值,z 表示长度为N 的响应变量,z表示其平均值。对于第i 个模型项,有:
在模型结构中,F0值越大,表示项越重要。从模型结构中剔除的模型项,r 值接近于1,表明响应变量与潜在回归量之间存在显著关系[2]。
(1)纵向模型结构
采用短周期机动建立了纵向模型结构。纵向力和力矩系数Cx、Cz和Cm分别表示为纵向状态 α 、qˆ 与控制变量 δe的函数。确定Cx、Cz和Cm的模型结构为:
(2)横向模型结构
采用荷兰滚机动建立横向模型结构。横向力和力矩系数Cy、Cl和Cn分别表示为横向状态变量 β 、、和控制变量 δa、δr的函数。确定了Cy、Cl和Cn的模型结构:
3.2 参数辨识
飞机参数估计最常用的方法有输出误差法、方程误差法[2]。在塞斯纳citation2 飞机模型识别实验中,输出误差法和方程误差法都得到了类似的结果,结果表明,输出误差法比方程误差法具有更好的预测能力,但输出误差法计算速度较慢。方程误差法通常是基于最小二乘法则,将飞机实验数据计算出的气动力和力矩与数学模型预测的气动力和力矩的差最小化为准则。
最小二乘法参数估计公式如方程(31)所示。在此公式中,z(k)表示因变量,自变量为x1(k),x2(k),...,xn(k),因变量等于每个独立变量乘以对应的未知系数θ1,θ2,...,θn加误差项 ϵ (k),ϵ (k)如式(32)所示:
未知参数 θ是通过残差平方和最小求得。最小二乘代价函数J(θ)如式(33)所示,其中z 是包含所有z(k)的N×1维向量,X 是包含所有x1(k),x2(k),...,x n(k)的N×n矩阵。代价函数梯度如式(34)所示。由于方程误差是所有未知参数的线性函数,因此将代价函数的梯度置零可以最小化代价函数,从而得到式(35)。最后,利用式(36)得到未知参数的最小二乘估计 θ。
在残差相互独立的情况下,参数协方差矩阵P 如方程(37)所示,需要估计测量误差方差,如方程(38)所示。每个参数 θi估计的标准误差 σi是P 的相应对角线元素的平方根(方程(39))。个别参数估计 θi和θj之间的相关系数 ρij如方程(40)所示。
方程误差法状态变量可以是非线性的,但是要估计的参数必须与输出线性相关,这种方法计算效率非常高,即使在飞机不稳定的情况下,方程误差方法也是有效的,该方法还可以用于在同一数据集中将多个飞行操作同时进行估计参数。经辨识,气动导数估计值见表3。
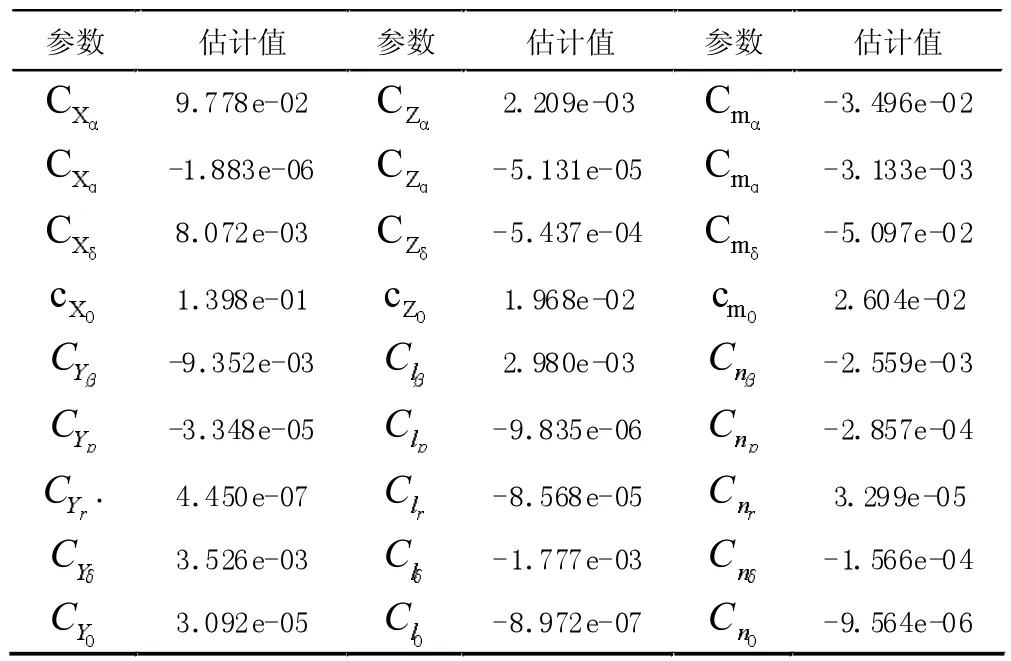
表3 飞行器纵向和横向气动导数估计值
3.3 参数辨识结果和模型验证
采用最小二乘回归方法实现了方程误差法。响应变量为飞机上的气动力和力矩,自变量由飞机相关状态和操纵面偏转组成。使用拟合优度(GOF)和泰尔不等式系数(TIC)[9]指标评估模型整体保真度。对于给定指标为i 的信号,由测量输出zi、预测输出yi和测量时间序列zi的初始值计算GOF:
GOF 值接近1 表示模型拟合良好。
当输出具有非零平均值时,TIC 可能会损坏,因此平均值被删除。TIC 的计算方法如下:
对于TIC,值为0 表示模型拟合完美; 数值低于0.25-0.3 表示建模性能良好[3]。计算所有验证机动的GOF 和TIC 指标,平均值如表4 和表5 所示。所有输出量的高GOF 值和低TIC 值表明具有良好的建模性能。

表4 纵向拟合优度和泰尔不等式系数值

表5 横向拟合优度和泰尔不等式系数值
4 结论
综上所述,小型、低成本、固定翼无人机可以较容易地获得有效的非线性飞行动力学模型。本文提出了初步模型假设、飞行实验设计、飞行仿真数据收集和处理、气动参数辨识和模型验证的相关方法,证实了所提出方法的有效性,同时作为一种工程方法,该气动参数辨识方法使用方便、计算速度快、精度良好。该方法不仅适用于本文研究的小型固定翼无人机,对多数的常规布局小型固定翼飞行器也是普遍适用的,在工程领域有着广泛的应用前景。

