计及模型差异的分布式电源优化配置方法研究

董 智，李小明，赵 阳

（国网河南省电力公司，河南郑州 450052）

随着“双碳”目标的确立，碳中和的概念改变了全社会用电需求的驱动力，风力发电、光伏发电等分布式发电技术的地位也愈发重要。与此同时，该技术也将得到迅速发展与大力推广。一方面，分布式发电技术具有良好的环境适应性及友好性；另一方面，自然条件严重限制了分布式发电的输出能力，导致其输出功率具有随机波动性，且在并网后会对电网的安全、稳定运行产生一定影响[1]。

分布式电源最大的特性便是分散性强、容量较小但数量多。其在现有分布式电源容量水平下，对电网的安全、稳定运行并未产生较大影响。但随着分布式发电技术的深入推广，一旦分布式电源的装机容量达到一定水平，必然会对电网保护性能的设定产生巨大影响。现阶段，分布式发电逆变输出直接并网于配网，即直接作用于配网，其电压波动及谐波占比严重影响了电网电能质量。

自然条件主导分布式电源的电压波动现象，只要分布式电源输出随机波动性电压，便会对电网的稳定性产生影响。此外，分布式电源的不同装机容量也会对电网产生不同程度的影响。因此，在某些情况下该电源输出的波动性电压将决定其装机容量。但若能优化光伏、风电等分布式电源的容量配置，进而找到分布式电源间的最优互补平衡，便可解决输出电压的随机波动性。分布式电源典型的结构特征是电子元件、换流器等元件占主导构架。与传统火力等发电相比，其开关元件的使用率更高，相应产生谐波也就越多，且还会使系统中谐波的产生机理及传输途径复杂且曲折，进而更易引发电压谐波占比率较高及稳定性较差的问题[2]。所以，研究如何消除分布式电源的输出电压波动性及谐波占比率具有重要意义。

为此，该文结合改进时间动态算法（Dynamic Time Warping，DTW）及遗传算法（Genetic Algorithm，GA）构建了最优化目标函数。在此基础上利用分布式优化技术进行求解，即考虑如何把一个综合性任务分解成若干子任务安排给多个核心，并利用这些核心来实现对一个总体问题的并行快速求解。通过遗传算法的目标线性函数进行最优搜索，并找寻系统的最佳接入点与注入容量，使得系统有功网损最小。最终，提供了可靠的分布式电源优化方案。

1 改进时间动态与遗传算法

对模拟信号m(t)与待测信号x(t)进行特征匹配计算，从相关系数算法的理论出发，可以将其理解为m(t)与x(t)的内积除以其模的乘积。而当x(t)分别为m(t)+Δ(t)和km(t)时，传统相关系数法与改进相关系数法处理的结果则有所不同[3]。对于信号m(t)和x(t)，传统相关系数c的计算公式为：

设Δ 为时间长度，当x(t)=m(t)+Δ 时，则有：

将上式离散化，有：

只有在Δ →0 时，α→0，相关系数c→1。

当x(t)=km(t)时，有：

此时，无论x(t)与m(t)的数值关系如何，相关系数c始终为1。所以当x(t)为m(t)的不同倍数时，无法识别传统的相关系数法，这就使基于相关系数算法的模板匹配方法所检测到的波形不具备唯一性。

该文改进的相关系数法对于信号m(t)和x(t)的计算公式定义为：

上式表明，当α→0，则有c→1 。即仅在Δ →0 时才会有c→1。

当x(t)=km(t)时，则：

为了综合平衡各参数在目标函数中的份额，考虑分布式电源的类型、安装位置及计划容量，通过设计可靠的目标函数，得到与实际运行状态相对应比例的目标函数，并用以权衡实际因素，且最终得到最优化的分布式电源配置布局[4-5]。

2 分布式电源属性分析

分布式电源发电效率及并网输出受限于自然条件，自然条件的不定性直接造成该电源的电压波动[7-8]。主流的分布式电源包括分布式光伏、双馈风电机组等发电技术。各自运行状态的差异性决定了输出功率的波动性，造成功率的波动性大致存在3种情况[9-10]：

1）自然条件造成原始随机性

分布式光伏发电装置如何确定最佳阳光角度，是决定发电效率及输出电压波动性的主导因素，而风电机组的输出功率则受风力角度及方向等因素主导。为了最大化分布式电源发电效率及最小化电压波动，例如光伏、风机等分布式能源发电采用动态跟随方式。然而自然条件的变化决定了动态跟随方式，因此其输出功率在不同时段会产生不同的波动[11]。

2）分布式电源启动、停运统一性较差

由于分散性强、容量较小等问题，大多数分布式电源不属于国家所有，因此较难做到分布式电源启动、停运统一性。而错过最佳启停时间则会极大影响电网的安全、稳定运行[12]。

3）内部转化效率及其他外界干扰

自然条件限制分布式能源的发电效率，内部电子元件固有效率则限制发电输出效率，因此高效、便捷的发电组合元件尤为重要。此外，还有其他一些外界干扰因素，如输电方式、调峰等。

以上内在及外在的不可抗力因素决定了分布式发电的输出效率，故优化分布式能源配置是最小化内因及外因影响的重要手段。因此，采用某种算法或改善硬件条件均能使复杂的分布式能源配置问题简单化，从而保障电网的安全、稳定。

3 混合数据处理算法

由于数据含有噪声，所以需先对数据进行噪声预处理，再基于改进时间动态算法实现对数据的时间性排列。最后再与遗传算法相结合，获取与实际对应的目标函数，并考虑类型、位置与容量因素。以此优化分布式电源配置，进而确定最优网损下的可靠运行方式[13]。

3.1 算法设计

噪声是实际数据采集中固有的异常数据，其特性区别于有效数据。而分布式电源监测电压的数据为正弦式分布，且在分辨数据时有高值、低值及零值噪声。但由于一定范围内的数据恒定不变，所以必须依靠相应剔除算法来获取有效数据，并用于分布式电源的最优化配置。例如对光伏并网数据进行检测，发现有58 条记录中有异常值，其可细分为3 种情况：

1）12 条记录，5 个字段值全为0，6 个字段值全为高值，1 个字段值则全为低值，可在噪声分析时剔除该类记录。

2）其中，1条记录中的零值为正常值，即恰好为0。

3）剩下记录的零值为异常值，可采用相邻两个值的平均值将其替换。

剔除异常数值的核心是设定有效值范围及相邻值的记忆，监测值若超过有效值范围则剔除，若低于相邻两侧区间值也应剔除。则最终正常范围内的剩余数据，即为有效值。分布式电源数据监测及数据的分类，如图1、2 所示。

图1 分布式电源数据监测

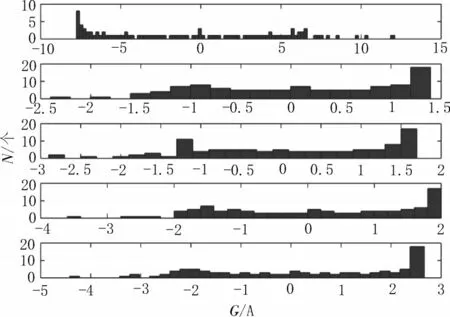
图2 分布式电源有效及异常数据分类

自然选择保留优良基因，进化获取适合的生存基因，遗传算法便是模拟自然优劣淘汰、适者生存的规则，通过多次迭代性遗传、变异、交叉与复制，来获得问题的最优解[14-15]。该文采用遗传算法的基本迭代思想，来解决分布式电源的优化配置的实际问题。

在遗传算法中，需解决映射问题，即“数学建模”，使用分散设定阈值范围判断[16-18]。首先将同类型分布式电源电气监测数据分批归类处理，统计不同位置电源的容量，以获取相应的电气监测数据，对监测数据x(t)与理论输出数据m(t)进行如上文所述的相关系数计算，得到数值c。最后，与设定阈值相比较，并结合位置、类型和容量等信息，再根据系数分布范围设定最优的电源分配。

3.2 仿真算例

为检验改进时间动态与遗传算法交叉模型的正确性，为光伏、风电等分布式电源电压的自适应控制、指导优化能源配置提供有力数据支撑。基于DIgSILENT 仿真平台搭建典型风机发电系统模型，不考虑系统故障，设定风机发电自然风速是10～14 m/s 的阶跃变化风速，检验模型的输出功率是否符合风机输出的电压特性。在不同风速下观察风机模型输出电压的波动性及随机性，同时基于混合算法观察电压及其他电气量的控制水平。运用IEEE14 节点系统模拟电力传输网络，如图3 所示，再对数据进行最优解寻找。

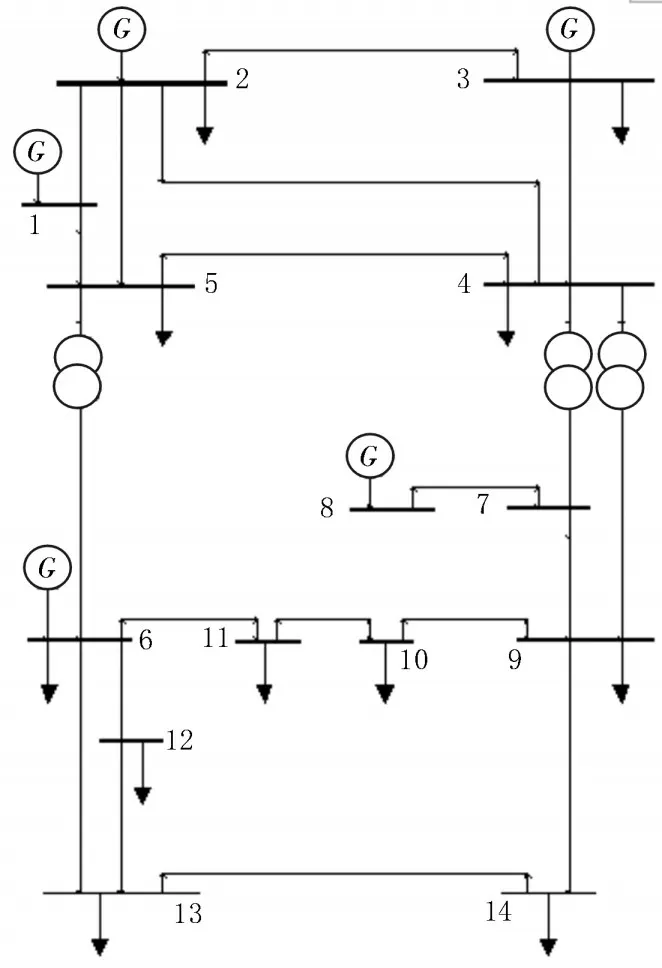
图3 IEEE14节点系统图

基于图3 所示的原始数据节点架构，采用算法结合方式搜寻最优目标函数，得到分布式电源优化后的最优解，从而根据实际位置、容量等因素配置分布式电源。

给风力发电系统提供10～14 m/s 变化的阶跃风速，分布式电源监测数据变化如图4 所示。

图4 分布式电源监测数据变化

不考虑任何外在或内在故障因素，在模型中按照风速设定方案添加风速因子，持续运行25 s。分布式电源输出的并网仿真数据如图5 所示。

图5 并网仿真数据1

改变风速因子，基于原方案继续运行25 s。分布式电源输出的仿真数据如图6 所示。

图6 并网仿真数据2

由上述分析结果可知，在实际的分布式电源优化配置中，安装位置是初始过程中的主导因素，其可决定光伏等分布式电源的发电效率，所以需要首先考虑位置的影响。而且改变风速因子后，输出量在一定波动周期后很快恢复稳定输出，表明提出方法的强自适应性。其次在位置确定后，再确定相应的安装容量。这样权衡分布式电源类型、位置与容量，并在此基础上利用最优目标函数，进一步取得最佳的配置适应度。由属性权重的最优分配获得环境成本及网损降低的最优方案，而最优配置方案的鲁棒性也更强。

4 结束语

该文提出了以分布式电源类型、位置和容量为目标函数建立基础因子，并采用改进时间动态算法和遗传算法优化了分布式电源配置。改进时间算法计算监测数据时间特性，结合遗传算法优胜劣汰的自然特性，且综合考虑了位置、容量及类型因素，解决了内在因素及外在干扰条件造成的分布式电源电压的输出问题，提高了能源配置的自适应及决策能力，从而达到了最优化配置分布式电源的目的，最终使能源配置效益提高15%。